2020—2021学年华东师大版九年级数学上册第23章图形的相似单元测试题(word解析版)
文档属性
| 名称 | 2020—2021学年华东师大版九年级数学上册第23章图形的相似单元测试题(word解析版) | 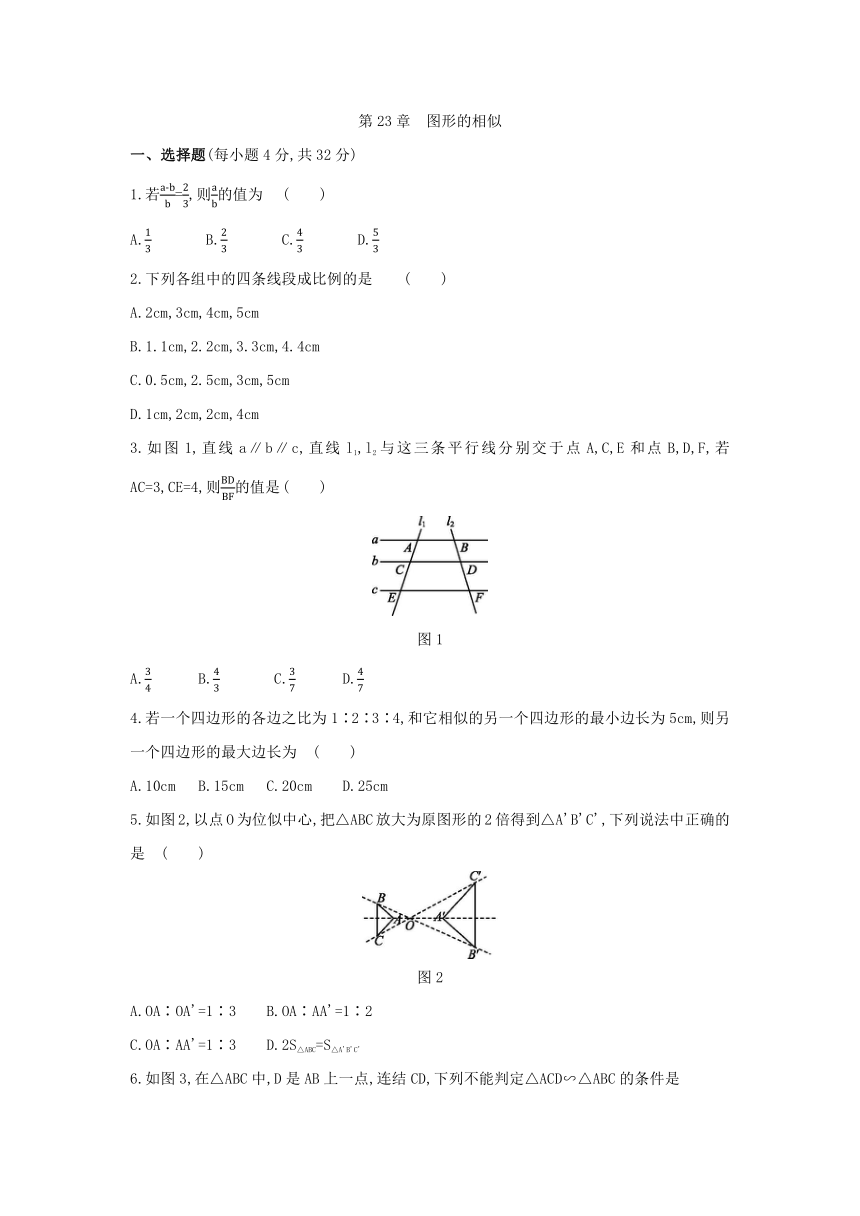 | |
| 格式 | zip | ||
| 文件大小 | 147.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-31 13:16:01 | ||
图片预览



文档简介
第23章 图形的相似
一、选择题(每小题4分,共32分)
1.若=,则的值为
( )
A.
B.
C.
D.
2.下列各组中的四条线段成比例的是
( )
A.2cm,3cm,4cm,5cm
B.1.1cm,2.2cm,3.3cm,4.4cm
C.0.5cm,2.5cm,3cm,5cm
D.1cm,2cm,2cm,4cm
3.如图1,直线a∥b∥c,直线l1,l2与这三条平行线分别交于点A,C,E和点B,D,F,若AC=3,CE=4,则的值是
( )
图1
A.
B.
C.
D.
4.若一个四边形的各边之比为1∶2∶3∶4,和它相似的另一个四边形的最小边长为5cm,则另一个四边形的最大边长为
( )
A.10cm
B.15cm
C.20cm
D.25cm
5.如图2,以点O为位似中心,把△ABC放大为原图形的2倍得到△A'B'C',下列说法中正确的是
( )
图2
A.OA∶OA'=1∶3
B.OA∶AA'=1∶2
C.OA∶AA'=1∶3
D.2S△ABC=S△A'B'C'
6.如图3,在△ABC中,D是AB上一点,连结CD,下列不能判定△ACD∽△ABC的条件是
( )
图3
A.∠ACD=∠B
B.∠ADC=∠ACB
C.=
D.AC2=AD·AB
7.如图4,线段CD两个端点的坐标分别为C(4,4),D(6,2),以原点O为位似中心,在第一象限内将线段CD缩小为原来的一半后得到线段AB,则端点A的坐标为
( )
图4
A.(2,2)
B.(3,3)
C.(3,1)
D.(4,1)
8.如图5,在△ABC中,中线BE,CD相交于点O,连结DE,有下列结论:①=;②=;③=;④=.其中正确的有
( )
图5
A.1个
B.2个
C.3个
D.4个
二、填空题(每小题5分,共30分)
9.已知△ABC∽△A'B'C',相似比为3∶4,△ABC的周长为6,则△A'B'C'的周长为 .?
10.如图6,D为△ABC外一点,AD与BC边的交点为E,AE=3,DE=5,BE=4,要使△BDE∽△ACE,那么线段CE的长应等于 .?
图6
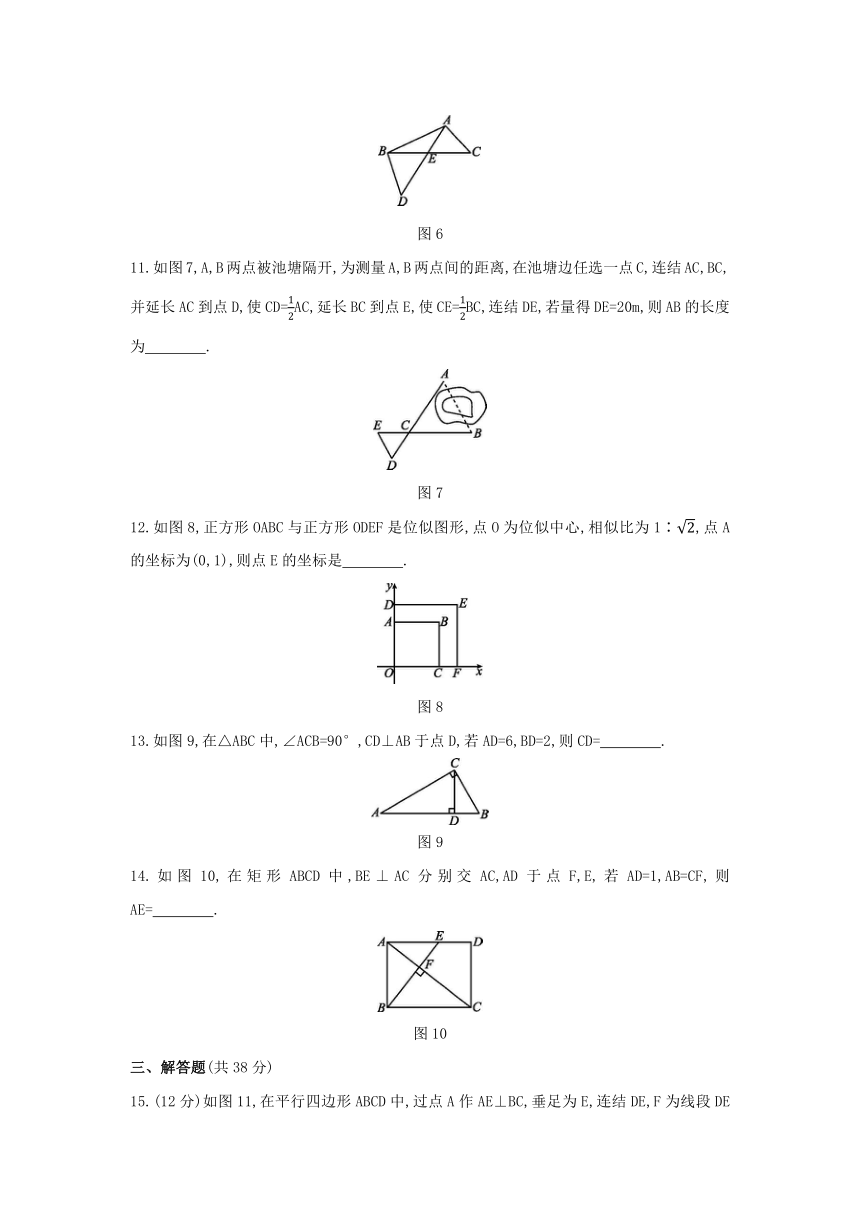
11.如图7,A,B两点被池塘隔开,为测量A,B两点间的距离,在池塘边任选一点C,连结AC,BC,并延长AC到点D,使CD=AC,延长BC到点E,使CE=BC,连结DE,若量得DE=20m,则AB的长度为 .?
图7
12.如图8,正方形OABC与正方形ODEF是位似图形,点O为位似中心,相似比为1∶,点A的坐标为(0,1),则点E的坐标是 .
图8
13.如图9,在△ABC中,∠ACB=90°,CD⊥AB于点D,若AD=6,BD=2,则CD= .?
图9
14.如图10,在矩形ABCD中,BE⊥AC分别交AC,AD于点F,E,若AD=1,AB=CF,则AE= .?
图10
三、解答题(共38分)
15.(12分)如图11,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连结DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:△ADF∽△DEC;
(2)若AB=6,AD=8,AF=4,求AE的长.
图11
16.(12分)如图12(示意图),小明为了测量底部不能到达的大树AB的高度,在离B点21米的N处放了一个平面镜,小明沿BN方向后退1.4米到D点,此时从镜子中恰好看到树顶的A点,已知小明的眼睛(点C)到地面的高度CD是1.6米,求大树AB的高度.
图12
17.(14分)提出问题
(1)如图13①所示,在等边三角形ABC中,M是BC上的任意一点(不含端点B,C),连结AM,以AM为边作等边三角形AMN,连结CN.求证:∠ABC=∠ACN.
类比探究
(2)如图②所示,在等边三角形ABC中,M是BC延长线上的任意一点(不含端点C),其他条件不变,(1)中结论∠ABC=∠ACN还成立吗?请说明理由.
拓展延伸
(3)如图③所示,在等腰三角形ABC中,BA=BC,M是BC上的任意一点(不含端点B,C),连结AM,以AM为边作等腰三角形AMN,使顶角∠AMN=∠ABC,连结CN.试探究∠ABC与∠ACN的数量关系,并说明理由.
①
② ③
图13
参考答案
1.[解析]D ∵=,∴5b=3a,∴=.
2.[解析]D A.2×5≠3×4,故四条线段不成比例;B.4.4×1.1≠3.3×2.2,故四条线段不成比例;C.0.5×5≠2.5×3,故四条线段不成比例;D.2×2=4×1,故四条线段成比例.
故选D.
3.[解析]C ∵a∥b∥c,∴==,∴==.故选C.
4.[解析]C 设它的最大边长为xcm.∵两个四边形相似,∴=,解得x=20.故选C.
5.C
6.[解析]C 因△ACD和△ABC已有一公共角,要使△ACD∽△ABC,则需再有一角对应相等,如∠ACD=∠B,∠ADC=∠ACB,故A,B正确;或公共角的两边对应成比例,如AD∶AC=AC∶AB,即AC2=AD·AB,故D正确,C错误.故选C.
7.[解析]A ∵以原点O为位似中心,在第一象限内将线段CD缩小为原来的一半后得到线段AB,点C的坐标为(4,4),∴点A的坐标为4×,4×,即(2,2).故选A.
8.C
9.[答案]8
[解析]∵△ABC∽△A'B'C',∴△ABC的周长∶△A'B'C'的周长=3∶4.∵△ABC的周长为6,∴△A'B'C'的周长=6×=8.
10.[答案]
[解析]∵∠AEC=∠BED,∴当=时,△BDE∽△ACE,即=,
∴CE=.
11.[答案]40m
[解析]∵CD=AC,CE=BC,∴==.又∵∠ACB=∠DCE,∴△ABC∽△DEC,∴==2.∵DE=20m,∴AB=40m.故答案为40m.
12.[答案](,)
[解析]
如图,连结OE.∵正方形OABC与正方形ODEF是位似图形,点O为位似中心,∴OE一定经过点B.又∵点A的坐标为(0,1),∴OA=1,∴由勾股定理可求得OB=.∵正方形OABC与正方形ODEF是位似图形,点O为位似中心,相似比为1∶,∴OB∶OE=1∶,即OE=2,∴由勾股定理,得DE=EF=,即点E的坐标是(,).
13.[答案]2
[解析]∵∠ACB=90°,∴∠DCB+∠ACD=90°.∵CD⊥AB,∴∠A+∠ACD=90°,∴∠A=∠DCB.又∵∠ADC=∠CDB=90°,∴△ADC∽△CDB,∴=,即=,解得CD=2.故答案为2.
14.[答案]
[解析]∵四边形ABCD是矩形,∴BC=AD=1,∠EAB=∠ABC=90°,∴∠ABE+∠CBF=90°.∵BE⊥AC,∴∠BFC=90°,∴∠FCB+∠CBF=90°,∴∠ABE=∠FCB.在△ABE和△FCB中,∠EAB=∠BFC=90°,AB=CF,∠ABE=∠FCB,
∴△ABE≌△FCB,∴AE=BF,BE=BC=1.∵BE⊥AC,∴∠BAF+∠ABF=90°.∵∠ABF+∠AEB=90°,∴∠BAF=∠AEB.又∵∠BAE=∠AFB,∴△ABE∽△FBA,∴=,即=,∴AE=AB2.在Rt△ABE中,BE=1,根据勾股定理,得AB2+AE2=BE2=1,∴AE+AE2=1.∵AE>0,∴AE=.
15.解:(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,AB=CD,
∴∠ADE=∠DEC,∠B+∠C=180°.
∵∠AFE=∠B,∠AFE+∠AFD=180°,
∴∠C=∠AFD,
∴△ADF∽△DEC.
(2)∵AB=6,∴CD=6.
∵△ADF∽△DEC,
∴=,
∴=,∴DE=12.
∵AE⊥BC,AD∥BC,∴AE⊥AD,
∴AE2=DE2-AD2=144-64=80,
∴AE=4.
16.解:∵AB⊥DB,CD⊥DB,
∴∠CDN=∠ABN=90°.
又∵∠CND=∠ANB,
∴△CDN∽△ABN,
∴=,即=,
∴AB=1.6×21÷1.4=24(米).
答:大树AB的高度为24米.
17.解:(1)证明:∵△ABC与△AMN均为等边三角形,
∴AB=AC,AM=AN,∠BAC=∠MAN=60°,
∴∠BAM=∠CAN,
∴△BAM≌△CAN(S.A.S.),
∴∠ABC=∠ACN.
(2)结论∠ABC=∠ACN仍成立.
理由:∵△ABC与△AMN均为等边三角形,
∴AB=AC,AM=AN,∠BAC=∠MAN=60°,
∴∠BAM=∠CAN,
∴△BAM≌△CAN,
∴∠ABC=∠ACN.
(3)∠ABC=∠ACN.
理由:∵BA=BC,MA=MN,∠ABC=∠AMN,
∴=,∠BAC=∠MAN,
∴△ABC∽△AMN,
∴=.
又∵∠BAM=∠BAC-∠MAC,∠CAN=∠MAN-∠MAC,
∴∠BAM=∠CAN,
∴△BAM∽△CAN,
∴∠ABC=∠ACN.
一、选择题(每小题4分,共32分)
1.若=,则的值为
( )
A.
B.
C.
D.
2.下列各组中的四条线段成比例的是
( )
A.2cm,3cm,4cm,5cm
B.1.1cm,2.2cm,3.3cm,4.4cm
C.0.5cm,2.5cm,3cm,5cm
D.1cm,2cm,2cm,4cm
3.如图1,直线a∥b∥c,直线l1,l2与这三条平行线分别交于点A,C,E和点B,D,F,若AC=3,CE=4,则的值是
( )
图1
A.
B.
C.
D.
4.若一个四边形的各边之比为1∶2∶3∶4,和它相似的另一个四边形的最小边长为5cm,则另一个四边形的最大边长为
( )
A.10cm
B.15cm
C.20cm
D.25cm
5.如图2,以点O为位似中心,把△ABC放大为原图形的2倍得到△A'B'C',下列说法中正确的是
( )
图2
A.OA∶OA'=1∶3
B.OA∶AA'=1∶2
C.OA∶AA'=1∶3
D.2S△ABC=S△A'B'C'
6.如图3,在△ABC中,D是AB上一点,连结CD,下列不能判定△ACD∽△ABC的条件是
( )
图3
A.∠ACD=∠B
B.∠ADC=∠ACB
C.=
D.AC2=AD·AB
7.如图4,线段CD两个端点的坐标分别为C(4,4),D(6,2),以原点O为位似中心,在第一象限内将线段CD缩小为原来的一半后得到线段AB,则端点A的坐标为
( )
图4
A.(2,2)
B.(3,3)
C.(3,1)
D.(4,1)
8.如图5,在△ABC中,中线BE,CD相交于点O,连结DE,有下列结论:①=;②=;③=;④=.其中正确的有
( )
图5
A.1个
B.2个
C.3个
D.4个
二、填空题(每小题5分,共30分)
9.已知△ABC∽△A'B'C',相似比为3∶4,△ABC的周长为6,则△A'B'C'的周长为 .?
10.如图6,D为△ABC外一点,AD与BC边的交点为E,AE=3,DE=5,BE=4,要使△BDE∽△ACE,那么线段CE的长应等于 .?
图6
11.如图7,A,B两点被池塘隔开,为测量A,B两点间的距离,在池塘边任选一点C,连结AC,BC,并延长AC到点D,使CD=AC,延长BC到点E,使CE=BC,连结DE,若量得DE=20m,则AB的长度为 .?
图7
12.如图8,正方形OABC与正方形ODEF是位似图形,点O为位似中心,相似比为1∶,点A的坐标为(0,1),则点E的坐标是 .
图8
13.如图9,在△ABC中,∠ACB=90°,CD⊥AB于点D,若AD=6,BD=2,则CD= .?
图9
14.如图10,在矩形ABCD中,BE⊥AC分别交AC,AD于点F,E,若AD=1,AB=CF,则AE= .?
图10
三、解答题(共38分)
15.(12分)如图11,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连结DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:△ADF∽△DEC;
(2)若AB=6,AD=8,AF=4,求AE的长.
图11
16.(12分)如图12(示意图),小明为了测量底部不能到达的大树AB的高度,在离B点21米的N处放了一个平面镜,小明沿BN方向后退1.4米到D点,此时从镜子中恰好看到树顶的A点,已知小明的眼睛(点C)到地面的高度CD是1.6米,求大树AB的高度.
图12
17.(14分)提出问题
(1)如图13①所示,在等边三角形ABC中,M是BC上的任意一点(不含端点B,C),连结AM,以AM为边作等边三角形AMN,连结CN.求证:∠ABC=∠ACN.
类比探究
(2)如图②所示,在等边三角形ABC中,M是BC延长线上的任意一点(不含端点C),其他条件不变,(1)中结论∠ABC=∠ACN还成立吗?请说明理由.
拓展延伸
(3)如图③所示,在等腰三角形ABC中,BA=BC,M是BC上的任意一点(不含端点B,C),连结AM,以AM为边作等腰三角形AMN,使顶角∠AMN=∠ABC,连结CN.试探究∠ABC与∠ACN的数量关系,并说明理由.
①
② ③
图13
参考答案
1.[解析]D ∵=,∴5b=3a,∴=.
2.[解析]D A.2×5≠3×4,故四条线段不成比例;B.4.4×1.1≠3.3×2.2,故四条线段不成比例;C.0.5×5≠2.5×3,故四条线段不成比例;D.2×2=4×1,故四条线段成比例.
故选D.
3.[解析]C ∵a∥b∥c,∴==,∴==.故选C.
4.[解析]C 设它的最大边长为xcm.∵两个四边形相似,∴=,解得x=20.故选C.
5.C
6.[解析]C 因△ACD和△ABC已有一公共角,要使△ACD∽△ABC,则需再有一角对应相等,如∠ACD=∠B,∠ADC=∠ACB,故A,B正确;或公共角的两边对应成比例,如AD∶AC=AC∶AB,即AC2=AD·AB,故D正确,C错误.故选C.
7.[解析]A ∵以原点O为位似中心,在第一象限内将线段CD缩小为原来的一半后得到线段AB,点C的坐标为(4,4),∴点A的坐标为4×,4×,即(2,2).故选A.
8.C
9.[答案]8
[解析]∵△ABC∽△A'B'C',∴△ABC的周长∶△A'B'C'的周长=3∶4.∵△ABC的周长为6,∴△A'B'C'的周长=6×=8.
10.[答案]
[解析]∵∠AEC=∠BED,∴当=时,△BDE∽△ACE,即=,
∴CE=.
11.[答案]40m
[解析]∵CD=AC,CE=BC,∴==.又∵∠ACB=∠DCE,∴△ABC∽△DEC,∴==2.∵DE=20m,∴AB=40m.故答案为40m.
12.[答案](,)
[解析]
如图,连结OE.∵正方形OABC与正方形ODEF是位似图形,点O为位似中心,∴OE一定经过点B.又∵点A的坐标为(0,1),∴OA=1,∴由勾股定理可求得OB=.∵正方形OABC与正方形ODEF是位似图形,点O为位似中心,相似比为1∶,∴OB∶OE=1∶,即OE=2,∴由勾股定理,得DE=EF=,即点E的坐标是(,).
13.[答案]2
[解析]∵∠ACB=90°,∴∠DCB+∠ACD=90°.∵CD⊥AB,∴∠A+∠ACD=90°,∴∠A=∠DCB.又∵∠ADC=∠CDB=90°,∴△ADC∽△CDB,∴=,即=,解得CD=2.故答案为2.
14.[答案]
[解析]∵四边形ABCD是矩形,∴BC=AD=1,∠EAB=∠ABC=90°,∴∠ABE+∠CBF=90°.∵BE⊥AC,∴∠BFC=90°,∴∠FCB+∠CBF=90°,∴∠ABE=∠FCB.在△ABE和△FCB中,∠EAB=∠BFC=90°,AB=CF,∠ABE=∠FCB,
∴△ABE≌△FCB,∴AE=BF,BE=BC=1.∵BE⊥AC,∴∠BAF+∠ABF=90°.∵∠ABF+∠AEB=90°,∴∠BAF=∠AEB.又∵∠BAE=∠AFB,∴△ABE∽△FBA,∴=,即=,∴AE=AB2.在Rt△ABE中,BE=1,根据勾股定理,得AB2+AE2=BE2=1,∴AE+AE2=1.∵AE>0,∴AE=.
15.解:(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,AB=CD,
∴∠ADE=∠DEC,∠B+∠C=180°.
∵∠AFE=∠B,∠AFE+∠AFD=180°,
∴∠C=∠AFD,
∴△ADF∽△DEC.
(2)∵AB=6,∴CD=6.
∵△ADF∽△DEC,
∴=,
∴=,∴DE=12.
∵AE⊥BC,AD∥BC,∴AE⊥AD,
∴AE2=DE2-AD2=144-64=80,
∴AE=4.
16.解:∵AB⊥DB,CD⊥DB,
∴∠CDN=∠ABN=90°.
又∵∠CND=∠ANB,
∴△CDN∽△ABN,
∴=,即=,
∴AB=1.6×21÷1.4=24(米).
答:大树AB的高度为24米.
17.解:(1)证明:∵△ABC与△AMN均为等边三角形,
∴AB=AC,AM=AN,∠BAC=∠MAN=60°,
∴∠BAM=∠CAN,
∴△BAM≌△CAN(S.A.S.),
∴∠ABC=∠ACN.
(2)结论∠ABC=∠ACN仍成立.
理由:∵△ABC与△AMN均为等边三角形,
∴AB=AC,AM=AN,∠BAC=∠MAN=60°,
∴∠BAM=∠CAN,
∴△BAM≌△CAN,
∴∠ABC=∠ACN.
(3)∠ABC=∠ACN.
理由:∵BA=BC,MA=MN,∠ABC=∠AMN,
∴=,∠BAC=∠MAN,
∴△ABC∽△AMN,
∴=.
又∵∠BAM=∠BAC-∠MAC,∠CAN=∠MAN-∠MAC,
∴∠BAM=∠CAN,
∴△BAM∽△CAN,
∴∠ABC=∠ACN.
