湘教版数学八年级上册2.4 线段的垂直平分线同步练习(word解析版)
文档属性
| 名称 | 湘教版数学八年级上册2.4 线段的垂直平分线同步练习(word解析版) |
|
|
| 格式 | zip | ||
| 文件大小 | 349.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-31 00:00:00 | ||
图片预览



文档简介
2.4
线段的垂直平分线
一、单选题
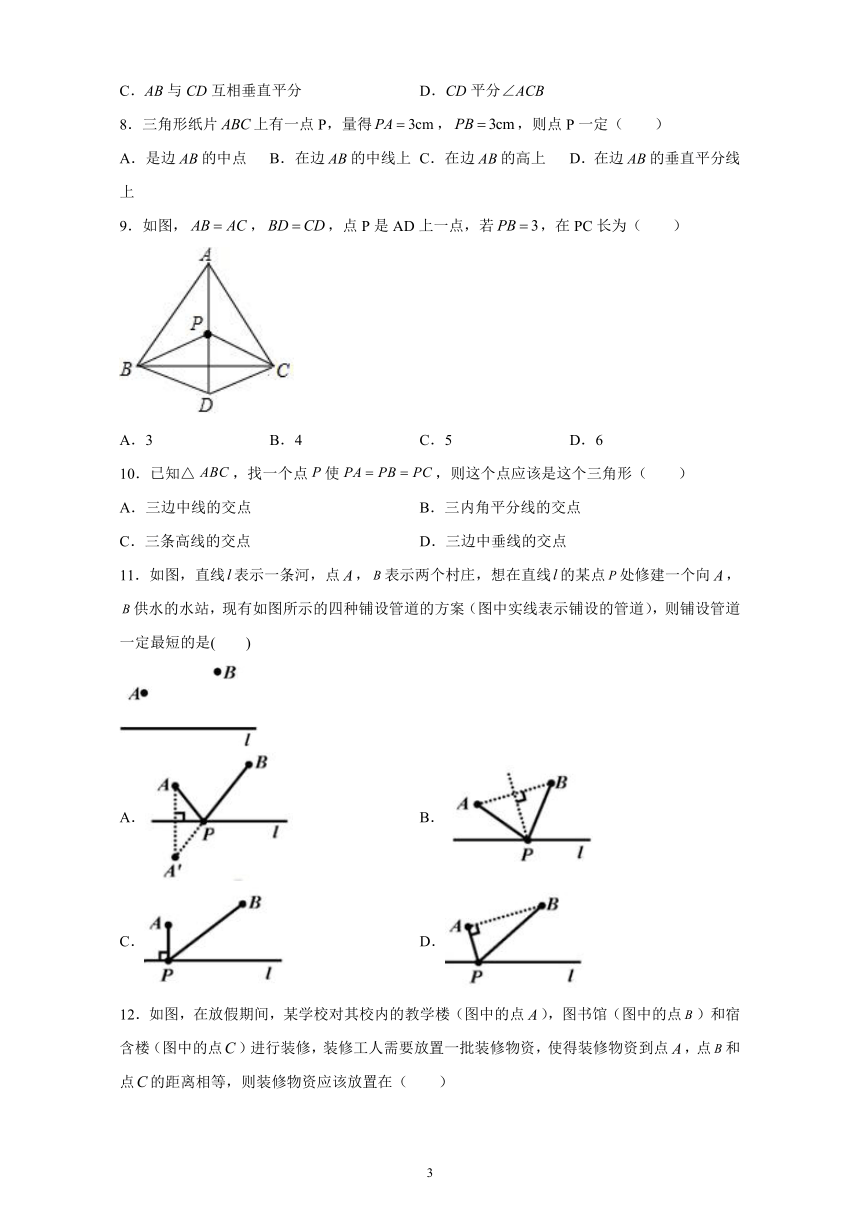
1.如图,已知线段,利用尺规作的垂直平分线,步骤如下:①分别以点为圆心,以的长为半径作弧,两弧相交于点和.②作直线.直线就是线段的垂直平分线.则的长可能是(
)
A.1
B.2
C.3
D.4
2.如图,在中,的垂直平分线分别交,于点,,若的周长为,,则的周长为(
)
A.
B.
C.
D.
3.如图,在中,,分别以点A,B为圆心,以大于的长为半径画弧,两弧交于D,E,经过D,E作直线分别交于点M,N,连接,下列结论正确的是(
)
A.
B.
C.
D.平分
4.如图,在△ABE中,∠E=25°,AE的垂直平分线MN交BE于点C,连接AC,若AB=AC,那么∠BAE的度数是(
)
A.100°
B.105°
C.110°
D.120°
5.如图,在△ABC中,∠B=30°,用直尺和圆规在边AB上确定一点D,则∠ADC=( )
A.30°
B.45°
C.50°
D.60°
6.如图,已知,直线与直线分别交于点,分别以点为圆心,大于的长为半径画弧,两弧相交于点,作直线,交直线b于点C,连接,若,则的度数是(
)
A.
B.
C.
D.
7.如图,AC=AD,BC=BD,则有( )
A.AB垂直平分CD
B.CD垂直平分AB
C.AB与CD互相垂直平分
D.CD平分∠ACB
8.三角形纸片上有一点P,量得,,则点P一定(
)
A.是边的中点
B.在边的中线上
C.在边的高上
D.在边的垂直平分线上
9.如图,,,点P是AD上一点,若,在PC长为(
)
A.3
B.4
C.5
D.6
10.已知△,找一个点使,则这个点应该是这个三角形(
)
A.三边中线的交点
B.三内角平分线的交点
C.三条高线的交点
D.三边中垂线的交点
11.如图,直线表示一条河,点,表示两个村庄,想在直线的某点处修建一个向,供水的水站,现有如图所示的四种铺设管道的方案(图中实线表示铺设的管道),则铺设管道一定最短的是(
)
B.
C.
D.
12.如图,在放假期间,某学校对其校内的教学楼(图中的点),图书馆(图中的点)和宿含楼(图中的点)进行装修,装修工人需要放置一批装修物资,使得装修物资到点,点和点的距离相等,则装修物资应该放置在(
)
A.、两边高线的交点处
B.在、两边中线的交点处
C.在、两内角平分线的交点处
D.在、两边垂直平分线的交点处
二、填空题
13.中垂线上的点到线段两端点的距离相等,请写出这个命题的逆命题:_____.
14.如图,△ABC中,AB=AC,DE是AB的垂直平分线,垂足为D,交AC于E,若AB=9cm,△BCE的周长为16cm,则BC=________cm.
15.如图,已知线段,其垂直平分线的作法如下:①分别以点和点为圆心,长为半径画弧,两弧相交于,两点;②作直线.上述作法中满足的条作为___1.(填“”,“”或“”)
16.如图,CD是AB的垂直平分线,若AC=1.6,BD=2.4,则四边形ACBD的周长为____.
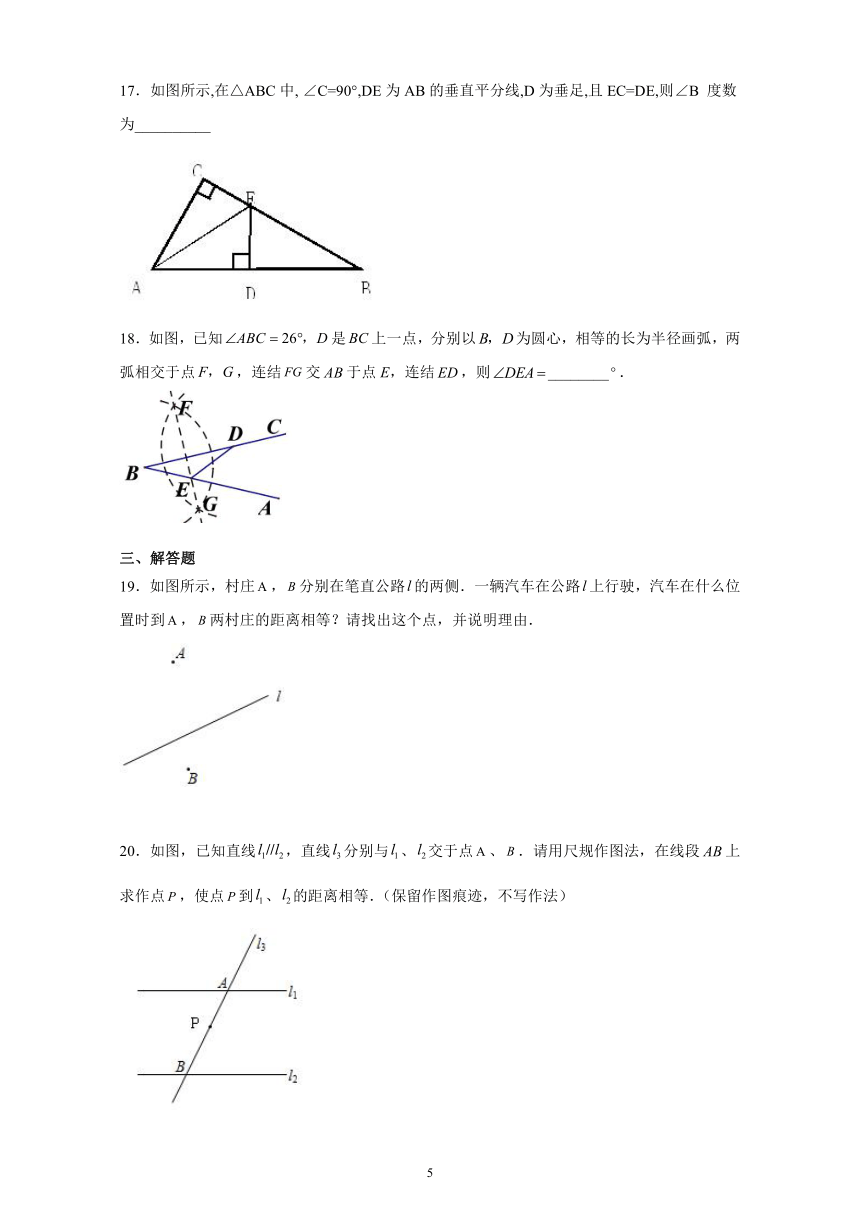
17.如图所示,在△ABC中,
∠C=90°,DE为AB的垂直平分线,D为垂足,且EC=DE,则∠B
度数为__________
18.如图,已知是上一点,分别以为圆心,相等的长为半径画弧,两弧相交于点,连结交于点E,连结,则________.
三、解答题
19.如图所示,村庄,分别在笔直公路的两侧.一辆汽车在公路上行驶,汽车在什么位置时到,两村庄的距离相等?请找出这个点,并说明理由.
20.如图,已知直线,直线分别与、交于点、.请用尺规作图法,在线段上求作点,使点到、的距离相等.(保留作图痕迹,不写作法)
21.如图,两条公路和相交于点,在的内部有工厂和,现要修建一个货站到两条公路,的距离相等,且到两工厂,的距离也相等,用尺规作出货站的位置.(要求:不写作法,保留作图痕迹,写出结论)
参考答案
1.D
解:根据题意得:b>AB,
即b>3,
故选:D.
2.B
解:∵DE为BC的垂直平分线,
∴,,
∵的周长为,,
∴,
∴的周长为,
故选:B.
3.B
解:由题意得:是线段的垂直平分线,
则,
故选:B.
4.B
解:∵MN是AE的垂直平分线,
∴CA=CE,
∴∠CAE=∠E=25°,
∴∠ACB=2∠E=50°,
∵AB=AC,
∴∠B=∠ACB=2∠E=50°,
∴∠BAC=180°-50°-50°=80°,
∴∠BAE=80°+25°=105°,
故选:B.
5.D
解:由图知虚线为的垂直平分线,
,
,
,
,
故选:D.
6.C
解:∵已知分别以点为圆心,大于的长为半径画弧,两弧相交于点,作直线,交直线b于点C,连接,
∴直线垂直平分线段AB,
∴,
∵,,
∴,
∴,
∴.
故选:C.
7.A
解:∵AC=AD,BC=BD,
∴点A在CD的垂直平分线上,点B在CD的垂直平分线上,
∴AB是CD的垂直平分线.
即AB垂直平分CD.
故选A
8.D
解:∵PA=3cm,PB=3cm
∴点P一定在边AB的垂直平分线上.
故选:D.
9.A
解:∵AB=AC,
BD=CD,
∴点A、D是BC垂直平分线上的点.
∵两点确定一条直线,
∴AD是BC的垂直平分线.
∴PC=PB.
∵PB=3,
∴PC=3.
故答案为:A.
10.D
解:∵PA=PB,
∴点P在AB的垂直平分线上,
∵PB=PC,
∴点P在BC的垂直平分线上,
∵PA=PC,
∴点P在AC的垂直平分线上,
∴点P是三角形三边垂直平分线即中垂线的交点.
故选:D
11.A
解:作点A关于直线l的对称点A′,连接BA′交直线l于P.
根据两点之间,线段最短,可知选项A铺设的管道最短.
故选:A.
12.D
解:作AC,BC两边的垂直平分线,它们的交点为P,由线段垂直平分线的性质,PA=PB=PC,
故选:D.
13.到线段两端点的距离相等的点在这条线段的中垂线上
解:中垂线上的点到线段两端点的距离相等,这个命题的逆命题是:到线段两端点的距离相等的点在这条线段的中垂线上.
故答案为:到线段两端点的距离相等的点在这条线段的中垂线上.
14.7
解:∵AB=9cm,
∴AC=AB=9cm,
∵DE是AB的垂直平分线,
∴AE=BE,
∴BE+CE=AE+CE=AC=AB=9cm,
∵△BCE的周长为16cm,
∴BC=16-9=7cm.
故答案为:7.
15.>
解:∵,
∴半径长度,
即.
故答案为:.
16.8
解:∵CD是AB的垂直平分线,
∴BC=AC=1.6,AD=BD=2.4,
∴四边形ACBD的周长为:AC+BC+BD+AD=8,
故答案为:8.
17.30°
解:∵EC=DE,∠C=90°,DE⊥AB,
∴∠CAE=∠DAE,
∵DE为AB的垂直平分线,
∴AE=BE,
∴∠B=∠DAE,
∴∠B=∠CAE=∠DAE,
在△ABC中,∠B+∠CAE+∠DAE=90°,
∴∠B=30°.
故答案为:30°.
18.
解:由题意得:垂直平分,
,
,
,
,
故答案为:.
19.位置见解析,理由见解析
解:如图,连接,作线段的垂直平分线,且交公路与点,点即为所求,
理由:∵点C是线段AB垂直平分线上的点,
∴CA=CB.
20.见解析
解:如图所示,点即为所求.
21.见解析
解:如图,作的平分线,的垂直平分线,与的交点就是货站的位置.
线段的垂直平分线
一、单选题
1.如图,已知线段,利用尺规作的垂直平分线,步骤如下:①分别以点为圆心,以的长为半径作弧,两弧相交于点和.②作直线.直线就是线段的垂直平分线.则的长可能是(
)
A.1
B.2
C.3
D.4
2.如图,在中,的垂直平分线分别交,于点,,若的周长为,,则的周长为(
)
A.
B.
C.
D.
3.如图,在中,,分别以点A,B为圆心,以大于的长为半径画弧,两弧交于D,E,经过D,E作直线分别交于点M,N,连接,下列结论正确的是(
)
A.
B.
C.
D.平分
4.如图,在△ABE中,∠E=25°,AE的垂直平分线MN交BE于点C,连接AC,若AB=AC,那么∠BAE的度数是(
)
A.100°
B.105°
C.110°
D.120°
5.如图,在△ABC中,∠B=30°,用直尺和圆规在边AB上确定一点D,则∠ADC=( )
A.30°
B.45°
C.50°
D.60°
6.如图,已知,直线与直线分别交于点,分别以点为圆心,大于的长为半径画弧,两弧相交于点,作直线,交直线b于点C,连接,若,则的度数是(
)
A.
B.
C.
D.
7.如图,AC=AD,BC=BD,则有( )
A.AB垂直平分CD
B.CD垂直平分AB
C.AB与CD互相垂直平分
D.CD平分∠ACB
8.三角形纸片上有一点P,量得,,则点P一定(
)
A.是边的中点
B.在边的中线上
C.在边的高上
D.在边的垂直平分线上
9.如图,,,点P是AD上一点,若,在PC长为(
)
A.3
B.4
C.5
D.6
10.已知△,找一个点使,则这个点应该是这个三角形(
)
A.三边中线的交点
B.三内角平分线的交点
C.三条高线的交点
D.三边中垂线的交点
11.如图,直线表示一条河,点,表示两个村庄,想在直线的某点处修建一个向,供水的水站,现有如图所示的四种铺设管道的方案(图中实线表示铺设的管道),则铺设管道一定最短的是(
)
B.
C.
D.
12.如图,在放假期间,某学校对其校内的教学楼(图中的点),图书馆(图中的点)和宿含楼(图中的点)进行装修,装修工人需要放置一批装修物资,使得装修物资到点,点和点的距离相等,则装修物资应该放置在(
)
A.、两边高线的交点处
B.在、两边中线的交点处
C.在、两内角平分线的交点处
D.在、两边垂直平分线的交点处
二、填空题
13.中垂线上的点到线段两端点的距离相等,请写出这个命题的逆命题:_____.
14.如图,△ABC中,AB=AC,DE是AB的垂直平分线,垂足为D,交AC于E,若AB=9cm,△BCE的周长为16cm,则BC=________cm.
15.如图,已知线段,其垂直平分线的作法如下:①分别以点和点为圆心,长为半径画弧,两弧相交于,两点;②作直线.上述作法中满足的条作为___1.(填“”,“”或“”)
16.如图,CD是AB的垂直平分线,若AC=1.6,BD=2.4,则四边形ACBD的周长为____.
17.如图所示,在△ABC中,
∠C=90°,DE为AB的垂直平分线,D为垂足,且EC=DE,则∠B
度数为__________
18.如图,已知是上一点,分别以为圆心,相等的长为半径画弧,两弧相交于点,连结交于点E,连结,则________.
三、解答题
19.如图所示,村庄,分别在笔直公路的两侧.一辆汽车在公路上行驶,汽车在什么位置时到,两村庄的距离相等?请找出这个点,并说明理由.
20.如图,已知直线,直线分别与、交于点、.请用尺规作图法,在线段上求作点,使点到、的距离相等.(保留作图痕迹,不写作法)
21.如图,两条公路和相交于点,在的内部有工厂和,现要修建一个货站到两条公路,的距离相等,且到两工厂,的距离也相等,用尺规作出货站的位置.(要求:不写作法,保留作图痕迹,写出结论)
参考答案
1.D
解:根据题意得:b>AB,
即b>3,
故选:D.
2.B
解:∵DE为BC的垂直平分线,
∴,,
∵的周长为,,
∴,
∴的周长为,
故选:B.
3.B
解:由题意得:是线段的垂直平分线,
则,
故选:B.
4.B
解:∵MN是AE的垂直平分线,
∴CA=CE,
∴∠CAE=∠E=25°,
∴∠ACB=2∠E=50°,
∵AB=AC,
∴∠B=∠ACB=2∠E=50°,
∴∠BAC=180°-50°-50°=80°,
∴∠BAE=80°+25°=105°,
故选:B.
5.D
解:由图知虚线为的垂直平分线,
,
,
,
,
故选:D.
6.C
解:∵已知分别以点为圆心,大于的长为半径画弧,两弧相交于点,作直线,交直线b于点C,连接,
∴直线垂直平分线段AB,
∴,
∵,,
∴,
∴,
∴.
故选:C.
7.A
解:∵AC=AD,BC=BD,
∴点A在CD的垂直平分线上,点B在CD的垂直平分线上,
∴AB是CD的垂直平分线.
即AB垂直平分CD.
故选A
8.D
解:∵PA=3cm,PB=3cm
∴点P一定在边AB的垂直平分线上.
故选:D.
9.A
解:∵AB=AC,
BD=CD,
∴点A、D是BC垂直平分线上的点.
∵两点确定一条直线,
∴AD是BC的垂直平分线.
∴PC=PB.
∵PB=3,
∴PC=3.
故答案为:A.
10.D
解:∵PA=PB,
∴点P在AB的垂直平分线上,
∵PB=PC,
∴点P在BC的垂直平分线上,
∵PA=PC,
∴点P在AC的垂直平分线上,
∴点P是三角形三边垂直平分线即中垂线的交点.
故选:D
11.A
解:作点A关于直线l的对称点A′,连接BA′交直线l于P.
根据两点之间,线段最短,可知选项A铺设的管道最短.
故选:A.
12.D
解:作AC,BC两边的垂直平分线,它们的交点为P,由线段垂直平分线的性质,PA=PB=PC,
故选:D.
13.到线段两端点的距离相等的点在这条线段的中垂线上
解:中垂线上的点到线段两端点的距离相等,这个命题的逆命题是:到线段两端点的距离相等的点在这条线段的中垂线上.
故答案为:到线段两端点的距离相等的点在这条线段的中垂线上.
14.7
解:∵AB=9cm,
∴AC=AB=9cm,
∵DE是AB的垂直平分线,
∴AE=BE,
∴BE+CE=AE+CE=AC=AB=9cm,
∵△BCE的周长为16cm,
∴BC=16-9=7cm.
故答案为:7.
15.>
解:∵,
∴半径长度,
即.
故答案为:.
16.8
解:∵CD是AB的垂直平分线,
∴BC=AC=1.6,AD=BD=2.4,
∴四边形ACBD的周长为:AC+BC+BD+AD=8,
故答案为:8.
17.30°
解:∵EC=DE,∠C=90°,DE⊥AB,
∴∠CAE=∠DAE,
∵DE为AB的垂直平分线,
∴AE=BE,
∴∠B=∠DAE,
∴∠B=∠CAE=∠DAE,
在△ABC中,∠B+∠CAE+∠DAE=90°,
∴∠B=30°.
故答案为:30°.
18.
解:由题意得:垂直平分,
,
,
,
,
故答案为:.
19.位置见解析,理由见解析
解:如图,连接,作线段的垂直平分线,且交公路与点,点即为所求,
理由:∵点C是线段AB垂直平分线上的点,
∴CA=CB.
20.见解析
解:如图所示,点即为所求.
21.见解析
解:如图,作的平分线,的垂直平分线,与的交点就是货站的位置.
同课章节目录
