2020—2021苏科版九年级数学上册第2章 对称图形——圆单元测试题(word解析版)
文档属性
| 名称 | 2020—2021苏科版九年级数学上册第2章 对称图形——圆单元测试题(word解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 258.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-31 15:34:02 | ||
图片预览


文档简介
第2章 对称图形——圆
一、选择题(每小题4分,共24分)
1.平面内有P,O两点,☉O的半径为5,若PO=4,则点P与☉O的位置关系是
( )
A.点P在☉O外
B.点P在☉O上
C.点P在☉O内
D.无法判断
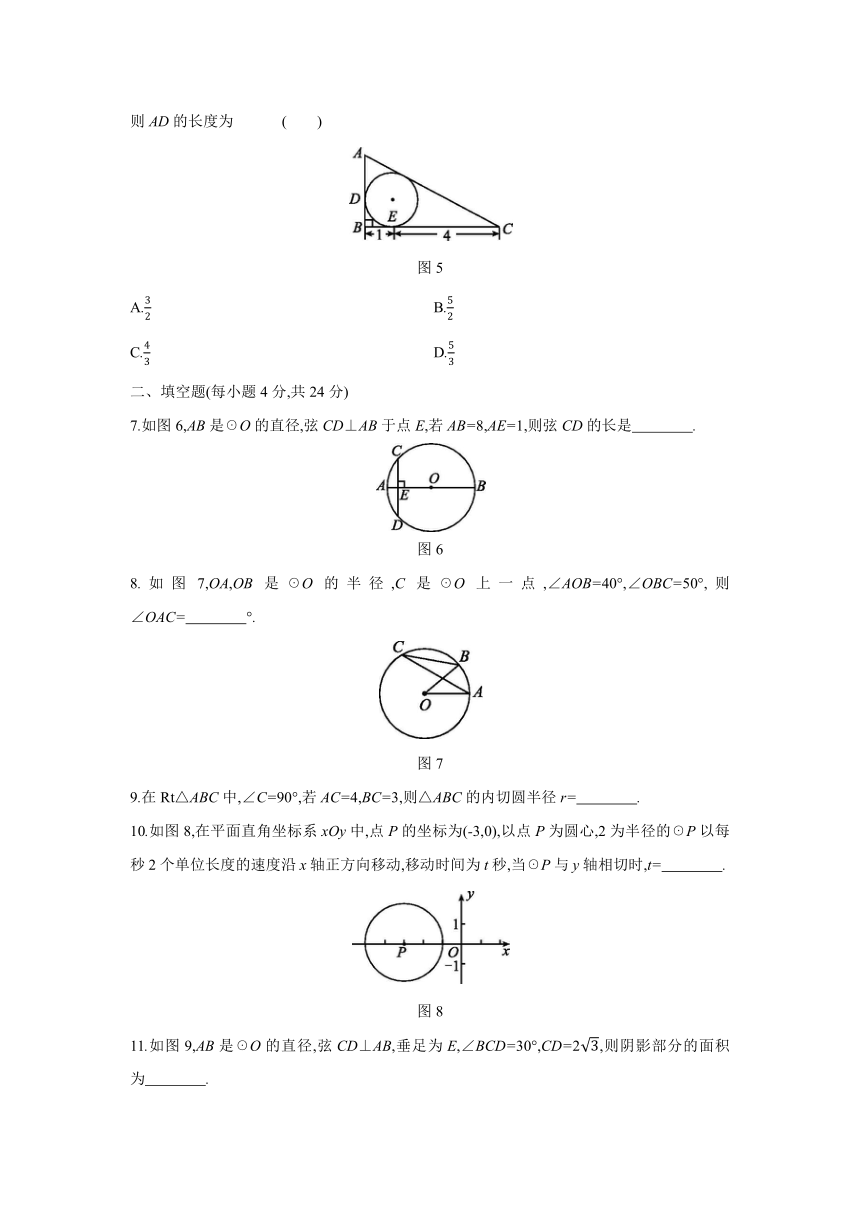
2.如图1,PA,PB分别与☉O相切于A,B两点,C为☉O上一点,连接AC,BC,若∠P=50°,则∠ACB的度数为
( )
图1
A.60°
B.75°
C.70°
D.65°
3.如图2,圆锥的底面圆半径r=6,高h=8,则圆锥的侧面积是
( )
图2
A.15π
B.30π
C.45π
D.60π
4.如图3,正六边形ABCDEF内接于☉O,连接BD,则∠CBD的度数是
( )
图3
A.30°
B.45°
C.60°
D.90°
5.如图4,四边形ABCD是菱形,☉O经过点A,C,D,与BC相交于点E,连接AC,AE.若∠D=80°,则∠EAC的度数为
( )
图4
A.20°
B.25°
C.30°
D.35°
6.如图5,直角三角形ABC的内切圆分别与AB,BC相切于点D,E,根据图中标示的长度与角度,则AD的长度为
( )
图5
A.
B.
C.
D.
二、填空题(每小题4分,共24分)
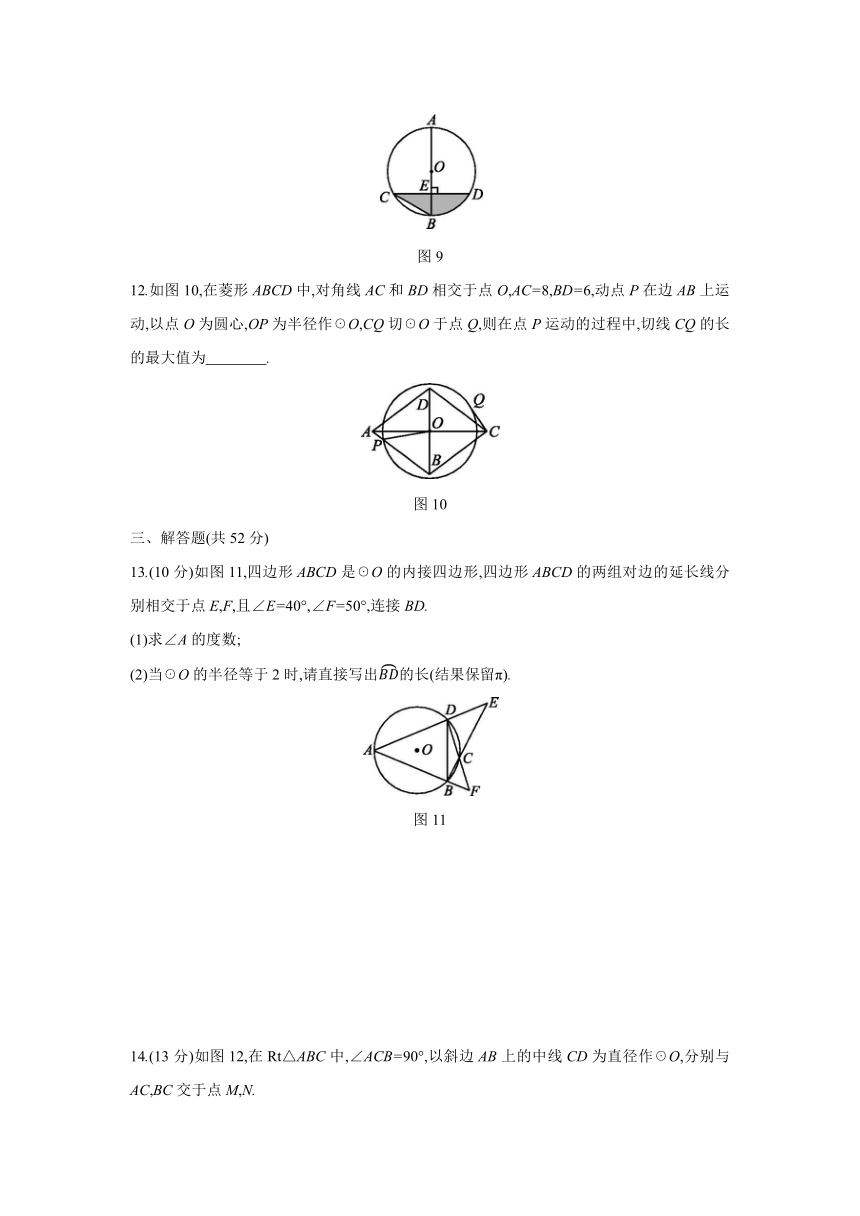
7.如图6,AB是☉O的直径,弦CD⊥AB于点E,若AB=8,AE=1,则弦CD的长是 .?
图6
8.如图7,OA,OB是☉O的半径,C是☉O上一点,∠AOB=40°,∠OBC=50°,则∠OAC= °.?
图7
9.在Rt△ABC中,∠C=90°,若AC=4,BC=3,则△ABC的内切圆半径r= .?
10.如图8,在平面直角坐标系xOy中,点P的坐标为(-3,0),以点P为圆心,2为半径的☉P以每秒2个单位长度的速度沿x轴正方向移动,移动时间为t秒,当☉P与y轴相切时,t= .?
图8
11.如图9,AB是☉O的直径,弦CD⊥AB,垂足为E,∠BCD=30°,CD=2,则阴影部分的面积为 .?
图9
12.如图10,在菱形ABCD中,对角线AC和BD相交于点O,AC=8,BD=6,动点P在边AB上运动,以点O为圆心,OP为半径作☉O,CQ切☉O于点Q,则在点P运动的过程中,切线CQ的长的最大值为 .?
图10
三、解答题(共52分)
13.(10分)如图11,四边形ABCD是☉O的内接四边形,四边形ABCD的两组对边的延长线分别相交于点E,F,且∠E=40°,∠F=50°,连接BD.
(1)求∠A的度数;
(2)当☉O的半径等于2时,请直接写出的长(结果保留π).
图11
14.(13分)如图12,在Rt△ABC中,∠ACB=90°,以斜边AB上的中线CD为直径作☉O,分别与AC,BC交于点M,N.
(1)过点N作☉O的切线NE与AB相交于点E,求证:NE⊥AB;
(2)连接MD,求证:MD=NB.
图12
15.(14分)如图13,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,点O在AB上,以点O为圆心,OA的长为半径的圆恰好经过点D,分别交AC,AB于点E,F.
(1)试判断直线BC与☉O的位置关系,并说明理由;
(2)若BD=2,BF=2,求☉O的半径.
图13
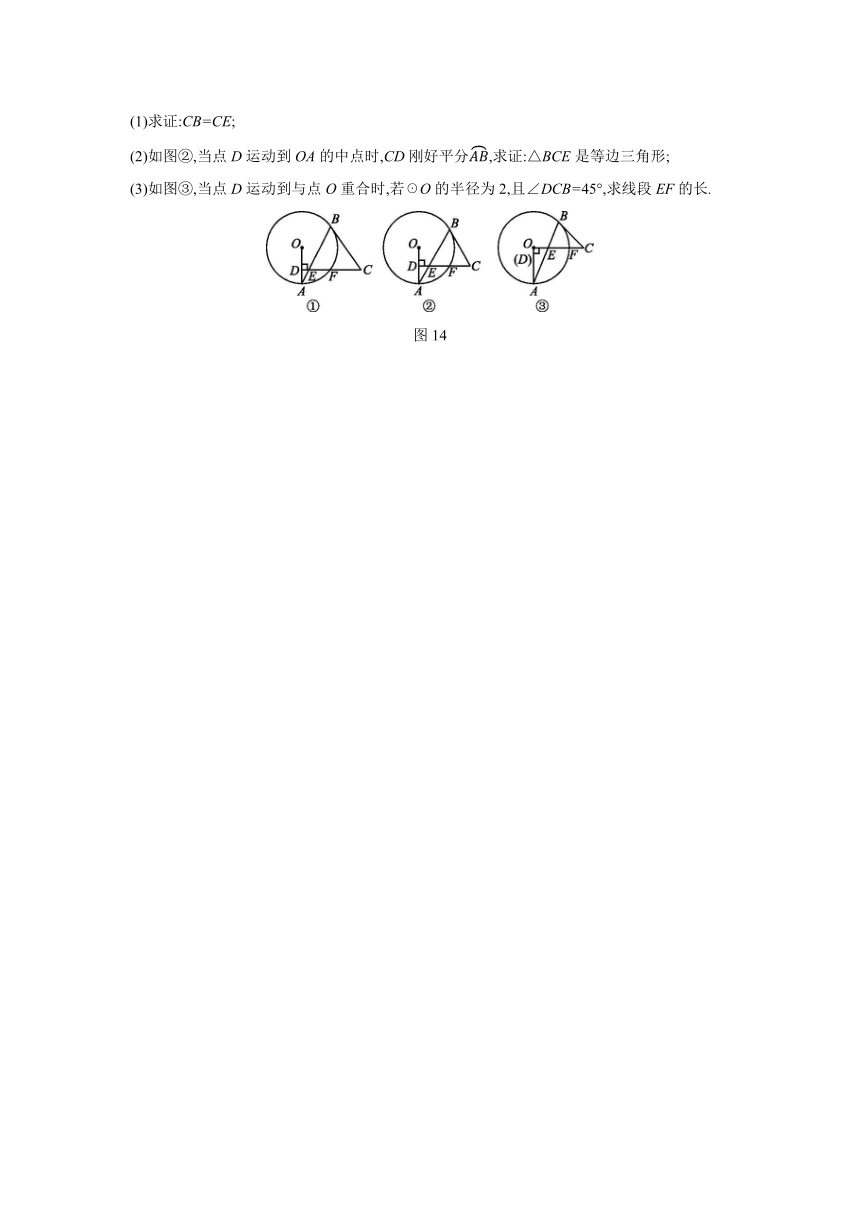
16.(15分)如图14①所示,OA是☉O的半径,D为OA上的一个动点,过点D作线段CD⊥OA交☉O于点F,过点C作☉O的切线BC,B为切点,连接AB,交CD于点E.
(1)求证:CB=CE;
(2)如图②,当点D运动到OA的中点时,CD刚好平分,求证:△BCE是等边三角形;
(3)如图③,当点D运动到与点O重合时,若☉O的半径为2,且∠DCB=45°,求线段EF的长.
图14
答案
1.[解析]
C ∵☉O的半径为5,PO=4,
∴4<5,
∴点P与☉O的位置关系是点P在☉O内.
故选C.
2.[解析]
D 连接OA,OB.
∵PA,PB分别与☉O相切于A,B两点,
∴OA⊥PA,OB⊥PB,
∴∠OAP=∠OBP=90°,
∴∠AOB=180°-∠P=180°-50°=130°,
∴∠ACB=∠AOB=×130°=65°.
故选D.
3.[解析]
D 圆锥的母线l===10,∴圆锥的侧面积=π×10×6=60π.故选D.
4.[解析]
A ∵在正六边形ABCDEF中,∠BCD==120°,BC=CD,∴∠CBD=(180°-120°)=30°.故选A.
5.[解析]
C ∵四边形ABCD是菱形,∠D=80°,
∴∠ACB=∠DCB=(180°-∠D)=50°.
∵四边形AECD是圆内接四边形,
∴∠AEB=∠D=80°,
∴∠EAC=∠AEB-∠ACB=30°.故选C.
6.[解析]
D 设AD=x.
∵直角三角形ABC的内切圆分别与AB,BC相切于点D,E,∴BD=BE=1,
∴AB=x+1,AC=AD+CE=x+4.
在Rt△ABC中,由勾股定理得(x+1)2+52=(x+4)2,解得x=,即AD的长度为.
故选D.
7.[答案]
2
[解析]
连接OC,如图.由题意,得OE=OA-AE=4-1=3,∴CE=ED==,∴CD=2CE=2.
8.[答案]
30
[解析]
如图,连接OC.
∵OC=OB,
∴∠OCB=∠OBC=50°,
∴∠BOC=180°-50°×2=80°,
∴∠AOC=80°+40°=120°.
∵OC=OA,
∴∠OAC=∠OCA=30°.故答案为30.
9.[答案]
1
[解析]
如图,设△ABC的内切圆与各边分别相切于点D,E,F,连接OD,OE,OF,
则OE⊥BC,OF⊥AB,OD⊥AC.
设☉O的半径为r,
∴CD=CE=r.
∵∠C=90°,AC=4,BC=3,
∴AB=5,
∴BE=BF=3-r,AF=AD=4-r,
∴4-r+3-r=5,
∴r=1,
∴△ABC的内切圆的半径为1.
10.[答案]
或
[解析]
当☉P位于y轴的左侧且与y轴相切时,平移的距离为1,t=1÷2=(秒);
当☉P位于y轴的右侧且与y轴相切时,平移的距离为5,t=5÷2=(秒).
故答案为或.
11.
12.[答案]
[解析]
如图,连接OQ.
∵CQ切☉O于点Q,∴OQ⊥CQ,
∴∠CQO=90°,
∴CQ=.
∵四边形ABCD是菱形,
∴AC⊥BD,OA=OC=AC=×8=4,OB=BD=×6=3,
∴AB==5.
∵OC是定值,则当OQ最小时,CQ最大,
即OP最小时,CQ最大,
∴当OP⊥AB时,CQ最大,此时OQ=OP==,∴CQ==.
故答案为.
13.解:(1)∵四边形ABCD是☉O的内接四边形,
∴∠DCE=∠A.
∵∠EDF=∠A+∠F=∠A+50°,
∠EDF+∠DCE+∠E=180°,
∴∠A+50°+∠A+40°=180°,
∴∠A=45°.
(2)连接OB,OD,如图.
∵∠BOD=2∠A=90°,
∴的长为=π.
14.证明:(1)连接ON,如图.
∵CD为斜边AB上的中线,
∴CD=AD=DB,
∴∠1=∠B.
∵OC=ON,
∴∠1=∠2,
∴∠2=∠B,∴ON∥DB.
∵NE为☉O的切线,
∴ON⊥NE,∴NE⊥AB.
(2)连接DN,如图.
∵CD为☉O的直径,
∴∠CMD=∠CND=90°.
又∵∠MCB=90°,
∴四边形CMDN为矩形,
∴MD=CN.
∵CD=DB,DN⊥BC,
∴CN=NB,∴MD=NB.
15.解:(1)直线BC与☉O相切.
理由:如图,连接OD.
∵OA=OD,∴∠OAD=∠ODA.
∵AD平分∠BAC,∴∠OAD=∠CAD,
∴∠ODA=∠CAD,
∴OD∥AC,∴∠C=∠ODB.
∵∠C=90°,
∴∠ODB=90°,即OD⊥BC.
∵OD为☉O的半径,
∴直线BC与☉O相切.
(2)设☉O的半径为R,
则OD=OF=R.
在Rt△BDO中,
由勾股定理,得OB2=BD2+OD2,
即(R+2)2=(2)2+R2,解得R=4,
即☉O的半径是4.
16.解:(1)证明:如图①,连接OB.
∵CB为☉O的切线,切点为B,
∴OB⊥BC,
∴∠OBC=90°,
∴∠OBA+∠CBE=90°.∵OA=OB,
∴∠DAE=∠OBA.
∵CD⊥OA,
∴∠DAE+∠DEA=90°,
∴∠DEA=∠CBE.
又∵∠CEB=∠DEA,
∴∠CEB=∠CBE,∴CB=CE.
(2)证明:如图②,连接OF,OB.
在Rt△ODF中,OF=OA=2OD,
∴∠OFD=30°,∴∠DOF=60°.
∵CD平分,
∴∠AOB=2∠AOF=120°,
∴∠C=360°-∠ODC-∠OBC-∠AOB=60°.
又∵CB=CE,
∴△BCE是等边三角形.
(3)如图③,连接OB,
∵BC是☉O的切线,
∴∠OBC=90°.
又∵∠DCB=45°,
∴△OBC为等腰直角三角形,
∴BC=OB=2,OC=2.
又∵CB=CE,
∴OE=OC-CE=OC-CB=2-2,
∴EF=DF-OE=2-(2-2)=4-2.
一、选择题(每小题4分,共24分)
1.平面内有P,O两点,☉O的半径为5,若PO=4,则点P与☉O的位置关系是
( )
A.点P在☉O外
B.点P在☉O上
C.点P在☉O内
D.无法判断
2.如图1,PA,PB分别与☉O相切于A,B两点,C为☉O上一点,连接AC,BC,若∠P=50°,则∠ACB的度数为
( )
图1
A.60°
B.75°
C.70°
D.65°
3.如图2,圆锥的底面圆半径r=6,高h=8,则圆锥的侧面积是
( )
图2
A.15π
B.30π
C.45π
D.60π
4.如图3,正六边形ABCDEF内接于☉O,连接BD,则∠CBD的度数是
( )
图3
A.30°
B.45°
C.60°
D.90°
5.如图4,四边形ABCD是菱形,☉O经过点A,C,D,与BC相交于点E,连接AC,AE.若∠D=80°,则∠EAC的度数为
( )
图4
A.20°
B.25°
C.30°
D.35°
6.如图5,直角三角形ABC的内切圆分别与AB,BC相切于点D,E,根据图中标示的长度与角度,则AD的长度为
( )
图5
A.
B.
C.
D.
二、填空题(每小题4分,共24分)
7.如图6,AB是☉O的直径,弦CD⊥AB于点E,若AB=8,AE=1,则弦CD的长是 .?
图6
8.如图7,OA,OB是☉O的半径,C是☉O上一点,∠AOB=40°,∠OBC=50°,则∠OAC= °.?
图7
9.在Rt△ABC中,∠C=90°,若AC=4,BC=3,则△ABC的内切圆半径r= .?
10.如图8,在平面直角坐标系xOy中,点P的坐标为(-3,0),以点P为圆心,2为半径的☉P以每秒2个单位长度的速度沿x轴正方向移动,移动时间为t秒,当☉P与y轴相切时,t= .?
图8
11.如图9,AB是☉O的直径,弦CD⊥AB,垂足为E,∠BCD=30°,CD=2,则阴影部分的面积为 .?
图9
12.如图10,在菱形ABCD中,对角线AC和BD相交于点O,AC=8,BD=6,动点P在边AB上运动,以点O为圆心,OP为半径作☉O,CQ切☉O于点Q,则在点P运动的过程中,切线CQ的长的最大值为 .?
图10
三、解答题(共52分)
13.(10分)如图11,四边形ABCD是☉O的内接四边形,四边形ABCD的两组对边的延长线分别相交于点E,F,且∠E=40°,∠F=50°,连接BD.
(1)求∠A的度数;
(2)当☉O的半径等于2时,请直接写出的长(结果保留π).
图11
14.(13分)如图12,在Rt△ABC中,∠ACB=90°,以斜边AB上的中线CD为直径作☉O,分别与AC,BC交于点M,N.
(1)过点N作☉O的切线NE与AB相交于点E,求证:NE⊥AB;
(2)连接MD,求证:MD=NB.
图12
15.(14分)如图13,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,点O在AB上,以点O为圆心,OA的长为半径的圆恰好经过点D,分别交AC,AB于点E,F.
(1)试判断直线BC与☉O的位置关系,并说明理由;
(2)若BD=2,BF=2,求☉O的半径.
图13
16.(15分)如图14①所示,OA是☉O的半径,D为OA上的一个动点,过点D作线段CD⊥OA交☉O于点F,过点C作☉O的切线BC,B为切点,连接AB,交CD于点E.
(1)求证:CB=CE;
(2)如图②,当点D运动到OA的中点时,CD刚好平分,求证:△BCE是等边三角形;
(3)如图③,当点D运动到与点O重合时,若☉O的半径为2,且∠DCB=45°,求线段EF的长.
图14
答案
1.[解析]
C ∵☉O的半径为5,PO=4,
∴4<5,
∴点P与☉O的位置关系是点P在☉O内.
故选C.
2.[解析]
D 连接OA,OB.
∵PA,PB分别与☉O相切于A,B两点,
∴OA⊥PA,OB⊥PB,
∴∠OAP=∠OBP=90°,
∴∠AOB=180°-∠P=180°-50°=130°,
∴∠ACB=∠AOB=×130°=65°.
故选D.
3.[解析]
D 圆锥的母线l===10,∴圆锥的侧面积=π×10×6=60π.故选D.
4.[解析]
A ∵在正六边形ABCDEF中,∠BCD==120°,BC=CD,∴∠CBD=(180°-120°)=30°.故选A.
5.[解析]
C ∵四边形ABCD是菱形,∠D=80°,
∴∠ACB=∠DCB=(180°-∠D)=50°.
∵四边形AECD是圆内接四边形,
∴∠AEB=∠D=80°,
∴∠EAC=∠AEB-∠ACB=30°.故选C.
6.[解析]
D 设AD=x.
∵直角三角形ABC的内切圆分别与AB,BC相切于点D,E,∴BD=BE=1,
∴AB=x+1,AC=AD+CE=x+4.
在Rt△ABC中,由勾股定理得(x+1)2+52=(x+4)2,解得x=,即AD的长度为.
故选D.
7.[答案]
2
[解析]
连接OC,如图.由题意,得OE=OA-AE=4-1=3,∴CE=ED==,∴CD=2CE=2.
8.[答案]
30
[解析]
如图,连接OC.
∵OC=OB,
∴∠OCB=∠OBC=50°,
∴∠BOC=180°-50°×2=80°,
∴∠AOC=80°+40°=120°.
∵OC=OA,
∴∠OAC=∠OCA=30°.故答案为30.
9.[答案]
1
[解析]
如图,设△ABC的内切圆与各边分别相切于点D,E,F,连接OD,OE,OF,
则OE⊥BC,OF⊥AB,OD⊥AC.
设☉O的半径为r,
∴CD=CE=r.
∵∠C=90°,AC=4,BC=3,
∴AB=5,
∴BE=BF=3-r,AF=AD=4-r,
∴4-r+3-r=5,
∴r=1,
∴△ABC的内切圆的半径为1.
10.[答案]
或
[解析]
当☉P位于y轴的左侧且与y轴相切时,平移的距离为1,t=1÷2=(秒);
当☉P位于y轴的右侧且与y轴相切时,平移的距离为5,t=5÷2=(秒).
故答案为或.
11.
12.[答案]
[解析]
如图,连接OQ.
∵CQ切☉O于点Q,∴OQ⊥CQ,
∴∠CQO=90°,
∴CQ=.
∵四边形ABCD是菱形,
∴AC⊥BD,OA=OC=AC=×8=4,OB=BD=×6=3,
∴AB==5.
∵OC是定值,则当OQ最小时,CQ最大,
即OP最小时,CQ最大,
∴当OP⊥AB时,CQ最大,此时OQ=OP==,∴CQ==.
故答案为.
13.解:(1)∵四边形ABCD是☉O的内接四边形,
∴∠DCE=∠A.
∵∠EDF=∠A+∠F=∠A+50°,
∠EDF+∠DCE+∠E=180°,
∴∠A+50°+∠A+40°=180°,
∴∠A=45°.
(2)连接OB,OD,如图.
∵∠BOD=2∠A=90°,
∴的长为=π.
14.证明:(1)连接ON,如图.
∵CD为斜边AB上的中线,
∴CD=AD=DB,
∴∠1=∠B.
∵OC=ON,
∴∠1=∠2,
∴∠2=∠B,∴ON∥DB.
∵NE为☉O的切线,
∴ON⊥NE,∴NE⊥AB.
(2)连接DN,如图.
∵CD为☉O的直径,
∴∠CMD=∠CND=90°.
又∵∠MCB=90°,
∴四边形CMDN为矩形,
∴MD=CN.
∵CD=DB,DN⊥BC,
∴CN=NB,∴MD=NB.
15.解:(1)直线BC与☉O相切.
理由:如图,连接OD.
∵OA=OD,∴∠OAD=∠ODA.
∵AD平分∠BAC,∴∠OAD=∠CAD,
∴∠ODA=∠CAD,
∴OD∥AC,∴∠C=∠ODB.
∵∠C=90°,
∴∠ODB=90°,即OD⊥BC.
∵OD为☉O的半径,
∴直线BC与☉O相切.
(2)设☉O的半径为R,
则OD=OF=R.
在Rt△BDO中,
由勾股定理,得OB2=BD2+OD2,
即(R+2)2=(2)2+R2,解得R=4,
即☉O的半径是4.
16.解:(1)证明:如图①,连接OB.
∵CB为☉O的切线,切点为B,
∴OB⊥BC,
∴∠OBC=90°,
∴∠OBA+∠CBE=90°.∵OA=OB,
∴∠DAE=∠OBA.
∵CD⊥OA,
∴∠DAE+∠DEA=90°,
∴∠DEA=∠CBE.
又∵∠CEB=∠DEA,
∴∠CEB=∠CBE,∴CB=CE.
(2)证明:如图②,连接OF,OB.
在Rt△ODF中,OF=OA=2OD,
∴∠OFD=30°,∴∠DOF=60°.
∵CD平分,
∴∠AOB=2∠AOF=120°,
∴∠C=360°-∠ODC-∠OBC-∠AOB=60°.
又∵CB=CE,
∴△BCE是等边三角形.
(3)如图③,连接OB,
∵BC是☉O的切线,
∴∠OBC=90°.
又∵∠DCB=45°,
∴△OBC为等腰直角三角形,
∴BC=OB=2,OC=2.
又∵CB=CE,
∴OE=OC-CE=OC-CB=2-2,
∴EF=DF-OE=2-(2-2)=4-2.
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
