2020—2021学年沪科版九年级数学上册第22章相似形单元测试题(word解析版)
文档属性
| 名称 | 2020—2021学年沪科版九年级数学上册第22章相似形单元测试题(word解析版) |
|
|
| 格式 | zip | ||
| 文件大小 | 204.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-31 00:00:00 | ||
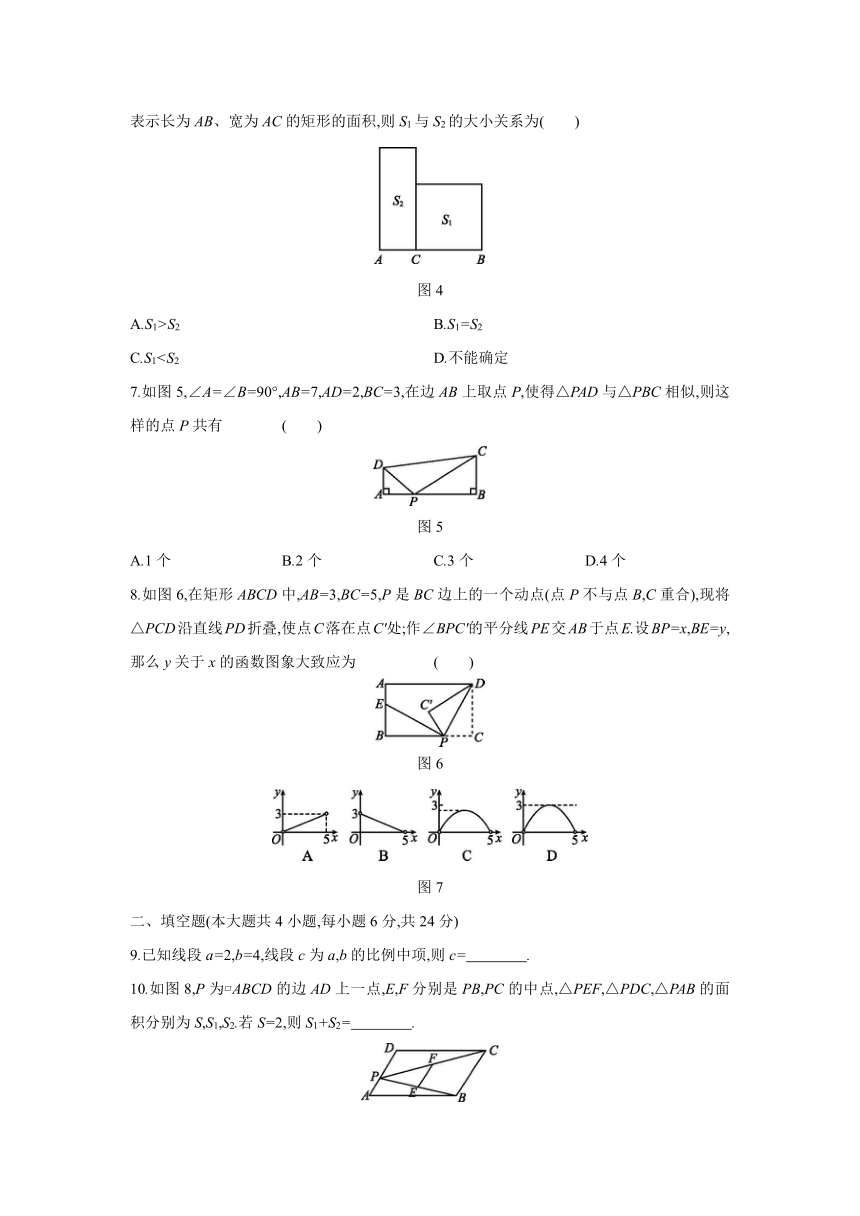
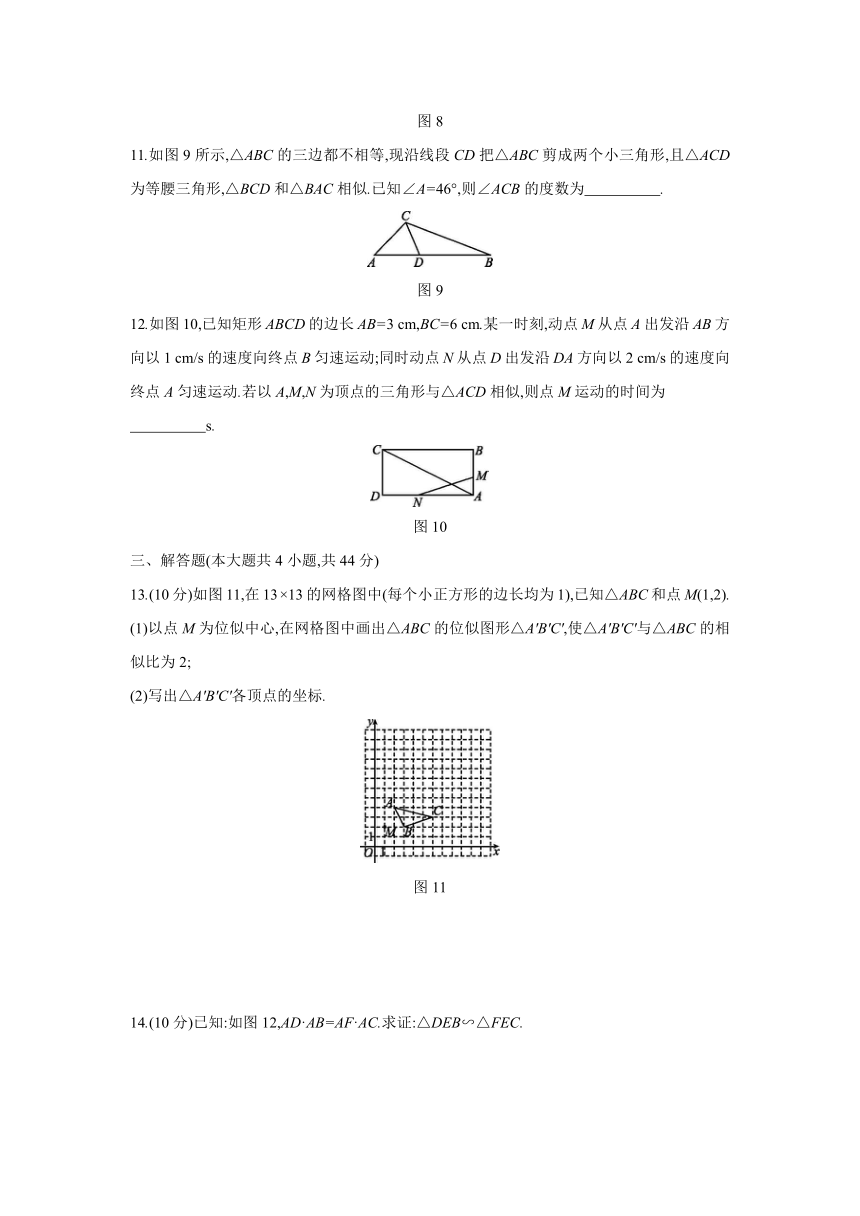
图片预览


文档简介
第22章 相似形
一、选择题(本大题共8小题,每小题4分,共32分)
1.若3x-4y=0,则的值是
( )
A.
B.
C.
D.
2.如图1,在△ABC中,DE∥BC,AQ分别交DE,BC于点P,Q,AD=3,BD=2,则的值为( )
图1
A.
B.
C.
D.
3.已知△ABC的三边长分别为6
cm,7.5
cm,9
cm,△DEF的一边长为4
cm.若这两个三角形相似,则△DEF的另两边长可能为
( )
A.2
cm,3
cm
B.4
cm,5
cm
C.5
cm,6
cm
D.6
cm,7
cm
4.如图2,在?ABCD中,点E在边DC上,DE∶EC=3∶1,连接AE交BD于点F,则△DEF与△BAF的面积之比为
( )
图2
A.3∶4
B.9∶16
C.9∶1
D.3∶1
5.如图3,为测量学校旗杆BC的高度,小东用长为3.2
m的竹竿DE做测量工具,移动竖直的竹竿使竹竿和旗杆BC的顶端的影子恰好落在地面上的同一点A处,此时,竹竿与点A相距8
m,与旗杆相距22
m,则旗杆BC的高为
( )
图3
A.6
m
B.8.8
m
C.12
m
D.30
m
6.如图4,已知C是线段AB的黄金分割点,且BC>AC.若S1表示以BC为边的正方形的面积,S2表示长为AB、宽为AC的矩形的面积,则S1与S2的大小关系为( )
图4
A.S1>S2
B.S1=S2
C.S1D.不能确定
7.如图5,∠A=∠B=90°,AB=7,AD=2,BC=3,在边AB上取点P,使得△PAD与△PBC相似,则这样的点P共有
( )
图5
A.1个
B.2个
C.3个
D.4个
8.如图6,在矩形ABCD中,AB=3,BC=5,P是BC边上的一个动点(点P不与点B,C重合),现将△PCD沿直线PD折叠,使点C落在点C'处;作∠BPC'的平分线PE交AB于点E.设BP=x,BE=y,那么y关于x的函数图象大致应为
( )
图6
图7
二、填空题(本大题共4小题,每小题6分,共24分)
9.已知线段a=2,b=4,线段c为a,b的比例中项,则c= .?
10.如图8,P为?ABCD的边AD上一点,E,F分别是PB,PC的中点,△PEF,△PDC,△PAB的面积分别为S,S1,S2.若S=2,则S1+S2= .?
图8
11.如图9所示,△ABC的三边都不相等,现沿线段CD把△ABC剪成两个小三角形,且△ACD为等腰三角形,△BCD和△BAC相似.已知∠A=46°,则∠ACB的度数为 .?
图9
12.如图10,已知矩形ABCD的边长AB=3
cm,BC=6
cm.某一时刻,动点M从点A出发沿AB方向以1
cm/s的速度向终点B匀速运动;同时动点N从点D出发沿DA方向以2
cm/s的速度向终点A匀速运动.若以A,M,N为顶点的三角形与△ACD相似,则点M运动的时间为
s.?
图10
三、解答题(本大题共4小题,共44分)
13.(10分)如图11,在13×13的网格图中(每个小正方形的边长均为1),已知△ABC和点M(1,2).
(1)以点M为位似中心,在网格图中画出△ABC的位似图形△A'B'C',使△A'B'C'与△ABC的相似比为2;
(2)写出△A'B'C'各顶点的坐标.
图11
14.(10分)已知:如图12,AD·AB=AF·AC.求证:△DEB∽△FEC.
图12
15.(12分)如图13,在△ABC中,AB=AC,AD为BC边上的中线,DE⊥AB于点E.
(1)求证:△BDE∽△CAD;
(2)若AB=13,BC=10,求线段DE的长.
图13
16.(12分)(1)如图14①,在正方形ABCD中,E,F分别是AD,DC边上的点,CE与BF交于点G,BF⊥CE,求证:BF=CE.
(2)如图②,在矩形ABCD中,AB=2AD,E,F分别是AD,DC边上的点,CE与BF交于点G,∠A+∠BGE=180°,求证:CE=2BF.
(3)如图③,若将(2)中的四边形ABCD变为平行四边形,且∠A<90°,其他条件不变,则CE=2BF是否仍然成立?若成立,请证明;若不成立,请说明理由.
图14
答案
1.B
2.[解析]
B 根据平行线所截线段成比例,可得====.
3.[解析]
C 三边对应成比例的两个三角形相似,因为6∶7.5∶9=4∶5∶6,显然选项C符合题意.
4.[解析]
B ∵四边形ABCD为平行四边形,
∴DC∥AB,DC=AB,∴△DEF∽△BAF.
∵DE∶EC=3∶1,∴DE∶DC=3∶4,
∴DE∶AB=3∶4,
∴S△DEF∶S△BAF=9∶16.
故选B.
5.[解析]
C 由题意,得DE∥BC,所以△ADE∽△ABC,得=,即=,解得BC=12(m).
6.[解析]
B ∵C是线段AB的黄金分割点,且BC>AC,∴BC2=AC·AB.
∵S1表示以BC为边的正方形的面积,S2表示长为AB、宽为AC的矩形的面积,
∴S1=BC2,S2=AC·AB,∴S1=S2.故选B.
7.[解析]
C 设AP=x,则BP=AB-AP=7-x.
若△PDA∽△CPB,则=,
即=,解得x=1或x=6.
若△PDA∽△PCB,则=,
即=,解得x=.
则这样的点P共有3个.故选C.
8.[解析]
C 由翻折的性质,得∠CPD=∠C'PD.∵PE平分∠BPC',∴∠BPE=∠C'PE.
∵∠CPD+∠C'PD+∠BPE+∠C'PE=180°,
∴∠BPE+∠CPD=90°.
∵∠C=90°,∴∠CPD+∠CDP=90°,
∴∠BPE=∠CDP.
又∵∠B=∠C=90°,∴△EBP∽△PCD,
∴=,即=,
∴y=x(5-x)=-(x-)2+(0故函数图象为C选项中的图象.
9.[答案]
2
[解析]
∵线段c为a,b的比例中项,
∴c2=ab,即c2=2×4=8,
∴c=2(负值已舍去).
10.[答案]
8
[解析]
因为E,F分别是PB,PC的中点,根据中位线的性质,得EF∥BC,EF=BC,所以△PEF∽△PBC,所以S△PEF∶S△PBC=1∶4.因为S△PEF=S=2,所以S△PBC=8.根据平行四边形的性质,把S1+S2看作整体,求得S1+S2=S△PBC=8.
11.113°或92° [解析]
∵△BCD∽△BAC,
∴∠BCD=∠A=46°.
∵△ACD是等腰三角形,又∠ADC>∠BCD,
∴∠ADC>∠A,即AC≠CD.
①若AC=AD,则∠ACD=∠ADC=(180°-46°)=67°,
∴∠ACB=67°+46°=113°;
②若AD=CD,则∠ACD=∠A=46°,
∴∠ACB=46°+46°=92°.
故答案为113°或92°.
12.[答案]
2.4或1.5
[解析]
设点M运动的时间为t
s,则DN=2t,MA=t,即NA=6-2t.若△ACD∽△MNA,则=,即=,解得t=2.4.经检验,t=2.4是原分式方程的解且符合题意;若△ACD∽△NMA,则=,即=,解得t=1.5.经检验,t=1.5是原分式方程的解且符合题意.故当以A,M,N为顶点的三角形与△ACD相似时,点M运动的时间为2.4
s或1.5
s.
13.解:(1)如图所示,△A'B'C'即为所求.
(2)△A'B'C'的顶点坐标分别为A'(3,6),B'(5,2),C'(11,4).
14.证明:∵AD·AB=AF·AC,∴=.
又∵∠A=∠A,∴△ADC∽△AFB,
∴∠C=∠B.
又∵∠DEB=∠FEC,∴△DEB∽△FEC.
15.解:(1)证明:∵AB=AC,BD=CD,∴AD⊥BC,∠B=∠C.∵DE⊥AB,∴∠DEB=∠ADC=90°,∴△BDE∽△CAD.
(2)由(1)知,AD⊥BC,BD=CD=BC=5.在Rt△ADB中,AD===12.
∵△BDE∽△CAD,∴=,即=,∴DE=.
16.解:(1)证明:∵四边形ABCD是正方形,
∴CD=BC,∠D=∠BCF=90°,
∴∠BCG+∠DCE=90°.
∵BF⊥CE,∴∠BGC=90°,
∴∠CBF+∠BCG=90°,
∴∠DCE=∠CBF,
∴△CDE≌△BCF,
∴BF=CE.
(2)证明:∵四边形ABCD是矩形,
∴CD=AB,BC=AD,∠A=∠D=∠BCD=90°.
∵AB=2AD,∴CD=2BC.
∵∠A+∠BGE=180°,∴∠BGE=90°,
∴∠CGF=∠BGE=90°,
∴∠CFB+∠DCE=90°.
∵∠DEC+∠DCE=90°,
∴∠CFB=∠DEC.
又∵∠D=∠BCF,
∴△CDE∽△BCF,
∴==2,∴CE=2BF.
(3)成立.证明:∵四边形ABCD是平行四边形,
∴∠A=∠BCD,CD=AB,BC=AD.
∵AB=2AD,
∴CD=2BC.
∵∠A+∠BGE=180°,∠BGE+∠BGC=180°,
∴∠BGC=∠A=∠BCD.
又∵∠CBG=∠FBC,∴△BCG∽△BFC,
∴=.
∵∠A+∠D=180°,∠A+∠BGE=∠A+∠CGF=180°,∴∠D=∠CGF.
又∵∠FCG=∠ECD,
∴△CFG∽△CED,∴=,
∴=,∴=,即=.
∵CD=2BC,
∴CE=2BF.
一、选择题(本大题共8小题,每小题4分,共32分)
1.若3x-4y=0,则的值是
( )
A.
B.
C.
D.
2.如图1,在△ABC中,DE∥BC,AQ分别交DE,BC于点P,Q,AD=3,BD=2,则的值为( )
图1
A.
B.
C.
D.
3.已知△ABC的三边长分别为6
cm,7.5
cm,9
cm,△DEF的一边长为4
cm.若这两个三角形相似,则△DEF的另两边长可能为
( )
A.2
cm,3
cm
B.4
cm,5
cm
C.5
cm,6
cm
D.6
cm,7
cm
4.如图2,在?ABCD中,点E在边DC上,DE∶EC=3∶1,连接AE交BD于点F,则△DEF与△BAF的面积之比为
( )
图2
A.3∶4
B.9∶16
C.9∶1
D.3∶1
5.如图3,为测量学校旗杆BC的高度,小东用长为3.2
m的竹竿DE做测量工具,移动竖直的竹竿使竹竿和旗杆BC的顶端的影子恰好落在地面上的同一点A处,此时,竹竿与点A相距8
m,与旗杆相距22
m,则旗杆BC的高为
( )
图3
A.6
m
B.8.8
m
C.12
m
D.30
m
6.如图4,已知C是线段AB的黄金分割点,且BC>AC.若S1表示以BC为边的正方形的面积,S2表示长为AB、宽为AC的矩形的面积,则S1与S2的大小关系为( )
图4
A.S1>S2
B.S1=S2
C.S1
7.如图5,∠A=∠B=90°,AB=7,AD=2,BC=3,在边AB上取点P,使得△PAD与△PBC相似,则这样的点P共有
( )
图5
A.1个
B.2个
C.3个
D.4个
8.如图6,在矩形ABCD中,AB=3,BC=5,P是BC边上的一个动点(点P不与点B,C重合),现将△PCD沿直线PD折叠,使点C落在点C'处;作∠BPC'的平分线PE交AB于点E.设BP=x,BE=y,那么y关于x的函数图象大致应为
( )
图6
图7
二、填空题(本大题共4小题,每小题6分,共24分)
9.已知线段a=2,b=4,线段c为a,b的比例中项,则c= .?
10.如图8,P为?ABCD的边AD上一点,E,F分别是PB,PC的中点,△PEF,△PDC,△PAB的面积分别为S,S1,S2.若S=2,则S1+S2= .?
图8
11.如图9所示,△ABC的三边都不相等,现沿线段CD把△ABC剪成两个小三角形,且△ACD为等腰三角形,△BCD和△BAC相似.已知∠A=46°,则∠ACB的度数为 .?
图9
12.如图10,已知矩形ABCD的边长AB=3
cm,BC=6
cm.某一时刻,动点M从点A出发沿AB方向以1
cm/s的速度向终点B匀速运动;同时动点N从点D出发沿DA方向以2
cm/s的速度向终点A匀速运动.若以A,M,N为顶点的三角形与△ACD相似,则点M运动的时间为
s.?
图10
三、解答题(本大题共4小题,共44分)
13.(10分)如图11,在13×13的网格图中(每个小正方形的边长均为1),已知△ABC和点M(1,2).
(1)以点M为位似中心,在网格图中画出△ABC的位似图形△A'B'C',使△A'B'C'与△ABC的相似比为2;
(2)写出△A'B'C'各顶点的坐标.
图11
14.(10分)已知:如图12,AD·AB=AF·AC.求证:△DEB∽△FEC.
图12
15.(12分)如图13,在△ABC中,AB=AC,AD为BC边上的中线,DE⊥AB于点E.
(1)求证:△BDE∽△CAD;
(2)若AB=13,BC=10,求线段DE的长.
图13
16.(12分)(1)如图14①,在正方形ABCD中,E,F分别是AD,DC边上的点,CE与BF交于点G,BF⊥CE,求证:BF=CE.
(2)如图②,在矩形ABCD中,AB=2AD,E,F分别是AD,DC边上的点,CE与BF交于点G,∠A+∠BGE=180°,求证:CE=2BF.
(3)如图③,若将(2)中的四边形ABCD变为平行四边形,且∠A<90°,其他条件不变,则CE=2BF是否仍然成立?若成立,请证明;若不成立,请说明理由.
图14
答案
1.B
2.[解析]
B 根据平行线所截线段成比例,可得====.
3.[解析]
C 三边对应成比例的两个三角形相似,因为6∶7.5∶9=4∶5∶6,显然选项C符合题意.
4.[解析]
B ∵四边形ABCD为平行四边形,
∴DC∥AB,DC=AB,∴△DEF∽△BAF.
∵DE∶EC=3∶1,∴DE∶DC=3∶4,
∴DE∶AB=3∶4,
∴S△DEF∶S△BAF=9∶16.
故选B.
5.[解析]
C 由题意,得DE∥BC,所以△ADE∽△ABC,得=,即=,解得BC=12(m).
6.[解析]
B ∵C是线段AB的黄金分割点,且BC>AC,∴BC2=AC·AB.
∵S1表示以BC为边的正方形的面积,S2表示长为AB、宽为AC的矩形的面积,
∴S1=BC2,S2=AC·AB,∴S1=S2.故选B.
7.[解析]
C 设AP=x,则BP=AB-AP=7-x.
若△PDA∽△CPB,则=,
即=,解得x=1或x=6.
若△PDA∽△PCB,则=,
即=,解得x=.
则这样的点P共有3个.故选C.
8.[解析]
C 由翻折的性质,得∠CPD=∠C'PD.∵PE平分∠BPC',∴∠BPE=∠C'PE.
∵∠CPD+∠C'PD+∠BPE+∠C'PE=180°,
∴∠BPE+∠CPD=90°.
∵∠C=90°,∴∠CPD+∠CDP=90°,
∴∠BPE=∠CDP.
又∵∠B=∠C=90°,∴△EBP∽△PCD,
∴=,即=,
∴y=x(5-x)=-(x-)2+(0
9.[答案]
2
[解析]
∵线段c为a,b的比例中项,
∴c2=ab,即c2=2×4=8,
∴c=2(负值已舍去).
10.[答案]
8
[解析]
因为E,F分别是PB,PC的中点,根据中位线的性质,得EF∥BC,EF=BC,所以△PEF∽△PBC,所以S△PEF∶S△PBC=1∶4.因为S△PEF=S=2,所以S△PBC=8.根据平行四边形的性质,把S1+S2看作整体,求得S1+S2=S△PBC=8.
11.113°或92° [解析]
∵△BCD∽△BAC,
∴∠BCD=∠A=46°.
∵△ACD是等腰三角形,又∠ADC>∠BCD,
∴∠ADC>∠A,即AC≠CD.
①若AC=AD,则∠ACD=∠ADC=(180°-46°)=67°,
∴∠ACB=67°+46°=113°;
②若AD=CD,则∠ACD=∠A=46°,
∴∠ACB=46°+46°=92°.
故答案为113°或92°.
12.[答案]
2.4或1.5
[解析]
设点M运动的时间为t
s,则DN=2t,MA=t,即NA=6-2t.若△ACD∽△MNA,则=,即=,解得t=2.4.经检验,t=2.4是原分式方程的解且符合题意;若△ACD∽△NMA,则=,即=,解得t=1.5.经检验,t=1.5是原分式方程的解且符合题意.故当以A,M,N为顶点的三角形与△ACD相似时,点M运动的时间为2.4
s或1.5
s.
13.解:(1)如图所示,△A'B'C'即为所求.
(2)△A'B'C'的顶点坐标分别为A'(3,6),B'(5,2),C'(11,4).
14.证明:∵AD·AB=AF·AC,∴=.
又∵∠A=∠A,∴△ADC∽△AFB,
∴∠C=∠B.
又∵∠DEB=∠FEC,∴△DEB∽△FEC.
15.解:(1)证明:∵AB=AC,BD=CD,∴AD⊥BC,∠B=∠C.∵DE⊥AB,∴∠DEB=∠ADC=90°,∴△BDE∽△CAD.
(2)由(1)知,AD⊥BC,BD=CD=BC=5.在Rt△ADB中,AD===12.
∵△BDE∽△CAD,∴=,即=,∴DE=.
16.解:(1)证明:∵四边形ABCD是正方形,
∴CD=BC,∠D=∠BCF=90°,
∴∠BCG+∠DCE=90°.
∵BF⊥CE,∴∠BGC=90°,
∴∠CBF+∠BCG=90°,
∴∠DCE=∠CBF,
∴△CDE≌△BCF,
∴BF=CE.
(2)证明:∵四边形ABCD是矩形,
∴CD=AB,BC=AD,∠A=∠D=∠BCD=90°.
∵AB=2AD,∴CD=2BC.
∵∠A+∠BGE=180°,∴∠BGE=90°,
∴∠CGF=∠BGE=90°,
∴∠CFB+∠DCE=90°.
∵∠DEC+∠DCE=90°,
∴∠CFB=∠DEC.
又∵∠D=∠BCF,
∴△CDE∽△BCF,
∴==2,∴CE=2BF.
(3)成立.证明:∵四边形ABCD是平行四边形,
∴∠A=∠BCD,CD=AB,BC=AD.
∵AB=2AD,
∴CD=2BC.
∵∠A+∠BGE=180°,∠BGE+∠BGC=180°,
∴∠BGC=∠A=∠BCD.
又∵∠CBG=∠FBC,∴△BCG∽△BFC,
∴=.
∵∠A+∠D=180°,∠A+∠BGE=∠A+∠CGF=180°,∴∠D=∠CGF.
又∵∠FCG=∠ECD,
∴△CFG∽△CED,∴=,
∴=,∴=,即=.
∵CD=2BC,
∴CE=2BF.
