苏科版七年级数学上册第6章 平面图形的认识(一)单元测试卷(word含答案)
文档属性
| 名称 | 苏科版七年级数学上册第6章 平面图形的认识(一)单元测试卷(word含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 533.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-31 15:48:14 | ||
图片预览




文档简介
第六单元测试卷
一、选择题(本大题共12小题,每小题3分,共36分
)
1.如图所示,下列说法中正确的是( )
A.∠ADE就是∠D
B.∠ABC可以用∠B表示
C.∠ABC和∠ACB是同一个角
D.∠BAC和∠DAE是不同的两个角
2.点C是线段AB的中点,点D是线段AC的三等分点.若线段,则线段BD的长为(
)
A.10cm
B.8cm
C.8cm或10cm
D.2cm或4cm
3.下列图形中,线段PQ的长度表示点P到直线L的距离的是(
)
A.
B.
C.
D.
4.下列说法正确的是(
)
A.两点之间的距离是两点间的线段
B.与同一条直线垂直的两条直线也垂直
C.同一平面内,过一点有且只有一条直线与已知直线平行
D.同一平面内,过一点有且只有一条直线与已知直线垂直
5.下列日常现象:
①用两根钉子就可以把一根木条固定在墙上;②把弯曲的公路改直,就能够缩短路程;
③利用圆规可以比较两条线段的大小;④建筑工人砌墙时,经常先在两端立桩拉线,然后沿着线砌墙.
其中,可以用“两点确定一条直线”来解释的现象是( )
A.①④
B.②③
C.①②④
D.①③④
6.下列说法①一个角的补角大于这个角②小于平角的角是钝角③同角或等角的余角相等④若,则、、互为补角.其中正确的说法有(
)
A.4个
B.3个
C.2个
D.1个
7.如图,AM为∠BAC的平分线,下列等式错误的是(
)
A.∠BAC=∠BAM
B.∠BAM=∠CAM
C.∠BAM=2∠CAM
D.2∠CAM=∠BAC
8.用一副三角尺,不能画出的角是(
)
A.75°
B.15°
C.135°
D.115°
9.如图,直线AB,CD相交于点O,∠COE是直角,OF平分∠AOD,若∠BOE=40°,则∠AOF的度数是(
)
A.65°
B.60°
C.50°
D.40°
10.某公司员工分别在A、B、C三个住宅区,A区有30人,B区有15人,C区有10人,三个区在一条直线上,位置如图所示,该公司的接送车打算在此间只设一个停靠点,为使所有员工步行到停靠点的路程之和最小,那么停靠点的位置应设在(
)
A.A区
B.B区
C.C区
D.A.?B两区之间
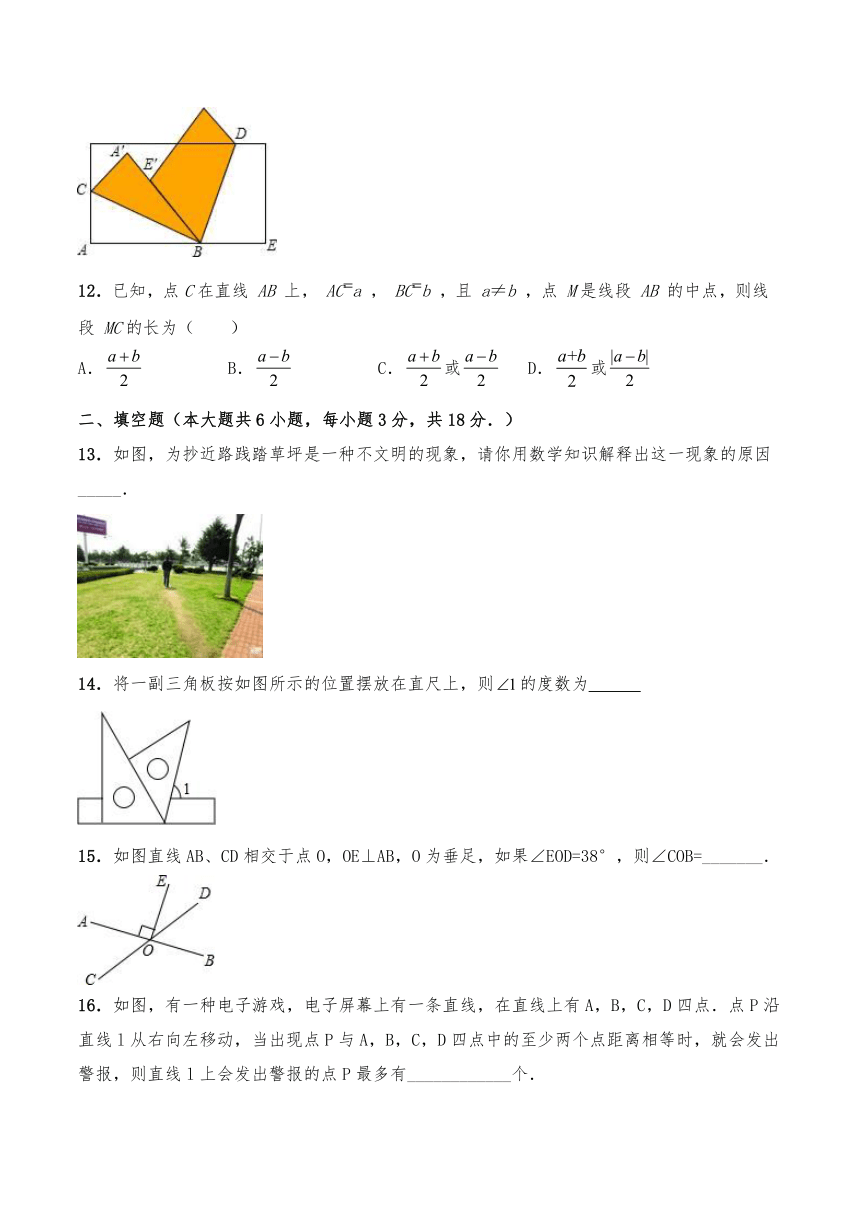
11.如图,将一张长方形纸片的角A、E分别沿着BC、BD折叠,点A落在A'处,点E落在边BA'上的E'处,则∠CBD的度数是( )
A.85°
B.90°
C.95°
D.100°
12.已知,点C在直线
AB
上,
ACa
,
BCb
,且
a≠b
,点
M是线段
AB
的中点,则线段
MC的长为(
)
A.
B.
C.或
D.或
二、填空题(本大题共6小题,每小题3分,共18分.)
13.如图,为抄近路践踏草坪是一种不文明的现象,请你用数学知识解释出这一现象的原因_____.
14.将一副三角板按如图所示的位置摆放在直尺上,则的度数为
15.如图直线AB、CD相交于点O,OE⊥AB,O为垂足,如果∠EOD=38°,则∠COB=_______.
16.如图,有一种电子游戏,电子屏幕上有一条直线,在直线上有A,B,C,D四点.点P沿直线l从右向左移动,当出现点P与A,B,C,D四点中的至少两个点距离相等时,就会发出警报,则直线l上会发出警报的点P最多有____________个.
17.一个电子跳蚤在数轴上做跳跃运动.第一次从原点O起跳,落点为A1,点A1表示的数为1;第二次从点A1起跳,落点为OA1的中点A2;第三次从A2点起跳,落点为0A2的中点A3;如此跳跃下去……最后落点为OA2019的中点A2020.则点A2020表示的数为__________.
18.从12点整开始到1点,经过____分钟,钟表上时针和分针的夹角恰好为99°.
三、解答题(本大题共6小题,共46分.)
19.如图,已知同一平面内的四个点A、B、C、D,根据要求用直尺画图.(1)画线段AB,∠ADC;(2)找一点P,使P点既在直线AD上,又在直线BC上;(3)找一点Q,使Q到A、B、C、D四个点的距离和最短.
20.如图所示的是某风景区的旅游路线示意图,其中B,C,D为风景点,E为两条路的交叉点,图中数据为两相应点间的距离(单位:千米).一位游客从A处出发,以2千米/时的速度步行游览,每个景点的逗留时间均为小时.(1)当他沿着路线A→D→C→E→A游览回到A处时,共用了4小时,求CE的长;(2)若此学生打算从A处出发,步行速度与景点的逗留时间保持不变,且在最短时间内看完三个景点返回到A处,请你为他设计一条步行路线,说明这样设计的理由.
21.如图,从点O引出的射线(任两条不共线)条数与角的总个数有如下关系:从点O引出两条射线形成1个角;如图1从点O引出3条射线共形成3个角;如图2从点O引出4条射线共形成6个角;如图3从点O引出5条射线共形成10个角;
(1)观察操作:当从点O引出6条射线共形成有________个角;
(2)探索发现:如图4当从点O引出n条射线共形成多少个角;(用含n的式子表示)
(3)实践应用:8支篮球队进行单循环比赛(参加比赛的每两支球队之间都要进行一场比赛),总的比赛场数为多少场?如果n支篮球队进行主客场制单循环赛(参加的每个队都与其它所有队各赛2场)总的比赛场数是多少场?
22.
如图,直线AB、CD相交于点O,OE平分∠BOD.(1)若∠AOC=70°,∠DOF=90°,求∠EOF的度数;(2)若OF平分∠COE,∠BOF=15°,若设∠AOE=x°.①用含x的代数式表示∠EOF;②求∠AOC的度数.
23.如图1直角三角板的直角顶点O在直线AB上,OC,OD是三角板的两条直角边,射线OE平分∠AOD.(1)若∠COE=40°,则∠BOD=
.(2)若∠COE=α,求∠BOD(请用含α的代数式表示);(3)当三角板绕O逆时针旋转到图2的位置时,其它条件不变,试猜测∠COE与∠BOD之间有怎样的数量关系?并说明理由.
24.将一副三角板中的两块直角三角尺的直角顶点C按照如图①的方式叠放在一起(∠A=30°,∠ABC=60°,∠E=∠EDC=45°),且三角板ACB的位置保持不动.
(1)将三角板DCE绕点C按顺时针方向旋转至图②,若∠ACE=60°,求∠DCB的度数.
(2)将三角板DCE绕点C按顺时针方向旋转,当旋转到ED∥AB时,求∠BCE的度数(请先在备用图上补全相应的图形).(3)当0°<∠BCE<180°且点E在直线BC的上方时,这两块三角尺是否存在一组边互相平行?若存在,请直接写出∠BCE所有可能的值;若不存在,请说明理由.
25.如图,P是线段AB上一点,AB=12cm,C、D两点分别从P、B出发以1cm/s、2cm/s的速度沿直线AB向左运动(C在线段AP上,D在线段BP上),运动的时间为t.
(1)当t=1时,PD=2AC,请求出AP的长;(2)当t=2时,PD=2AC,请求出AP的长;
(3)若C、D运动到任一时刻时,总有PD=2AC,请求出AP的长;
(4)在(3)的条件下,Q是直线AB上一点,且AQ﹣BQ=PQ,求PQ的长.
26.已知直线AB过点O,∠COD=90°,OE是∠BOC的平分线.(1)操作发现:①如图1,若∠AOC=40°,则∠DOE=
②如图1,若∠AOC=α,则∠DOE=
(用含α的代数式表示)
(2)操作探究:将图1中的∠COD绕顶点O顺时针旋转到图2的位置,其他条件不变,②中的结论是否成立?试说明理由.(3)拓展应用:将图2中的∠COD绕顶点O逆时针旋转到图3的位置,其他条件不变,若∠AOC=α,求∠DOE的度数,(用含α的代数式表示)
答案
一、选择题
1.B
2.C
3.C
4.D
5.A
6.D
7.C
8.D
9.A
10.A
11.B
12.D
二、填空题
13.两点之间线段最短
14.
15.128°
16.6
17.
18.18或
三、解答题
19.解:(1)如图所示,线段AB、∠ADC即为所求;(2)直线AD与直线BC交点P即为所求;
(3)如图所示,点Q即为所求.
20.(1)设CE长为x千米,则2.2+1.4+x+1.2=2×(4-2×0.75),解得:x=0.2(千米).
(2)若步行路线为A→D→C→B→E→A(或A→E→B→C→D→A),则所用时间为:
(2.2+1.4+2+0.6+1.2)÷2+3×0.75=5.95(小时).
若步行路线为A→D→C→E→B→E→A(或A→E→B→E→C→D→A),则所用时间为:
(2.2+1.4+0.2+0.6×2+1.2)÷2+3×0.75=5.35(小时).
因为5.95>5.35,所以步行路线应为A→D→C→E→B→E→A(或A→E→B→E→C→D→A).
21.解:(1)现察图形可知,2条射线组成1个角,3条射线就可以组成2+1=3个角,4条射线可以组成3+2+1=6个角,依此可得6条射线组成角的个数是1+2+3+4+5=15;
(2)根据(1)的规律可知:n条射线组成角的个数是1+2+3+…+(n-1)=;
(3)将每只球队当作一条射线,每场单循环赛当作一个角,所以8支篮球队进行单循环比赛相当于8条射线可以组成的角,即比赛场数=28;
如果n支篮球队进行主客场制单循环赛(参加的每个队都与其它所有队各赛2场)总的比赛场数是×2=
n(n-1).
故答案为(1)15,(2),(3)28,
n(n-1).
22.
(1)由对顶角相等可知:∠BOD=∠AOC=70°,
∵∠FOB=∠DOF-∠BOD,∴∠FOB=90°-70°=20°,
∵OE平分∠BOD,∴∠BOE=∠BOD=×70°=35°,
∴∠EOF=∠FOB+∠BOE=35°+20°=55°.
(2)①∵OE平分∠BOD,∴∠BOE=∠DOE,
∵∠BOE+∠AOE=180°,∠COE+∠DOE=180°,∴∠COE=∠AOE=x,
∵OF平分∠COE,∴∠FOE=x.
②∵∠BOE=∠FOE-∠FOB,∴∠BOE=x-15°,
∵∠BOE+∠AOE=180°,∴x-15°+x=180°,解得x=130°,
∴∠AOC=2∠BOE=2×(180°-130°)=100°.
23.解:(1)若∠COE=40°,∵∠COD=90°,∴∠EOD=90°﹣40°=50°,
∵OE平分∠AOD,∴∠AOD=2∠EOD=100°,∴∠BOD=180°﹣100°=80°;
(2)∵∠COE=α,∴∠EOD=90﹣α,
∵OE平分∠AOD,∴∠AOD=2∠EOD=2(90﹣α)=180﹣2α,
∴∠BOD=180°﹣(180﹣2α)=2α;
(3)如图2,∠BOD+2∠COE=360°,理由是:设∠BOD=β,则∠AOD=180°﹣β,
∵OE平分∠AOD,∴∠EOD=
∠AOD=
=90°﹣β,
∵∠COD=90°,∴∠COE=90°+(90°﹣β)=180°﹣β,
即∠BOD+2∠COE=360°.
故答案为:(1)80°;(2)2α;(3)∠BOD+2∠COE=360°,理由见详解.
24.解:(1)如图中,
∵∠ACB=∠ECD=90°,∴∠ECB=∠ACD,
∵∠ACE=60°,∴∠BCE=∠ACD=30°,∴∠BCD=∠BCE+∠ECD=30°+90°=120°,故答案为120°;
(2)如图中,
当DE∥AB时,延长BC交DE于M,∴∠B=∠DMC=60°,
∵∠DMC=∠E+∠MCE,∴∠ECM=15°,∴∠BCE=165°,
当D′E′∥AB时,∠E′CB=∠ECM=15°,∴当ED∥AB时,∠BCE的度数为165°或15°;
(3)存在.如图,①CD∥AB时,∠BCE=30°,②DE∥BC时,∠BCE=45°,③CE∥AB时,∠BCE=120°,
④DE∥AB时,∠BCE=165°,⑤当AC∥DE时,∠BCE=135°
综上所述,当0°<∠BCE<180°且点E在直线BC的上方时,这两块三角尺存在一组边互相平行,∠BCE
的值为30°或45°或120°或165°或135°.
25.(1)
因为点C从P出发以1(cm/s)的速度运动,运动的时间为t=1(s),所以(cm).
因为点D从B出发以2(cm/s)的速度运动,运动的时间为t=1(s),所以(cm).故BD=2PC.
因为PD=2AC,BD=2PC,所以BD+PD=2(PC+AC),即PB=2AP.故AB=AP+PB=3AP.
因为AB=12cm,所以(cm).
(2)
因为点C从P出发以1(cm/s)的速度运动,运动的时间为t=2(s),所以(cm).
因为点D从B出发以2(cm/s)的速度运动,运动的时间为t=2(s),所以(cm).故BD=2PC.
因为PD=2AC,BD=2PC,所以BD+PD=2(PC+AC),即PB=2AP.故AB=AP+PB=3AP.
因为AB=12cm,所以(cm).
(3)
因为点C从P出发以1(cm/s)的速度运动,运动的时间为t(s),所以(cm).
因为点D从B出发以2(cm/s)的速度运动,运动的时间为t(s),所以(cm).故BD=2PC.
因为PD=2AC,BD=2PC,所以BD+PD=2(PC+AC),即PB=2AP.故AB=AP+PB=3AP.
因为AB=12cm,所以(cm).
(4)
本题需要对以下两种情况分别进行讨论.
(i)
点Q在线段AB上(如图①).因为AQ-BQ=PQ,所以AQ=PQ+BQ.
因为AQ=AP+PQ,所以AP=BQ.因为,所以.
故.因为AB=12cm,所以(cm).
(ii)
点Q不在线段AB上,则点Q在线段AB的延长线上(如图②).
因为AQ-BQ=PQ,所以AQ=PQ+BQ.因为AQ=AP+PQ,所以AP=BQ.
因为,所以.故.
因为AB=12cm,所以(cm).
综上所述,PQ的长为4cm或12cm.
26.解:(1)如图1,∵∠COD=90°,∴∠AOC+∠BOD=90°,
∵∠AOC=40°,∴∠BOD=50°,∴∠BOC=∠COD+∠BOD=90°+50°=140°,
∵OE平分∠BOC,∴∠BOE=∠BOC=70°,∴∠DOE=∠BOE-∠BOD=20°,
②如图1,由(1)知:∠AOC+∠BOD=90°,
∵∠AOC=α,∴∠BOD=90°﹣α,∴∠BOC=∠COD+∠BOD=90°+90°﹣α=180°﹣α,
∵OE平分∠BOC,∴∠BOE=∠BOC=90°﹣α,
∴∠DOE=∠BOE﹣∠BOD=90°﹣α﹣(90°﹣α)=α,
(2)(1)中的结论还成立,理由是:
如图2,∵∠AOC+∠BOC=180°,∠AOC=α,∴∠BOC=180°﹣α,
∵OE平分∠BOC,∴∠EOC=∠BOC=90°﹣α,
∵∠COD=90°,∴∠DOE=∠COD﹣∠COE=90°﹣(90°﹣α)=α;
(3)如图3,∵∠AOC+∠BOC=180°,∠AOC=α,∴∠BOC=180°﹣α,
∵OE平分∠BOC,∴∠EOC=∠BOC=90°﹣α,
∵∠COD=90°,∴∠DOE=∠COD+∠COE=90°+(90°﹣α)=180°﹣α.
一、选择题(本大题共12小题,每小题3分,共36分
)
1.如图所示,下列说法中正确的是( )
A.∠ADE就是∠D
B.∠ABC可以用∠B表示
C.∠ABC和∠ACB是同一个角
D.∠BAC和∠DAE是不同的两个角
2.点C是线段AB的中点,点D是线段AC的三等分点.若线段,则线段BD的长为(
)
A.10cm
B.8cm
C.8cm或10cm
D.2cm或4cm
3.下列图形中,线段PQ的长度表示点P到直线L的距离的是(
)
A.
B.
C.
D.
4.下列说法正确的是(
)
A.两点之间的距离是两点间的线段
B.与同一条直线垂直的两条直线也垂直
C.同一平面内,过一点有且只有一条直线与已知直线平行
D.同一平面内,过一点有且只有一条直线与已知直线垂直
5.下列日常现象:
①用两根钉子就可以把一根木条固定在墙上;②把弯曲的公路改直,就能够缩短路程;
③利用圆规可以比较两条线段的大小;④建筑工人砌墙时,经常先在两端立桩拉线,然后沿着线砌墙.
其中,可以用“两点确定一条直线”来解释的现象是( )
A.①④
B.②③
C.①②④
D.①③④
6.下列说法①一个角的补角大于这个角②小于平角的角是钝角③同角或等角的余角相等④若,则、、互为补角.其中正确的说法有(
)
A.4个
B.3个
C.2个
D.1个
7.如图,AM为∠BAC的平分线,下列等式错误的是(
)
A.∠BAC=∠BAM
B.∠BAM=∠CAM
C.∠BAM=2∠CAM
D.2∠CAM=∠BAC
8.用一副三角尺,不能画出的角是(
)
A.75°
B.15°
C.135°
D.115°
9.如图,直线AB,CD相交于点O,∠COE是直角,OF平分∠AOD,若∠BOE=40°,则∠AOF的度数是(
)
A.65°
B.60°
C.50°
D.40°
10.某公司员工分别在A、B、C三个住宅区,A区有30人,B区有15人,C区有10人,三个区在一条直线上,位置如图所示,该公司的接送车打算在此间只设一个停靠点,为使所有员工步行到停靠点的路程之和最小,那么停靠点的位置应设在(
)
A.A区
B.B区
C.C区
D.A.?B两区之间
11.如图,将一张长方形纸片的角A、E分别沿着BC、BD折叠,点A落在A'处,点E落在边BA'上的E'处,则∠CBD的度数是( )
A.85°
B.90°
C.95°
D.100°
12.已知,点C在直线
AB
上,
ACa
,
BCb
,且
a≠b
,点
M是线段
AB
的中点,则线段
MC的长为(
)
A.
B.
C.或
D.或
二、填空题(本大题共6小题,每小题3分,共18分.)
13.如图,为抄近路践踏草坪是一种不文明的现象,请你用数学知识解释出这一现象的原因_____.
14.将一副三角板按如图所示的位置摆放在直尺上,则的度数为
15.如图直线AB、CD相交于点O,OE⊥AB,O为垂足,如果∠EOD=38°,则∠COB=_______.
16.如图,有一种电子游戏,电子屏幕上有一条直线,在直线上有A,B,C,D四点.点P沿直线l从右向左移动,当出现点P与A,B,C,D四点中的至少两个点距离相等时,就会发出警报,则直线l上会发出警报的点P最多有____________个.
17.一个电子跳蚤在数轴上做跳跃运动.第一次从原点O起跳,落点为A1,点A1表示的数为1;第二次从点A1起跳,落点为OA1的中点A2;第三次从A2点起跳,落点为0A2的中点A3;如此跳跃下去……最后落点为OA2019的中点A2020.则点A2020表示的数为__________.
18.从12点整开始到1点,经过____分钟,钟表上时针和分针的夹角恰好为99°.
三、解答题(本大题共6小题,共46分.)
19.如图,已知同一平面内的四个点A、B、C、D,根据要求用直尺画图.(1)画线段AB,∠ADC;(2)找一点P,使P点既在直线AD上,又在直线BC上;(3)找一点Q,使Q到A、B、C、D四个点的距离和最短.
20.如图所示的是某风景区的旅游路线示意图,其中B,C,D为风景点,E为两条路的交叉点,图中数据为两相应点间的距离(单位:千米).一位游客从A处出发,以2千米/时的速度步行游览,每个景点的逗留时间均为小时.(1)当他沿着路线A→D→C→E→A游览回到A处时,共用了4小时,求CE的长;(2)若此学生打算从A处出发,步行速度与景点的逗留时间保持不变,且在最短时间内看完三个景点返回到A处,请你为他设计一条步行路线,说明这样设计的理由.
21.如图,从点O引出的射线(任两条不共线)条数与角的总个数有如下关系:从点O引出两条射线形成1个角;如图1从点O引出3条射线共形成3个角;如图2从点O引出4条射线共形成6个角;如图3从点O引出5条射线共形成10个角;
(1)观察操作:当从点O引出6条射线共形成有________个角;
(2)探索发现:如图4当从点O引出n条射线共形成多少个角;(用含n的式子表示)
(3)实践应用:8支篮球队进行单循环比赛(参加比赛的每两支球队之间都要进行一场比赛),总的比赛场数为多少场?如果n支篮球队进行主客场制单循环赛(参加的每个队都与其它所有队各赛2场)总的比赛场数是多少场?
22.
如图,直线AB、CD相交于点O,OE平分∠BOD.(1)若∠AOC=70°,∠DOF=90°,求∠EOF的度数;(2)若OF平分∠COE,∠BOF=15°,若设∠AOE=x°.①用含x的代数式表示∠EOF;②求∠AOC的度数.
23.如图1直角三角板的直角顶点O在直线AB上,OC,OD是三角板的两条直角边,射线OE平分∠AOD.(1)若∠COE=40°,则∠BOD=
.(2)若∠COE=α,求∠BOD(请用含α的代数式表示);(3)当三角板绕O逆时针旋转到图2的位置时,其它条件不变,试猜测∠COE与∠BOD之间有怎样的数量关系?并说明理由.
24.将一副三角板中的两块直角三角尺的直角顶点C按照如图①的方式叠放在一起(∠A=30°,∠ABC=60°,∠E=∠EDC=45°),且三角板ACB的位置保持不动.
(1)将三角板DCE绕点C按顺时针方向旋转至图②,若∠ACE=60°,求∠DCB的度数.
(2)将三角板DCE绕点C按顺时针方向旋转,当旋转到ED∥AB时,求∠BCE的度数(请先在备用图上补全相应的图形).(3)当0°<∠BCE<180°且点E在直线BC的上方时,这两块三角尺是否存在一组边互相平行?若存在,请直接写出∠BCE所有可能的值;若不存在,请说明理由.
25.如图,P是线段AB上一点,AB=12cm,C、D两点分别从P、B出发以1cm/s、2cm/s的速度沿直线AB向左运动(C在线段AP上,D在线段BP上),运动的时间为t.
(1)当t=1时,PD=2AC,请求出AP的长;(2)当t=2时,PD=2AC,请求出AP的长;
(3)若C、D运动到任一时刻时,总有PD=2AC,请求出AP的长;
(4)在(3)的条件下,Q是直线AB上一点,且AQ﹣BQ=PQ,求PQ的长.
26.已知直线AB过点O,∠COD=90°,OE是∠BOC的平分线.(1)操作发现:①如图1,若∠AOC=40°,则∠DOE=
②如图1,若∠AOC=α,则∠DOE=
(用含α的代数式表示)
(2)操作探究:将图1中的∠COD绕顶点O顺时针旋转到图2的位置,其他条件不变,②中的结论是否成立?试说明理由.(3)拓展应用:将图2中的∠COD绕顶点O逆时针旋转到图3的位置,其他条件不变,若∠AOC=α,求∠DOE的度数,(用含α的代数式表示)
答案
一、选择题
1.B
2.C
3.C
4.D
5.A
6.D
7.C
8.D
9.A
10.A
11.B
12.D
二、填空题
13.两点之间线段最短
14.
15.128°
16.6
17.
18.18或
三、解答题
19.解:(1)如图所示,线段AB、∠ADC即为所求;(2)直线AD与直线BC交点P即为所求;
(3)如图所示,点Q即为所求.
20.(1)设CE长为x千米,则2.2+1.4+x+1.2=2×(4-2×0.75),解得:x=0.2(千米).
(2)若步行路线为A→D→C→B→E→A(或A→E→B→C→D→A),则所用时间为:
(2.2+1.4+2+0.6+1.2)÷2+3×0.75=5.95(小时).
若步行路线为A→D→C→E→B→E→A(或A→E→B→E→C→D→A),则所用时间为:
(2.2+1.4+0.2+0.6×2+1.2)÷2+3×0.75=5.35(小时).
因为5.95>5.35,所以步行路线应为A→D→C→E→B→E→A(或A→E→B→E→C→D→A).
21.解:(1)现察图形可知,2条射线组成1个角,3条射线就可以组成2+1=3个角,4条射线可以组成3+2+1=6个角,依此可得6条射线组成角的个数是1+2+3+4+5=15;
(2)根据(1)的规律可知:n条射线组成角的个数是1+2+3+…+(n-1)=;
(3)将每只球队当作一条射线,每场单循环赛当作一个角,所以8支篮球队进行单循环比赛相当于8条射线可以组成的角,即比赛场数=28;
如果n支篮球队进行主客场制单循环赛(参加的每个队都与其它所有队各赛2场)总的比赛场数是×2=
n(n-1).
故答案为(1)15,(2),(3)28,
n(n-1).
22.
(1)由对顶角相等可知:∠BOD=∠AOC=70°,
∵∠FOB=∠DOF-∠BOD,∴∠FOB=90°-70°=20°,
∵OE平分∠BOD,∴∠BOE=∠BOD=×70°=35°,
∴∠EOF=∠FOB+∠BOE=35°+20°=55°.
(2)①∵OE平分∠BOD,∴∠BOE=∠DOE,
∵∠BOE+∠AOE=180°,∠COE+∠DOE=180°,∴∠COE=∠AOE=x,
∵OF平分∠COE,∴∠FOE=x.
②∵∠BOE=∠FOE-∠FOB,∴∠BOE=x-15°,
∵∠BOE+∠AOE=180°,∴x-15°+x=180°,解得x=130°,
∴∠AOC=2∠BOE=2×(180°-130°)=100°.
23.解:(1)若∠COE=40°,∵∠COD=90°,∴∠EOD=90°﹣40°=50°,
∵OE平分∠AOD,∴∠AOD=2∠EOD=100°,∴∠BOD=180°﹣100°=80°;
(2)∵∠COE=α,∴∠EOD=90﹣α,
∵OE平分∠AOD,∴∠AOD=2∠EOD=2(90﹣α)=180﹣2α,
∴∠BOD=180°﹣(180﹣2α)=2α;
(3)如图2,∠BOD+2∠COE=360°,理由是:设∠BOD=β,则∠AOD=180°﹣β,
∵OE平分∠AOD,∴∠EOD=
∠AOD=
=90°﹣β,
∵∠COD=90°,∴∠COE=90°+(90°﹣β)=180°﹣β,
即∠BOD+2∠COE=360°.
故答案为:(1)80°;(2)2α;(3)∠BOD+2∠COE=360°,理由见详解.
24.解:(1)如图中,
∵∠ACB=∠ECD=90°,∴∠ECB=∠ACD,
∵∠ACE=60°,∴∠BCE=∠ACD=30°,∴∠BCD=∠BCE+∠ECD=30°+90°=120°,故答案为120°;
(2)如图中,
当DE∥AB时,延长BC交DE于M,∴∠B=∠DMC=60°,
∵∠DMC=∠E+∠MCE,∴∠ECM=15°,∴∠BCE=165°,
当D′E′∥AB时,∠E′CB=∠ECM=15°,∴当ED∥AB时,∠BCE的度数为165°或15°;
(3)存在.如图,①CD∥AB时,∠BCE=30°,②DE∥BC时,∠BCE=45°,③CE∥AB时,∠BCE=120°,
④DE∥AB时,∠BCE=165°,⑤当AC∥DE时,∠BCE=135°
综上所述,当0°<∠BCE<180°且点E在直线BC的上方时,这两块三角尺存在一组边互相平行,∠BCE
的值为30°或45°或120°或165°或135°.
25.(1)
因为点C从P出发以1(cm/s)的速度运动,运动的时间为t=1(s),所以(cm).
因为点D从B出发以2(cm/s)的速度运动,运动的时间为t=1(s),所以(cm).故BD=2PC.
因为PD=2AC,BD=2PC,所以BD+PD=2(PC+AC),即PB=2AP.故AB=AP+PB=3AP.
因为AB=12cm,所以(cm).
(2)
因为点C从P出发以1(cm/s)的速度运动,运动的时间为t=2(s),所以(cm).
因为点D从B出发以2(cm/s)的速度运动,运动的时间为t=2(s),所以(cm).故BD=2PC.
因为PD=2AC,BD=2PC,所以BD+PD=2(PC+AC),即PB=2AP.故AB=AP+PB=3AP.
因为AB=12cm,所以(cm).
(3)
因为点C从P出发以1(cm/s)的速度运动,运动的时间为t(s),所以(cm).
因为点D从B出发以2(cm/s)的速度运动,运动的时间为t(s),所以(cm).故BD=2PC.
因为PD=2AC,BD=2PC,所以BD+PD=2(PC+AC),即PB=2AP.故AB=AP+PB=3AP.
因为AB=12cm,所以(cm).
(4)
本题需要对以下两种情况分别进行讨论.
(i)
点Q在线段AB上(如图①).因为AQ-BQ=PQ,所以AQ=PQ+BQ.
因为AQ=AP+PQ,所以AP=BQ.因为,所以.
故.因为AB=12cm,所以(cm).
(ii)
点Q不在线段AB上,则点Q在线段AB的延长线上(如图②).
因为AQ-BQ=PQ,所以AQ=PQ+BQ.因为AQ=AP+PQ,所以AP=BQ.
因为,所以.故.
因为AB=12cm,所以(cm).
综上所述,PQ的长为4cm或12cm.
26.解:(1)如图1,∵∠COD=90°,∴∠AOC+∠BOD=90°,
∵∠AOC=40°,∴∠BOD=50°,∴∠BOC=∠COD+∠BOD=90°+50°=140°,
∵OE平分∠BOC,∴∠BOE=∠BOC=70°,∴∠DOE=∠BOE-∠BOD=20°,
②如图1,由(1)知:∠AOC+∠BOD=90°,
∵∠AOC=α,∴∠BOD=90°﹣α,∴∠BOC=∠COD+∠BOD=90°+90°﹣α=180°﹣α,
∵OE平分∠BOC,∴∠BOE=∠BOC=90°﹣α,
∴∠DOE=∠BOE﹣∠BOD=90°﹣α﹣(90°﹣α)=α,
(2)(1)中的结论还成立,理由是:
如图2,∵∠AOC+∠BOC=180°,∠AOC=α,∴∠BOC=180°﹣α,
∵OE平分∠BOC,∴∠EOC=∠BOC=90°﹣α,
∵∠COD=90°,∴∠DOE=∠COD﹣∠COE=90°﹣(90°﹣α)=α;
(3)如图3,∵∠AOC+∠BOC=180°,∠AOC=α,∴∠BOC=180°﹣α,
∵OE平分∠BOC,∴∠EOC=∠BOC=90°﹣α,
∵∠COD=90°,∴∠DOE=∠COD+∠COE=90°+(90°﹣α)=180°﹣α.
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
