2020--2021学年苏科版九年级数学上册 第3章:数据的集中趋势和离散程度 单元测试(word版含答案)
文档属性
| 名称 | 2020--2021学年苏科版九年级数学上册 第3章:数据的集中趋势和离散程度 单元测试(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 650.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-31 17:04:05 | ||
图片预览




文档简介
苏教版九上数据的集中趋势和离散程度单元测试
一、单选题(1-10题,每题3分,共30分)
1.一组数据4,2,x,3,9的平均数为4,则这组数据的众数和中位数分别是( )
A.3,2
B.2,2
C.2,3
D.2,4
2.面试时,某应聘者的学历、经验和工作态度的得分分别是72分、86分、60分,若依次按照1:3:2的比例确定成绩,则该应聘者的最终成绩是(
)
A.75
B.72
C.70
D.65
3.下列说法正确的是( )
A.一组数据3,5,4,5,6,7的众数、中位数和平均数都是5
B.为了解某灯管的使用寿命,可以采用普查的方式进行
C.两组身高数据的方差分别是S2甲=0.01,S2乙=0.02,那么乙组的身高比较整齐
D.“清明时节雨纷纷”是必然事件
4.我校七年级举行大合唱比赛,六位评委给七年级一班的打分如下:(单位:分),则该班得分的平均分为(
)
A.9.45分
B.9.50分
C.9.55分
D.9.60分
5.某学习小组9名学生参加“数学竞赛”,他们的得分情况如下表:
人数(人)
1
3
4
1
分数(分)
80
85
90
95
那么这9名学生所得分数的众数和中位数分别是(
)
A.90,87.5
B.90,85
C.90,90
D.85,85
6.为了更好地迎接庐阳区排球比赛,某校积极准备,从全校学生中遴选出21名同学进行相应的排球训练,该训练队成员的身高如下表:
身高(cm)
170
172
175
178
180
182
185
人数(个)
2
4
5
2
4
3
1
则该校排球队21名同学身高的众数和中位数分别是(单位:cm)( )
A.185,178
B.178,175
C.175,178
D.175,175
7.某企业复工之后,举行了一个简单的技工比赛,参赛的五名选手在单位时间内加工零件的合格率分别为:94.3%
,96.1%
,
94.3%
,91.7%
,93.5%.关于这组数据,下列说法正确的是( )
A.平均数是93.96%
B.方差是0
C.中位数是93.5%
D.众数是94.3%
8.在某中学举行的演讲比赛中,八年级5名参赛选手的成绩如下表所示,请你根据表中提供的数据,计算出这5名选手成绩的方差为( )
A.2
B.6.8
C.34
D.93
9.下表记录了甲、乙、丙、丁四名射击运动员最近几次选拔赛成绩的平均数和方差.根据表中数据,要从中选择一名成绩好且又发挥稳定的运动员参加比赛,应选择(
)
甲
乙
丙
丁
平均数(环)
9.14
9.15
9.14
9.15
方差
6.6
6.8
6.7
6.6
A.甲
B.乙
C.丙
D.丁
10.某单位招聘一名员工,从专业知识、工作业绩、面试成绩三个方面进行考核(考核的满分均为100分)方面的权重比依次为2∶4∶4.小明经过考核后所得的分数依次为90,85,80分,那么小明考核的最后得分是(
)
A.80
B.84
C.87
D.90
二、填空题(11-18题,每题2分,共16分)
11.小明五次测试成绩为:91、89、88、90、92,则五次测试成绩平均数为_____,方差为________.
12.如图是小明家今年1月份至5月份的每月用电量的统计图,据此推断他家这五个月的月平均用电量是_____度.
13.某班五个兴趣小组的人数分别为4,4,5,x,6,已知这组数据的平均数是5,则这组数据的中位数是_____.
14.2010年4月14日青海省玉树县发生7.1级大地震后,杭州浦阳中学九年级(5)班的42名同学踊跃捐款.有20人每人捐5元、11人每人捐10元、10人每人捐20元、1人捐100元.在这次每人捐款的数值中,中位数是____
15.一组数据-1、2、5、x的极差为8,则
x=_________.
16.已知一组数据x1,x2,x3,x4的平均数是5,则数据x1+3,x2+3,x3+3,x4+3的平均数是____.
17.甲乙两台机床生产同一种零件,并且每天产量相等,在6天众每天生产零件中的次品数依次是:甲:3、0、0、2、0、1、;乙:1、0、2、1、0、2.则甲、乙两台机床中性能较稳定的是______.
18.甲、乙、丙三名射击手的20次测试的平均成绩都是8环,方差分别(环2),(环2),(环2),则成绩最稳定的是________.
三、解答题(共74分)
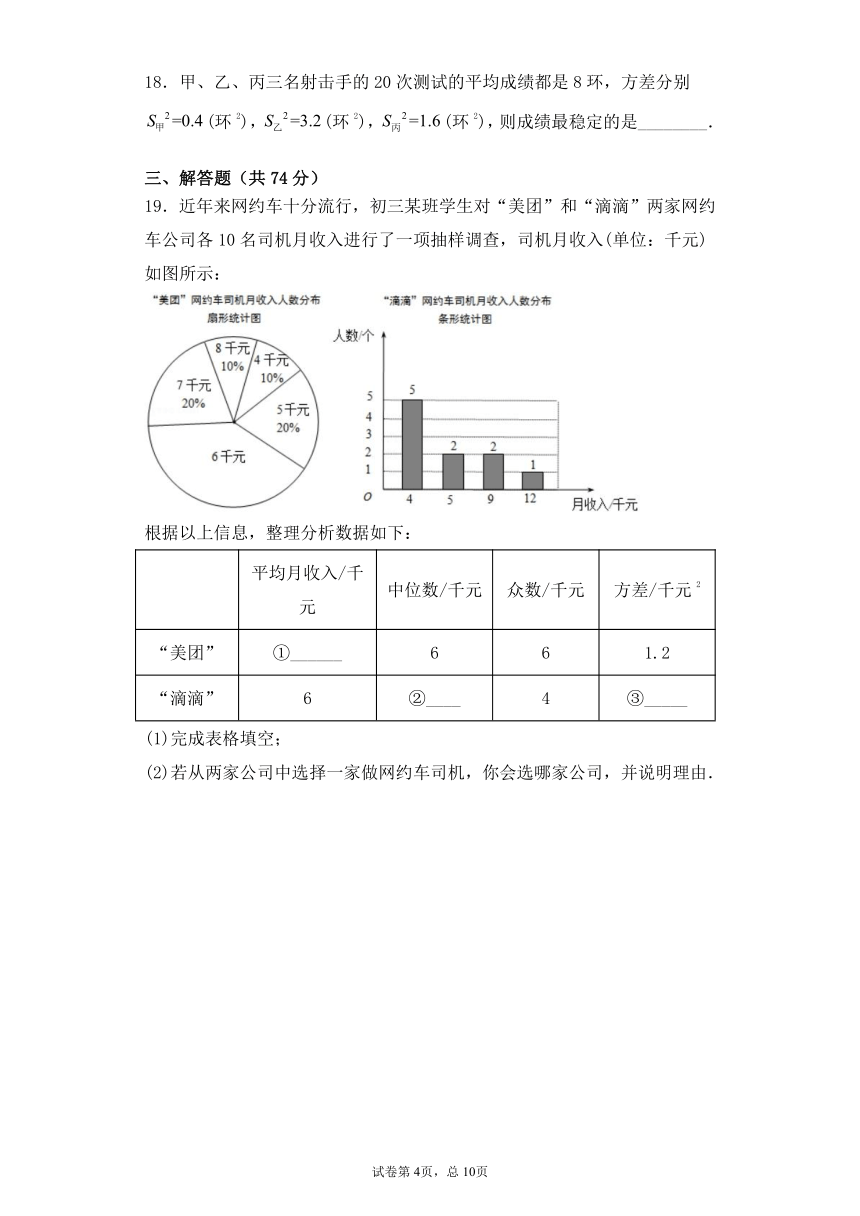
19.近年来网约车十分流行,初三某班学生对“美团”和“滴滴”两家网约车公司各10名司机月收入进行了一项抽样调查,司机月收入(单位:千元)如图所示:
根据以上信息,整理分析数据如下:
平均月收入/千元
中位数/千元
众数/千元
方差/千元2
“美团”
①______
6
6
1.2
“滴滴”
6
②____
4
③_____
(1)完成表格填空;
(2)若从两家公司中选择一家做网约车司机,你会选哪家公司,并说明理由.
20.某村深入贯彻落实习近平新时代中国特色社会主义思想,认真践行“绿水青山就是金山银山”理念.在外打工的王大叔返回家乡创业,承包了一座荒山,栽了1000棵小枣树,发现成活率均为90%,并已挂果.为了分析收成情况,他从这座山上随意采摘了6棵树上的小枣,每棵的产量(千克)如下:48
36
42
36
36
42
(1)这组数据的极差、平均数、中位数、众数如表所示:
极差
平均数
中位数
众数
(2)这座山的枣子采摘后全部被某加工厂收购去进行精加工,经过两道工序的加工筛选后,最后筛选到合格的枣子总量为23040千克,平均每道工序筛选的损耗率是多少?
21.某校八年级(1)班甲、乙两男生在5次引体向上测试中有效次数如下:
甲:8,8,7,8,9;乙:5,9,7,10,9;
甲乙两同学引体向上的平均数、众数、中位数、方差如下:
平均数
众数
中位数
方差
甲
8
b
8
0.4
乙
a
9
c
3.2
根据以上信息,回答下列问题:
(1)表格是a= ,b= ,c= .(填数值)
(2)体育老师根据这5次的成绩,决定选择甲同学代表班级参加年级引体向上比赛,选择甲的理由是
.班主任李老师根据去年比赛的成绩(至少9次才能获奖),决定选择乙同学代表班级参加年级引体向上比赛,选择乙的理由是
;
(3)如果乙同学再做一次引体向上,有效次数为8,那么乙同学6次引体向上成绩的平均数
,中位数
,方差
.(填“变大”、“变小”或“不变”)
22.某市团委举办“我的中国梦”为主题的知识竞赛,甲、乙两所学校参赛人数相等,比赛结束后,发现学生成绩分别为70分,80分,90分,100分,并根据统计数据绘制了如下不完整的统计图表:
(1)在图①中,“80分”所在扇形的圆心角度数为 ;在图②中,“100分”的有 人;
(2)甲校成绩的中位数为 ;
(3)求乙校成绩的平均分;
(4)经计算知S甲2=135,S乙2=175,请你根据这两个数据,对甲、乙两校成绩作出合理评价.
23.为加强抗击疫情的教育宣传,某中学开展防疫知识线上竞赛活动,八年级(1)、(2)班各选出5名选手参加竞赛,两个班各选出的名选手的竞赛成绩(满分为分)如图所示:
(1)请你计算两个班的平均成绩各是多少分;
(2)写出两个班竞赛成绩的中位数,结合两个班竞赛成绩的平均数和中位数,你认为哪个班的竞赛成绩较好;
(3)计算两个班竞赛成绩的方差,并说明哪个班的竞赛成绩较为整齐.
24.甲、乙两名队员参加射击训练,每次射击的环数均为整数.其成绩分别被制成如下统计图表(乙队员射击训练成绩统计图部分被污染):
平均成绩/环
中位数/环
众数/环
方差/环2
甲
7
7
12
乙
7
8
根据以上信息,解决下列问题:
(1)求出的值;
(2)直接写出乙队员第7次的射击环数及的值,并求出的值;
(3)若要选派其中一名参赛,你认为应选哪名队员?请说明你的理由.
25.拉尼娜现象再次到来,2020—2021或成超级寒冬,穿羽绒服是人们防寒保暧的常见方式.某羽绒服制造厂为了更好,更均匀地填充羽绒,准备新购进一种填充机器.现有甲、乙两种机器填充的标准质量均为200g
羽绒,工厂的采购员对甲、乙两种机器填充的若干羽绒服进行了抽样调查,对数据进行分类整理分析(羽绒质量用x表示,共分成四组A:,B:,C:,D:)并给出了下列信息:
从甲、乙两种机器填充的羽绒服中各自随机抽取10件,测得实际质量x(单位:g)如下:甲机器填充羽绒服中B组的数据是:196,198,198,198
乙机器填充羽绒的数据:200,196,205,197,204,199,203,200,200,198
甲机器填充羽绒的质量数据扇形统计图
甲、乙机器填充羽绒质量数据分析表
填充电器
甲
乙
平均数
中位数
b
200
众数
198
c
方差
请回答下列问题:
(1)________,_________,_________.
(2)请根据以上数据判断羽绒填充机情况比较好的是_________(填甲或乙)说明你的理由.
(3)若甲、乙两种机器填充的这批羽绒服各有600件,估计这批羽绒服的质量属于C类的数量共有多少件?
26.疫情防控人人有责,为此我校在七、八年级举行了“新冠疫情防控”知识竞赛,从七、八年级各随机抽取了10名学生进行比赛(百分制),测试成绩整埋、描述和分析如下:
成绩得分用x表示,共分成四组:A.,B.,C.,D..
七年级10名学生的成绩是:96,80,96,86,99,96,90,100,89,82.
八年级10名学生的成绩在C组中的数据是:94,90,92.
七、八年级抽取的学生成绩统计表
年级
平均数
中位数
众数
方差
七年级
92
52
八年级
92
93
100
50.4
八年级抽取的学生成缵扇形统计图
根据以上信息,解答下列问题:
(1)这次比赛中_________年级成绩更平衡,更稳定;
(2)直接写出上述、、的值;_________,_________,_________.
(3)我校八年级共1200人参加了此次调查活动,估计参加此次调查活动成绩优秀()的学生人数是多少?试卷第2页,总2页
试卷第1页,总1页
苏教版九上数据的集中趋势和离散程度单元测试参考答案
1-10:CAABC
DDBDB
11.90
2
12.144
13.5
14.10
15.-3或7
16.8
17.乙
18.甲
19.(1)①1.4+0.8+0.4+1+2.4=6
②4.5
③
(2)选美团,平均数一样,中位数,众数美团均大于滴滴,且美团方差小,更稳定
20.解:(1)极差=48-36=12;
平均数=;
将48,36,42,36,36,42按从小到大的顺序排列为36,36,36,42,42,48,处于最中间位置的是36和42,故中位数=;
出现次数最多的为36,故众数为36;
所以表格如下:
极差
平均数
中位数
众数
12
40
39
36
故答案为:12,40,39,36;
(2)设平均每道工序筛选的损耗率是x,
根据题意得,1000×90%×40(1﹣x)2=23040,
解得:x=0.2,
答:平均每道工序筛选的损耗率是20%.
21.
(1),
因为甲中8共出现3次,次数最多,所以b=8
因为乙的有效次数中按顺序排列后处于中间位置的是9,所以中位数c=9;
故答案为a、b、c的值分别是8、8、9;
(2),
∴甲的方差较小,成绩比较稳定,
∴选择甲同学代表班级参加年级引体向上比赛;
∵乙的中位数是9,众数也是9,
∴获奖可能性较大,
∴根据去年比赛的成绩(至少9次才能获奖),决定选择乙同学代表班级参加年级引体向上比赛;
(3)∵原来的平均数是8,增加一次也是8,
∴平均数不变.
∵六次成绩排序为5,7,8,9,9,10,
∴处于中间位置的数为8,9,
∴中位数为
,
∴中位数变小.
后来的方差为,
∴方差变小.
22.(1)根据统计图知甲班70分的有6人且占总人数的30%,则甲班总人数为6÷30%=20人,甲班得80分的学生有3人,则得80分的学生占班级总人数的3÷20=15%,故得80分的学生所在扇形的圆心角度数为15%×360°=54°;根据班级总人数及得70分、80分、90分的人数即可求出得100分的学生人数为:20-6-3-6=5人;
故答案为54°,5人;
(2)将甲校的成绩从小到大排列后,处在第10、11位的两个学生的得分都是90分,因此平均分为=90,故中位数为90分;
故答案为90分;
(3)根据甲、乙两所学校参赛人数相等,故乙校总人数也为20人,可求乙校得80分的人数为:20-7-1-8=4(人),则乙校成绩的平均分为:(分);
故乙校的平均分为85分;
(4)∵<,
∴甲校的成绩离散程度较小,故甲校成绩比较稳定.
答:甲校的成绩比较稳定.
23.解:
(1)八(1)班的平均成绩是:(分)
八(2)班的平均成绩是:(分)
(2)八(1)班的中位数是分,八(2)班的中位数分;
两个班的平均成绩相同,八(2)班的中位数比八(1)班的中位数大,八(2)班的优秀学生多,
八(2)班的成绩优秀.
(3)八(1)班的方差为:
八(2)班的方差为:
八(1)班的成绩较为整齐.
24.解:(1)甲的平均成绩a=(环);
(2)∵已知的环数分别是:
3、4、6、7、8、8、9、10,平均数是7,
可知剩余两次的成绩和为:70-55=15(环),根据统计图可知不可能是9和6,只能是7和8,所以乙队员第7次的射击环数是7环或8环;
把乙的成绩从小到大排列:3、4、6、7、7、8、8、8、9、10,
∴乙射击成绩的中位数b==7.5(环),
其方差c=×[(3﹣7)2+(4﹣7)2+(6﹣7)2+2×(7﹣7)2+3×(8﹣7)2+(9﹣7)2+(10﹣7)2]
=×(16+9+1+3+4+9)
=4.2;
(3)从平均成绩看甲、乙二人的成绩相等均为7环,从中位数看甲射中7环以上的次数小于乙,从众数看甲射中7环的次数最多而乙射中8环的次数最多,从方差看乙的成绩比甲的成绩稳定;综合以上各因素,若选派一名队员参加比赛的话,可选择乙参赛,因为乙获得高分的可能更大.
25.(1),即,
甲机器中A组的数据有(个),所以甲机器中的中位数在第5个和第6个的数据都是198,所以;
乙机器填充羽绒的数据重新排列:196,197,198,199,200,200,200,203,204,205,
中位数在第5个和第6个的数据都是200,
200出现三次,最多,
∴乙机器中众数和中位数均是200,即;
∴,,;
(2)比较好的是乙;
乙的方差小,比较稳定;乙的众数为标准质量200g,而甲为198g;
(3),
∴属于C类的有480件.
26.解:(1)∵52>50.4,
∴这次比赛中八年级成绩更平衡,更稳定,
故答案为:八;
(2)a%=1-10%-20%-×100%=40%,则a=40;
七年级10名学生的成绩由小到大排列为:80,82,86,89,90,96,96,96,99,100,
∴b==93;
∵96出现的次数最多,
∴c=96;
故答案为:40,93,96;
(3)1200×40%=480人,
所以八年级参加此次调查活动成绩优秀的学生人数约为480人.
答案第1页,总2页
答案第1页,总2页
一、单选题(1-10题,每题3分,共30分)
1.一组数据4,2,x,3,9的平均数为4,则这组数据的众数和中位数分别是( )
A.3,2
B.2,2
C.2,3
D.2,4
2.面试时,某应聘者的学历、经验和工作态度的得分分别是72分、86分、60分,若依次按照1:3:2的比例确定成绩,则该应聘者的最终成绩是(
)
A.75
B.72
C.70
D.65
3.下列说法正确的是( )
A.一组数据3,5,4,5,6,7的众数、中位数和平均数都是5
B.为了解某灯管的使用寿命,可以采用普查的方式进行
C.两组身高数据的方差分别是S2甲=0.01,S2乙=0.02,那么乙组的身高比较整齐
D.“清明时节雨纷纷”是必然事件
4.我校七年级举行大合唱比赛,六位评委给七年级一班的打分如下:(单位:分),则该班得分的平均分为(
)
A.9.45分
B.9.50分
C.9.55分
D.9.60分
5.某学习小组9名学生参加“数学竞赛”,他们的得分情况如下表:
人数(人)
1
3
4
1
分数(分)
80
85
90
95
那么这9名学生所得分数的众数和中位数分别是(
)
A.90,87.5
B.90,85
C.90,90
D.85,85
6.为了更好地迎接庐阳区排球比赛,某校积极准备,从全校学生中遴选出21名同学进行相应的排球训练,该训练队成员的身高如下表:
身高(cm)
170
172
175
178
180
182
185
人数(个)
2
4
5
2
4
3
1
则该校排球队21名同学身高的众数和中位数分别是(单位:cm)( )
A.185,178
B.178,175
C.175,178
D.175,175
7.某企业复工之后,举行了一个简单的技工比赛,参赛的五名选手在单位时间内加工零件的合格率分别为:94.3%
,96.1%
,
94.3%
,91.7%
,93.5%.关于这组数据,下列说法正确的是( )
A.平均数是93.96%
B.方差是0
C.中位数是93.5%
D.众数是94.3%
8.在某中学举行的演讲比赛中,八年级5名参赛选手的成绩如下表所示,请你根据表中提供的数据,计算出这5名选手成绩的方差为( )
A.2
B.6.8
C.34
D.93
9.下表记录了甲、乙、丙、丁四名射击运动员最近几次选拔赛成绩的平均数和方差.根据表中数据,要从中选择一名成绩好且又发挥稳定的运动员参加比赛,应选择(
)
甲
乙
丙
丁
平均数(环)
9.14
9.15
9.14
9.15
方差
6.6
6.8
6.7
6.6
A.甲
B.乙
C.丙
D.丁
10.某单位招聘一名员工,从专业知识、工作业绩、面试成绩三个方面进行考核(考核的满分均为100分)方面的权重比依次为2∶4∶4.小明经过考核后所得的分数依次为90,85,80分,那么小明考核的最后得分是(
)
A.80
B.84
C.87
D.90
二、填空题(11-18题,每题2分,共16分)
11.小明五次测试成绩为:91、89、88、90、92,则五次测试成绩平均数为_____,方差为________.
12.如图是小明家今年1月份至5月份的每月用电量的统计图,据此推断他家这五个月的月平均用电量是_____度.
13.某班五个兴趣小组的人数分别为4,4,5,x,6,已知这组数据的平均数是5,则这组数据的中位数是_____.
14.2010年4月14日青海省玉树县发生7.1级大地震后,杭州浦阳中学九年级(5)班的42名同学踊跃捐款.有20人每人捐5元、11人每人捐10元、10人每人捐20元、1人捐100元.在这次每人捐款的数值中,中位数是____
15.一组数据-1、2、5、x的极差为8,则
x=_________.
16.已知一组数据x1,x2,x3,x4的平均数是5,则数据x1+3,x2+3,x3+3,x4+3的平均数是____.
17.甲乙两台机床生产同一种零件,并且每天产量相等,在6天众每天生产零件中的次品数依次是:甲:3、0、0、2、0、1、;乙:1、0、2、1、0、2.则甲、乙两台机床中性能较稳定的是______.
18.甲、乙、丙三名射击手的20次测试的平均成绩都是8环,方差分别(环2),(环2),(环2),则成绩最稳定的是________.
三、解答题(共74分)
19.近年来网约车十分流行,初三某班学生对“美团”和“滴滴”两家网约车公司各10名司机月收入进行了一项抽样调查,司机月收入(单位:千元)如图所示:
根据以上信息,整理分析数据如下:
平均月收入/千元
中位数/千元
众数/千元
方差/千元2
“美团”
①______
6
6
1.2
“滴滴”
6
②____
4
③_____
(1)完成表格填空;
(2)若从两家公司中选择一家做网约车司机,你会选哪家公司,并说明理由.
20.某村深入贯彻落实习近平新时代中国特色社会主义思想,认真践行“绿水青山就是金山银山”理念.在外打工的王大叔返回家乡创业,承包了一座荒山,栽了1000棵小枣树,发现成活率均为90%,并已挂果.为了分析收成情况,他从这座山上随意采摘了6棵树上的小枣,每棵的产量(千克)如下:48
36
42
36
36
42
(1)这组数据的极差、平均数、中位数、众数如表所示:
极差
平均数
中位数
众数
(2)这座山的枣子采摘后全部被某加工厂收购去进行精加工,经过两道工序的加工筛选后,最后筛选到合格的枣子总量为23040千克,平均每道工序筛选的损耗率是多少?
21.某校八年级(1)班甲、乙两男生在5次引体向上测试中有效次数如下:
甲:8,8,7,8,9;乙:5,9,7,10,9;
甲乙两同学引体向上的平均数、众数、中位数、方差如下:
平均数
众数
中位数
方差
甲
8
b
8
0.4
乙
a
9
c
3.2
根据以上信息,回答下列问题:
(1)表格是a= ,b= ,c= .(填数值)
(2)体育老师根据这5次的成绩,决定选择甲同学代表班级参加年级引体向上比赛,选择甲的理由是
.班主任李老师根据去年比赛的成绩(至少9次才能获奖),决定选择乙同学代表班级参加年级引体向上比赛,选择乙的理由是
;
(3)如果乙同学再做一次引体向上,有效次数为8,那么乙同学6次引体向上成绩的平均数
,中位数
,方差
.(填“变大”、“变小”或“不变”)
22.某市团委举办“我的中国梦”为主题的知识竞赛,甲、乙两所学校参赛人数相等,比赛结束后,发现学生成绩分别为70分,80分,90分,100分,并根据统计数据绘制了如下不完整的统计图表:
(1)在图①中,“80分”所在扇形的圆心角度数为 ;在图②中,“100分”的有 人;
(2)甲校成绩的中位数为 ;
(3)求乙校成绩的平均分;
(4)经计算知S甲2=135,S乙2=175,请你根据这两个数据,对甲、乙两校成绩作出合理评价.
23.为加强抗击疫情的教育宣传,某中学开展防疫知识线上竞赛活动,八年级(1)、(2)班各选出5名选手参加竞赛,两个班各选出的名选手的竞赛成绩(满分为分)如图所示:
(1)请你计算两个班的平均成绩各是多少分;
(2)写出两个班竞赛成绩的中位数,结合两个班竞赛成绩的平均数和中位数,你认为哪个班的竞赛成绩较好;
(3)计算两个班竞赛成绩的方差,并说明哪个班的竞赛成绩较为整齐.
24.甲、乙两名队员参加射击训练,每次射击的环数均为整数.其成绩分别被制成如下统计图表(乙队员射击训练成绩统计图部分被污染):
平均成绩/环
中位数/环
众数/环
方差/环2
甲
7
7
12
乙
7
8
根据以上信息,解决下列问题:
(1)求出的值;
(2)直接写出乙队员第7次的射击环数及的值,并求出的值;
(3)若要选派其中一名参赛,你认为应选哪名队员?请说明你的理由.
25.拉尼娜现象再次到来,2020—2021或成超级寒冬,穿羽绒服是人们防寒保暧的常见方式.某羽绒服制造厂为了更好,更均匀地填充羽绒,准备新购进一种填充机器.现有甲、乙两种机器填充的标准质量均为200g
羽绒,工厂的采购员对甲、乙两种机器填充的若干羽绒服进行了抽样调查,对数据进行分类整理分析(羽绒质量用x表示,共分成四组A:,B:,C:,D:)并给出了下列信息:
从甲、乙两种机器填充的羽绒服中各自随机抽取10件,测得实际质量x(单位:g)如下:甲机器填充羽绒服中B组的数据是:196,198,198,198
乙机器填充羽绒的数据:200,196,205,197,204,199,203,200,200,198
甲机器填充羽绒的质量数据扇形统计图
甲、乙机器填充羽绒质量数据分析表
填充电器
甲
乙
平均数
中位数
b
200
众数
198
c
方差
请回答下列问题:
(1)________,_________,_________.
(2)请根据以上数据判断羽绒填充机情况比较好的是_________(填甲或乙)说明你的理由.
(3)若甲、乙两种机器填充的这批羽绒服各有600件,估计这批羽绒服的质量属于C类的数量共有多少件?
26.疫情防控人人有责,为此我校在七、八年级举行了“新冠疫情防控”知识竞赛,从七、八年级各随机抽取了10名学生进行比赛(百分制),测试成绩整埋、描述和分析如下:
成绩得分用x表示,共分成四组:A.,B.,C.,D..
七年级10名学生的成绩是:96,80,96,86,99,96,90,100,89,82.
八年级10名学生的成绩在C组中的数据是:94,90,92.
七、八年级抽取的学生成绩统计表
年级
平均数
中位数
众数
方差
七年级
92
52
八年级
92
93
100
50.4
八年级抽取的学生成缵扇形统计图
根据以上信息,解答下列问题:
(1)这次比赛中_________年级成绩更平衡,更稳定;
(2)直接写出上述、、的值;_________,_________,_________.
(3)我校八年级共1200人参加了此次调查活动,估计参加此次调查活动成绩优秀()的学生人数是多少?试卷第2页,总2页
试卷第1页,总1页
苏教版九上数据的集中趋势和离散程度单元测试参考答案
1-10:CAABC
DDBDB
11.90
2
12.144
13.5
14.10
15.-3或7
16.8
17.乙
18.甲
19.(1)①1.4+0.8+0.4+1+2.4=6
②4.5
③
(2)选美团,平均数一样,中位数,众数美团均大于滴滴,且美团方差小,更稳定
20.解:(1)极差=48-36=12;
平均数=;
将48,36,42,36,36,42按从小到大的顺序排列为36,36,36,42,42,48,处于最中间位置的是36和42,故中位数=;
出现次数最多的为36,故众数为36;
所以表格如下:
极差
平均数
中位数
众数
12
40
39
36
故答案为:12,40,39,36;
(2)设平均每道工序筛选的损耗率是x,
根据题意得,1000×90%×40(1﹣x)2=23040,
解得:x=0.2,
答:平均每道工序筛选的损耗率是20%.
21.
(1),
因为甲中8共出现3次,次数最多,所以b=8
因为乙的有效次数中按顺序排列后处于中间位置的是9,所以中位数c=9;
故答案为a、b、c的值分别是8、8、9;
(2),
∴甲的方差较小,成绩比较稳定,
∴选择甲同学代表班级参加年级引体向上比赛;
∵乙的中位数是9,众数也是9,
∴获奖可能性较大,
∴根据去年比赛的成绩(至少9次才能获奖),决定选择乙同学代表班级参加年级引体向上比赛;
(3)∵原来的平均数是8,增加一次也是8,
∴平均数不变.
∵六次成绩排序为5,7,8,9,9,10,
∴处于中间位置的数为8,9,
∴中位数为
,
∴中位数变小.
后来的方差为,
∴方差变小.
22.(1)根据统计图知甲班70分的有6人且占总人数的30%,则甲班总人数为6÷30%=20人,甲班得80分的学生有3人,则得80分的学生占班级总人数的3÷20=15%,故得80分的学生所在扇形的圆心角度数为15%×360°=54°;根据班级总人数及得70分、80分、90分的人数即可求出得100分的学生人数为:20-6-3-6=5人;
故答案为54°,5人;
(2)将甲校的成绩从小到大排列后,处在第10、11位的两个学生的得分都是90分,因此平均分为=90,故中位数为90分;
故答案为90分;
(3)根据甲、乙两所学校参赛人数相等,故乙校总人数也为20人,可求乙校得80分的人数为:20-7-1-8=4(人),则乙校成绩的平均分为:(分);
故乙校的平均分为85分;
(4)∵<,
∴甲校的成绩离散程度较小,故甲校成绩比较稳定.
答:甲校的成绩比较稳定.
23.解:
(1)八(1)班的平均成绩是:(分)
八(2)班的平均成绩是:(分)
(2)八(1)班的中位数是分,八(2)班的中位数分;
两个班的平均成绩相同,八(2)班的中位数比八(1)班的中位数大,八(2)班的优秀学生多,
八(2)班的成绩优秀.
(3)八(1)班的方差为:
八(2)班的方差为:
八(1)班的成绩较为整齐.
24.解:(1)甲的平均成绩a=(环);
(2)∵已知的环数分别是:
3、4、6、7、8、8、9、10,平均数是7,
可知剩余两次的成绩和为:70-55=15(环),根据统计图可知不可能是9和6,只能是7和8,所以乙队员第7次的射击环数是7环或8环;
把乙的成绩从小到大排列:3、4、6、7、7、8、8、8、9、10,
∴乙射击成绩的中位数b==7.5(环),
其方差c=×[(3﹣7)2+(4﹣7)2+(6﹣7)2+2×(7﹣7)2+3×(8﹣7)2+(9﹣7)2+(10﹣7)2]
=×(16+9+1+3+4+9)
=4.2;
(3)从平均成绩看甲、乙二人的成绩相等均为7环,从中位数看甲射中7环以上的次数小于乙,从众数看甲射中7环的次数最多而乙射中8环的次数最多,从方差看乙的成绩比甲的成绩稳定;综合以上各因素,若选派一名队员参加比赛的话,可选择乙参赛,因为乙获得高分的可能更大.
25.(1),即,
甲机器中A组的数据有(个),所以甲机器中的中位数在第5个和第6个的数据都是198,所以;
乙机器填充羽绒的数据重新排列:196,197,198,199,200,200,200,203,204,205,
中位数在第5个和第6个的数据都是200,
200出现三次,最多,
∴乙机器中众数和中位数均是200,即;
∴,,;
(2)比较好的是乙;
乙的方差小,比较稳定;乙的众数为标准质量200g,而甲为198g;
(3),
∴属于C类的有480件.
26.解:(1)∵52>50.4,
∴这次比赛中八年级成绩更平衡,更稳定,
故答案为:八;
(2)a%=1-10%-20%-×100%=40%,则a=40;
七年级10名学生的成绩由小到大排列为:80,82,86,89,90,96,96,96,99,100,
∴b==93;
∵96出现的次数最多,
∴c=96;
故答案为:40,93,96;
(3)1200×40%=480人,
所以八年级参加此次调查活动成绩优秀的学生人数约为480人.
答案第1页,总2页
答案第1页,总2页
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
