11.2.2三角形的外角 同步练习-2021-2022学年人教版八年级数学上册(Word版含答案)
文档属性
| 名称 | 11.2.2三角形的外角 同步练习-2021-2022学年人教版八年级数学上册(Word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-31 00:00:00 | ||
图片预览





文档简介
11.2.2 三角形的外角
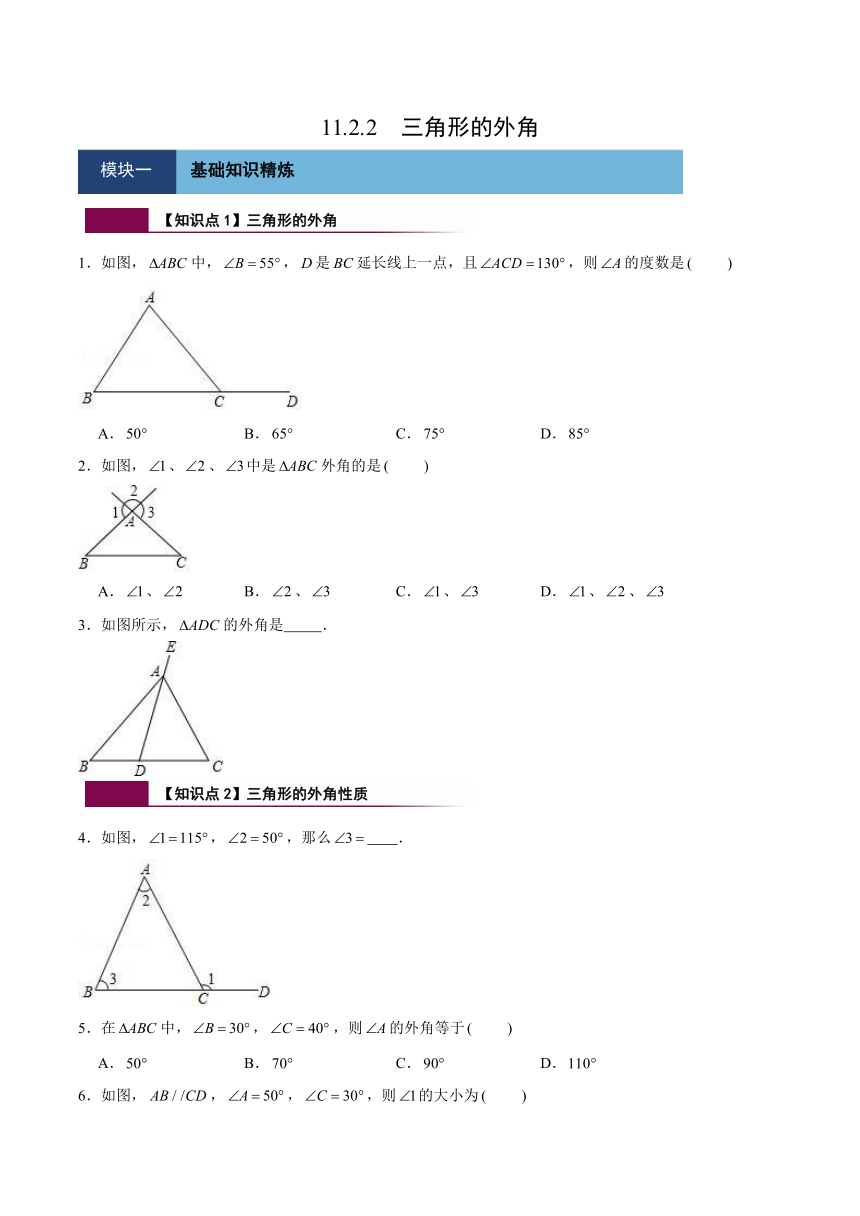
1.如图,中,,是延长线上一点,且,则的度数是
A.
B.
C.
D.
2.如图,、、中是外角的是
A.、
B.、
C.、
D.、、
3.如图所示,的外角是
.
4.如图,,,那么 .
5.在中,,,则的外角等于
A.
B.
C.
D.
6.如图,,,,则的大小为
A.
B.
C.
D.
7.将一副三角板按图中方式叠放,则的度数为
A.
B.
C.
D.
8.如图,点是内一点,连、,,,,则的度数是
A.
B.
C.
D.
9.一副三角板如图所示摆放,若,则的度数是
A.
B.
C.
D.
10.如图,、、的大小关系是
A
.
B
.
C
.
D
.
11.如图,是中的平分线,是的外角的平分线,如果,,则
A.
B.
C.
D.
12.如图,、的平分线、交于点,则与的数量关系为
A.
B.
C.
D.
13.如图,,、、分别平分的外角、内角、外角.以下结论:
①;②;③;④平分.
其中正确的结论有
A.1个
B.2个
C.3个
D.4个
14.如图所示,是的一个外角,
(1)若,,则
.
(2)若,,则
.
15.一副直角三角板如上图放置,点在的延长线上,,,,,则 .
16.如图,在中,,,是内一点,且,则的度数为 .
17.一个零件的形状如图所示,按规定应等于,,应分别是和.检验工人量得.就断定这个零件不合格,这是为什么?
18.互动学生课堂上,某小组同学对一个课题展开了探究.
小亮:已知,如图三角形,点是三角形内一点,连接,,试探究与、、之间的关系.
小明:可以用三角形内角和定理去解决.
小丽:用外角的相关结论也能解决.
(1)请你在横线上补全小明的探究过程:
,
,(等式性质)
,
,
.
(2)请你按照小丽的思路完成探究过程.
19.已知:如图,,点、分别在射线、上移动(不与点重合),平分,的反向延长线与的平分线相交于点.
(1)当时、的度数是多少?
(2)随着点、的移动,试问的大小是否变化?请说出你的理由.
20.如图①,在中,与的平分线相交于点.
(1)如果,求的度数;
(2)如图②,作外角、的平分线交于点,试探索、之间的数量关系.
(3)如图③,延长线段、交于点,中,存在一个内角等于另一个内角的3倍,请直接写出的度数.
参考答案
1.解:是的一个外角,
,
,
故选:.
2.解:属于外角的有、共2个.
故选:.
3.解:根据三角形的外角定义可知:
的外角为:,.
故答案为:,.
4.解:,,
,
故答案为:.
5.解:,,
的外角,
故选:.
6.,
,
;
故选:.
7.解:由题意得,,,
,
故选:.
8.解:延长交于,
是的一个外角,,,
,
是的一个外角
,
故选:.
9.如图,,,
,
,
故选:.
10.解:是三角形的一个外角,,
又是三角形的一个外角,,
.
故选:.
11.解:是中的平分线,是的外角的平分线,
,,
,,
,
,
,
,
,
,
故选:.
12.解:由三角形内角和定理得,,
,
、是、的平分线,
,,
,
,
故选:.
13.解:平分,
,
,,
,
,即①正确;
、分别平分、
,,
是的外角,
,即②正确;
平分,平分,
,,
,,,
,即③正确;
平分,
,
,,
不等于,即④错误;
正确的有3个,
故选:.
14.解:(1),,
.
(2),,
.
故答案为:52,52.
15.解:,,
,
,
,
,,
,
,
故答案为:15.
16.解:延长交于,
,
,
则,
,
,
,
故答案为:.
17.延长交于点,
因为工人量得,
所以,
又因为已知,
所以,
因为,
所以,
所以零件不合格.
18.解:(1),(三角形内角和定理)
,(等式性质)
,
,
(等量代换),
故答案为:三角形内角和定理;;;等量代换;
(2)如图,延长交于,
由三角形的外角性质可知,,,
.
19.解:(1),,
.
平分,
.
平分,
.
又,
.
(2)的大小不变,理由如下:
,平分,
.
平分,
.
又,
,
的大小不发生变化.
20.(1)解:.
,
点是和的平分线的交点,
,
(2)外角,的角平分线交于点,
;
(3)延长至,
为的外角的角平分线,
是的外角的平分线,
,
平分,
,
,
,
即,
又,
,即;
.
如果中,存在一个内角等于另一个内角的3倍,那么分四种情况:
①,则,;
②,则,,;
③,则,解得;
④,则,解得.
综上所述,的度数是或或或.
1.如图,中,,是延长线上一点,且,则的度数是
A.
B.
C.
D.
2.如图,、、中是外角的是
A.、
B.、
C.、
D.、、
3.如图所示,的外角是
.
4.如图,,,那么 .
5.在中,,,则的外角等于
A.
B.
C.
D.
6.如图,,,,则的大小为
A.
B.
C.
D.
7.将一副三角板按图中方式叠放,则的度数为
A.
B.
C.
D.
8.如图,点是内一点,连、,,,,则的度数是
A.
B.
C.
D.
9.一副三角板如图所示摆放,若,则的度数是
A.
B.
C.
D.
10.如图,、、的大小关系是
A
.
B
.
C
.
D
.
11.如图,是中的平分线,是的外角的平分线,如果,,则
A.
B.
C.
D.
12.如图,、的平分线、交于点,则与的数量关系为
A.
B.
C.
D.
13.如图,,、、分别平分的外角、内角、外角.以下结论:
①;②;③;④平分.
其中正确的结论有
A.1个
B.2个
C.3个
D.4个
14.如图所示,是的一个外角,
(1)若,,则
.
(2)若,,则
.
15.一副直角三角板如上图放置,点在的延长线上,,,,,则 .
16.如图,在中,,,是内一点,且,则的度数为 .
17.一个零件的形状如图所示,按规定应等于,,应分别是和.检验工人量得.就断定这个零件不合格,这是为什么?
18.互动学生课堂上,某小组同学对一个课题展开了探究.
小亮:已知,如图三角形,点是三角形内一点,连接,,试探究与、、之间的关系.
小明:可以用三角形内角和定理去解决.
小丽:用外角的相关结论也能解决.
(1)请你在横线上补全小明的探究过程:
,
,(等式性质)
,
,
.
(2)请你按照小丽的思路完成探究过程.
19.已知:如图,,点、分别在射线、上移动(不与点重合),平分,的反向延长线与的平分线相交于点.
(1)当时、的度数是多少?
(2)随着点、的移动,试问的大小是否变化?请说出你的理由.
20.如图①,在中,与的平分线相交于点.
(1)如果,求的度数;
(2)如图②,作外角、的平分线交于点,试探索、之间的数量关系.
(3)如图③,延长线段、交于点,中,存在一个内角等于另一个内角的3倍,请直接写出的度数.
参考答案
1.解:是的一个外角,
,
,
故选:.
2.解:属于外角的有、共2个.
故选:.
3.解:根据三角形的外角定义可知:
的外角为:,.
故答案为:,.
4.解:,,
,
故答案为:.
5.解:,,
的外角,
故选:.
6.,
,
;
故选:.
7.解:由题意得,,,
,
故选:.
8.解:延长交于,
是的一个外角,,,
,
是的一个外角
,
故选:.
9.如图,,,
,
,
故选:.
10.解:是三角形的一个外角,,
又是三角形的一个外角,,
.
故选:.
11.解:是中的平分线,是的外角的平分线,
,,
,,
,
,
,
,
,
,
故选:.
12.解:由三角形内角和定理得,,
,
、是、的平分线,
,,
,
,
故选:.
13.解:平分,
,
,,
,
,即①正确;
、分别平分、
,,
是的外角,
,即②正确;
平分,平分,
,,
,,,
,即③正确;
平分,
,
,,
不等于,即④错误;
正确的有3个,
故选:.
14.解:(1),,
.
(2),,
.
故答案为:52,52.
15.解:,,
,
,
,
,,
,
,
故答案为:15.
16.解:延长交于,
,
,
则,
,
,
,
故答案为:.
17.延长交于点,
因为工人量得,
所以,
又因为已知,
所以,
因为,
所以,
所以零件不合格.
18.解:(1),(三角形内角和定理)
,(等式性质)
,
,
(等量代换),
故答案为:三角形内角和定理;;;等量代换;
(2)如图,延长交于,
由三角形的外角性质可知,,,
.
19.解:(1),,
.
平分,
.
平分,
.
又,
.
(2)的大小不变,理由如下:
,平分,
.
平分,
.
又,
,
的大小不发生变化.
20.(1)解:.
,
点是和的平分线的交点,
,
(2)外角,的角平分线交于点,
;
(3)延长至,
为的外角的角平分线,
是的外角的平分线,
,
平分,
,
,
,
即,
又,
,即;
.
如果中,存在一个内角等于另一个内角的3倍,那么分四种情况:
①,则,;
②,则,,;
③,则,解得;
④,则,解得.
综上所述,的度数是或或或.
