11.3.2多边形的内角和 同步练习-2021-2022学年人教版八年级数学上册(Word版含答案)
文档属性
| 名称 | 11.3.2多边形的内角和 同步练习-2021-2022学年人教版八年级数学上册(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 567.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-31 17:22:57 | ||
图片预览

文档简介
11.3 多边形及其内角和
11.3.2 多边形的内角和
1.下面的多边形中,内角和是的是
A.
B.
C.
D.
2.如果一个多边形的内角和等于,则它的边数为
A.3
B.4
C.5
D.6
3.一个多边形的内角和是,这个多边形是
A.五边形
B.六边形
C.七边形
D.八边形
4.若一个正多边形的一个内角为,则这个图形为正 边形.
A.七
B.八
C.九
D.十
5.正六边形的外角和为
A.
B.
C.
D.
6.一个多边形的内角和是它的外角和的3倍,则这个多边形的边数是
A.10
B.8
C.6
D.5
7.正八边形中,每个内角与每个外角的度数之比为
A.
B.
C.
D.
8.一个边形的每一个外角都是,则等于
A.3
B.4
C.6
D.5
8.一个边形的每一个外角都是,则等于
A.3
B.4
C.6
D.5
9.一个正多边形的一个内角减去其外角为,则这个正多边形的边数是
A.八
B.九
C.十
D.十二
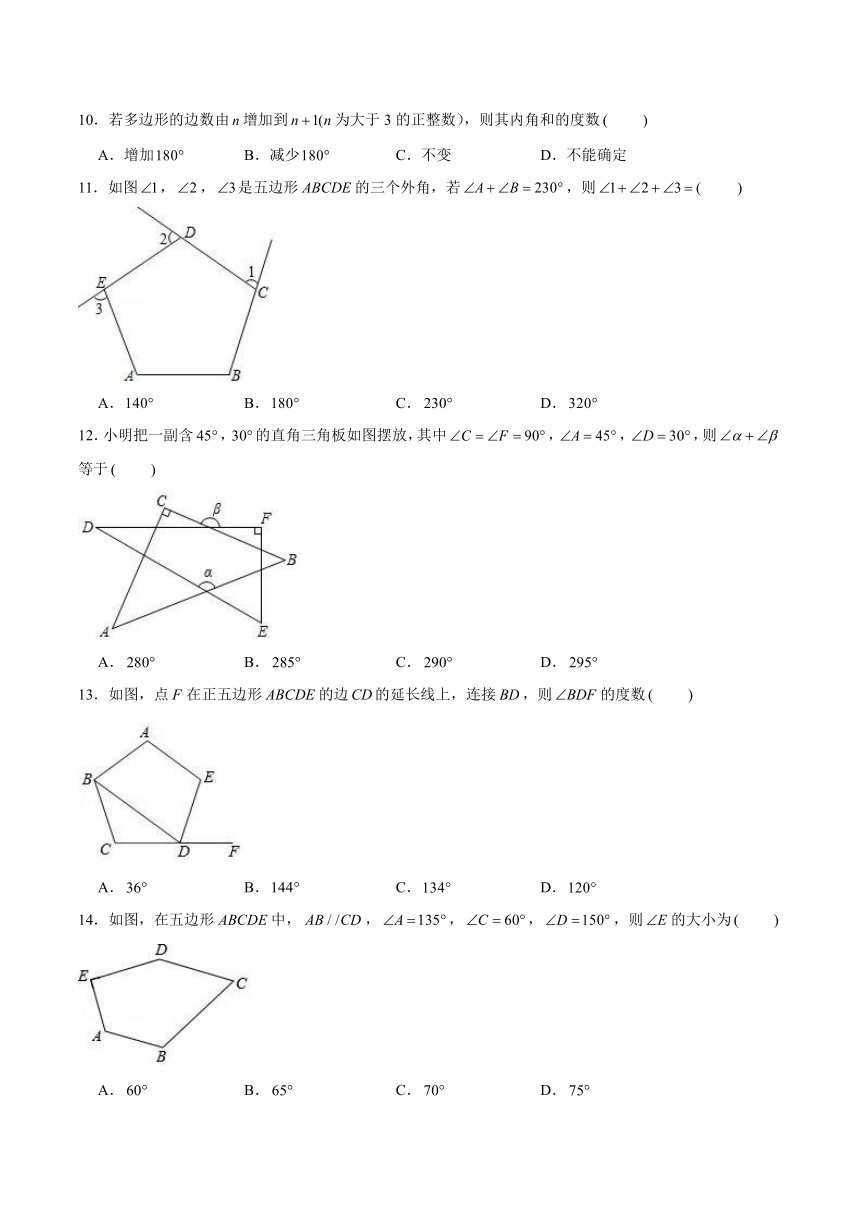
10.若多边形的边数由增加到为大于3的正整数),则其内角和的度数
A.增加
B.减少
C.不变
D.不能确定
11.如图,,是五边形的三个外角,若,则
A.
B.
C.
D.
12.小明把一副含,的直角三角板如图摆放,其中,,,则等于
A.
B.
C.
D.
13.如图,点在正五边形的边的延长线上,连接,则的度数
A.
B.
C.
D.
14.如图,在五边形中,,,,,则的大小为
A.
B.
C.
D.
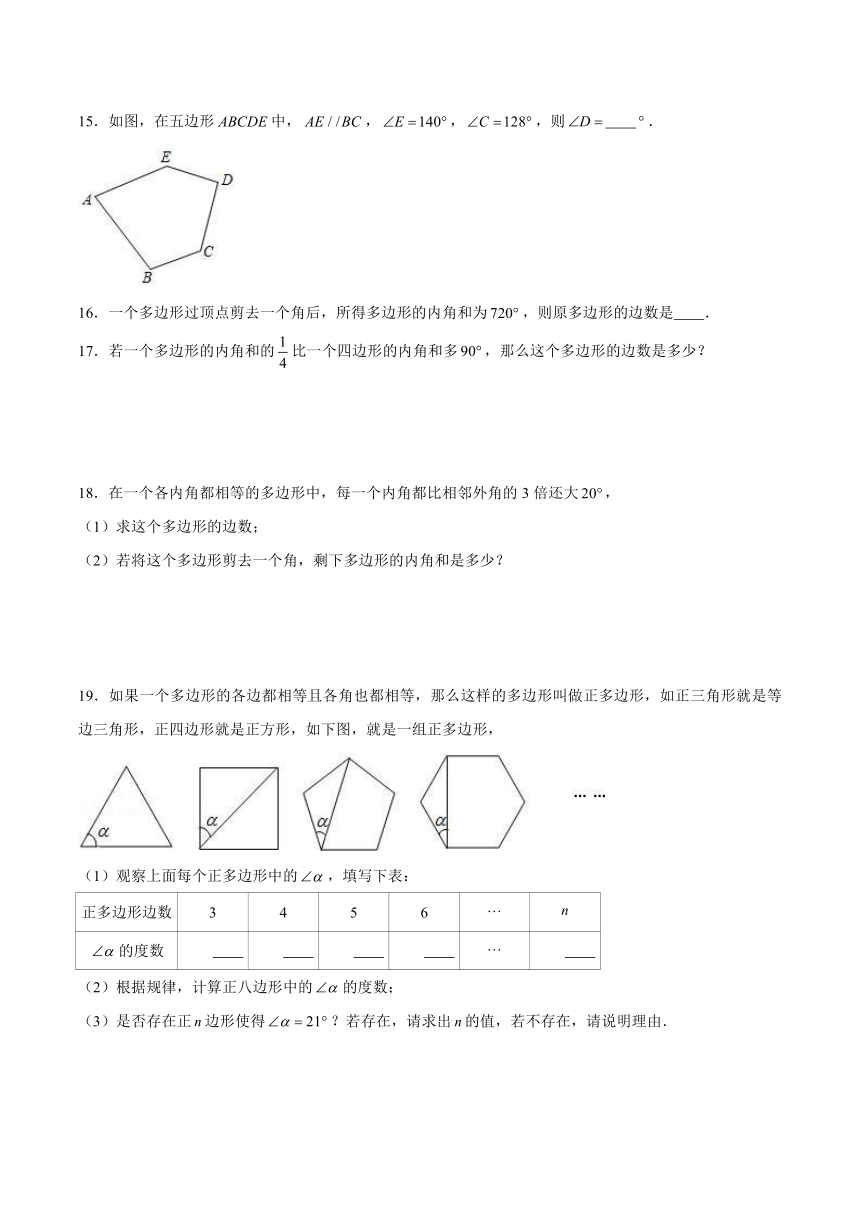
15.如图,在五边形中,,,,则 .
16.一个多边形过顶点剪去一个角后,所得多边形的内角和为,则原多边形的边数是 .
17.若一个多边形的内角和的比一个四边形的内角和多,那么这个多边形的边数是多少?
18.在一个各内角都相等的多边形中,每一个内角都比相邻外角的3倍还大,
(1)求这个多边形的边数;
(2)若将这个多边形剪去一个角,剩下多边形的内角和是多少?
19.如果一个多边形的各边都相等且各角也都相等,那么这样的多边形叫做正多边形,如正三角形就是等边三角形,正四边形就是正方形,如下图,就是一组正多边形,
(1)观察上面每个正多边形中的,填写下表:
正多边形边数
3
4
5
6
的度数
(2)根据规律,计算正八边形中的的度数;
(3)是否存在正边形使得?若存在,请求出的值,若不存在,请说明理由.
参考答案
1.解:边形的内角和公式为,
当,则.
四边形的内角和等于.
故选:.
2.解:设这个多边形的边数为,
,
.
故选:.
3.解:设这个多边形的边数为,由题意,得
,
解得:,
故这个多边形是六边形.
故选:.
4.解:设这个正多边形的边数为,
,
.
故选:.
5.解:正六边形的外角和是.
故选:.
6.解:设这个多边形是边形,由题意得:
,
解得:,
故选:.
7.解:这个八边形的内角和为:
;
这个八边形的每个内角的度数为:
;
这个八边形的每个外角的度数为:
;
这个八边形每个内角与每个外角的度数之比为:
.
故选:.
8.解:边形的每一个外角都是,
此边形是正边形,
,
故选:.
9.解:设内角为,则其外角为,由题意得:
,
解得:,
则其外角为,
这个正多边形的边数为:.
故选:.
10.解:边形的内角和是,边形的内角和是,则,
故选:.
11.解:五边形,,
,
又,
.
故选:.
12.解:
,,,
,
,,
,,
,
故选:.
13.解:五边形是正五边形,
,,
,
,
故选:.
14.解:,
,
五边形中,,,
.
故选:.
15.解:连接,
,
,
,,
,
,
故答案为:92.
16.解:设内角和为的多边形的边数是,则,
解得:.
多边形过顶点截去一个角后边数不变或减少1,
原多边形的边数为6或7,
故答案为:6或7.
17.解:设这个多边形的边数是,
由题意得:,
解得:,
答:这个多边形的边数是12.
18.解:(1)设多边形的一个外角为,则与其相邻的内角等于,
由题意,得,解得.
即多边形的每个外角为.
又多边形的外角和为,
多边形的外角个数.
多边形的边数,
答:这个多边形的边数是9;
(2)因为剪掉一个角以后,多边形的边数可能增加了1条,也可能减少了1条,或者不变,
当截线为经过对角2个顶点的直线时,多边形的边数减少了1条边,内角和;
当截线为经过多边形一组对边的直线时,多边形的边数不变,内角和;
当截线为只经过正方形一组邻边的一条直线时,多边形的边数增加一条边,内角和.
答:将这个多边形剪去一个角,剩下多边形的内角和是或或.
19.解:(1)观察上面每个正多边形中的,填写下表:
正多边形边数
3
4
5
6
的度数
(2)根据规律,计算正八边形中的;
(3)不存在,理由如下:
设存在正边形使得,
得.
解得,是正整数,(不符合题意要舍去),
不存在正边形使得.
11.3.2 多边形的内角和
1.下面的多边形中,内角和是的是
A.
B.
C.
D.
2.如果一个多边形的内角和等于,则它的边数为
A.3
B.4
C.5
D.6
3.一个多边形的内角和是,这个多边形是
A.五边形
B.六边形
C.七边形
D.八边形
4.若一个正多边形的一个内角为,则这个图形为正 边形.
A.七
B.八
C.九
D.十
5.正六边形的外角和为
A.
B.
C.
D.
6.一个多边形的内角和是它的外角和的3倍,则这个多边形的边数是
A.10
B.8
C.6
D.5
7.正八边形中,每个内角与每个外角的度数之比为
A.
B.
C.
D.
8.一个边形的每一个外角都是,则等于
A.3
B.4
C.6
D.5
8.一个边形的每一个外角都是,则等于
A.3
B.4
C.6
D.5
9.一个正多边形的一个内角减去其外角为,则这个正多边形的边数是
A.八
B.九
C.十
D.十二
10.若多边形的边数由增加到为大于3的正整数),则其内角和的度数
A.增加
B.减少
C.不变
D.不能确定
11.如图,,是五边形的三个外角,若,则
A.
B.
C.
D.
12.小明把一副含,的直角三角板如图摆放,其中,,,则等于
A.
B.
C.
D.
13.如图,点在正五边形的边的延长线上,连接,则的度数
A.
B.
C.
D.
14.如图,在五边形中,,,,,则的大小为
A.
B.
C.
D.
15.如图,在五边形中,,,,则 .
16.一个多边形过顶点剪去一个角后,所得多边形的内角和为,则原多边形的边数是 .
17.若一个多边形的内角和的比一个四边形的内角和多,那么这个多边形的边数是多少?
18.在一个各内角都相等的多边形中,每一个内角都比相邻外角的3倍还大,
(1)求这个多边形的边数;
(2)若将这个多边形剪去一个角,剩下多边形的内角和是多少?
19.如果一个多边形的各边都相等且各角也都相等,那么这样的多边形叫做正多边形,如正三角形就是等边三角形,正四边形就是正方形,如下图,就是一组正多边形,
(1)观察上面每个正多边形中的,填写下表:
正多边形边数
3
4
5
6
的度数
(2)根据规律,计算正八边形中的的度数;
(3)是否存在正边形使得?若存在,请求出的值,若不存在,请说明理由.
参考答案
1.解:边形的内角和公式为,
当,则.
四边形的内角和等于.
故选:.
2.解:设这个多边形的边数为,
,
.
故选:.
3.解:设这个多边形的边数为,由题意,得
,
解得:,
故这个多边形是六边形.
故选:.
4.解:设这个正多边形的边数为,
,
.
故选:.
5.解:正六边形的外角和是.
故选:.
6.解:设这个多边形是边形,由题意得:
,
解得:,
故选:.
7.解:这个八边形的内角和为:
;
这个八边形的每个内角的度数为:
;
这个八边形的每个外角的度数为:
;
这个八边形每个内角与每个外角的度数之比为:
.
故选:.
8.解:边形的每一个外角都是,
此边形是正边形,
,
故选:.
9.解:设内角为,则其外角为,由题意得:
,
解得:,
则其外角为,
这个正多边形的边数为:.
故选:.
10.解:边形的内角和是,边形的内角和是,则,
故选:.
11.解:五边形,,
,
又,
.
故选:.
12.解:
,,,
,
,,
,,
,
故选:.
13.解:五边形是正五边形,
,,
,
,
故选:.
14.解:,
,
五边形中,,,
.
故选:.
15.解:连接,
,
,
,,
,
,
故答案为:92.
16.解:设内角和为的多边形的边数是,则,
解得:.
多边形过顶点截去一个角后边数不变或减少1,
原多边形的边数为6或7,
故答案为:6或7.
17.解:设这个多边形的边数是,
由题意得:,
解得:,
答:这个多边形的边数是12.
18.解:(1)设多边形的一个外角为,则与其相邻的内角等于,
由题意,得,解得.
即多边形的每个外角为.
又多边形的外角和为,
多边形的外角个数.
多边形的边数,
答:这个多边形的边数是9;
(2)因为剪掉一个角以后,多边形的边数可能增加了1条,也可能减少了1条,或者不变,
当截线为经过对角2个顶点的直线时,多边形的边数减少了1条边,内角和;
当截线为经过多边形一组对边的直线时,多边形的边数不变,内角和;
当截线为只经过正方形一组邻边的一条直线时,多边形的边数增加一条边,内角和.
答:将这个多边形剪去一个角,剩下多边形的内角和是或或.
19.解:(1)观察上面每个正多边形中的,填写下表:
正多边形边数
3
4
5
6
的度数
(2)根据规律,计算正八边形中的;
(3)不存在,理由如下:
设存在正边形使得,
得.
解得,是正整数,(不符合题意要舍去),
不存在正边形使得.
