11.3.1多边形 同步练习-2021-2022学年人教版八年级数学上册(Word版含答案)
文档属性
| 名称 | 11.3.1多边形 同步练习-2021-2022学年人教版八年级数学上册(Word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 349.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-31 00:00:00 | ||
图片预览


文档简介
11.3 多边形及其内角和
11.3.1 多边形
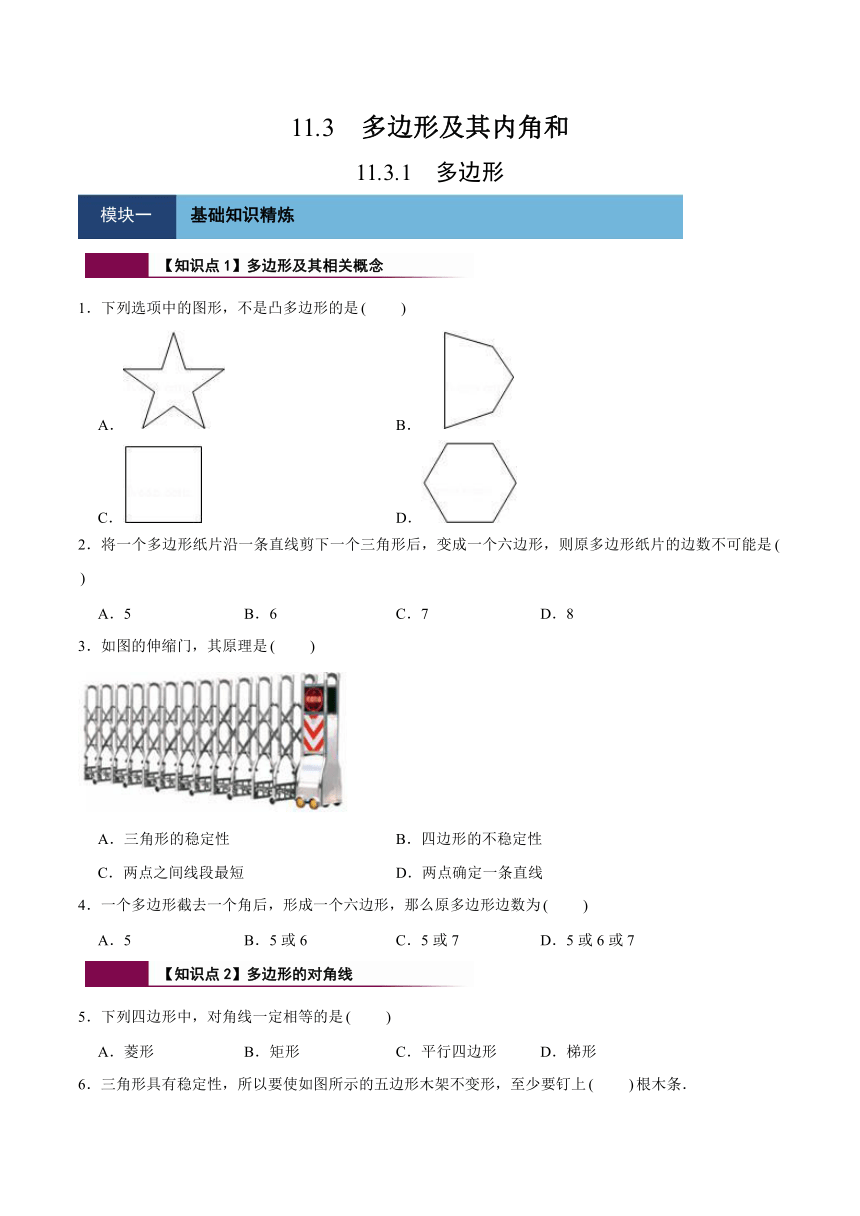
1.下列选项中的图形,不是凸多边形的是
A.
B.
C.
D.
2.将一个多边形纸片沿一条直线剪下一个三角形后,变成一个六边形,则原多边形纸片的边数不可能是
A.5
B.6
C.7
D.8
3.如图的伸缩门,其原理是
A.三角形的稳定性
B.四边形的不稳定性
C.两点之间线段最短
D.两点确定一条直线
4.一个多边形截去一个角后,形成一个六边形,那么原多边形边数为
A.5
B.5或6
C.5或7
D.5或6或7
5.下列四边形中,对角线一定相等的是
A.菱形
B.矩形
C.平行四边形
D.梯形
6.三角形具有稳定性,所以要使如图所示的五边形木架不变形,至少要钉上 根木条.
A.1
B.2
C.3
D.4
7.从多边形一条边上的一点(不是顶点)出发,连接各个顶点得到2003个三角形,则这个多边形的边数为
A.2001
B.2005
C.2004
D.2006
8.从一个七边形的某个顶点出发,分别连接这个点与其余各顶点,可以把一个七边形分割成 个三角形.
A.6
B.5
C.8
D.7
9.下列图形为正多边形的是
A.
B.
C.
D.
10.四边相等的四边形是
A.菱形
B.矩形
C.正方形
D.梯形
11.下列图形中,是正多边形的是
A.等腰三角形
B.长方形
C.正方形
D.五边都相等的五边形
12.对角线互相垂直平分的四边形是
A.菱形、正方形
B.矩形、菱形
C.矩形、正方形
D.平行四边形、菱形
13.在六边形内任取一点,
把这个点与六边形的各顶点分别连接可以得到
A
.
4
个三角形
B
.
5
个三角形
C
.
6
个三角形
D
.
7
个三角形
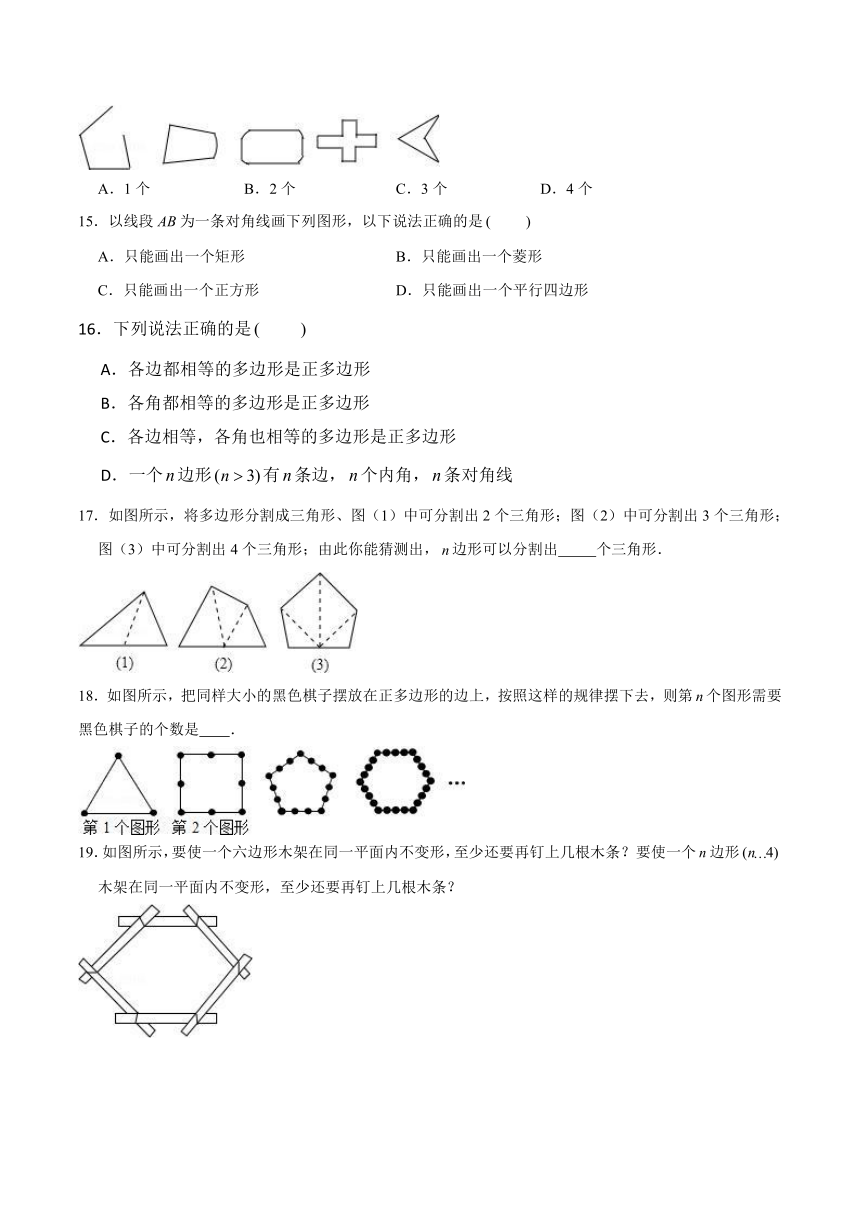
14.下列图形中,多边形有
A.1个
B.2个
C.3个
D.4个
15.以线段为一条对角线画下列图形,以下说法正确的是
A.只能画出一个矩形
B.只能画出一个菱形
C.只能画出一个正方形
D.只能画出一个平行四边形
16.下列说法正确的是
A.各边都相等的多边形是正多边形
B.各角都相等的多边形是正多边形
C.各边相等,各角也相等的多边形是正多边形
D.一个边形有条边,个内角,条对角线
17.如图所示,将多边形分割成三角形、图(1)中可分割出2个三角形;图(2)中可分割出3个三角形;图(3)中可分割出4个三角形;由此你能猜测出,边形可以分割出
个三角形.
18.如图所示,把同样大小的黑色棋子摆放在正多边形的边上,按照这样的规律摆下去,则第个图形需要黑色棋子的个数是 .
19.如图所示,要使一个六边形木架在同一平面内不变形,至少还要再钉上几根木条?要使一个边形木架在同一平面内不变形,至少还要再钉上几根木条?
参考答案
1.解:图形不是凸多边形的是.
故选:.
2.解:如图可知,原来多边形的边数可能是5,6,7.不可能是8.
故选:.
3.解:如图的伸缩门,其原理是四边形的不稳定性,
故选:.
4.解:如图可知,原来多边形的边数可能是5,6,7.
故选:.
5.解:菱形的对角线不一定相等,错误;
矩形的对角线一定相等,正确;
平行四边形的对角线不一定相等,错误;
梯形的对角线不一定相等,错误;
故选:.
6.解:过五边形的一个顶点作对角线,有条对角线,所以至少要钉上2根木条.
故选:.
7.解:多边形一条边上的一点(不是顶点)出发,连接各个顶点得到2003个三角形,
则这个多边形的边数为.
故选:.
8.解:从一个七边形的某个顶点出发,分别连接这个点与其余各顶点,可以把一个七边形分割成个三角形.
故选:.
9.解:正五边形五个角相等,五条边都相等,
故选:.
10.解:四边相等的四边形是菱形.
故选:.
11.解:正方形四个角相等,四条边都相等,
故选:.
12.解:对角线互相垂直平分的四边形是菱形或正方形,
故选:.
13.解:
在六边形内任取一点,
把这个点与六边形的各顶点分别连接可以得到六个三角形,
故选:.
14.解:由多边形的概念可知第四个、第五个是多边形共2个.
故选:.
15.解:矩形、菱形、正方形、平行四边形只有正方形的对角线与边的夹角是,为定值,
所以,以线段为一条对角线只能画出一个正方形.
故选:.
16.解:、各边都相等,各角都相等的多边形是正多边形,可得答案;
、各边都相等,各角都相等的多边形是正多边形,可得答案;
、各边都相等,各角都相等的多边形是正多边形,可得答案;
、一个边形有条边,个内角,条对角线,故错误;
故选:.
17.解:边形可以分割出个三角形.
18.解:第一个是,
第二个是,
第三个是,
第个是
故答案为:.
19.解:根据三角形的稳定性,要使六边形木架不变形,至少再钉上3根木条;
要使一个边形木架不变形,至少再钉上根木条.
11.3.1 多边形
1.下列选项中的图形,不是凸多边形的是
A.
B.
C.
D.
2.将一个多边形纸片沿一条直线剪下一个三角形后,变成一个六边形,则原多边形纸片的边数不可能是
A.5
B.6
C.7
D.8
3.如图的伸缩门,其原理是
A.三角形的稳定性
B.四边形的不稳定性
C.两点之间线段最短
D.两点确定一条直线
4.一个多边形截去一个角后,形成一个六边形,那么原多边形边数为
A.5
B.5或6
C.5或7
D.5或6或7
5.下列四边形中,对角线一定相等的是
A.菱形
B.矩形
C.平行四边形
D.梯形
6.三角形具有稳定性,所以要使如图所示的五边形木架不变形,至少要钉上 根木条.
A.1
B.2
C.3
D.4
7.从多边形一条边上的一点(不是顶点)出发,连接各个顶点得到2003个三角形,则这个多边形的边数为
A.2001
B.2005
C.2004
D.2006
8.从一个七边形的某个顶点出发,分别连接这个点与其余各顶点,可以把一个七边形分割成 个三角形.
A.6
B.5
C.8
D.7
9.下列图形为正多边形的是
A.
B.
C.
D.
10.四边相等的四边形是
A.菱形
B.矩形
C.正方形
D.梯形
11.下列图形中,是正多边形的是
A.等腰三角形
B.长方形
C.正方形
D.五边都相等的五边形
12.对角线互相垂直平分的四边形是
A.菱形、正方形
B.矩形、菱形
C.矩形、正方形
D.平行四边形、菱形
13.在六边形内任取一点,
把这个点与六边形的各顶点分别连接可以得到
A
.
4
个三角形
B
.
5
个三角形
C
.
6
个三角形
D
.
7
个三角形
14.下列图形中,多边形有
A.1个
B.2个
C.3个
D.4个
15.以线段为一条对角线画下列图形,以下说法正确的是
A.只能画出一个矩形
B.只能画出一个菱形
C.只能画出一个正方形
D.只能画出一个平行四边形
16.下列说法正确的是
A.各边都相等的多边形是正多边形
B.各角都相等的多边形是正多边形
C.各边相等,各角也相等的多边形是正多边形
D.一个边形有条边,个内角,条对角线
17.如图所示,将多边形分割成三角形、图(1)中可分割出2个三角形;图(2)中可分割出3个三角形;图(3)中可分割出4个三角形;由此你能猜测出,边形可以分割出
个三角形.
18.如图所示,把同样大小的黑色棋子摆放在正多边形的边上,按照这样的规律摆下去,则第个图形需要黑色棋子的个数是 .
19.如图所示,要使一个六边形木架在同一平面内不变形,至少还要再钉上几根木条?要使一个边形木架在同一平面内不变形,至少还要再钉上几根木条?
参考答案
1.解:图形不是凸多边形的是.
故选:.
2.解:如图可知,原来多边形的边数可能是5,6,7.不可能是8.
故选:.
3.解:如图的伸缩门,其原理是四边形的不稳定性,
故选:.
4.解:如图可知,原来多边形的边数可能是5,6,7.
故选:.
5.解:菱形的对角线不一定相等,错误;
矩形的对角线一定相等,正确;
平行四边形的对角线不一定相等,错误;
梯形的对角线不一定相等,错误;
故选:.
6.解:过五边形的一个顶点作对角线,有条对角线,所以至少要钉上2根木条.
故选:.
7.解:多边形一条边上的一点(不是顶点)出发,连接各个顶点得到2003个三角形,
则这个多边形的边数为.
故选:.
8.解:从一个七边形的某个顶点出发,分别连接这个点与其余各顶点,可以把一个七边形分割成个三角形.
故选:.
9.解:正五边形五个角相等,五条边都相等,
故选:.
10.解:四边相等的四边形是菱形.
故选:.
11.解:正方形四个角相等,四条边都相等,
故选:.
12.解:对角线互相垂直平分的四边形是菱形或正方形,
故选:.
13.解:
在六边形内任取一点,
把这个点与六边形的各顶点分别连接可以得到六个三角形,
故选:.
14.解:由多边形的概念可知第四个、第五个是多边形共2个.
故选:.
15.解:矩形、菱形、正方形、平行四边形只有正方形的对角线与边的夹角是,为定值,
所以,以线段为一条对角线只能画出一个正方形.
故选:.
16.解:、各边都相等,各角都相等的多边形是正多边形,可得答案;
、各边都相等,各角都相等的多边形是正多边形,可得答案;
、各边都相等,各角都相等的多边形是正多边形,可得答案;
、一个边形有条边,个内角,条对角线,故错误;
故选:.
17.解:边形可以分割出个三角形.
18.解:第一个是,
第二个是,
第三个是,
第个是
故答案为:.
19.解:根据三角形的稳定性,要使六边形木架不变形,至少再钉上3根木条;
要使一个边形木架不变形,至少再钉上根木条.
