第五章质量与密度专题训练 测量物体的密度 密度的相关计算 2021---2022学年沪科版八年级物理(含答案)
文档属性
| 名称 | 第五章质量与密度专题训练 测量物体的密度 密度的相关计算 2021---2022学年沪科版八年级物理(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 157.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-07-30 13:23:52 | ||
图片预览




文档简介
测量物体的密度
【实验报告】
一、测量固体的密度
1.实验原理:ρ=mV。
2.实验器材:天平、量筒、细线、烧杯。
3.实验步骤
(1)用天平测出物体的质量m;
(2)向量筒里倒适量的水,测出水的体积V1;
(3)用细线系住物体放入量筒,测出两者的体积之和V2。
4.密度计算式:ρ=?mV2?V1 。?
5.误差分析
(1)若先测质量,后测量体积,仪器本身及读数会引起测量误差(既有质量误差,也有体积误差),但误差主要来源于体积的测量,误差偏大或偏小是不确定的;
(2)若先测体积,后测量质量,物体会沾有一部分水,使得测出的质量 ,进而测出的密度也 ,这种测量顺序是不可取的。?
二、测量液体的密度
1.实验原理:ρ=mV。
2.实验器材:天平、量筒、烧杯。
3.实验步骤
(1)用天平测出烧杯和液体的总质量m1;
(2)将烧杯中的液体部分倒入量筒中,用天平测出剩下的液体和烧杯的总质量m2;
(3)读出量筒中液体的体积V。
4.密度计算式:ρ=?m1?m2V 。?
5.其他方法误差分析
(1)先测液体体积V,后测液体质量m,因量筒中有残留液体(体积无法读出),所测的液体质量并不是体积V对应的质量,则测出的质量偏小,测得的密度 ;?
(2)先测液体质量m,后测液体体积V,由于烧杯中的液体倒入量筒会有一部分残留,则测出的体积偏小,测得的密度 。?
【针对训练】
1.某物理兴趣小组为检测学校附近某条河的水质,需要测量河水的密度。取样后,他们利用天平和量筒进行了测量,实验过程如下:
【实验步骤】
(1)用已调平衡的天平测出空烧杯的质量m1为18 g;
(2)向烧杯中倒入适量的河水,测出烧杯和河水的总质量m2,如图甲所示;
(3)将烧杯中的河水全部倒入量筒中,读出量筒中河水的体积V,如图乙所示。
【实验数据处理】
在下表中填入上述实验数据及计算结果。
烧杯的质
量m1/g
烧杯与河水
的质量m2/g
河水的质
量m/g
河水的体
积V/cm3
河水的密度
ρ/(g·cm-3)
18
?
?
?
?
【实验评估】
按该实验方案测出的河水密度比实际值 (选填“偏大”或“偏小”)。?
2.[梧州中考改编]小明想测他最爱吃的李子的密度,于是进行了如下实验操作:
(1)调节天平平衡后,把一颗新鲜的李子放到天平的左盘上,当天平平衡时右盘添加的砝码数和游码位置如图甲所示,则李子的质量为 g;?
(2)小明不小心把量筒打碎了,老师建议他用一个质量为50 g的烧杯代替量筒继续做实验,他思考后,接受了老师的建议,进行了如下操作:
①往烧杯倒入适量的水,把李子放入烧杯中,发现李子沉入水中,如图乙所示,用油性笔在烧杯壁记下此时水面位置M;
②用天平测出杯、水和李子的总质量为112 g;
③将李子从水中取出,再往烧杯中缓慢加水,使水面上升至记号M,如图丙所示;
④用天平测出杯和水的总质量为110 g。
根据实验数据,计算出李子的体积为 cm3,密度为 g/cm3(ρ水=1.0×103kg/m3)。?
密度的相关计算
类型1 等体积问题
1.如图,一只烧杯盛满水时,称得其总质量为400 g;放入一金属球溢出一部分水后,称得其总质量为900 g;取出金属球后,称得烧杯和剩余水的质量为300 g(忽略金属球沾的水)。求此金属球的密度。
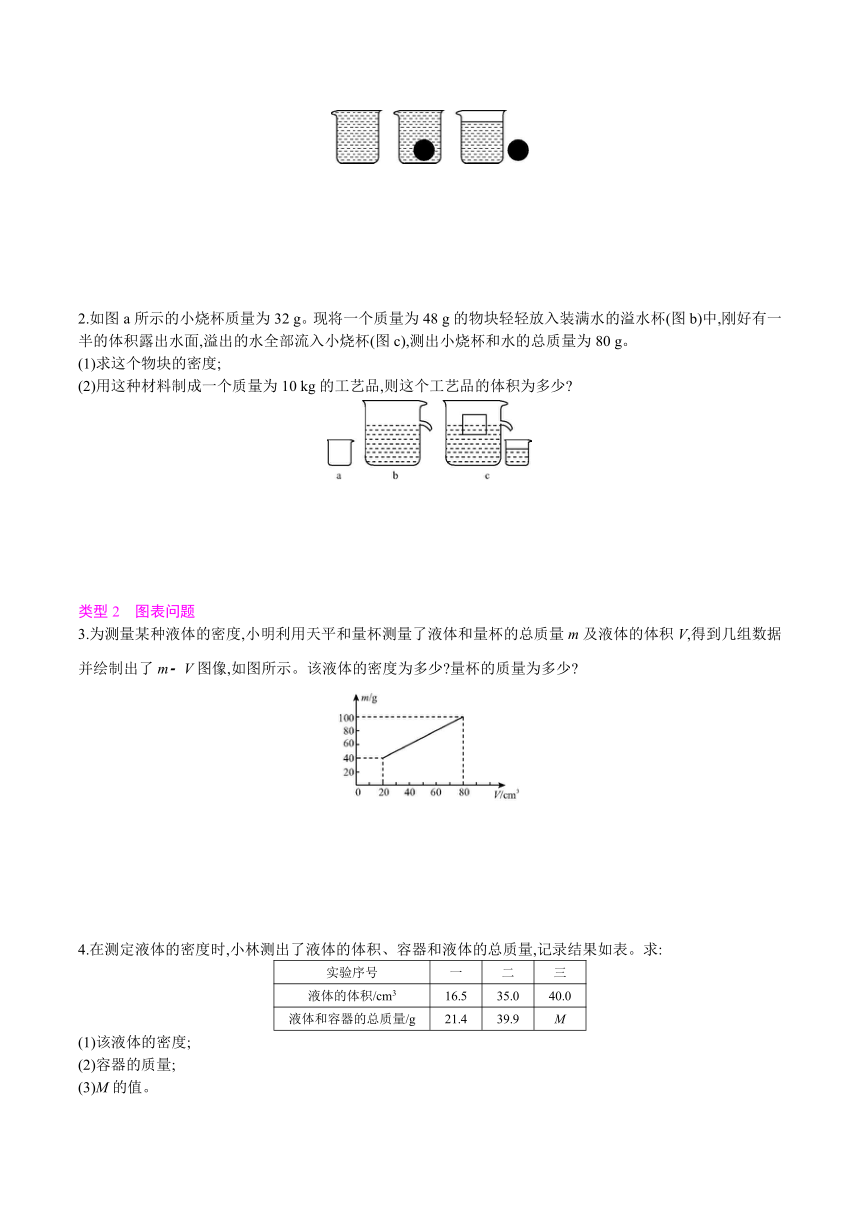
2.如图a所示的小烧杯质量为32 g。现将一个质量为48 g的物块轻轻放入装满水的溢水杯(图b)中,刚好有一半的体积露出水面,溢出的水全部流入小烧杯(图c),测出小烧杯和水的总质量为80 g。
(1)求这个物块的密度;
(2)用这种材料制成一个质量为10 kg的工艺品,则这个工艺品的体积为多少?
类型2 图表问题
3.为测量某种液体的密度,小明利用天平和量杯测量了液体和量杯的总质量m及液体的体积V,得到几组数据并绘制出了m?V图像,如图所示。该液体的密度为多少?量杯的质量为多少?
4.在测定液体的密度时,小林测出了液体的体积、容器和液体的总质量,记录结果如表。求:
实验序号
一
二
三
液体的体积/cm3
16.5
35.0
40.0
液体和容器的总质量/g
21.4
39.9
M
(1)该液体的密度;
(2)容器的质量;
(3)M的值。
类型3 凑整问题
5.如图所示,一个容积V0 =500 cm3、质量m0 = 0.5 kg的瓶子里装有水。乌鸦为了喝到瓶子里的水,就衔了很多的小石块放到瓶子里,让水面上升到瓶口。若瓶内有质量m1 =0.4 kg的水(水的密度ρ水=1.0×103 kg/m3 ,石块密度ρ石 =2.6×103 kg/m3 )。求:
(1)瓶中水的体积V1 ;
(2)乌鸦投入瓶子中的石块的体积V2 ;
(3)乌鸦投入石块后,瓶子、石块和水的总质量m。
6.小华在家中发现一金属块,学习密度知识后,他做了如下实验:先用电子秤测出一个空玻璃瓶的质量为200 g,再装满水,测得总质量为700 g。将水倒出,烘干玻璃瓶,将金属块缓慢放入玻璃瓶中,测得玻璃瓶和金属块总质量为2200 g,然后再向玻璃瓶中加水至满,测出三者总质量为2500 g。求:
(1)玻璃瓶的容积;
(2)金属块的质量;
(3)金属块的密度。
类型4 空心问题
7.为判断一个铝球是否是实心的,小张对铝球进行了测量,实验数据如下(ρ铝=2.7×103 kg/m3,ρ水=1.0×103 kg/m3):
铝球的质量m/g
水的体积V1/mL
水和铝球的
总体积V2/mL
27
50.0
65.0
(1)该铝球是空心还是实心的?(根据计算结果说明)
(2)若铝球是空心的,空心部分的体积是多大?
(3)若在空心部分注满水,水的质量是多少?
类型5 混合密度问题
8.王慧同学利用所学知识,测量一件用合金制成的实心构件中铝所占的比例。她首先用天平测出构件的质量为374 g,用量杯测出构件的体积是100 cm3。已知合金由铝与钢两种材料合成,且铝的密度为2.7×103 kg/m3,钢的密度为7.9×103 kg/m3。如果构件的体积等于原来两种金属体积之和。求:
(1)这种合金的平均密度;
(2)这种合金中铝的质量占总质量的百分比。
测量物体的密度
【实验报告】
一、测量固体的密度
1.实验原理:ρ=mV。
2.实验器材:天平、量筒、细线、烧杯。
3.实验步骤
(1)用天平测出物体的质量m;
(2)向量筒里倒适量的水,测出水的体积V1;
(3)用细线系住物体放入量筒,测出两者的体积之和V2。
4.密度计算式:ρ=?mV2?V1 。?
5.误差分析
(1)若先测质量,后测量体积,仪器本身及读数会引起测量误差(既有质量误差,也有体积误差),但误差主要来源于体积的测量,误差偏大或偏小是不确定的;
(2)若先测体积,后测量质量,物体会沾有一部分水,使得测出的质量 偏大 ,进而测出的密度也 偏大 ,这种测量顺序是不可取的。?
二、测量液体的密度
1.实验原理:ρ=mV。
2.实验器材:天平、量筒、烧杯。
3.实验步骤
(1)用天平测出烧杯和液体的总质量m1;
(2)将烧杯中的液体部分倒入量筒中,用天平测出剩下的液体和烧杯的总质量m2;
(3)读出量筒中液体的体积V。
4.密度计算式:ρ=?m1?m2V 。?
5.其他方法误差分析
(1)先测液体体积V,后测液体质量m,因量筒中有残留液体(体积无法读出),所测的液体质量并不是体积V对应的质量,则测出的质量偏小,测得的密度 偏小 ;?
(2)先测液体质量m,后测液体体积V,由于烧杯中的液体倒入量筒会有一部分残留,则测出的体积偏小,测得的密度 偏大 。?
【针对训练】
1.某物理兴趣小组为检测学校附近某条河的水质,需要测量河水的密度。取样后,他们利用天平和量筒进行了测量,实验过程如下:
【实验步骤】
(1)用已调平衡的天平测出空烧杯的质量m1为18 g;
(2)向烧杯中倒入适量的河水,测出烧杯和河水的总质量m2,如图甲所示;
(3)将烧杯中的河水全部倒入量筒中,读出量筒中河水的体积V,如图乙所示。
【实验数据处理】
在下表中填入上述实验数据及计算结果。
烧杯的质
量m1/g
烧杯与河水
的质量m2/g
河水的质
量m/g
河水的体
积V/cm3
河水的密度
ρ/(g·cm-3)
18
49 ?
31 ?
30 ?
1.03 ?
【实验评估】
按该实验方案测出的河水密度比实际值 偏大 (选填“偏大”或“偏小”)。?
2.[梧州中考改编]小明想测他最爱吃的李子的密度,于是进行了如下实验操作:
(1)调节天平平衡后,把一颗新鲜的李子放到天平的左盘上,当天平平衡时右盘添加的砝码数和游码位置如图甲所示,则李子的质量为 12 g;?
(2)小明不小心把量筒打碎了,老师建议他用一个质量为50 g的烧杯代替量筒继续做实验,他思考后,接受了老师的建议,进行了如下操作:
①往烧杯倒入适量的水,把李子放入烧杯中,发现李子沉入水中,如图乙所示,用油性笔在烧杯壁记下此时水面位置M;
②用天平测出杯、水和李子的总质量为112 g;
③将李子从水中取出,再往烧杯中缓慢加水,使水面上升至记号M,如图丙所示;
④用天平测出杯和水的总质量为110 g。
根据实验数据,计算出李子的体积为 10 cm3,密度为 1.2 g/cm3(ρ水=1.0×103kg/m3)。?
密度的相关计算
类型1 等体积问题
1.如图,一只烧杯盛满水时,称得其总质量为400 g;放入一金属球溢出一部分水后,称得其总质量为900 g;取出金属球后,称得烧杯和剩余水的质量为300 g(忽略金属球沾的水)。求此金属球的密度。
解:溢出水的质量
m溢=m总-m剩=400 g-300 g=100 g
金属球的体积
V球=V溢=m溢ρ水=100 g1.0 g/cm3=100 cm3
金属球的质量
m=m1-m剩=900 g-300 g=600 g
金属球的密度
ρ=mV球=600 g100 cm3=6 g/cm3
2.如图a所示的小烧杯质量为32 g。现将一个质量为48 g的物块轻轻放入装满水的溢水杯(图b)中,刚好有一半的体积露出水面,溢出的水全部流入小烧杯(图c),测出小烧杯和水的总质量为80 g。
(1)求这个物块的密度;
(2)用这种材料制成一个质量为10 kg的工艺品,则这个工艺品的体积为多少?
解:(1)由题意知,物块浸入水中的体积等于它排开水的体积,即
V浸=V排=m水ρ水=m总?m1ρ水=80 g?32 g1.0 g/cm3=48 cm3
由题意知,物块的体积
V物=2V浸=2×48 cm3=96 cm3
则物块的密度为
ρ物=m物V物=48 g96 cm3=0.5 g/cm3=0.5×103 kg/m3
(2)这个工艺品的体积为
V'物=m' 物ρ物=10 kg0.5×103kg/m3=0.02 m3
类型2 图表问题
3.为测量某种液体的密度,小明利用天平和量杯测量了液体和量杯的总质量m及液体的体积V,得到几组数据并绘制出了m?V图像,如图所示。该液体的密度为多少?量杯的质量为多少?
解:设量杯的质量为m杯,液体的密度为ρ,由题图可知,当液体体积为V1=20 cm3时,液体和量杯的总质量m总1=m1+m杯=40 g
则ρ×20 cm3+m杯=40 g ①
当液体体积为V2=80 cm3时,液体和量杯的总质量m总2=m2+m杯=100 g
则ρ×80 cm3+m杯=100 g ②
联立①②,解得液体的密度ρ=1 g/cm3,m杯=20 g
4.在测定液体的密度时,小林测出了液体的体积、容器和液体的总质量,记录结果如表。求:
实验序号
一
二
三
液体的体积/cm3
16.5
35.0
40.0
液体和容器的总质量/g
21.4
39.9
M
(1)该液体的密度;
(2)容器的质量;
(3)M的值。
解:(1)第一次实验与第二次实验相比,液体体积的变化量
ΔV=35.0 cm3-16.5 cm3=18.5 cm3
液体和容器的总质量的变化量
Δm=39.9 g-21.4 g=18.5 g
该液体的密度
ρ=ΔmΔV=18.5 g18.5 cm3=1 g/cm3
(2)第一次实验时液体的质量
m1=ρV1=1 g/cm3×16.5 cm3=16.5 g
容器的质量
m容=m总1-m1=21.4 g-16.5 g=4.9 g
(3)第三次实验时液体的质量
m3=ρV3=1 g/cm3×40.0 cm3=40.0 g
液体和容器的总质量
m总3=m3+m容=40.0 g+4.9 g=44.9 g
即M=44.9
类型3 凑整问题
5.如图所示,一个容积V0 =500 cm3、质量m0 = 0.5 kg的瓶子里装有水。乌鸦为了喝到瓶子里的水,就衔了很多的小石块放到瓶子里,让水面上升到瓶口。若瓶内有质量m1 =0.4 kg的水(水的密度ρ水=1.0×103 kg/m3 ,石块密度ρ石 =2.6×103 kg/m3 )。求:
(1)瓶中水的体积V1 ;
(2)乌鸦投入瓶子中的石块的体积V2 ;
(3)乌鸦投入石块后,瓶子、石块和水的总质量m。
解:(1)瓶中水的体积
V1=m1ρ水=0.4 kg1.0×103kg/m3=4×10-4 m3=400 cm3
(2)瓶子中的石块的体积
V2=V0-V1=500 cm3-400 cm3=100 cm3
(3)石块的质量
m石=ρ石V2=2.6 g/cm3×100 cm3=260 g=0.26 kg
乌鸦投入石块后,瓶子、石块和水的总质量
m=m1+m0+m石=0.4 kg+0.5 kg+0.26 kg=1.16 kg
6.小华在家中发现一金属块,学习密度知识后,他做了如下实验:先用电子秤测出一个空玻璃瓶的质量为200 g,再装满水,测得总质量为700 g。将水倒出,烘干玻璃瓶,将金属块缓慢放入玻璃瓶中,测得玻璃瓶和金属块总质量为2200 g,然后再向玻璃瓶中加水至满,测出三者总质量为2500 g。求:
(1)玻璃瓶的容积;
(2)金属块的质量;
(3)金属块的密度。
解:(1)一满瓶水的质量为m水=m1-m0=700 g-200 g=500 g
由公式ρ=mV得,玻璃瓶的容积V瓶=V水=m水ρ水=500 g1 g/cm3=500 cm3
(2)金属块的质量为m金=m2-m0=2200 g-200 g=2000 g
(3)第2次向玻璃瓶中加入水的质量为Δm=2500 g-2200 g=300 g
这些水的体积为ΔV=Δmρ水=300 g1 g/ cm3=300 cm3
金属块的体积为V金=V瓶-ΔV=500 cm3-300 cm3=200 cm3
金属块的密度为ρ金=m金V金=2000 g200 cm3=10 g/cm3=1.0×104 kg/m3
类型4 空心问题
7.为判断一个铝球是否是实心的,小张对铝球进行了测量,实验数据如下(ρ铝=2.7×103 kg/m3,ρ水=1.0×103 kg/m3):
铝球的质量m/g
水的体积V1/mL
水和铝球的
总体积V2/mL
27
50.0
65.0
(1)该铝球是空心还是实心的?(根据计算结果说明)
(2)若铝球是空心的,空心部分的体积是多大?
(3)若在空心部分注满水,水的质量是多少?
解:(1)由ρ=mV可得,铝球中铝的体积
V铝=mρ铝=27 g2.7 g/cm3=10 cm3
因为V球=V2-V1=65.0 mL-50.0 mL=15.0 mL=15.0 cm3>10 cm3
所以该球是空心的。
(2)空心部分的体积
V空=V球-V铝=15 cm3-10 cm3=5 cm3
(3)在空心部分注满水后水的体积
V水=V空=5 cm3
由ρ=mV可得,水的质量
m水=ρ水V水=1.0 g/cm3×5 cm3=5 g
类型5 混合密度问题
8.王慧同学利用所学知识,测量一件用合金制成的实心构件中铝所占的比例。她首先用天平测出构件的质量为374 g,用量杯测出构件的体积是100 cm3。已知合金由铝与钢两种材料合成,且铝的密度为2.7×103 kg/m3,钢的密度为7.9×103 kg/m3。如果构件的体积等于原来两种金属体积之和。求:
(1)这种合金的平均密度;
(2)这种合金中铝的质量占总质量的百分比。
解:(1)这种合金的平均密度
ρ=mV=374 g100 cm3=3.74 g/cm3=3.74×103 kg/m3
(2)设铝的质量为m铝,钢的质量为m钢,则
m铝+m钢=374 g ①
由ρ=mV可得V=mρ,且构件的体积等于原来两种金属体积之和,则m铝ρ铝+m钢ρ钢=100 cm3
即m铝2.7 g/cm3+m钢7.9 g/cm3=100 cm3 ②
联立①②,解得m铝=216 g
则这种合金中铝的质量占总质量的百分比为216 g374 g×100%≈57.8%
【实验报告】
一、测量固体的密度
1.实验原理:ρ=mV。
2.实验器材:天平、量筒、细线、烧杯。
3.实验步骤
(1)用天平测出物体的质量m;
(2)向量筒里倒适量的水,测出水的体积V1;
(3)用细线系住物体放入量筒,测出两者的体积之和V2。
4.密度计算式:ρ=?mV2?V1 。?
5.误差分析
(1)若先测质量,后测量体积,仪器本身及读数会引起测量误差(既有质量误差,也有体积误差),但误差主要来源于体积的测量,误差偏大或偏小是不确定的;
(2)若先测体积,后测量质量,物体会沾有一部分水,使得测出的质量 ,进而测出的密度也 ,这种测量顺序是不可取的。?
二、测量液体的密度
1.实验原理:ρ=mV。
2.实验器材:天平、量筒、烧杯。
3.实验步骤
(1)用天平测出烧杯和液体的总质量m1;
(2)将烧杯中的液体部分倒入量筒中,用天平测出剩下的液体和烧杯的总质量m2;
(3)读出量筒中液体的体积V。
4.密度计算式:ρ=?m1?m2V 。?
5.其他方法误差分析
(1)先测液体体积V,后测液体质量m,因量筒中有残留液体(体积无法读出),所测的液体质量并不是体积V对应的质量,则测出的质量偏小,测得的密度 ;?
(2)先测液体质量m,后测液体体积V,由于烧杯中的液体倒入量筒会有一部分残留,则测出的体积偏小,测得的密度 。?
【针对训练】
1.某物理兴趣小组为检测学校附近某条河的水质,需要测量河水的密度。取样后,他们利用天平和量筒进行了测量,实验过程如下:
【实验步骤】
(1)用已调平衡的天平测出空烧杯的质量m1为18 g;
(2)向烧杯中倒入适量的河水,测出烧杯和河水的总质量m2,如图甲所示;
(3)将烧杯中的河水全部倒入量筒中,读出量筒中河水的体积V,如图乙所示。
【实验数据处理】
在下表中填入上述实验数据及计算结果。
烧杯的质
量m1/g
烧杯与河水
的质量m2/g
河水的质
量m/g
河水的体
积V/cm3
河水的密度
ρ/(g·cm-3)
18
?
?
?
?
【实验评估】
按该实验方案测出的河水密度比实际值 (选填“偏大”或“偏小”)。?
2.[梧州中考改编]小明想测他最爱吃的李子的密度,于是进行了如下实验操作:
(1)调节天平平衡后,把一颗新鲜的李子放到天平的左盘上,当天平平衡时右盘添加的砝码数和游码位置如图甲所示,则李子的质量为 g;?
(2)小明不小心把量筒打碎了,老师建议他用一个质量为50 g的烧杯代替量筒继续做实验,他思考后,接受了老师的建议,进行了如下操作:
①往烧杯倒入适量的水,把李子放入烧杯中,发现李子沉入水中,如图乙所示,用油性笔在烧杯壁记下此时水面位置M;
②用天平测出杯、水和李子的总质量为112 g;
③将李子从水中取出,再往烧杯中缓慢加水,使水面上升至记号M,如图丙所示;
④用天平测出杯和水的总质量为110 g。
根据实验数据,计算出李子的体积为 cm3,密度为 g/cm3(ρ水=1.0×103kg/m3)。?
密度的相关计算
类型1 等体积问题
1.如图,一只烧杯盛满水时,称得其总质量为400 g;放入一金属球溢出一部分水后,称得其总质量为900 g;取出金属球后,称得烧杯和剩余水的质量为300 g(忽略金属球沾的水)。求此金属球的密度。
2.如图a所示的小烧杯质量为32 g。现将一个质量为48 g的物块轻轻放入装满水的溢水杯(图b)中,刚好有一半的体积露出水面,溢出的水全部流入小烧杯(图c),测出小烧杯和水的总质量为80 g。
(1)求这个物块的密度;
(2)用这种材料制成一个质量为10 kg的工艺品,则这个工艺品的体积为多少?
类型2 图表问题
3.为测量某种液体的密度,小明利用天平和量杯测量了液体和量杯的总质量m及液体的体积V,得到几组数据并绘制出了m?V图像,如图所示。该液体的密度为多少?量杯的质量为多少?
4.在测定液体的密度时,小林测出了液体的体积、容器和液体的总质量,记录结果如表。求:
实验序号
一
二
三
液体的体积/cm3
16.5
35.0
40.0
液体和容器的总质量/g
21.4
39.9
M
(1)该液体的密度;
(2)容器的质量;
(3)M的值。
类型3 凑整问题
5.如图所示,一个容积V0 =500 cm3、质量m0 = 0.5 kg的瓶子里装有水。乌鸦为了喝到瓶子里的水,就衔了很多的小石块放到瓶子里,让水面上升到瓶口。若瓶内有质量m1 =0.4 kg的水(水的密度ρ水=1.0×103 kg/m3 ,石块密度ρ石 =2.6×103 kg/m3 )。求:
(1)瓶中水的体积V1 ;
(2)乌鸦投入瓶子中的石块的体积V2 ;
(3)乌鸦投入石块后,瓶子、石块和水的总质量m。
6.小华在家中发现一金属块,学习密度知识后,他做了如下实验:先用电子秤测出一个空玻璃瓶的质量为200 g,再装满水,测得总质量为700 g。将水倒出,烘干玻璃瓶,将金属块缓慢放入玻璃瓶中,测得玻璃瓶和金属块总质量为2200 g,然后再向玻璃瓶中加水至满,测出三者总质量为2500 g。求:
(1)玻璃瓶的容积;
(2)金属块的质量;
(3)金属块的密度。
类型4 空心问题
7.为判断一个铝球是否是实心的,小张对铝球进行了测量,实验数据如下(ρ铝=2.7×103 kg/m3,ρ水=1.0×103 kg/m3):
铝球的质量m/g
水的体积V1/mL
水和铝球的
总体积V2/mL
27
50.0
65.0
(1)该铝球是空心还是实心的?(根据计算结果说明)
(2)若铝球是空心的,空心部分的体积是多大?
(3)若在空心部分注满水,水的质量是多少?
类型5 混合密度问题
8.王慧同学利用所学知识,测量一件用合金制成的实心构件中铝所占的比例。她首先用天平测出构件的质量为374 g,用量杯测出构件的体积是100 cm3。已知合金由铝与钢两种材料合成,且铝的密度为2.7×103 kg/m3,钢的密度为7.9×103 kg/m3。如果构件的体积等于原来两种金属体积之和。求:
(1)这种合金的平均密度;
(2)这种合金中铝的质量占总质量的百分比。
测量物体的密度
【实验报告】
一、测量固体的密度
1.实验原理:ρ=mV。
2.实验器材:天平、量筒、细线、烧杯。
3.实验步骤
(1)用天平测出物体的质量m;
(2)向量筒里倒适量的水,测出水的体积V1;
(3)用细线系住物体放入量筒,测出两者的体积之和V2。
4.密度计算式:ρ=?mV2?V1 。?
5.误差分析
(1)若先测质量,后测量体积,仪器本身及读数会引起测量误差(既有质量误差,也有体积误差),但误差主要来源于体积的测量,误差偏大或偏小是不确定的;
(2)若先测体积,后测量质量,物体会沾有一部分水,使得测出的质量 偏大 ,进而测出的密度也 偏大 ,这种测量顺序是不可取的。?
二、测量液体的密度
1.实验原理:ρ=mV。
2.实验器材:天平、量筒、烧杯。
3.实验步骤
(1)用天平测出烧杯和液体的总质量m1;
(2)将烧杯中的液体部分倒入量筒中,用天平测出剩下的液体和烧杯的总质量m2;
(3)读出量筒中液体的体积V。
4.密度计算式:ρ=?m1?m2V 。?
5.其他方法误差分析
(1)先测液体体积V,后测液体质量m,因量筒中有残留液体(体积无法读出),所测的液体质量并不是体积V对应的质量,则测出的质量偏小,测得的密度 偏小 ;?
(2)先测液体质量m,后测液体体积V,由于烧杯中的液体倒入量筒会有一部分残留,则测出的体积偏小,测得的密度 偏大 。?
【针对训练】
1.某物理兴趣小组为检测学校附近某条河的水质,需要测量河水的密度。取样后,他们利用天平和量筒进行了测量,实验过程如下:
【实验步骤】
(1)用已调平衡的天平测出空烧杯的质量m1为18 g;
(2)向烧杯中倒入适量的河水,测出烧杯和河水的总质量m2,如图甲所示;
(3)将烧杯中的河水全部倒入量筒中,读出量筒中河水的体积V,如图乙所示。
【实验数据处理】
在下表中填入上述实验数据及计算结果。
烧杯的质
量m1/g
烧杯与河水
的质量m2/g
河水的质
量m/g
河水的体
积V/cm3
河水的密度
ρ/(g·cm-3)
18
49 ?
31 ?
30 ?
1.03 ?
【实验评估】
按该实验方案测出的河水密度比实际值 偏大 (选填“偏大”或“偏小”)。?
2.[梧州中考改编]小明想测他最爱吃的李子的密度,于是进行了如下实验操作:
(1)调节天平平衡后,把一颗新鲜的李子放到天平的左盘上,当天平平衡时右盘添加的砝码数和游码位置如图甲所示,则李子的质量为 12 g;?
(2)小明不小心把量筒打碎了,老师建议他用一个质量为50 g的烧杯代替量筒继续做实验,他思考后,接受了老师的建议,进行了如下操作:
①往烧杯倒入适量的水,把李子放入烧杯中,发现李子沉入水中,如图乙所示,用油性笔在烧杯壁记下此时水面位置M;
②用天平测出杯、水和李子的总质量为112 g;
③将李子从水中取出,再往烧杯中缓慢加水,使水面上升至记号M,如图丙所示;
④用天平测出杯和水的总质量为110 g。
根据实验数据,计算出李子的体积为 10 cm3,密度为 1.2 g/cm3(ρ水=1.0×103kg/m3)。?
密度的相关计算
类型1 等体积问题
1.如图,一只烧杯盛满水时,称得其总质量为400 g;放入一金属球溢出一部分水后,称得其总质量为900 g;取出金属球后,称得烧杯和剩余水的质量为300 g(忽略金属球沾的水)。求此金属球的密度。
解:溢出水的质量
m溢=m总-m剩=400 g-300 g=100 g
金属球的体积
V球=V溢=m溢ρ水=100 g1.0 g/cm3=100 cm3
金属球的质量
m=m1-m剩=900 g-300 g=600 g
金属球的密度
ρ=mV球=600 g100 cm3=6 g/cm3
2.如图a所示的小烧杯质量为32 g。现将一个质量为48 g的物块轻轻放入装满水的溢水杯(图b)中,刚好有一半的体积露出水面,溢出的水全部流入小烧杯(图c),测出小烧杯和水的总质量为80 g。
(1)求这个物块的密度;
(2)用这种材料制成一个质量为10 kg的工艺品,则这个工艺品的体积为多少?
解:(1)由题意知,物块浸入水中的体积等于它排开水的体积,即
V浸=V排=m水ρ水=m总?m1ρ水=80 g?32 g1.0 g/cm3=48 cm3
由题意知,物块的体积
V物=2V浸=2×48 cm3=96 cm3
则物块的密度为
ρ物=m物V物=48 g96 cm3=0.5 g/cm3=0.5×103 kg/m3
(2)这个工艺品的体积为
V'物=m' 物ρ物=10 kg0.5×103kg/m3=0.02 m3
类型2 图表问题
3.为测量某种液体的密度,小明利用天平和量杯测量了液体和量杯的总质量m及液体的体积V,得到几组数据并绘制出了m?V图像,如图所示。该液体的密度为多少?量杯的质量为多少?
解:设量杯的质量为m杯,液体的密度为ρ,由题图可知,当液体体积为V1=20 cm3时,液体和量杯的总质量m总1=m1+m杯=40 g
则ρ×20 cm3+m杯=40 g ①
当液体体积为V2=80 cm3时,液体和量杯的总质量m总2=m2+m杯=100 g
则ρ×80 cm3+m杯=100 g ②
联立①②,解得液体的密度ρ=1 g/cm3,m杯=20 g
4.在测定液体的密度时,小林测出了液体的体积、容器和液体的总质量,记录结果如表。求:
实验序号
一
二
三
液体的体积/cm3
16.5
35.0
40.0
液体和容器的总质量/g
21.4
39.9
M
(1)该液体的密度;
(2)容器的质量;
(3)M的值。
解:(1)第一次实验与第二次实验相比,液体体积的变化量
ΔV=35.0 cm3-16.5 cm3=18.5 cm3
液体和容器的总质量的变化量
Δm=39.9 g-21.4 g=18.5 g
该液体的密度
ρ=ΔmΔV=18.5 g18.5 cm3=1 g/cm3
(2)第一次实验时液体的质量
m1=ρV1=1 g/cm3×16.5 cm3=16.5 g
容器的质量
m容=m总1-m1=21.4 g-16.5 g=4.9 g
(3)第三次实验时液体的质量
m3=ρV3=1 g/cm3×40.0 cm3=40.0 g
液体和容器的总质量
m总3=m3+m容=40.0 g+4.9 g=44.9 g
即M=44.9
类型3 凑整问题
5.如图所示,一个容积V0 =500 cm3、质量m0 = 0.5 kg的瓶子里装有水。乌鸦为了喝到瓶子里的水,就衔了很多的小石块放到瓶子里,让水面上升到瓶口。若瓶内有质量m1 =0.4 kg的水(水的密度ρ水=1.0×103 kg/m3 ,石块密度ρ石 =2.6×103 kg/m3 )。求:
(1)瓶中水的体积V1 ;
(2)乌鸦投入瓶子中的石块的体积V2 ;
(3)乌鸦投入石块后,瓶子、石块和水的总质量m。
解:(1)瓶中水的体积
V1=m1ρ水=0.4 kg1.0×103kg/m3=4×10-4 m3=400 cm3
(2)瓶子中的石块的体积
V2=V0-V1=500 cm3-400 cm3=100 cm3
(3)石块的质量
m石=ρ石V2=2.6 g/cm3×100 cm3=260 g=0.26 kg
乌鸦投入石块后,瓶子、石块和水的总质量
m=m1+m0+m石=0.4 kg+0.5 kg+0.26 kg=1.16 kg
6.小华在家中发现一金属块,学习密度知识后,他做了如下实验:先用电子秤测出一个空玻璃瓶的质量为200 g,再装满水,测得总质量为700 g。将水倒出,烘干玻璃瓶,将金属块缓慢放入玻璃瓶中,测得玻璃瓶和金属块总质量为2200 g,然后再向玻璃瓶中加水至满,测出三者总质量为2500 g。求:
(1)玻璃瓶的容积;
(2)金属块的质量;
(3)金属块的密度。
解:(1)一满瓶水的质量为m水=m1-m0=700 g-200 g=500 g
由公式ρ=mV得,玻璃瓶的容积V瓶=V水=m水ρ水=500 g1 g/cm3=500 cm3
(2)金属块的质量为m金=m2-m0=2200 g-200 g=2000 g
(3)第2次向玻璃瓶中加入水的质量为Δm=2500 g-2200 g=300 g
这些水的体积为ΔV=Δmρ水=300 g1 g/ cm3=300 cm3
金属块的体积为V金=V瓶-ΔV=500 cm3-300 cm3=200 cm3
金属块的密度为ρ金=m金V金=2000 g200 cm3=10 g/cm3=1.0×104 kg/m3
类型4 空心问题
7.为判断一个铝球是否是实心的,小张对铝球进行了测量,实验数据如下(ρ铝=2.7×103 kg/m3,ρ水=1.0×103 kg/m3):
铝球的质量m/g
水的体积V1/mL
水和铝球的
总体积V2/mL
27
50.0
65.0
(1)该铝球是空心还是实心的?(根据计算结果说明)
(2)若铝球是空心的,空心部分的体积是多大?
(3)若在空心部分注满水,水的质量是多少?
解:(1)由ρ=mV可得,铝球中铝的体积
V铝=mρ铝=27 g2.7 g/cm3=10 cm3
因为V球=V2-V1=65.0 mL-50.0 mL=15.0 mL=15.0 cm3>10 cm3
所以该球是空心的。
(2)空心部分的体积
V空=V球-V铝=15 cm3-10 cm3=5 cm3
(3)在空心部分注满水后水的体积
V水=V空=5 cm3
由ρ=mV可得,水的质量
m水=ρ水V水=1.0 g/cm3×5 cm3=5 g
类型5 混合密度问题
8.王慧同学利用所学知识,测量一件用合金制成的实心构件中铝所占的比例。她首先用天平测出构件的质量为374 g,用量杯测出构件的体积是100 cm3。已知合金由铝与钢两种材料合成,且铝的密度为2.7×103 kg/m3,钢的密度为7.9×103 kg/m3。如果构件的体积等于原来两种金属体积之和。求:
(1)这种合金的平均密度;
(2)这种合金中铝的质量占总质量的百分比。
解:(1)这种合金的平均密度
ρ=mV=374 g100 cm3=3.74 g/cm3=3.74×103 kg/m3
(2)设铝的质量为m铝,钢的质量为m钢,则
m铝+m钢=374 g ①
由ρ=mV可得V=mρ,且构件的体积等于原来两种金属体积之和,则m铝ρ铝+m钢ρ钢=100 cm3
即m铝2.7 g/cm3+m钢7.9 g/cm3=100 cm3 ②
联立①②,解得m铝=216 g
则这种合金中铝的质量占总质量的百分比为216 g374 g×100%≈57.8%
同课章节目录
- 第一章 打开物理世界的大门
- 第一节 走进神奇
- 第二节 探索之路
- 第三节 站在巨人的肩膀上
- 第二章 运动的世界
- 第一节 动与静
- 第二节 长度与时间的测量
- 第三节 快与慢
- 第四节 科学探究:速度的变化
- 第三章 声的世界
- 第一节 科学探究:声音的产生与传播
- 第二节 声音的特性
- 第三节 超声与次声
- 第四章 多彩的光
- 第一节 光的反射
- 第二节 平面镜成像
- 第三节 光的折射
- 第四节 光的色散
- 第五节 科学探究:凸透镜成像
- 第六节 神奇的眼睛
- 第五章 质量与密度
- 第一节 质量
- 第二节 学习使用天平和量筒
- 第三节 科学探究:物质的密度
- 第四节 密度知识的应用
- 第六章 熟悉而陌生的力
- 第一节 力
- 第二节 怎样描述力
- 第三节 弹力与弹簧测力计
- 第四节 来自地球的力
- 第五节 科学探究:摩擦力
- 第七章 力与运动
- 第一节 科学探究:牛顿第一定律
- 第二节 力的合成
- 第三节 力的平衡
- 第八章 压强
- 第一节 压力的作用效果
- 第二节 科学探究:液体的压强
- 第三节 空气的“力量”
- 第四节 流体压强与流速的关系
- 第九章 浮力
- 第一节 认识浮力
- 第二节 阿基米德原理
- 第三节 物体的浮与沉
- 第十章 机械与人
- 第一节 科学探究:杠杆的平衡条件
- 第二节 滑轮及其应用
- 第三节 做功了吗
- 第四节 做功的快慢
- 第五节 机械效率
- 第六节 合理利用机械能
- 第十一章 小粒子与大宇宙
- 第一节 走进微观
- 第二节 看不见的运动
- 第三节 探索宇宙
