吉林省长春市九台区2020-2021学年高二下学期期末考试数学(理)试题 Word版含答案
文档属性
| 名称 | 吉林省长春市九台区2020-2021学年高二下学期期末考试数学(理)试题 Word版含答案 |  | |
| 格式 | doc | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-30 20:07:50 | ||
图片预览




文档简介
长春市九台区2020-2021学年高二下学期期末考试
数学理科试题
第Ⅰ卷(共 60分)
一、选择题:本题共12小题,每小题5分.在每小题给出的四个选项中,只有一个选项
是符合题目要求的.
1. 已知集合,,则( )
A. B.
C. D.
2. 在复平面内,复数对应的点位于( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
3. 已知命题,,命题,,则下列为真命题的是( )
A. B. C. D.
4.研究表明,我国研制的新冠灭活疫苗,人体接种这种疫苗需要接种两次,间隔2~4周,接种完第一剂以后,7天开始普遍产生抗体,接种完第二剂28天以后,中和抗体阳转率或者叫阳性率均达百分之百.也就是说,按照规范的免疫程序接种两剂我国研制的新冠灭活疫苗28天后,所有人都能产生足以抵抗新冠病毒的抗体,某研究所在500名志愿者身上进行了人体新冠灭活疫苗注射,接种完第一剂7天后发现这些志愿者均已经产生了稳定的免疫应答,这些志愿者的免疫反应蛋白的数值(单位:)近似服从正态分布,且在区间内的人数占总人数的98%,则这500名志愿者中免疫反应蛋白的数值 不大于的人数大约为( )
A.5 B.10 C.50 D.100
5.有红色、黄色小球各两个,蓝色小球一个,所有小球彼此不同,现将五球排成一行,颜色相同者不相邻,不同的排法共有( )种
A.48 B.72 C.78 D.84
6.甲乙二人争夺一场围棋比赛的冠军,若比赛为“五局三胜”制,甲在每局比赛中获胜的概率均为,且各局比赛结果相互独立,则在甲获胜得冠军的情况下,比赛进行了四局的概率为( ).
A. B. C. D.
7.已知变量关于变量的回归方程为,其一组数据如下表所示:
1 2 3 4 5
若,则的值大约为( )
A.4.94 B.5.74 C.6.81 D.8.04
8.已知平面向量,的夹角为,且对任意实数,恒成立,则( )
A. B. C. D.
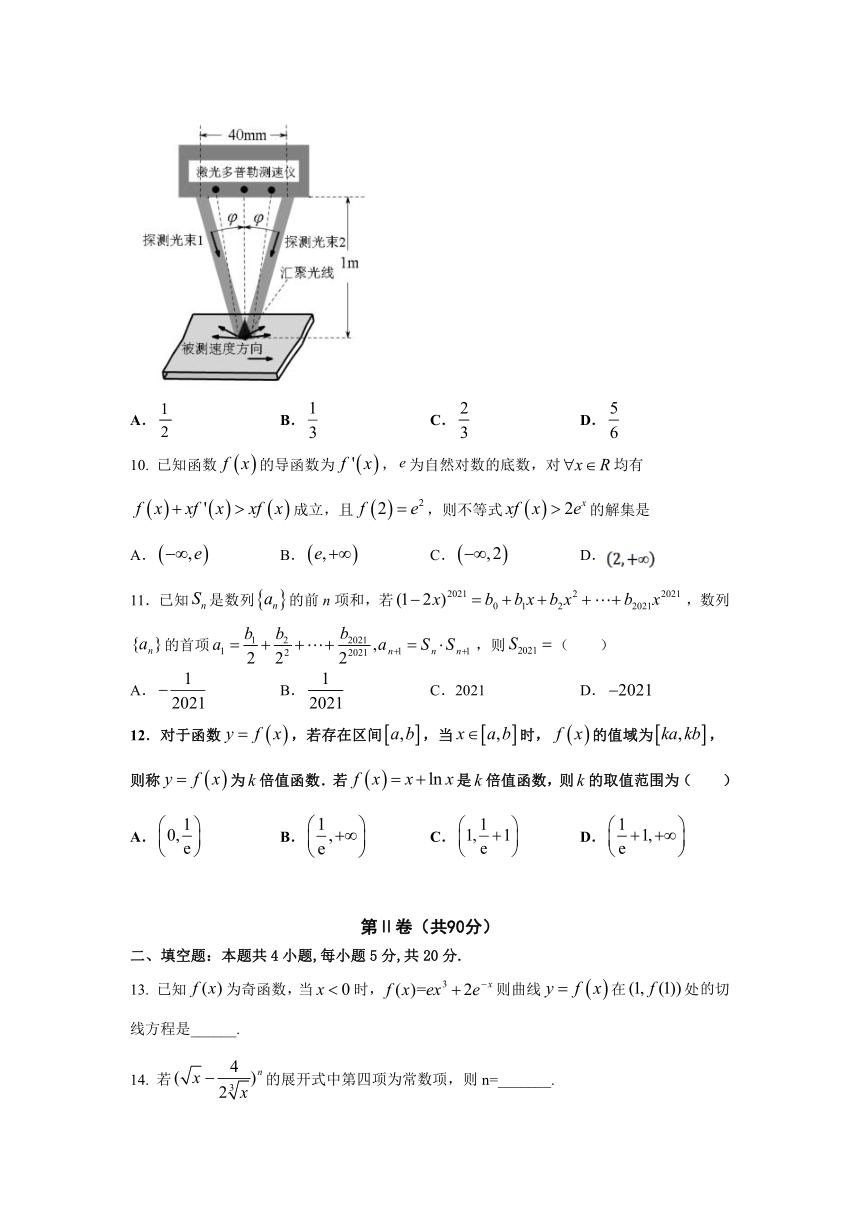
9.某校高一年级研究性学习小组利用激光多普勒测速仪实地测量复兴号高铁在某时刻的速度,其工作原理是:激光器发出的光平均分成两束射出,在被测物体表面汇聚,探测器接收反射光,当被测物体横向速度为零时,反射光与探测光频率相同,当横向速度不为零时,反射光相对探测光会发生频移,其中为测速仪测得被测物体的横向速度,为激光波长,为两束探测光线夹角的一半,如图,若激光测速仪安装在距离高铁处,可近似计算≈0.02,发出的激光波长为(),某次检验中可测频移范围为()至(),该高铁以运行速度(至)经过时,可测量的概率为( )
A. B. C. D.
10. 已知函数的导函数为,为自然对数的底数,对均有成立,且,则不等式的解集是
A. B. C. D.
11.已知是数列的前n项和,若,数列的首项,则( )
A. B. C.2021 D.
12.对于函数,若存在区间,当时,的值域为,则称为倍值函数.若是倍值函数,则的取值范围为( )
A. B. C. D.
第Ⅱ卷(共90分)
二、填空题:本题共4小题,每小题5分,共20分.
13. 已知为奇函数,当时,则曲线在处切线方程是______.
14. 若的展开式中第四项为常数项,则n=_______.
15. 我校5位同学报考了北京大学“强基计划”第I专业组,并顺利通过各项考核,已知5位同学将根据综合成绩和志愿顺序随机地进入教学类?物理学类?力学类这三个专业中的某一个专业,则这三个专业都有我校学生的概率是__________(结果用最简分数表示).
16.已知F1,F2分别为双曲线x2﹣=1的左、右焦点,过F2且倾斜角为θ的直线与双曲线的右支交于A,B两点,记△AF1F2的内切圆O1的半径为r1,△BF1F2的内切圆O2的半径为r2,圆O1的面积为S1,圆O2的面积为S2,则______________
①.θ的取值范围是(,) ②.直线O1O2与x轴垂直
③.若r1+r2=2,则|AB|=6 ④.S1+S2的取值范围是[2π,)
三、解答题:本题共5小题,每题12分,共70分.
17. 设三角形的内角??所对的边长分别是??,且.
(1)求的大小;
(2)若不是钝角三角形,求的取值范围.
18.如图,在直三棱柱中,正方形边长为3,,,M是线段上一点,设.
(1)若,证明:BD∥平面;
(2)若二面角的余弦值为,求的值.
19.国务院办公厅印发了《关于防止耕地“非粮化”稳定粮食生产的意见》,意见指出要切实稳定粮食生产,牢牢守住国家粮食安全的生命线.为了切实落实好稻谷?小麦?玉米三大谷物种植情况,某乡镇抽样调查了村庄部分耕地(包含永久农田和一般耕地)的使用情况,其中永久农田100亩,三大谷物的种植面积为90亩,棉?油?蔬菜等的种植面积为10亩;一般耕地50亩,三大谷物的种植面积为30亩,棉?油?蔬菜等的种植面积为20亩.
(1)以频率代替概率,求村庄每亩耕地(包括永久农田和一般耕地)种植三大谷物的概率;
(2)上级有关部门要恪促落实整个乡镇三大谷物的种植情况,现从本乡镇抽测5个村庄,每个村庄的三大谷物的种植情况符合要求的概率均为村庄每亩耕地(永久农田和一般耕地)种植三大谷物的概率.若抽测的村庄三大谷物的种植情况符合要求,则为本乡镇记1分,若不符合要求,记-1分.表示本乡镇的总积分,求的分布列及数学期望;
(3)目前在农村的劳动力大部分是中老年人,调查中发现,80位中老年劳动力中有65人种植三大谷物,其余种植棉?油?蔬菜等农作物;20位青壮年劳动力中有15人种植需要技术和体力,短期收益大的棉?油?蔬菜等农作物,其余种植三大谷物.请完成下表,并判断是否有的把握认为种植作物的种类与劳动力的年龄层次有关?
劳动力年龄层次 种植情况 合计
种植三大谷物 种植棉,油,蔬菜等
中老年劳动力
青壮年劳动力
合计
附:,其中.
0.10 0.05 0.025 0.010 0.001
2.706 3.841 5.024 6.635 10.828
20. 已知抛物线:的焦点为,为坐标原点.过点的直线与抛物线交于,两点.
(1)若直线与圆:相切,求直线的方程;
(2)若直线与轴的交点为.且,,试探究:是否为定值?若为定值,求出该定值;若不为定值,试说明理由.
21.已知函数.
(1)当时,求函数的单调区间;
(2)若恒成立,求实数的取值范围.
22.在直角坐标系xOy中,曲线C1的参数方程为(t为参数),以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρsin2θ=4cosθ.
(1)求曲线C1和C2的直角坐标方程;
(2)已知点P(1,),曲线C1与C2相交于A,B两点,求||.
23.已知函数,.
(1)求函数的图象与直线围成区域的面积;
(2)若对于,,且时,不等式恒成立,求实数的取值范围.
长春市九台区2020-2021学年高二下学期期末考试
数学理科试题答案
一、选择题:本题共12小题,每小题5分.在每小题给出的四个选项中,只有一个选项
是符合题目要求的.
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 C D C A A B C B A D A C
二、填空题:本题共4小题,每小题5分,共20分.
13. 14. 【答案】5 15. 16.②③④
三、解答题:本题共5小题,每题12分,共70分.
17.
【答案】(1);(2).
【详解】(1)因为
所以
由正弦定理,得
所以
又因为,所以;
(2)因为,
由,得:
由正弦定理得
当时,
当时,
所以.
18.【答案】(1)证明见解析;(2).
【详解】(1)
连接交于点N,连接,
则M,N分别为和的中点,∴;
∵平面,平面;
∴平面;
(2)以C为原点,,,分别为x轴,y轴,z轴正方向建立空间直角坐标系,
,,,设,其中;
则,,,
平面的法向量,平面的法向量;
∴,.
19.
【答案】(1);(2)分布列答案见解析,数学期望:;(3)表格答案见解析,有的把握认为种植作物的种类与劳动力的年龄层次有关.
【详解】
解:(1)设事件为“耕地(包括永久农田和一般耕地)种植三大谷物”,
则.
所以村庄每亩耕地种植三大谷物的概率为
(2)由(1)知,每个村庄的三大谷物的种植情况符合要求的概率均为
由题意知的所有可能取值为
则,
则该乡镇的总积分的分布列为
-5 -3 -1 1 3 5
(3)
劳动力年龄层次 种植情况 合
计
种植三大谷物 种植棉?油?蔬菜等
中老年劳动力 65 15 80
青壮年劳动力 5 15 20
合计 70 30 100
的观测值
因为
所以有的把握认为种植作物的种类与劳动力的年龄层次有关.
20. 【答案】(1);(2),理由见解析;
【分析】
【详解】(1)由题意知:且圆 半径为,圆心,即有在圆外,
∴设直线为,则圆心到直线的距离,
解之得:,即直线的方程为.
(2)由过的直线与抛物线交于,两点,与轴的交点为,即斜率存在且,设直线为,有,
联立直线方程与椭圆方程,有,可得,
设,,即有,
,,,,
由,,可得,,
∴,即可得为定值
21.【答案】(1)增区间为,减区间为;(2).
【详解】
(1)由题意,函数的定义域为,
且,
因为,可得,
令,即,解得;
令,即,解得,
所以的增区间为,减区间为.
(2)由恒成立,即恒成立,
设,
只需函数,
由,
①当时,由于,故,此时在上递减,
因此不存在,故不成立;
②当时,,因为,
令,即,解得;
令,即,解得,
所以的减区间为,増区间为,
所以,
由,即,可得,
令,可得,
设,可得,所以在上为单调递增函数,
又由,所以,即,解得,
综上所述,当时,恒成立,
所以实数的取值范围是.
22.解:(1)曲线C1的参数方程为(t为参数),消去参数t得:.
曲线C2的极坐标方程为ρsin2θ=4cosθ,根据转换为直角坐标方程为y2=4x.
(2)曲线C1的参数方程为(t为参数),转换为标准式为(t为参数),
代入y2=4x,
得到:,
所以,.
故.
23.【答案】(1);(2).
【解析】(1)由与围成的区域是,如图所示,
其中,,,
所以,到直线的距离为3,
故所求面积为.
(2)因为,,且,
所以,即,
若不等式恒成立,则有,
即,解不等式,
可得或或,
解之得或,
所以实数的取值范围为.
数学理科试题
第Ⅰ卷(共 60分)
一、选择题:本题共12小题,每小题5分.在每小题给出的四个选项中,只有一个选项
是符合题目要求的.
1. 已知集合,,则( )
A. B.
C. D.
2. 在复平面内,复数对应的点位于( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
3. 已知命题,,命题,,则下列为真命题的是( )
A. B. C. D.
4.研究表明,我国研制的新冠灭活疫苗,人体接种这种疫苗需要接种两次,间隔2~4周,接种完第一剂以后,7天开始普遍产生抗体,接种完第二剂28天以后,中和抗体阳转率或者叫阳性率均达百分之百.也就是说,按照规范的免疫程序接种两剂我国研制的新冠灭活疫苗28天后,所有人都能产生足以抵抗新冠病毒的抗体,某研究所在500名志愿者身上进行了人体新冠灭活疫苗注射,接种完第一剂7天后发现这些志愿者均已经产生了稳定的免疫应答,这些志愿者的免疫反应蛋白的数值(单位:)近似服从正态分布,且在区间内的人数占总人数的98%,则这500名志愿者中免疫反应蛋白的数值 不大于的人数大约为( )
A.5 B.10 C.50 D.100
5.有红色、黄色小球各两个,蓝色小球一个,所有小球彼此不同,现将五球排成一行,颜色相同者不相邻,不同的排法共有( )种
A.48 B.72 C.78 D.84
6.甲乙二人争夺一场围棋比赛的冠军,若比赛为“五局三胜”制,甲在每局比赛中获胜的概率均为,且各局比赛结果相互独立,则在甲获胜得冠军的情况下,比赛进行了四局的概率为( ).
A. B. C. D.
7.已知变量关于变量的回归方程为,其一组数据如下表所示:
1 2 3 4 5
若,则的值大约为( )
A.4.94 B.5.74 C.6.81 D.8.04
8.已知平面向量,的夹角为,且对任意实数,恒成立,则( )
A. B. C. D.
9.某校高一年级研究性学习小组利用激光多普勒测速仪实地测量复兴号高铁在某时刻的速度,其工作原理是:激光器发出的光平均分成两束射出,在被测物体表面汇聚,探测器接收反射光,当被测物体横向速度为零时,反射光与探测光频率相同,当横向速度不为零时,反射光相对探测光会发生频移,其中为测速仪测得被测物体的横向速度,为激光波长,为两束探测光线夹角的一半,如图,若激光测速仪安装在距离高铁处,可近似计算≈0.02,发出的激光波长为(),某次检验中可测频移范围为()至(),该高铁以运行速度(至)经过时,可测量的概率为( )
A. B. C. D.
10. 已知函数的导函数为,为自然对数的底数,对均有成立,且,则不等式的解集是
A. B. C. D.
11.已知是数列的前n项和,若,数列的首项,则( )
A. B. C.2021 D.
12.对于函数,若存在区间,当时,的值域为,则称为倍值函数.若是倍值函数,则的取值范围为( )
A. B. C. D.
第Ⅱ卷(共90分)
二、填空题:本题共4小题,每小题5分,共20分.
13. 已知为奇函数,当时,则曲线在处切线方程是______.
14. 若的展开式中第四项为常数项,则n=_______.
15. 我校5位同学报考了北京大学“强基计划”第I专业组,并顺利通过各项考核,已知5位同学将根据综合成绩和志愿顺序随机地进入教学类?物理学类?力学类这三个专业中的某一个专业,则这三个专业都有我校学生的概率是__________(结果用最简分数表示).
16.已知F1,F2分别为双曲线x2﹣=1的左、右焦点,过F2且倾斜角为θ的直线与双曲线的右支交于A,B两点,记△AF1F2的内切圆O1的半径为r1,△BF1F2的内切圆O2的半径为r2,圆O1的面积为S1,圆O2的面积为S2,则______________
①.θ的取值范围是(,) ②.直线O1O2与x轴垂直
③.若r1+r2=2,则|AB|=6 ④.S1+S2的取值范围是[2π,)
三、解答题:本题共5小题,每题12分,共70分.
17. 设三角形的内角??所对的边长分别是??,且.
(1)求的大小;
(2)若不是钝角三角形,求的取值范围.
18.如图,在直三棱柱中,正方形边长为3,,,M是线段上一点,设.
(1)若,证明:BD∥平面;
(2)若二面角的余弦值为,求的值.
19.国务院办公厅印发了《关于防止耕地“非粮化”稳定粮食生产的意见》,意见指出要切实稳定粮食生产,牢牢守住国家粮食安全的生命线.为了切实落实好稻谷?小麦?玉米三大谷物种植情况,某乡镇抽样调查了村庄部分耕地(包含永久农田和一般耕地)的使用情况,其中永久农田100亩,三大谷物的种植面积为90亩,棉?油?蔬菜等的种植面积为10亩;一般耕地50亩,三大谷物的种植面积为30亩,棉?油?蔬菜等的种植面积为20亩.
(1)以频率代替概率,求村庄每亩耕地(包括永久农田和一般耕地)种植三大谷物的概率;
(2)上级有关部门要恪促落实整个乡镇三大谷物的种植情况,现从本乡镇抽测5个村庄,每个村庄的三大谷物的种植情况符合要求的概率均为村庄每亩耕地(永久农田和一般耕地)种植三大谷物的概率.若抽测的村庄三大谷物的种植情况符合要求,则为本乡镇记1分,若不符合要求,记-1分.表示本乡镇的总积分,求的分布列及数学期望;
(3)目前在农村的劳动力大部分是中老年人,调查中发现,80位中老年劳动力中有65人种植三大谷物,其余种植棉?油?蔬菜等农作物;20位青壮年劳动力中有15人种植需要技术和体力,短期收益大的棉?油?蔬菜等农作物,其余种植三大谷物.请完成下表,并判断是否有的把握认为种植作物的种类与劳动力的年龄层次有关?
劳动力年龄层次 种植情况 合计
种植三大谷物 种植棉,油,蔬菜等
中老年劳动力
青壮年劳动力
合计
附:,其中.
0.10 0.05 0.025 0.010 0.001
2.706 3.841 5.024 6.635 10.828
20. 已知抛物线:的焦点为,为坐标原点.过点的直线与抛物线交于,两点.
(1)若直线与圆:相切,求直线的方程;
(2)若直线与轴的交点为.且,,试探究:是否为定值?若为定值,求出该定值;若不为定值,试说明理由.
21.已知函数.
(1)当时,求函数的单调区间;
(2)若恒成立,求实数的取值范围.
22.在直角坐标系xOy中,曲线C1的参数方程为(t为参数),以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρsin2θ=4cosθ.
(1)求曲线C1和C2的直角坐标方程;
(2)已知点P(1,),曲线C1与C2相交于A,B两点,求||.
23.已知函数,.
(1)求函数的图象与直线围成区域的面积;
(2)若对于,,且时,不等式恒成立,求实数的取值范围.
长春市九台区2020-2021学年高二下学期期末考试
数学理科试题答案
一、选择题:本题共12小题,每小题5分.在每小题给出的四个选项中,只有一个选项
是符合题目要求的.
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 C D C A A B C B A D A C
二、填空题:本题共4小题,每小题5分,共20分.
13. 14. 【答案】5 15. 16.②③④
三、解答题:本题共5小题,每题12分,共70分.
17.
【答案】(1);(2).
【详解】(1)因为
所以
由正弦定理,得
所以
又因为,所以;
(2)因为,
由,得:
由正弦定理得
当时,
当时,
所以.
18.【答案】(1)证明见解析;(2).
【详解】(1)
连接交于点N,连接,
则M,N分别为和的中点,∴;
∵平面,平面;
∴平面;
(2)以C为原点,,,分别为x轴,y轴,z轴正方向建立空间直角坐标系,
,,,设,其中;
则,,,
平面的法向量,平面的法向量;
∴,.
19.
【答案】(1);(2)分布列答案见解析,数学期望:;(3)表格答案见解析,有的把握认为种植作物的种类与劳动力的年龄层次有关.
【详解】
解:(1)设事件为“耕地(包括永久农田和一般耕地)种植三大谷物”,
则.
所以村庄每亩耕地种植三大谷物的概率为
(2)由(1)知,每个村庄的三大谷物的种植情况符合要求的概率均为
由题意知的所有可能取值为
则,
则该乡镇的总积分的分布列为
-5 -3 -1 1 3 5
(3)
劳动力年龄层次 种植情况 合
计
种植三大谷物 种植棉?油?蔬菜等
中老年劳动力 65 15 80
青壮年劳动力 5 15 20
合计 70 30 100
的观测值
因为
所以有的把握认为种植作物的种类与劳动力的年龄层次有关.
20. 【答案】(1);(2),理由见解析;
【分析】
【详解】(1)由题意知:且圆 半径为,圆心,即有在圆外,
∴设直线为,则圆心到直线的距离,
解之得:,即直线的方程为.
(2)由过的直线与抛物线交于,两点,与轴的交点为,即斜率存在且,设直线为,有,
联立直线方程与椭圆方程,有,可得,
设,,即有,
,,,,
由,,可得,,
∴,即可得为定值
21.【答案】(1)增区间为,减区间为;(2).
【详解】
(1)由题意,函数的定义域为,
且,
因为,可得,
令,即,解得;
令,即,解得,
所以的增区间为,减区间为.
(2)由恒成立,即恒成立,
设,
只需函数,
由,
①当时,由于,故,此时在上递减,
因此不存在,故不成立;
②当时,,因为,
令,即,解得;
令,即,解得,
所以的减区间为,増区间为,
所以,
由,即,可得,
令,可得,
设,可得,所以在上为单调递增函数,
又由,所以,即,解得,
综上所述,当时,恒成立,
所以实数的取值范围是.
22.解:(1)曲线C1的参数方程为(t为参数),消去参数t得:.
曲线C2的极坐标方程为ρsin2θ=4cosθ,根据转换为直角坐标方程为y2=4x.
(2)曲线C1的参数方程为(t为参数),转换为标准式为(t为参数),
代入y2=4x,
得到:,
所以,.
故.
23.【答案】(1);(2).
【解析】(1)由与围成的区域是,如图所示,
其中,,,
所以,到直线的距离为3,
故所求面积为.
(2)因为,,且,
所以,即,
若不等式恒成立,则有,
即,解不等式,
可得或或,
解之得或,
所以实数的取值范围为.
同课章节目录
