1.1 菱形的性质与判定(含解析)-2021年北师大版九年级数学上册培优训练
文档属性
| 名称 | 1.1 菱形的性质与判定(含解析)-2021年北师大版九年级数学上册培优训练 |  | |
| 格式 | docx | ||
| 文件大小 | 254.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-30 11:23:46 | ||
图片预览




文档简介
1.1 菱形的性质与判定-2021年北师大版九年级数学上册培优训练
一、选择题
1.折叠矩形纸片ABCD,使点B落在点D处,折痕为MN,已知AB=8,AD=4,则MN的长是(?? )
A.?535???????????????????????????????B.?2 5????????????????????????C.?735?????????????????????????D.?4 5
2.将一张三角形纸片按如图步骤①至④折叠两次得图⑤,然后剪出图⑤中的阴影部分,则阴影部分展开铺平后的图形是(?? )
A.?等腰三角形????????????????????B.?直角三角形???????????????C.?矩形??????????????????D.?菱形
3.如图,已知点P是菱形 ABCD 的对角线 AC 延长线上一点,过点P分别作 AD 、 DC 延长线的垂线,垂足分别为点E、F.若 ∠ABC=120° , AB=2 ,则 PE-PF 的值为(?? )
A.?32???????????????????????????????B.?3???????????????????????????????C.?2??????????????????????????????????D.?52
4.如图,AC是菱形ABCD的对角线,P是AC上一个动点,过点P分别作AB、BC的垂线,垂足分别是F和E . 若菱形ABCD的周长是12cm,面积是6cm2 , 则PE+PF的值是(??? )
A.?1.5??????????????????????????????????????B.?1?????????????????????C.?2????????????????????????????????D.?4
5.如图,四边形 ABCD 是菱形,对角线 AC , BD 相交于点 O , AC=63 , BD=6 ,点 P 是 AC 上一动点,点 E 是 AB 的中点,则 PD+PE 的最小值为(??? )
A.?33??????????????????????????????B.?63???????????????????????????C.?3???????????????????????????D.?62
6.如图,在 △ABC 中, AB=AC , △DBC 和 △ABC 关于直线BC对称,连接AD , 与BC相交于点O , 过点C作 CE⊥CD ,垂足为C , 与AD相交于点E . 若 AD=8 , BC=6 ,则 2OE+AEBD 的值为(?? )
A.?43????????????????????????????B.?34???????????????C.?53?????????????????????????????D.?54
7.如图,在菱形 ABCD 中,按如下步骤作图:①分别以点C和点D为圆心,大于 12CD 长为半径作弧,两弧交于点 M、N ;②作直线 MN ,且 MN 恰好经过点A,与 CD 交于点E,连接 BE ,若 AD=6 ,则 BE 的长为(??? )
A.?37??????????????????????B.?33????????????????????????C.?4??????????????????????D.?25
8.如图,在菱形ABCD中,M,N分别在AB,CD上,且AM=CN,MN与AC交于点O,连接BO.若∠DAC=26°,则∠OBC的度数为(?? )
A.?54°???????????????????B.?64°???????????????????????????C.?74°????????????????????????D.?26°
9.如图,在菱形 ABCD 中,点 P 是对角线 BD 上一点, Q 是 BC 中点,若菱形周长是16, ∠A=120° ,则 PC+PQ 的最小值为(??? )
A.?2 3?????????????????????????B.?2??????????????????????????C.?3????????????????????????D.?33
10.如图1,点F从边长为5的菱形ABCD的顶点A出发,沿折线A-D-B以1cm/s的速度匀速运动到点B,点F运动时,△FBC的面积 y(cm2) 与时间 x(s) 之间的函数关系如图2所示,则 a 的值为(?? )
A.?8?????????????????????????B.?9?????????????????????????????C.?5+10?????????????????D.?5+23
二、填空题
11.如图,在菱形ABCD中,E,F分别在BC,DC上,BE=DF,AE=AB,若∠EAF=30°,则∠D的度数是________。
12.如图,在平行四边形ABCD中, AE平分∠BAD交BC于点E , 过点E作AE的垂线交CD于点F , 若CF=1,AD=5,则AB=________.
13.如图,四边形 ABCD 为菱形, ∠ABC=70° ,延长 BC 到 E ,在 ∠DCE 内作射线 CM ,使得 ∠ECM=15° ,过点 D 作 DF⊥CM ,垂足为 F ,若 DF=5 ,则对角线 BD 的长为________.(结果保留根号)
14.如图,在菱形 ABCD 中, ∠BAD=60° ,点E在边 BC 上,将 △ABE 沿直线 AE 翻折180°,得到 △AB'E ,点B的对应点是点 B' 若 AB'⊥BD , BE=2 ,则 BB' 的长是________.
15.已知菱形 ABCD 的面积为 23 ﹐点E是一边 BC 上的中点,点P是对角线 BD 上的动点.连接 AE ,若AE平分 ∠BAC ,则线段 PE 与 PC 的和的最小值为________,最大值为________.
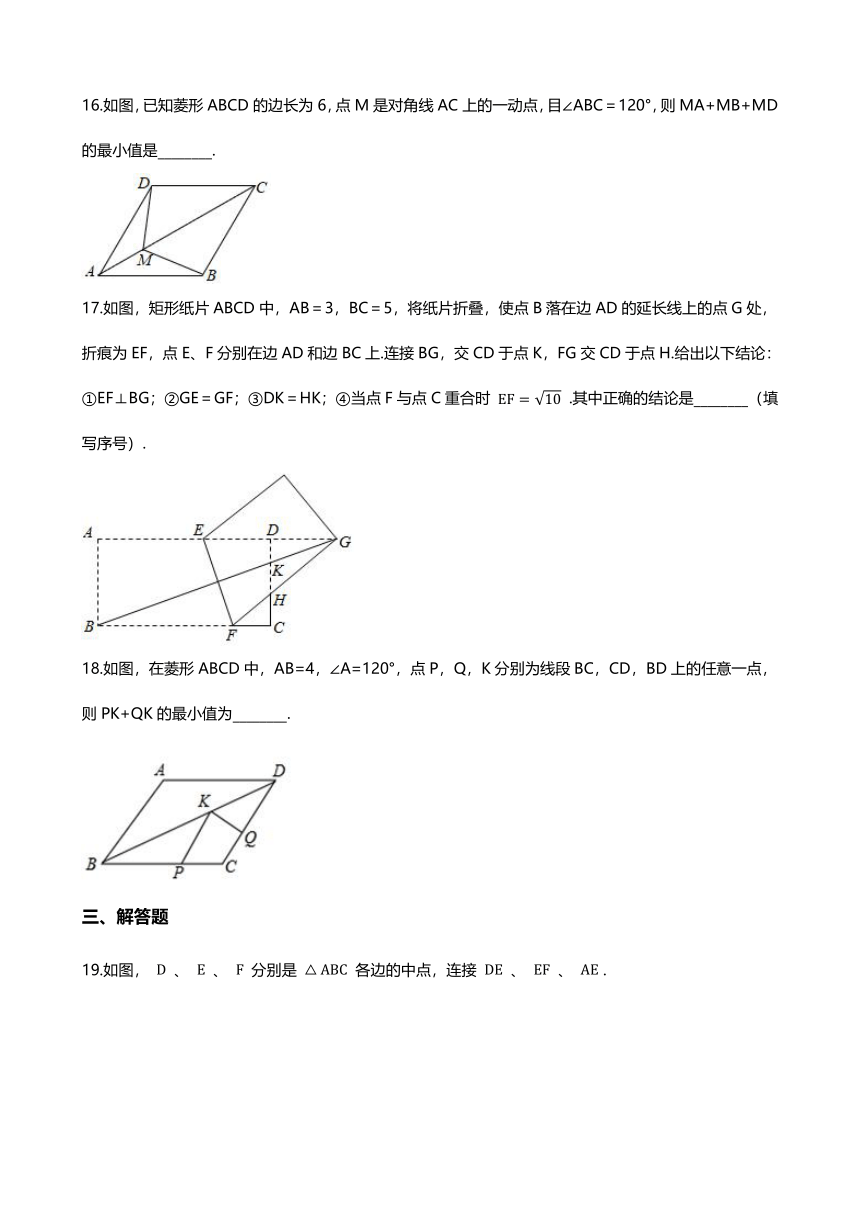
16.如图,已知菱形ABCD的边长为6,点M是对角线AC上的一动点,目∠ABC=120°,则MA+MB+MD的最小值是________.
17.如图,矩形纸片ABCD中,AB=3,BC=5,将纸片折叠,使点B落在边AD的延长线上的点G处,折痕为EF,点E、F分别在边AD和边BC上.连接BG,交CD于点K,FG交CD于点H.给出以下结论:①EF⊥BG;②GE=GF;③DK=HK;④当点F与点C重合时 EF=10 .其中正确的结论是________(填写序号).
18.如图,在菱形ABCD中,AB=4,∠A=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为________.
三、解答题
19.如图, D 、 E 、 F 分别是 △ABC 各边的中点,连接 DE 、 EF 、 AE .
(1)求证:四边形 ADEF 为平行四边形;
(2)加上条件? ▲ ?后,能使得四边形 ADEF 为菱形,请从① ∠BAC=90° ;② AE 平分 ∠BAC ;③ AB=AC ,这三个条件中选择条件填空(写序号),并加以证明.
20.在菱形ABCD中,∠ADC=60°,点F为CD上任意一点(不与C、D重合),过点F作CD的垂线,交BD于点E,连结AE。
(1)①依题意补全图1;
②写出线段EF、CF、AE之间得等量关系,并说明理由;
(2)在图1中,将△DEF绕点D逆时针旋转,当F、E、C在一条直线上,如图2所示,请判断EF、CE、AE之间的等量关系,写出判断思路(可以不写出证明过程).
21.如图,在四边形 ABCD 中,对角线 AC 与 BD 交于点O,已知 OA=OC , OB=OD ,过点O作 EF⊥BD ,分别交 AB 、 DC 于点E,F,连接 DE , BF .
(1)求证:四边形 DEBF 是菱形:
(2)设 AD//EF , AD+AB=12 , BD=43 ,求 AF 的长.
22.如图,四边形 PNQM 为菱形,延长 MP 使得 PB=MP ,延长 NQ 使得 QD=NQ ,延长 BN 使得 NC=BN ,延长 DM 使得 DM=MA ,连接 AB , CD .
(1)求证:四边形 BNDM 是平行四边形.
(2)猜想:四边形 ABCD 是哪种特殊的四边形?并证明你的猜想.
23.四边形 ABCD 为菱形, BD 为对角线,在对角线 BD 上任取一点 E ,连接 CE ,把线段 CE 绕点 C 顺时针旋转得到线段 CF ,使得 ∠ECF=∠BCD ,点 E 的对应点为点 F ,连接 DF .
?
(1)如图1,求证: BE=DF ;
(2)如图2,若 ∠DFC=2∠DBC ,在不添加任何辅助线的前提下,请直接写出五对线段,使每对线段的和等于 BD ( BE 和 DE 除外).
24.已知:平行四边形 ABCD ,对角线 AC , BD 相交于点 O . E 是 AD 的中点,连接 OE 并延长至 F 使得 OE=EF ,连接 FD , FC , FC 交 BD 于点 G .
求证:
(1)△FGD≌△CGO .
(2)当 AB 与 AC 有怎样的数量关系时,四边形 FOCD 是菱形,并说明理由.
25.在Rt△ABC中,∠B=90°,AC =20,∠A=60°,点D从点C出发沿CA方向以每秒2个单位长的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动,设点D、E运动的时间是t秒(t>0),过点D作DF⊥BC于点F , 连接DE、EF .
(1)求证:四边形AEFD是平行四边形;
(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,说明理由;
(3)当t为何值时,△DEF为直角三角形?请说明理由.
答案
一、选择题
1.解:如图,连接BM,
由折叠可知,MN垂直平分BD,
∴OD=OB, ?
又AB∥CD,
∴∠MDO=∠NBO,∠DMO=∠BNO, ?
∴ △ BON≌ △ DOM,
∴ON=OM,
∴四边形BMDN为菱形(对角线互相垂直平分的四边形是菱形),
∴DN=BN=BM=DM, ?
设DN=NB=x,则AN=8﹣x,
在Rt △ ABD中,由勾股定理得:BD= AD2+AB2 = 45 ,
在Rt △ ADN中,由勾股定理得:AD2+AN2=DN2 ,
即42+(8﹣x)2=x2 ,
解得x=5,
根据菱形计算面积的公式,得
BN×AD= 12 ×MN×BD,
即5×4= 12 ×MN× 45 ,
解得MN= 25 .
故答案为:B.
2.如图,由题意可知,剪下的图形是四边形BACD,
由折叠的性质可知CA = AB,
∴△ABC是等腰三角形,
又∵△ABC和△BCD关于直线CD对称,
∴AB=BD=AC=CD,
∴四边形BACD是菱形,
故答案为:D.
3.解:∵四边形ABCD是菱形且∠ABC=120°,AB=2,
∴AB=BC=CD=DA=2,∠BAD=60°,AC⊥BD,
∴∠CAE=30?,
∵AC⊥BD,∠CAE=30°,AD=2,
∴AC= 222-12=23 ,
∴AP= 23 +PC,
在直角△AEP中,
∵∠PAE=30°,AP= 23 +PC,
∴PE= 12 AP= 3 + 12 PC,
在直角△PFC中,
∵∠PCF=30°,
∴PF= 12 PC,
∴ PE-PF = 3 + 12 PC- 12 PC= 3 ,
故答案为:B.
4.如图,连接PB
∵四边形ABCD是菱形,其周长为12cm
∴AB=BC=3cm, S△ABC=12S菱形=3 cm2
∵ S△PAB+S△PBC=S△ABC ,PF⊥AB , PE⊥BC
∴ 12AB·PF+12BC·PE=3
即PE+PF=2cm
故答案为:C.
5.解:如图,连接 DE ,
由两点之间线段最短得:当点 D,P,E 共线时, PD+PE 取最小值,最小值为 DE ,
∵ 四边形 ABCD 是菱形, AC=63 , BD=6 ,
∴AB=AD,OB=12BD=3,OA=12AC=33,AC⊥BD ,
∴AB=OA2+OB2=6 ,
∴AB=AD=BD=6 ,
∴△ABD 是等边三角形,
∵ 点 E 是 AB 的中点,
∴AE=12AB=3,DE⊥AB ,
∴DE=AD2-AE2=62-32=33 ,
即 PD+PE 的最小值为 33 ,
故答案为:A.
6.解:∵ AB=AC , △DBC 和 △ABC 关于直线BC对称,
∴AB=AC=CD=BD ,
∴四边形ABDC是菱形,
∴BC⊥AD,OC=OB,OA=OD,
∵ AD=8 , BC=6 ,
∴OC=OB=3,OA=OD=4,
在Rt△COD中,OC=3,OD=4,
∴DC= 32+42=5 ,
∴AB=AC=CD=BD =5,
∵ CE⊥CD ,
∴ CE2+CD2=DE2 , CE2=OE2+CO2 ,
∴ OE2+32+52=(OE+4)2 ,
∴ OE=94 ,
∴ 2OE+AEBD=OE+AE+OEBD=4+945=54 ,
故答案为:D .
7.解:根据作图,知AE是线段CD的垂直平分线,
∵四边形ABCD是菱形,
∴DE= 12 AD,∴∠DAE=30°,∠D=60°,∠BAE=90°,
在直角三角形ADE中,根据勾股定理,得AE= 62-32 = 33 ,
在直角三角形BAE中,根据勾股定理,得BE= 62+(33)2 = 37 .
故答案为:A.
8.∵四边形ABCD为菱形,
∴AB∥CD,AB=BC,
∴∠MAO=∠NCO,∠AMO=∠CNO,
在△AMO和△CNO中,
{∠MAO=∠NCOAM=CN∠AMO=∠CNO ,
∴△AMO≌△CNO(ASA),
∴AO=CO,
∵AB=BC,
∴BO⊥AC,
∴∠BOC=90°,
∵∠DAC=26°,
∴∠BCA=∠DAC=26°,
∴∠OBC=90°﹣26°=64°.
故答案为:B.
9.解:如图,由菱形的对称轴可知,点 A 和点 C 关于 BD 对称,连接 AQ , AQ 即为所求 PC+PQ 的最小值.
连接 AC ,
∵∠BAD=120° ,四边形 ABCD 是菱形,
∴∠ABC=60° , AB=BC ,
∴△ABC 是等边三角形,
∵ 点 Q 为 BC 的中点,
∴AQ⊥BC ,
∵ 菱形 ABCD 的周长为16,
∴AB=BC=4 ,
在 Rt△ABQ 中, ∠ABC=60° ,
∴∠BAQ=30° ,
∴BQ=12AB=12×4=2 ,
∴AQ=AB2-BQ2=42-22=23 .
故答案为:A.
10.解:过点D作DH⊥BC,如图:
∵菱形的边长为5,
∴ BC=5
当x=5时,y=7.5, y=12BC·DH
∴DH=3,
∴ CH=52-32=4 ,
∴ BH=5-4=1
Rt△BDH中,可得 BD=12+32=10 ,
∴AD+DB= 5+10
故答案为:C.
二、填空题
11.解:∵四边形ABCD是菱形,
∴AB=AD,∠B=∠D,
∵BE=FD,
∴△ABE≌△ADF(SAS),
∴AE=AF,∠BAE=∠DAF,
设∠B=x,∠BAE=y,
∵∠BAE+∠B+∠AEB=2x+y=180°,∠BAD+∠B=2y+x+30°=180°,
∴4x+2y-2y-x-30°=180°,
整理得3x=210°,
∴x=70°,
故答案为:70°.
12.过点E作EG//AB交AD于G,易得四边形ABCG是平行四边形,
又 AE平分∠BAD ,可得∠BAE=∠GAE=∠AEB,
∴AB=AE,四边形ABCG是菱形。
∴∠GBE=12∠ABE,AE⊥BG,
又AE⊥EF,故BG//EF。
∴∠GBE=∠FEC,
∵EG//AB,
∴∠BAE=∠GEC。
∴∠FEC=12∠GEC
故易得∠FEC=EFC。
∴EC=EF=1。
易得四边形ECDG是平行四边形。
可设AB=AG=x,
故GD=5-x,又EC=GD。
∴5-x=1,得x=4?
∴AB=4
13.解:连接AC,如图,
∵四边形ABCD是菱形,
∴AB//CD, ∠DOC=90° ,BD=2DO
∴ ∠DCE=∠ABC=70°
∵ ∠ECM=15°
∴ ∠DCM=55°
∵ DF⊥CM
∴ ∠CDF=35°
∵四边形ABCD是菱形,
∴ ∠CDB=12∠ADC=12∠ABC=35°
∴ ∠CDF=∠CDO
在 ΔCDO 和 ΔCDF 中,
{∠CDO=∠CDF∠COD=∠CFD=90°CD=CD ?
∴ ΔCDO ≌ ΔCDF
∴ DO=DF=5
∴ BD=2DO=25
故答案为: 25 .
14.解:∵四边形 ABCD 是菱形,
∴ AB=AD,AD//BC ,
∵ ∠BAD=60° ,
∴ ∠ABE=120° , △ABD 是等边三角形,即 ∠ABD=60° ,
∵ AB'⊥BD ,
∴ ∠BAB'=30° ,
由折叠的性质可得 ∠BAE=∠EAB'=15° , BE=B'E=2 , ∠BEA=∠B'EA ,
在 △BEA 中,由三角形内角和可得 ∠BEA=45° ,
∴ ∠BEA=∠B'EA=45° ,即 ∠BEB'=90° ,
∴ △BEB' 是等腰直角三角形,
∴ BB'=2BE=22 ;
故答案为 22 .
15.解:如图,连接 PC ,
∵ ? E 是 BC 的中点,AE平分 ∠BAC ,
∴AB=AC ,
∴ △ABC 是等腰三角形,
又 ∵ 四边形 ABCD 是菱形,则 AB=BC ,
∴ ? △ABC 是等边三角形,
∵ ?已知菱形 ABCD 的面积为 23 ,
设菱形的边长为 a (a>0)
则 AE=a2-(a2)2=32a ,
∵ ? S=BC×AE ?,
∴ ? 23=a×32a ,
解得: a=2 ,
∴AE=3 ?,
∵A、C 关于 BD 对称,
PE + PC =PE+PA ≥ AE =3 ,
则 PE + PC 最小值为: 3 ;
当点P与点D重合时 PE + PC 最大,
过E作 EH⊥BD 垂足为H,
∵ ?四边形 ABCD 是菱形,
∴EH//OC ,
∵ E 是 BC 的中点,
∴EH=12OC=14AC=12 ?,
OH=12OB=32 ?,
∴DH=DO+OH=323 ?,
在 Rt△DHE 中,DE=DH2+HE2
(323)2+(12)2=7 ,
则 DE+DC=2+7 ,
∴ PE + PC 最大为: 2+7 .
16.如图,作DE⊥AB于E点,连接BD,
∵菱形ABCD中,∠ABC=120°,
∴∠DAB=60°,则△ABD为等边三角形,
∴∠MAE=30°,
∴AM=2ME,
∵MD=MB,
∴MA+MB+MD=2ME+2MD=2DE,
根据垂线段最短,此时DE最短,即MA+MB+MD最小,
∵菱形的边长为6,
∴AB=6,AE=3,
∴ DE=AD2-AE2=33 ,
∴ 2DE=63 ,
∴MA+MB+MD最小值为 63 ,
故答案为: 63 .
17.解:连接BE,由折叠可知BO=GO,
∵EG//BF,
∴∠EGO=∠FBO,
在△EOG和△FOB中,
{∠EGO=∠FBO∠EOG=∠FOBBO=GO ,
∴△EOG≌△FOB(AAS) ,
∴EG=BF,
∴四边形EBFG是平行四边形,
由折叠可知BE=EG,
则四边形EBFG为菱形,
故EF⊥BG,GE=GF,
∴①②正确;
∵四边形EBFG为菱形,
过K作kM⊥FG于M,???????????????????????
∴KG平分∠DGH,KD⊥EG,
∴KD=KM,
在Rt△KMH中,KH为斜边,
∴KH > KM=KD,
∴③错误;
当点F与点C重合时,BE=BF=BC=5,AB=3,
在Rt△ABE中,由勾股定理AE= BE2-AB2=52-32=4 ,
∴ED=AD-AE=5-4=1,
在Rt△EDC中,由勾股定理EF= CD2+ED2=32+12=10 ,
∴④正确.
综合,正确的为①②④.
故答案为:①②④.
18.解:如图,作点P关于BD的对称点P′,作P′Q⊥CD交BD于K,交CD于Q,
则P′Q即为PK+QK的最小值,
作AE⊥CD交CD于E,易得AE=P′Q,
在菱形ABCD中,∵AB=4,∠A=120°,
所以AD=4,∠D=60°,
∴ AE=4×32=23
∴PK+QK的最小值为 23 .
三、解答题
19.(1)证明:已知 D 、 E 是 AB 、 BC 中点
∴ DE//AC
又∵ E 、 F 是 BC 、 AC 的中点
∴ EF//AB
∵ DE//AF
∴ EF//AD
∴四边形 ADEF 为平行四边形
(2)解:②或③;证明:选② AE 平分 ∠BAC
∵ AE 平分 ∠BAC
∴ ∠DAE=∠FAE
又∵平行四边形 ADEF
∴ EF//DA
∴ ∠FAE=∠AEF
∴ AF=EF
∴平行四边形 ADEF 是菱形
选③ AB=AC
∵ EF//AB 且 EF=12AB
DE//AC 且 DE=12AC
又∵ AB=AC
∴ EF=DE
∴平行四边形 ADEF 为菱形
故答案为:②或③
20. (1)解:①依题意补全图形如图所示:
②连接CE,
∵EF⊥CD
∴∠EFC=90°
∴CE=EF2+CF2
又∵四边形ABCD为菱形
∴BD⊥AC,BD平分AC
∴AE=CE
∴AE2=EF2+CF2
(2)EFCE、AE之间的等量关系是:AE-CE+2EF
判断:如图
延长EF至G,使EF=FG,连接DG
∴EG=2EF
∵DF⊥CF
∴DE=DG,∠EDG=2∠EDF
又∵四边形ABCD为菱形
∴AD=CD,∠ADC=2∠ODC=60°
又由旋转得∠ODC=∠EDF
∴∠ADC=∠EDG
∴∠ADE=2∠CDG
在△ADE和△CDG中 {AD=CD∠ADE=∠CDGDE=DG
∴△ADE≌△CDG
∴AE=CG=CE+EG=CE+2EF
∴AE=CE+2EF
21. (1)证明:∵ OA=OC , OB=OD ,
∴四边形 ABCD 是平行四边形,
∴AB∥CD,
∴ ∠FDO=∠EBO ,
∵ ∠FOD=∠EOB ,
∴△DOF≌△BOE(ASA),
∴ OF=OE ,
∴四边形 DEBF 是平行四边形,
∵ EF⊥BD ,
∴四边形 DEBF 是菱形;
(2)解:由(1)可得四边形 DEBF 是菱形,
∴ BE=BF ,
∵ AD//EF , EF⊥BD ,
∴ ∠ADB=90° ,
设 AD=x ,则 AB=12-x ,
∵ BD=43 ,
∴ AD2+BD2=AB2 ,即 x2+48=(12-x)2 ,
解得: x=4 ,
∴ AD=4,AB=8 ,
∴∠ABD=30°,∠DAB=60°,
∴ ∠FEB=∠DAB=60° ,
∴ △BEF 是等边三角形,
∴ ∠FBA=60° ,
∵ DE//BF ,
∴ ∠DEA=∠FBA=60° ,
∴ △BEF 是等边三角形,
∴ DE=AE=BF=BE ,
∴ ∠FAB=30° ,
∴ ∠AFB=90° ,
∴ AF=AB?cos∠FAB=43 .
22. (1)证明:∵四边形 PNQM 为菱形,
∴PM=NQ,BM // ND,
∵ PB=MP , QD=NQ ,
∴BM=ND,
∴四边形 BNDM 是平行四边形;
(2)解:∵四边形 BNDM 是平行四边形,
∴BM // ND,BM=ND,AD // BC,
∴∠NBM=∠CND,
∵ NC=BN ,
∴△BNM≌△NCD(SAS),
∴ ∠MNB=∠C ,
∵ DM=MA ,DM=BN,
∴ AD=BC ,
∴四边形 ABCD 是平行四边形,
∵ PM=BP=PN ,
∴ ∠PBN=∠PNB,∠PMN=∠PNM ,
∴由三角形内角和可得 ∠PNB+∠PNM=90° ,即 ∠MNB=90° ,
∴ ∠MNB=∠C=90° ,
∴四边形 ABCD 是矩形.
23.(1)解:证明: ∵ 四边形 ABCD 为菱形,
∴BC=CD ,
∵ 把线段 CE 绕点 C 顺时针旋转得到线段 CF ,
∴CE=CF ,
∵∠ECF=∠BCD ,
∴∠BCE=∠DCF ,
在 ΔBCE 与 ΔDCF 中,
{BC=CD∠BCE=∠DCFCE=CF ,
∴ΔBCE?ΔDCF(SAS) ,
∴BE=DF .
(2)∵ΔBCE?ΔDCF ,
∴BE=DF , ∠BEC=∠DFC ,
∵CB=CD ,
∴∠CBD=∠CDE ,
∵∠DFC=2∠CBD ,
∴∠BEC=2∠CDE ,
∵∠CEB=∠CDE+∠ECD ,
∴∠EDC=∠ECD ,
∴ED=EC=CF ,
∴BD=BE+EC=BE+CF=DF+DE=DF+CE=DF+CF .
24. (1)在 △ACD 中,点 O , E 分别为边 AC , AD 中点,
∴ OE 为 △ACD 的中位线
∴ OE//CD , OE=12CD
又∵ OE=12OF
∴ OF//CD , OF=CD
∴四边形 OCDF 为平行四边形
∴ FD//OC ,
{∠GFD=∠GCOFD=OC∠GDF=∠GOC ?
∴ △FGD≌△CGO (ASA)
(2)当 AB=12AC 时,四边形 FOCD 是菱形,
∵ AB=12AC
∵四边形 OCDF 为平行四边形,
∴ AB=CD ,
∴ CD=OC ,
∴四边形 FOCD 是菱形.
25. (1)证明:在△ABC中,∠B=90°,∠A=60°,∴∠C=30°,
∵DF⊥BC,∴∠DFC=90°
∵DC=2t,∴DF=t.
又∵AE=t,∴AE=DF;
∵∠B=∠DFC=90°,∴ AE∥DF
∴四边形AEFD是平行四边形
(2)解:能;
理由如下:
由(1)知,四边形AEFD为平行四边形.且∠C=30°
又∵AC=20,∴AD=AC-DC=20-2t,
若AE=AD,则平行四边形AEFD为菱形,
∴t=20-2t, ∴ t=203
(3)解:当t=5或8时,△DEF为直角三角形;
理由如下:
①∠EDF=90°时,四边形EBFD为矩形.
在Rt△AED中,∠ADE=∠C=30°,∴AD=2AE.即20-2t=2t,
∴t=5;
②∠DEF=90°时,∵四边形AEFD是平行四边形,
∴EF∥AD,∴∠ADE=∠DEF=90°.
∵在Rt△ADE中,∠A=60°,∴∠AED=30°,
∴AD= 12 AE,即20-2t= 12 t,∴t=8;
③∠EFD=90°时,此种情况不存在;
综上所述,当t=5或8时,△DEF为直角三角形
一、选择题
1.折叠矩形纸片ABCD,使点B落在点D处,折痕为MN,已知AB=8,AD=4,则MN的长是(?? )
A.?535???????????????????????????????B.?2 5????????????????????????C.?735?????????????????????????D.?4 5
2.将一张三角形纸片按如图步骤①至④折叠两次得图⑤,然后剪出图⑤中的阴影部分,则阴影部分展开铺平后的图形是(?? )
A.?等腰三角形????????????????????B.?直角三角形???????????????C.?矩形??????????????????D.?菱形
3.如图,已知点P是菱形 ABCD 的对角线 AC 延长线上一点,过点P分别作 AD 、 DC 延长线的垂线,垂足分别为点E、F.若 ∠ABC=120° , AB=2 ,则 PE-PF 的值为(?? )
A.?32???????????????????????????????B.?3???????????????????????????????C.?2??????????????????????????????????D.?52
4.如图,AC是菱形ABCD的对角线,P是AC上一个动点,过点P分别作AB、BC的垂线,垂足分别是F和E . 若菱形ABCD的周长是12cm,面积是6cm2 , 则PE+PF的值是(??? )
A.?1.5??????????????????????????????????????B.?1?????????????????????C.?2????????????????????????????????D.?4
5.如图,四边形 ABCD 是菱形,对角线 AC , BD 相交于点 O , AC=63 , BD=6 ,点 P 是 AC 上一动点,点 E 是 AB 的中点,则 PD+PE 的最小值为(??? )
A.?33??????????????????????????????B.?63???????????????????????????C.?3???????????????????????????D.?62
6.如图,在 △ABC 中, AB=AC , △DBC 和 △ABC 关于直线BC对称,连接AD , 与BC相交于点O , 过点C作 CE⊥CD ,垂足为C , 与AD相交于点E . 若 AD=8 , BC=6 ,则 2OE+AEBD 的值为(?? )
A.?43????????????????????????????B.?34???????????????C.?53?????????????????????????????D.?54
7.如图,在菱形 ABCD 中,按如下步骤作图:①分别以点C和点D为圆心,大于 12CD 长为半径作弧,两弧交于点 M、N ;②作直线 MN ,且 MN 恰好经过点A,与 CD 交于点E,连接 BE ,若 AD=6 ,则 BE 的长为(??? )
A.?37??????????????????????B.?33????????????????????????C.?4??????????????????????D.?25
8.如图,在菱形ABCD中,M,N分别在AB,CD上,且AM=CN,MN与AC交于点O,连接BO.若∠DAC=26°,则∠OBC的度数为(?? )
A.?54°???????????????????B.?64°???????????????????????????C.?74°????????????????????????D.?26°
9.如图,在菱形 ABCD 中,点 P 是对角线 BD 上一点, Q 是 BC 中点,若菱形周长是16, ∠A=120° ,则 PC+PQ 的最小值为(??? )
A.?2 3?????????????????????????B.?2??????????????????????????C.?3????????????????????????D.?33
10.如图1,点F从边长为5的菱形ABCD的顶点A出发,沿折线A-D-B以1cm/s的速度匀速运动到点B,点F运动时,△FBC的面积 y(cm2) 与时间 x(s) 之间的函数关系如图2所示,则 a 的值为(?? )
A.?8?????????????????????????B.?9?????????????????????????????C.?5+10?????????????????D.?5+23
二、填空题
11.如图,在菱形ABCD中,E,F分别在BC,DC上,BE=DF,AE=AB,若∠EAF=30°,则∠D的度数是________。
12.如图,在平行四边形ABCD中, AE平分∠BAD交BC于点E , 过点E作AE的垂线交CD于点F , 若CF=1,AD=5,则AB=________.
13.如图,四边形 ABCD 为菱形, ∠ABC=70° ,延长 BC 到 E ,在 ∠DCE 内作射线 CM ,使得 ∠ECM=15° ,过点 D 作 DF⊥CM ,垂足为 F ,若 DF=5 ,则对角线 BD 的长为________.(结果保留根号)
14.如图,在菱形 ABCD 中, ∠BAD=60° ,点E在边 BC 上,将 △ABE 沿直线 AE 翻折180°,得到 △AB'E ,点B的对应点是点 B' 若 AB'⊥BD , BE=2 ,则 BB' 的长是________.
15.已知菱形 ABCD 的面积为 23 ﹐点E是一边 BC 上的中点,点P是对角线 BD 上的动点.连接 AE ,若AE平分 ∠BAC ,则线段 PE 与 PC 的和的最小值为________,最大值为________.
16.如图,已知菱形ABCD的边长为6,点M是对角线AC上的一动点,目∠ABC=120°,则MA+MB+MD的最小值是________.
17.如图,矩形纸片ABCD中,AB=3,BC=5,将纸片折叠,使点B落在边AD的延长线上的点G处,折痕为EF,点E、F分别在边AD和边BC上.连接BG,交CD于点K,FG交CD于点H.给出以下结论:①EF⊥BG;②GE=GF;③DK=HK;④当点F与点C重合时 EF=10 .其中正确的结论是________(填写序号).
18.如图,在菱形ABCD中,AB=4,∠A=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为________.
三、解答题
19.如图, D 、 E 、 F 分别是 △ABC 各边的中点,连接 DE 、 EF 、 AE .
(1)求证:四边形 ADEF 为平行四边形;
(2)加上条件? ▲ ?后,能使得四边形 ADEF 为菱形,请从① ∠BAC=90° ;② AE 平分 ∠BAC ;③ AB=AC ,这三个条件中选择条件填空(写序号),并加以证明.
20.在菱形ABCD中,∠ADC=60°,点F为CD上任意一点(不与C、D重合),过点F作CD的垂线,交BD于点E,连结AE。
(1)①依题意补全图1;
②写出线段EF、CF、AE之间得等量关系,并说明理由;
(2)在图1中,将△DEF绕点D逆时针旋转,当F、E、C在一条直线上,如图2所示,请判断EF、CE、AE之间的等量关系,写出判断思路(可以不写出证明过程).
21.如图,在四边形 ABCD 中,对角线 AC 与 BD 交于点O,已知 OA=OC , OB=OD ,过点O作 EF⊥BD ,分别交 AB 、 DC 于点E,F,连接 DE , BF .
(1)求证:四边形 DEBF 是菱形:
(2)设 AD//EF , AD+AB=12 , BD=43 ,求 AF 的长.
22.如图,四边形 PNQM 为菱形,延长 MP 使得 PB=MP ,延长 NQ 使得 QD=NQ ,延长 BN 使得 NC=BN ,延长 DM 使得 DM=MA ,连接 AB , CD .
(1)求证:四边形 BNDM 是平行四边形.
(2)猜想:四边形 ABCD 是哪种特殊的四边形?并证明你的猜想.
23.四边形 ABCD 为菱形, BD 为对角线,在对角线 BD 上任取一点 E ,连接 CE ,把线段 CE 绕点 C 顺时针旋转得到线段 CF ,使得 ∠ECF=∠BCD ,点 E 的对应点为点 F ,连接 DF .
?
(1)如图1,求证: BE=DF ;
(2)如图2,若 ∠DFC=2∠DBC ,在不添加任何辅助线的前提下,请直接写出五对线段,使每对线段的和等于 BD ( BE 和 DE 除外).
24.已知:平行四边形 ABCD ,对角线 AC , BD 相交于点 O . E 是 AD 的中点,连接 OE 并延长至 F 使得 OE=EF ,连接 FD , FC , FC 交 BD 于点 G .
求证:
(1)△FGD≌△CGO .
(2)当 AB 与 AC 有怎样的数量关系时,四边形 FOCD 是菱形,并说明理由.
25.在Rt△ABC中,∠B=90°,AC =20,∠A=60°,点D从点C出发沿CA方向以每秒2个单位长的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动,设点D、E运动的时间是t秒(t>0),过点D作DF⊥BC于点F , 连接DE、EF .
(1)求证:四边形AEFD是平行四边形;
(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,说明理由;
(3)当t为何值时,△DEF为直角三角形?请说明理由.
答案
一、选择题
1.解:如图,连接BM,
由折叠可知,MN垂直平分BD,
∴OD=OB, ?
又AB∥CD,
∴∠MDO=∠NBO,∠DMO=∠BNO, ?
∴ △ BON≌ △ DOM,
∴ON=OM,
∴四边形BMDN为菱形(对角线互相垂直平分的四边形是菱形),
∴DN=BN=BM=DM, ?
设DN=NB=x,则AN=8﹣x,
在Rt △ ABD中,由勾股定理得:BD= AD2+AB2 = 45 ,
在Rt △ ADN中,由勾股定理得:AD2+AN2=DN2 ,
即42+(8﹣x)2=x2 ,
解得x=5,
根据菱形计算面积的公式,得
BN×AD= 12 ×MN×BD,
即5×4= 12 ×MN× 45 ,
解得MN= 25 .
故答案为:B.
2.如图,由题意可知,剪下的图形是四边形BACD,
由折叠的性质可知CA = AB,
∴△ABC是等腰三角形,
又∵△ABC和△BCD关于直线CD对称,
∴AB=BD=AC=CD,
∴四边形BACD是菱形,
故答案为:D.
3.解:∵四边形ABCD是菱形且∠ABC=120°,AB=2,
∴AB=BC=CD=DA=2,∠BAD=60°,AC⊥BD,
∴∠CAE=30?,
∵AC⊥BD,∠CAE=30°,AD=2,
∴AC= 222-12=23 ,
∴AP= 23 +PC,
在直角△AEP中,
∵∠PAE=30°,AP= 23 +PC,
∴PE= 12 AP= 3 + 12 PC,
在直角△PFC中,
∵∠PCF=30°,
∴PF= 12 PC,
∴ PE-PF = 3 + 12 PC- 12 PC= 3 ,
故答案为:B.
4.如图,连接PB
∵四边形ABCD是菱形,其周长为12cm
∴AB=BC=3cm, S△ABC=12S菱形=3 cm2
∵ S△PAB+S△PBC=S△ABC ,PF⊥AB , PE⊥BC
∴ 12AB·PF+12BC·PE=3
即PE+PF=2cm
故答案为:C.
5.解:如图,连接 DE ,
由两点之间线段最短得:当点 D,P,E 共线时, PD+PE 取最小值,最小值为 DE ,
∵ 四边形 ABCD 是菱形, AC=63 , BD=6 ,
∴AB=AD,OB=12BD=3,OA=12AC=33,AC⊥BD ,
∴AB=OA2+OB2=6 ,
∴AB=AD=BD=6 ,
∴△ABD 是等边三角形,
∵ 点 E 是 AB 的中点,
∴AE=12AB=3,DE⊥AB ,
∴DE=AD2-AE2=62-32=33 ,
即 PD+PE 的最小值为 33 ,
故答案为:A.
6.解:∵ AB=AC , △DBC 和 △ABC 关于直线BC对称,
∴AB=AC=CD=BD ,
∴四边形ABDC是菱形,
∴BC⊥AD,OC=OB,OA=OD,
∵ AD=8 , BC=6 ,
∴OC=OB=3,OA=OD=4,
在Rt△COD中,OC=3,OD=4,
∴DC= 32+42=5 ,
∴AB=AC=CD=BD =5,
∵ CE⊥CD ,
∴ CE2+CD2=DE2 , CE2=OE2+CO2 ,
∴ OE2+32+52=(OE+4)2 ,
∴ OE=94 ,
∴ 2OE+AEBD=OE+AE+OEBD=4+945=54 ,
故答案为:D .
7.解:根据作图,知AE是线段CD的垂直平分线,
∵四边形ABCD是菱形,
∴DE= 12 AD,∴∠DAE=30°,∠D=60°,∠BAE=90°,
在直角三角形ADE中,根据勾股定理,得AE= 62-32 = 33 ,
在直角三角形BAE中,根据勾股定理,得BE= 62+(33)2 = 37 .
故答案为:A.
8.∵四边形ABCD为菱形,
∴AB∥CD,AB=BC,
∴∠MAO=∠NCO,∠AMO=∠CNO,
在△AMO和△CNO中,
{∠MAO=∠NCOAM=CN∠AMO=∠CNO ,
∴△AMO≌△CNO(ASA),
∴AO=CO,
∵AB=BC,
∴BO⊥AC,
∴∠BOC=90°,
∵∠DAC=26°,
∴∠BCA=∠DAC=26°,
∴∠OBC=90°﹣26°=64°.
故答案为:B.
9.解:如图,由菱形的对称轴可知,点 A 和点 C 关于 BD 对称,连接 AQ , AQ 即为所求 PC+PQ 的最小值.
连接 AC ,
∵∠BAD=120° ,四边形 ABCD 是菱形,
∴∠ABC=60° , AB=BC ,
∴△ABC 是等边三角形,
∵ 点 Q 为 BC 的中点,
∴AQ⊥BC ,
∵ 菱形 ABCD 的周长为16,
∴AB=BC=4 ,
在 Rt△ABQ 中, ∠ABC=60° ,
∴∠BAQ=30° ,
∴BQ=12AB=12×4=2 ,
∴AQ=AB2-BQ2=42-22=23 .
故答案为:A.
10.解:过点D作DH⊥BC,如图:
∵菱形的边长为5,
∴ BC=5
当x=5时,y=7.5, y=12BC·DH
∴DH=3,
∴ CH=52-32=4 ,
∴ BH=5-4=1
Rt△BDH中,可得 BD=12+32=10 ,
∴AD+DB= 5+10
故答案为:C.
二、填空题
11.解:∵四边形ABCD是菱形,
∴AB=AD,∠B=∠D,
∵BE=FD,
∴△ABE≌△ADF(SAS),
∴AE=AF,∠BAE=∠DAF,
设∠B=x,∠BAE=y,
∵∠BAE+∠B+∠AEB=2x+y=180°,∠BAD+∠B=2y+x+30°=180°,
∴4x+2y-2y-x-30°=180°,
整理得3x=210°,
∴x=70°,
故答案为:70°.
12.过点E作EG//AB交AD于G,易得四边形ABCG是平行四边形,
又 AE平分∠BAD ,可得∠BAE=∠GAE=∠AEB,
∴AB=AE,四边形ABCG是菱形。
∴∠GBE=12∠ABE,AE⊥BG,
又AE⊥EF,故BG//EF。
∴∠GBE=∠FEC,
∵EG//AB,
∴∠BAE=∠GEC。
∴∠FEC=12∠GEC
故易得∠FEC=EFC。
∴EC=EF=1。
易得四边形ECDG是平行四边形。
可设AB=AG=x,
故GD=5-x,又EC=GD。
∴5-x=1,得x=4?
∴AB=4
13.解:连接AC,如图,
∵四边形ABCD是菱形,
∴AB//CD, ∠DOC=90° ,BD=2DO
∴ ∠DCE=∠ABC=70°
∵ ∠ECM=15°
∴ ∠DCM=55°
∵ DF⊥CM
∴ ∠CDF=35°
∵四边形ABCD是菱形,
∴ ∠CDB=12∠ADC=12∠ABC=35°
∴ ∠CDF=∠CDO
在 ΔCDO 和 ΔCDF 中,
{∠CDO=∠CDF∠COD=∠CFD=90°CD=CD ?
∴ ΔCDO ≌ ΔCDF
∴ DO=DF=5
∴ BD=2DO=25
故答案为: 25 .
14.解:∵四边形 ABCD 是菱形,
∴ AB=AD,AD//BC ,
∵ ∠BAD=60° ,
∴ ∠ABE=120° , △ABD 是等边三角形,即 ∠ABD=60° ,
∵ AB'⊥BD ,
∴ ∠BAB'=30° ,
由折叠的性质可得 ∠BAE=∠EAB'=15° , BE=B'E=2 , ∠BEA=∠B'EA ,
在 △BEA 中,由三角形内角和可得 ∠BEA=45° ,
∴ ∠BEA=∠B'EA=45° ,即 ∠BEB'=90° ,
∴ △BEB' 是等腰直角三角形,
∴ BB'=2BE=22 ;
故答案为 22 .
15.解:如图,连接 PC ,
∵ ? E 是 BC 的中点,AE平分 ∠BAC ,
∴AB=AC ,
∴ △ABC 是等腰三角形,
又 ∵ 四边形 ABCD 是菱形,则 AB=BC ,
∴ ? △ABC 是等边三角形,
∵ ?已知菱形 ABCD 的面积为 23 ,
设菱形的边长为 a (a>0)
则 AE=a2-(a2)2=32a ,
∵ ? S=BC×AE ?,
∴ ? 23=a×32a ,
解得: a=2 ,
∴AE=3 ?,
∵A、C 关于 BD 对称,
PE + PC =PE+PA ≥ AE =3 ,
则 PE + PC 最小值为: 3 ;
当点P与点D重合时 PE + PC 最大,
过E作 EH⊥BD 垂足为H,
∵ ?四边形 ABCD 是菱形,
∴EH//OC ,
∵ E 是 BC 的中点,
∴EH=12OC=14AC=12 ?,
OH=12OB=32 ?,
∴DH=DO+OH=323 ?,
在 Rt△DHE 中,DE=DH2+HE2
(323)2+(12)2=7 ,
则 DE+DC=2+7 ,
∴ PE + PC 最大为: 2+7 .
16.如图,作DE⊥AB于E点,连接BD,
∵菱形ABCD中,∠ABC=120°,
∴∠DAB=60°,则△ABD为等边三角形,
∴∠MAE=30°,
∴AM=2ME,
∵MD=MB,
∴MA+MB+MD=2ME+2MD=2DE,
根据垂线段最短,此时DE最短,即MA+MB+MD最小,
∵菱形的边长为6,
∴AB=6,AE=3,
∴ DE=AD2-AE2=33 ,
∴ 2DE=63 ,
∴MA+MB+MD最小值为 63 ,
故答案为: 63 .
17.解:连接BE,由折叠可知BO=GO,
∵EG//BF,
∴∠EGO=∠FBO,
在△EOG和△FOB中,
{∠EGO=∠FBO∠EOG=∠FOBBO=GO ,
∴△EOG≌△FOB(AAS) ,
∴EG=BF,
∴四边形EBFG是平行四边形,
由折叠可知BE=EG,
则四边形EBFG为菱形,
故EF⊥BG,GE=GF,
∴①②正确;
∵四边形EBFG为菱形,
过K作kM⊥FG于M,???????????????????????
∴KG平分∠DGH,KD⊥EG,
∴KD=KM,
在Rt△KMH中,KH为斜边,
∴KH > KM=KD,
∴③错误;
当点F与点C重合时,BE=BF=BC=5,AB=3,
在Rt△ABE中,由勾股定理AE= BE2-AB2=52-32=4 ,
∴ED=AD-AE=5-4=1,
在Rt△EDC中,由勾股定理EF= CD2+ED2=32+12=10 ,
∴④正确.
综合,正确的为①②④.
故答案为:①②④.
18.解:如图,作点P关于BD的对称点P′,作P′Q⊥CD交BD于K,交CD于Q,
则P′Q即为PK+QK的最小值,
作AE⊥CD交CD于E,易得AE=P′Q,
在菱形ABCD中,∵AB=4,∠A=120°,
所以AD=4,∠D=60°,
∴ AE=4×32=23
∴PK+QK的最小值为 23 .
三、解答题
19.(1)证明:已知 D 、 E 是 AB 、 BC 中点
∴ DE//AC
又∵ E 、 F 是 BC 、 AC 的中点
∴ EF//AB
∵ DE//AF
∴ EF//AD
∴四边形 ADEF 为平行四边形
(2)解:②或③;证明:选② AE 平分 ∠BAC
∵ AE 平分 ∠BAC
∴ ∠DAE=∠FAE
又∵平行四边形 ADEF
∴ EF//DA
∴ ∠FAE=∠AEF
∴ AF=EF
∴平行四边形 ADEF 是菱形
选③ AB=AC
∵ EF//AB 且 EF=12AB
DE//AC 且 DE=12AC
又∵ AB=AC
∴ EF=DE
∴平行四边形 ADEF 为菱形
故答案为:②或③
20. (1)解:①依题意补全图形如图所示:
②连接CE,
∵EF⊥CD
∴∠EFC=90°
∴CE=EF2+CF2
又∵四边形ABCD为菱形
∴BD⊥AC,BD平分AC
∴AE=CE
∴AE2=EF2+CF2
(2)EFCE、AE之间的等量关系是:AE-CE+2EF
判断:如图
延长EF至G,使EF=FG,连接DG
∴EG=2EF
∵DF⊥CF
∴DE=DG,∠EDG=2∠EDF
又∵四边形ABCD为菱形
∴AD=CD,∠ADC=2∠ODC=60°
又由旋转得∠ODC=∠EDF
∴∠ADC=∠EDG
∴∠ADE=2∠CDG
在△ADE和△CDG中 {AD=CD∠ADE=∠CDGDE=DG
∴△ADE≌△CDG
∴AE=CG=CE+EG=CE+2EF
∴AE=CE+2EF
21. (1)证明:∵ OA=OC , OB=OD ,
∴四边形 ABCD 是平行四边形,
∴AB∥CD,
∴ ∠FDO=∠EBO ,
∵ ∠FOD=∠EOB ,
∴△DOF≌△BOE(ASA),
∴ OF=OE ,
∴四边形 DEBF 是平行四边形,
∵ EF⊥BD ,
∴四边形 DEBF 是菱形;
(2)解:由(1)可得四边形 DEBF 是菱形,
∴ BE=BF ,
∵ AD//EF , EF⊥BD ,
∴ ∠ADB=90° ,
设 AD=x ,则 AB=12-x ,
∵ BD=43 ,
∴ AD2+BD2=AB2 ,即 x2+48=(12-x)2 ,
解得: x=4 ,
∴ AD=4,AB=8 ,
∴∠ABD=30°,∠DAB=60°,
∴ ∠FEB=∠DAB=60° ,
∴ △BEF 是等边三角形,
∴ ∠FBA=60° ,
∵ DE//BF ,
∴ ∠DEA=∠FBA=60° ,
∴ △BEF 是等边三角形,
∴ DE=AE=BF=BE ,
∴ ∠FAB=30° ,
∴ ∠AFB=90° ,
∴ AF=AB?cos∠FAB=43 .
22. (1)证明:∵四边形 PNQM 为菱形,
∴PM=NQ,BM // ND,
∵ PB=MP , QD=NQ ,
∴BM=ND,
∴四边形 BNDM 是平行四边形;
(2)解:∵四边形 BNDM 是平行四边形,
∴BM // ND,BM=ND,AD // BC,
∴∠NBM=∠CND,
∵ NC=BN ,
∴△BNM≌△NCD(SAS),
∴ ∠MNB=∠C ,
∵ DM=MA ,DM=BN,
∴ AD=BC ,
∴四边形 ABCD 是平行四边形,
∵ PM=BP=PN ,
∴ ∠PBN=∠PNB,∠PMN=∠PNM ,
∴由三角形内角和可得 ∠PNB+∠PNM=90° ,即 ∠MNB=90° ,
∴ ∠MNB=∠C=90° ,
∴四边形 ABCD 是矩形.
23.(1)解:证明: ∵ 四边形 ABCD 为菱形,
∴BC=CD ,
∵ 把线段 CE 绕点 C 顺时针旋转得到线段 CF ,
∴CE=CF ,
∵∠ECF=∠BCD ,
∴∠BCE=∠DCF ,
在 ΔBCE 与 ΔDCF 中,
{BC=CD∠BCE=∠DCFCE=CF ,
∴ΔBCE?ΔDCF(SAS) ,
∴BE=DF .
(2)∵ΔBCE?ΔDCF ,
∴BE=DF , ∠BEC=∠DFC ,
∵CB=CD ,
∴∠CBD=∠CDE ,
∵∠DFC=2∠CBD ,
∴∠BEC=2∠CDE ,
∵∠CEB=∠CDE+∠ECD ,
∴∠EDC=∠ECD ,
∴ED=EC=CF ,
∴BD=BE+EC=BE+CF=DF+DE=DF+CE=DF+CF .
24. (1)在 △ACD 中,点 O , E 分别为边 AC , AD 中点,
∴ OE 为 △ACD 的中位线
∴ OE//CD , OE=12CD
又∵ OE=12OF
∴ OF//CD , OF=CD
∴四边形 OCDF 为平行四边形
∴ FD//OC ,
{∠GFD=∠GCOFD=OC∠GDF=∠GOC ?
∴ △FGD≌△CGO (ASA)
(2)当 AB=12AC 时,四边形 FOCD 是菱形,
∵ AB=12AC
∵四边形 OCDF 为平行四边形,
∴ AB=CD ,
∴ CD=OC ,
∴四边形 FOCD 是菱形.
25. (1)证明:在△ABC中,∠B=90°,∠A=60°,∴∠C=30°,
∵DF⊥BC,∴∠DFC=90°
∵DC=2t,∴DF=t.
又∵AE=t,∴AE=DF;
∵∠B=∠DFC=90°,∴ AE∥DF
∴四边形AEFD是平行四边形
(2)解:能;
理由如下:
由(1)知,四边形AEFD为平行四边形.且∠C=30°
又∵AC=20,∴AD=AC-DC=20-2t,
若AE=AD,则平行四边形AEFD为菱形,
∴t=20-2t, ∴ t=203
(3)解:当t=5或8时,△DEF为直角三角形;
理由如下:
①∠EDF=90°时,四边形EBFD为矩形.
在Rt△AED中,∠ADE=∠C=30°,∴AD=2AE.即20-2t=2t,
∴t=5;
②∠DEF=90°时,∵四边形AEFD是平行四边形,
∴EF∥AD,∴∠ADE=∠DEF=90°.
∵在Rt△ADE中,∠A=60°,∴∠AED=30°,
∴AD= 12 AE,即20-2t= 12 t,∴t=8;
③∠EFD=90°时,此种情况不存在;
综上所述,当t=5或8时,△DEF为直角三角形
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
