福建省龙岩一高2021-2022学年高一上学期7月实验班选拔考试数学试题 PDF版含答案
文档属性
| 名称 | 福建省龙岩一高2021-2022学年高一上学期7月实验班选拔考试数学试题 PDF版含答案 |  | |
| 格式 | |||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-30 20:12:30 | ||
图片预览




文档简介
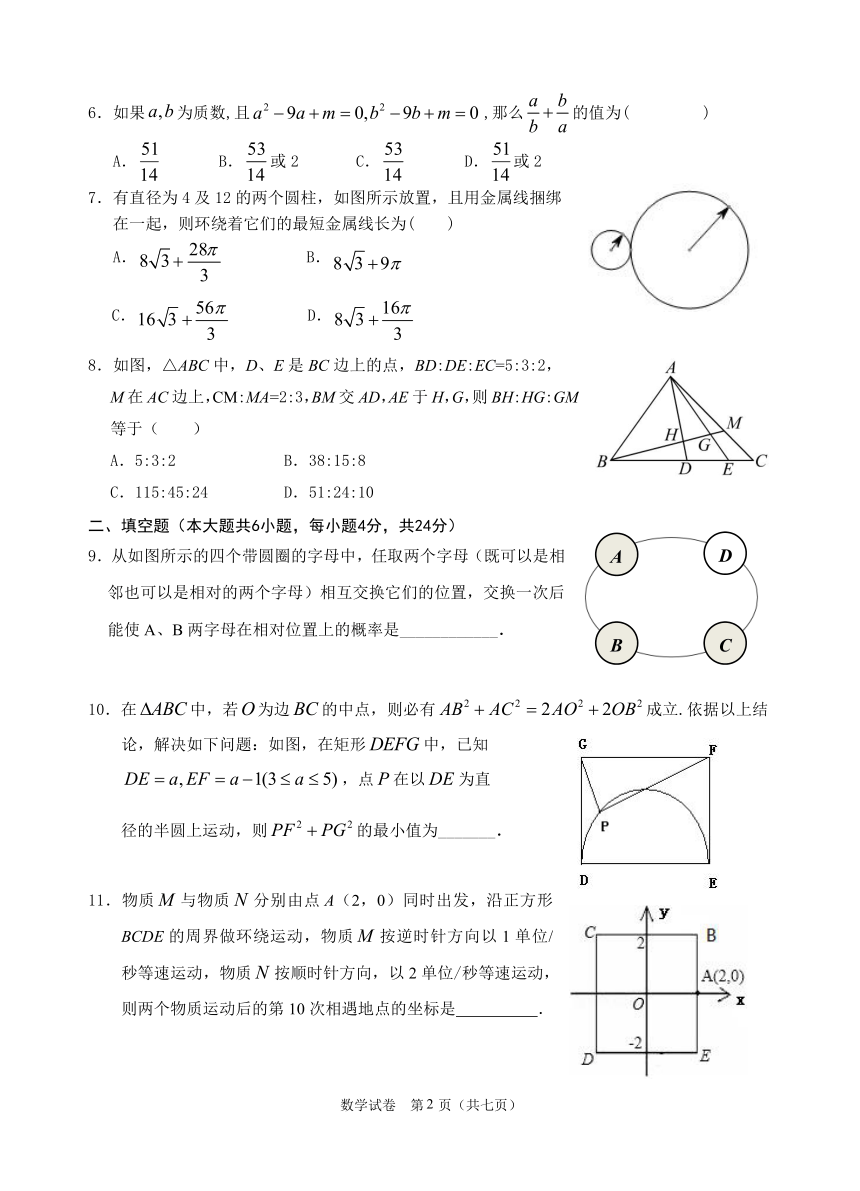
龙岩一中 2021 届高一实验班选拔考试
数 学
(考试时间:90 分钟 满分:100 分)
友情提示 :请 将答 案填写在 答题 卷中 ,写 在试 卷上不得 分.
一、选择题(本大题共8小题,每小题3分,共24分,在给出的四个选项中,只有一项是符合
题目要求的)
1
1.若 3 3
b?1?a?b,则a?b,(a?b) , a?b, 一定是( )
a?b
1
A. 最小, 3 3
(a?b) 最大 B. a?b最小,a?b最大
a?b
1 1
C. 最小, 3
a?b最大 D. 最小, a?b最大
a?b a?b
2.如图1,在等边△ABC中,D是BC的中点, y
P为AB边上的一个动点,设AP=x,图1中
线段DP的长为y,若表示y与x的函数关系 3
的图象如图2所示,则△ABC的面积为( ) 2
3
A. B.1 C. 3 D.3 O x
2
图1 图2
3.如图,是一个带有方形空洞和圆形空洞的儿童玩具,如果用下列几何体作为塞子,那么既可
以堵住方形空洞,又可以堵住圆形空洞的几何体是( )
A. B. C. D.
?x?a?3
4.若关于x的不等式组? 有解,则函数 2
y ?(a?4)x ?2x?1图象与x轴的交点个数
?x?3a?3
为( )
A.2 B.1或2 C.1 D.0
5.满足等式x y ? y x? 19x? 19y ? 19xy ?19的正整数对(x,y)的个数是( )
A. 19 B. 18 C.1 D.2
数学试卷 第1页(共七页)
a b
6.如果a,b为质数,且 2 2
a ?9a?m?0,b ?9b?m?0 ,那么 ? 的值为( )
b a
51 53 53 51
A. B 2 C 2
14 14 14 14
7412
( )
A 28?
8 3? 8 3?9?
3
56? 16?
16 3 ? ?8 3?
3 3
ABCDEBCBDDEEC=532
MACCMMA=23BMADAEHGBHHGGM
A B
C D
二、填空题(本大题共6小题,每小题4分,共24分)
A D
二合
AB____________. B C
.?ABC中,若O为边BC的中点,则必有 2 2 2 2
AB ? AC ?2AO ?2OB 成立.依据以上结
论,解决如下问题:如图,在矩形DEFG
DE ?a,EF ??1(3??5),点PDE
2 2
PF ?PG .
11.物质M 与物质N A(2,0)同时出发,沿正方形
BCDE M 1 单位/
N 2单位/秒等速运动,
则两个物质运动后的第10
数学试卷 第2页(共七页)
12.已知关于 4 3 2
x的方程x ?2x ?(3?k)x ?(2?k)x?2k ?0 有实根.若所有实根的平方和为7,
则所有实根之积为_______.
13.如图,直径为ABOPQPCABCQDAB
DQEOPEAC8DE12O______
2
14a是正整数,且a ?60a是一个正整数的平方,则a的最大值为_______.
三、解答题(本大题共5小题,共52分)
15.(本题8分)
2 ? ?
先化简,再求值: 2 x x 2 2
x ?2x?1? 2 ?( ?1),其中x ? 3?1.
x ?1 x?1
16.(本题10分)
如 图 ,在 △ABC中,I是 内心,O是AB边上一点,圆O经 过B点
且与AI相切 于I点.
(1ABC
2BC=18O5AI
A A
A
y ( 千人) 与门 票价格 x ( 元/人 )
(10? x?50)的 关系如图 所示,其中 AB为反比
例 函 数 图象 的 一 部 分,BC 为一次 函数 图 象的 一部
分 .设该 公司经营景区A的年利润 为z(万 元).
(1)求出每年的游客量 y(千人)与x(元/
人)之间的函数关系式;
(2)利用第一年该公司经营景区A的年利润
z (万元)与x(元/人)之间的函数关系式,求
出第一年年利润的最大值.
数学试卷 第3页(共七页)
18.(本题10分)
当?1? x?1时,函数 2
y ? ?x ?2ax?b?1的最小值是?4,最大值是0,求a、b的值.
19.(本题14分)
如图,抛物线 2
y ?ax ?bx过 A(4,0),B(1,3)两点,点C、B关于抛物线的对称轴对称,过
3
点B作直线BH ? x轴,交x轴于点H ,点E( ,0).
2
( 1)已 知在 抛物 线的对称轴上有一点F ,使得?BEF 的周长最小,请求出点F 的坐标(注:
只要能求出点F 的坐标即可,不要求证明);
(2)点P是抛物线上一动点,且位于第四象限,当?ABP的面积为15时,求出点P的坐
标;
(3)若点M 在直线BH 上运动,点N 在x轴上运动,当以点C、M、N 为顶点的三角形
为等腰直角三角形时,请直接写出此时点N 的坐标.
数学试卷 第4页(共七页)
龙岩一中 2021 届高一实验班选拔考试
数学答题卷
一、选择题(每小题3分,共8题,在给出的四个选项中,只有一项是符合题目要求的)
题号 1 2 3 4 5 6 7 8
答案
二、填空题(每小题4分,共6小题)
9. ;10. ;11. ;
12. ;13. ;14. ;
三、解答题(共5小题,共52分)
15.(本题8分)
16.(本题10分)
数学试卷 第5页(共七页)
17.(本题10分)
18.(本题10分)
数学试卷 第6页(共七页)
19.(本题14分)
数学试卷 第7页(共七页)
龙岩一中 2021 届高一实验班选拔考试
数学参考答案
一、选择题(每小题3分,共8题,在给出的四个选项中,只有一项是符合题目要求的)
题号 1 2 3 4 5 6 7 8
答案 A C D B D B A C
二、填空题(本大题共6小题,每小题4分,共24分)
1 4
9. 10. 5 11. (? ,2) 12. -3 13. 26 14.196
3 3
三、解答题(本大题共5小题,共52分)
15.(本题8分)
(x?2)(x?1) 1?x x?2 3?1
x?1? ? ? x?1? ?2? 3?
解:原式= (x?1)(x?1) x?1 1?x 2? 3 …………………8分
?2? 3?5?3 3 ?7?2 3
16.(本题10分)
解:(1ABCAIBCDOI
IABCBIABCOBI=DBI
OB=OIOBI=OIBDBI=OIBOIBD
AIOOIAIBDAD
AI平分∠BAC,∴AB=AC,∴△ABC为等腰三角形;………………5分
AO OI AI AB?5 5 45
(2)∵OI∥BC,∴△AOI∽△ABD,∴ ? ? ,∴ ? ,∴AB= ,
AB BD AD AB 9 4
27 OI 5 27 15
∴ 2 2
AD= AB ?BD ? ,∴AI= ?AD= ? = .…………………10分
4 BD 9 4 4
17.(本题10分)
k 1600
解:(1)当10? x?20时,设y ? ,将A(10,160)代入得k ?1600,所以 y ? ;
x x
?a ??2
当20? x?50时,设 y ?ax?b,将B(20,80),C(50,20)代入得? ,
?b?120
所以 y ? ?2x?1 2 0, ………5分
数学试卷 第8页(共七页)
1600 1 1600
(2)当10? x?20时, y ? ,此时,z ?(x?10)y? ?50?10?? ?100,z随
x 10 x
x的增大而增大,所以当x?20时,zmax ?20万元;
1 1
当 2
20? x?50时, y ??2x?120,z ?(x?10)y? ?50?10? (?x ?70x?900),
10 5
所以当x?35时,zmax ?65万元;
因为65?20,所以当门票价格定为35元/人时,第一年年利润的最大值为65万元.…10分
18.(本 题 10分)
2
解: 2 2
y ? ?x ?2ax?b?1? ??x?a? ?a ?b?1,其对称轴为直线x ? ?a,
??1?2a?b?1? ?4 ? a ?1
①当 ?a ? ?1,即a ?1时,? ,解得? . …………………2分
? ?1?2a?b?1? 0 ?b ? ?2
2
? a ?b?1? 0
②当 2
?1??a?0,即0?a?1时, ? 消去b得,a ?2a?3?0,
??1?2a?b?1? ?4
解得a ?1或a ? ?3,舍去. …………………4分
2
? a ?b?1? 0
③当 2
0? ?a ?1,即?1? a ?0时,? 消去b得,a ?2a?3?0
??1?2a?b?1? ?4
解得a ? ?1或a ?3,舍去. …………………6分
? ?1?2a?b?1? 0 ?a ? ?1
④当 ?a ?1,即a??1时,? 解得? …………………8分
??1?2a?b?1? ?4 ?b ? ?2
综上所述a ?1,b ? ?2或a ? ?1,b ? ?2 . ………………10分
19.(本题14分)
解:(1)把点A(4,0),B(1,3)代入抛物线 2
y ?ax ?bx中,
?0?16a?4b ?a??1
得? ,解得? ,∴抛物线表达式为 2
y ??x ?4x;………………… 2分
?3?a?b ?b?4
所以该抛物线的对称轴为直线x=2,∴B、C两点关于对称轴x=2成轴对称,C(3,3),
数学试卷 第9页(共七页)
?y ?2x?3 ?x?2
∴直线CE为y=2x-3 ∴? ,解得? y
?x?2 ?y ?1
B C
?BEF F (2,1). 5
2
21BBP(m,?m ?4m) O H A x
2
??HD?m ?4mPD?m?1
S△ABP=S△ABH+S四边形HAPD﹣S△BPD,
1 1 1 D P
∴ 2 2
15? ?3?3? (3?m?1)(m ?4m)? (m?1)(3?m ?4m)
2 2 2 图1
2
3m ?15m?18?0,解得m1 ??1(舍去),m2 ?6,∴点P坐标为(6,?12);………10分
( 3)当△CMN 为等 腰直 角三 角形时N点坐标为( 2, 0)或(﹣4, 0)或 (﹣2, 0)或 (4,0).
…………………14分
数学试卷 第10页(共七页)
数 学
(考试时间:90 分钟 满分:100 分)
友情提示 :请 将答 案填写在 答题 卷中 ,写 在试 卷上不得 分.
一、选择题(本大题共8小题,每小题3分,共24分,在给出的四个选项中,只有一项是符合
题目要求的)
1
1.若 3 3
b?1?a?b,则a?b,(a?b) , a?b, 一定是( )
a?b
1
A. 最小, 3 3
(a?b) 最大 B. a?b最小,a?b最大
a?b
1 1
C. 最小, 3
a?b最大 D. 最小, a?b最大
a?b a?b
2.如图1,在等边△ABC中,D是BC的中点, y
P为AB边上的一个动点,设AP=x,图1中
线段DP的长为y,若表示y与x的函数关系 3
的图象如图2所示,则△ABC的面积为( ) 2
3
A. B.1 C. 3 D.3 O x
2
图1 图2
3.如图,是一个带有方形空洞和圆形空洞的儿童玩具,如果用下列几何体作为塞子,那么既可
以堵住方形空洞,又可以堵住圆形空洞的几何体是( )
A. B. C. D.
?x?a?3
4.若关于x的不等式组? 有解,则函数 2
y ?(a?4)x ?2x?1图象与x轴的交点个数
?x?3a?3
为( )
A.2 B.1或2 C.1 D.0
5.满足等式x y ? y x? 19x? 19y ? 19xy ?19的正整数对(x,y)的个数是( )
A. 19 B. 18 C.1 D.2
数学试卷 第1页(共七页)
a b
6.如果a,b为质数,且 2 2
a ?9a?m?0,b ?9b?m?0 ,那么 ? 的值为( )
b a
51 53 53 51
A. B 2 C 2
14 14 14 14
7412
( )
A 28?
8 3? 8 3?9?
3
56? 16?
16 3 ? ?8 3?
3 3
ABCDEBCBDDEEC=532
MACCMMA=23BMADAEHGBHHGGM
A B
C D
二、填空题(本大题共6小题,每小题4分,共24分)
A D
二合
AB____________. B C
.?ABC中,若O为边BC的中点,则必有 2 2 2 2
AB ? AC ?2AO ?2OB 成立.依据以上结
论,解决如下问题:如图,在矩形DEFG
DE ?a,EF ??1(3??5),点PDE
2 2
PF ?PG .
11.物质M 与物质N A(2,0)同时出发,沿正方形
BCDE M 1 单位/
N 2单位/秒等速运动,
则两个物质运动后的第10
数学试卷 第2页(共七页)
12.已知关于 4 3 2
x的方程x ?2x ?(3?k)x ?(2?k)x?2k ?0 有实根.若所有实根的平方和为7,
则所有实根之积为_______.
13.如图,直径为ABOPQPCABCQDAB
DQEOPEAC8DE12O______
2
14a是正整数,且a ?60a是一个正整数的平方,则a的最大值为_______.
三、解答题(本大题共5小题,共52分)
15.(本题8分)
2 ? ?
先化简,再求值: 2 x x 2 2
x ?2x?1? 2 ?( ?1),其中x ? 3?1.
x ?1 x?1
16.(本题10分)
如 图 ,在 △ABC中,I是 内心,O是AB边上一点,圆O经 过B点
且与AI相切 于I点.
(1ABC
2BC=18O5AI
A A
A
y ( 千人) 与门 票价格 x ( 元/人 )
(10? x?50)的 关系如图 所示,其中 AB为反比
例 函 数 图象 的 一 部 分,BC 为一次 函数 图 象的 一部
分 .设该 公司经营景区A的年利润 为z(万 元).
(1)求出每年的游客量 y(千人)与x(元/
人)之间的函数关系式;
(2)利用第一年该公司经营景区A的年利润
z (万元)与x(元/人)之间的函数关系式,求
出第一年年利润的最大值.
数学试卷 第3页(共七页)
18.(本题10分)
当?1? x?1时,函数 2
y ? ?x ?2ax?b?1的最小值是?4,最大值是0,求a、b的值.
19.(本题14分)
如图,抛物线 2
y ?ax ?bx过 A(4,0),B(1,3)两点,点C、B关于抛物线的对称轴对称,过
3
点B作直线BH ? x轴,交x轴于点H ,点E( ,0).
2
( 1)已 知在 抛物 线的对称轴上有一点F ,使得?BEF 的周长最小,请求出点F 的坐标(注:
只要能求出点F 的坐标即可,不要求证明);
(2)点P是抛物线上一动点,且位于第四象限,当?ABP的面积为15时,求出点P的坐
标;
(3)若点M 在直线BH 上运动,点N 在x轴上运动,当以点C、M、N 为顶点的三角形
为等腰直角三角形时,请直接写出此时点N 的坐标.
数学试卷 第4页(共七页)
龙岩一中 2021 届高一实验班选拔考试
数学答题卷
一、选择题(每小题3分,共8题,在给出的四个选项中,只有一项是符合题目要求的)
题号 1 2 3 4 5 6 7 8
答案
二、填空题(每小题4分,共6小题)
9. ;10. ;11. ;
12. ;13. ;14. ;
三、解答题(共5小题,共52分)
15.(本题8分)
16.(本题10分)
数学试卷 第5页(共七页)
17.(本题10分)
18.(本题10分)
数学试卷 第6页(共七页)
19.(本题14分)
数学试卷 第7页(共七页)
龙岩一中 2021 届高一实验班选拔考试
数学参考答案
一、选择题(每小题3分,共8题,在给出的四个选项中,只有一项是符合题目要求的)
题号 1 2 3 4 5 6 7 8
答案 A C D B D B A C
二、填空题(本大题共6小题,每小题4分,共24分)
1 4
9. 10. 5 11. (? ,2) 12. -3 13. 26 14.196
3 3
三、解答题(本大题共5小题,共52分)
15.(本题8分)
(x?2)(x?1) 1?x x?2 3?1
x?1? ? ? x?1? ?2? 3?
解:原式= (x?1)(x?1) x?1 1?x 2? 3 …………………8分
?2? 3?5?3 3 ?7?2 3
16.(本题10分)
解:(1ABCAIBCDOI
IABCBIABCOBI=DBI
OB=OIOBI=OIBDBI=OIBOIBD
AIOOIAIBDAD
AI平分∠BAC,∴AB=AC,∴△ABC为等腰三角形;………………5分
AO OI AI AB?5 5 45
(2)∵OI∥BC,∴△AOI∽△ABD,∴ ? ? ,∴ ? ,∴AB= ,
AB BD AD AB 9 4
27 OI 5 27 15
∴ 2 2
AD= AB ?BD ? ,∴AI= ?AD= ? = .…………………10分
4 BD 9 4 4
17.(本题10分)
k 1600
解:(1)当10? x?20时,设y ? ,将A(10,160)代入得k ?1600,所以 y ? ;
x x
?a ??2
当20? x?50时,设 y ?ax?b,将B(20,80),C(50,20)代入得? ,
?b?120
所以 y ? ?2x?1 2 0, ………5分
数学试卷 第8页(共七页)
1600 1 1600
(2)当10? x?20时, y ? ,此时,z ?(x?10)y? ?50?10?? ?100,z随
x 10 x
x的增大而增大,所以当x?20时,zmax ?20万元;
1 1
当 2
20? x?50时, y ??2x?120,z ?(x?10)y? ?50?10? (?x ?70x?900),
10 5
所以当x?35时,zmax ?65万元;
因为65?20,所以当门票价格定为35元/人时,第一年年利润的最大值为65万元.…10分
18.(本 题 10分)
2
解: 2 2
y ? ?x ?2ax?b?1? ??x?a? ?a ?b?1,其对称轴为直线x ? ?a,
??1?2a?b?1? ?4 ? a ?1
①当 ?a ? ?1,即a ?1时,? ,解得? . …………………2分
? ?1?2a?b?1? 0 ?b ? ?2
2
? a ?b?1? 0
②当 2
?1??a?0,即0?a?1时, ? 消去b得,a ?2a?3?0,
??1?2a?b?1? ?4
解得a ?1或a ? ?3,舍去. …………………4分
2
? a ?b?1? 0
③当 2
0? ?a ?1,即?1? a ?0时,? 消去b得,a ?2a?3?0
??1?2a?b?1? ?4
解得a ? ?1或a ?3,舍去. …………………6分
? ?1?2a?b?1? 0 ?a ? ?1
④当 ?a ?1,即a??1时,? 解得? …………………8分
??1?2a?b?1? ?4 ?b ? ?2
综上所述a ?1,b ? ?2或a ? ?1,b ? ?2 . ………………10分
19.(本题14分)
解:(1)把点A(4,0),B(1,3)代入抛物线 2
y ?ax ?bx中,
?0?16a?4b ?a??1
得? ,解得? ,∴抛物线表达式为 2
y ??x ?4x;………………… 2分
?3?a?b ?b?4
所以该抛物线的对称轴为直线x=2,∴B、C两点关于对称轴x=2成轴对称,C(3,3),
数学试卷 第9页(共七页)
?y ?2x?3 ?x?2
∴直线CE为y=2x-3 ∴? ,解得? y
?x?2 ?y ?1
B C
?BEF F (2,1). 5
2
21BBP(m,?m ?4m) O H A x
2
??HD?m ?4mPD?m?1
S△ABP=S△ABH+S四边形HAPD﹣S△BPD,
1 1 1 D P
∴ 2 2
15? ?3?3? (3?m?1)(m ?4m)? (m?1)(3?m ?4m)
2 2 2 图1
2
3m ?15m?18?0,解得m1 ??1(舍去),m2 ?6,∴点P坐标为(6,?12);………10分
( 3)当△CMN 为等 腰直 角三 角形时N点坐标为( 2, 0)或(﹣4, 0)或 (﹣2, 0)或 (4,0).
…………………14分
数学试卷 第10页(共七页)
同课章节目录
