第6章 平面图形的认识(一)单元检测题(含解析)
文档属性
| 名称 | 第6章 平面图形的认识(一)单元检测题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 264.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-31 16:43:01 | ||
图片预览



文档简介
初中数学苏科版七年级上册第六章 平面图形的认识(一) 同步测试卷
一、单选题
1.下列说法正确的是( ??)
A.?具有公共顶点的两个角是对顶角
B.?A,B 两点之间的距离就是线段 AB
C.?两点之间,线段最短
D.?不相交的两条直线叫做平行线
2.下列说法不正确的是(?? )
A.?对顶角相等??????????B.?两点确定一条直线??????????C.?一个角的补角一定大于这个角??????????D.?垂线段最短
3.下列说法错误的是(?? )
A.?平面内过一点有且只有一条直线与已知直线平行
B.?平面内过一点有且只有一条直线与已知直线垂直
C.?两点之间的所有连线中,线段最短
D.?对顶角相等
4.如图,∠ACB=90°,CD⊥AB,D为垂足.下列判断错误的是(?? )
A.?∠A=∠B????????????????????????????B.?∠A=∠BCD ??C.?AC>AD????????????????????????????D.?BC>CD
5.如图,已知点A是射线BE上一点,过A作AC⊥BF,垂足为C,CD⊥BE,垂足为D.给出下列结论:①∠1是∠ACD的余角;②图中互余的角共有3对;③∠1的补角只有∠DCF;④与∠ADC互补的角共有3个.其中正确结论有(? )
A.?①????????????????????????????????????B.?①②③????????????????????????????????????C.?①④????????????????????????????????????D.?②③④
6.下列时刻中,时针与分针所成的角(小于平角)最大的是(?? )
A.?9:00?????????????????????????????????B.?3:30?????????????????????????????????C.?6:40?????????????????????????????????D.?5:45
二、填空题
7.已知直线 AB 与直线 CD 相交于点 O , EO⊥CD ,垂足为 O .若 ∠AOC=25°12′ ,则 ∠BOE 的度数为________.(单位用度表示)
8.如图,直线AB与CD相交于点O , OM⊥AB ,若 ∠DOM=55° ,则 ∠AOC =________°.
9.G101是一班从北京南站开往上海虹桥的下行(单向)高速列车,停靠如图所示的11个站点,则该趟列车共有________个乘车区间(指旅客乘车地与目的地之间的区间).
10.数轴上有点A和点B,点A到原点的距离为m,点B到原点的距离为n,且点B在点A的左边,若m<n,则点A与点B的距离等于________.
11.数轴上A点表示的数为-2,则A点相距3个单位长度的点表示的数是________
12.数轴上表示有理数﹣5.5与3.5两点的距离是________.
13.在平面直角坐标系中,若点M(﹣2,3)与点N(x,3)之间的距离是5,则x的值是________.
14.已知 ∠α 与 ∠β 互为余角, ∠α=38?24' ,则 ∠β= ________.
15.如图,已知 OC⊥OA,OD⊥OB .若 ∠AOB=148° ,则 ∠COD= ________.
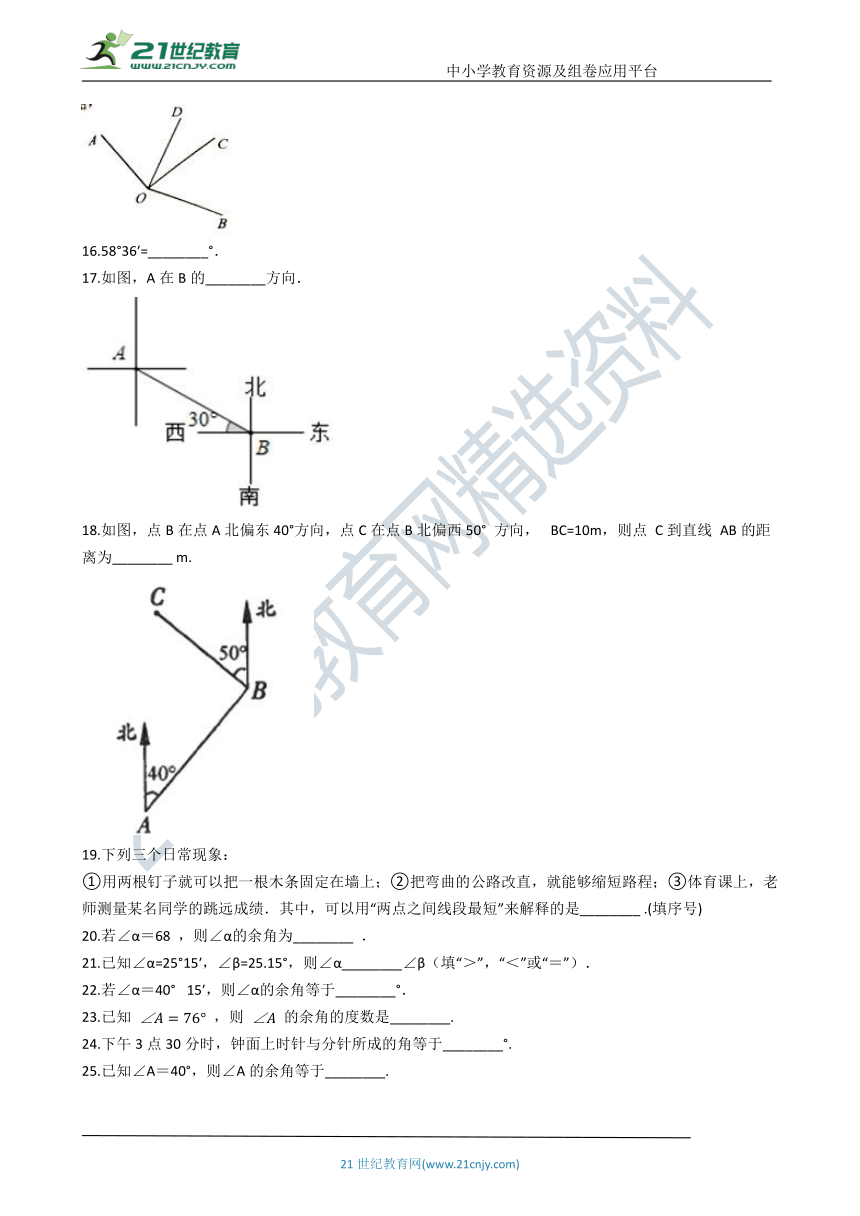
16.58°36′=________°.
17.如图,A在B的________方向.
18.如图,点B在点A北偏东40°方向,点C在点B北偏西50° 方向,? BC=10m,则点 C到直线 AB的距离为________ m.
19.下列三个日常现象:
①用两根钉子就可以把一根木条固定在墙上;②把弯曲的公路改直,就能够缩短路程;③体育课上,老师测量某名同学的跳远成绩.其中,可以用“两点之间线段最短”来解释的是________ .(填序号)
20.若∠α=68 ,则∠α的余角为________ .
21.已知∠α=25°15′,∠β=25.15°,则∠α________∠β(填“>”,“<”或“=”).
22.若∠α=40°? 15′,则∠α的余角等于________°.
23.已知 ∠A=76° ,则 ∠A 的余角的度数是________.
24.下午3点30分时,钟面上时针与分针所成的角等于________°.
25.已知∠A=40°,则∠A的余角等于________.
26.北京时间上午5点整,时针与分针所成的角的度数是________.
27.已知∠α=28°,则∠α的补角为________°.
三、计算题
28.???
(1)?314?(?114)?(?223+23)
(2)?12?|?8|+(?2)3+(118?43)×24
(3)42°15′26″×4?21°36′20″÷5+3.295°
29.计算:
(1)﹣22÷23﹣(﹣23)×(﹣3)2
(2)16°51′+38°27′×3﹣35°29′.
四、作图题
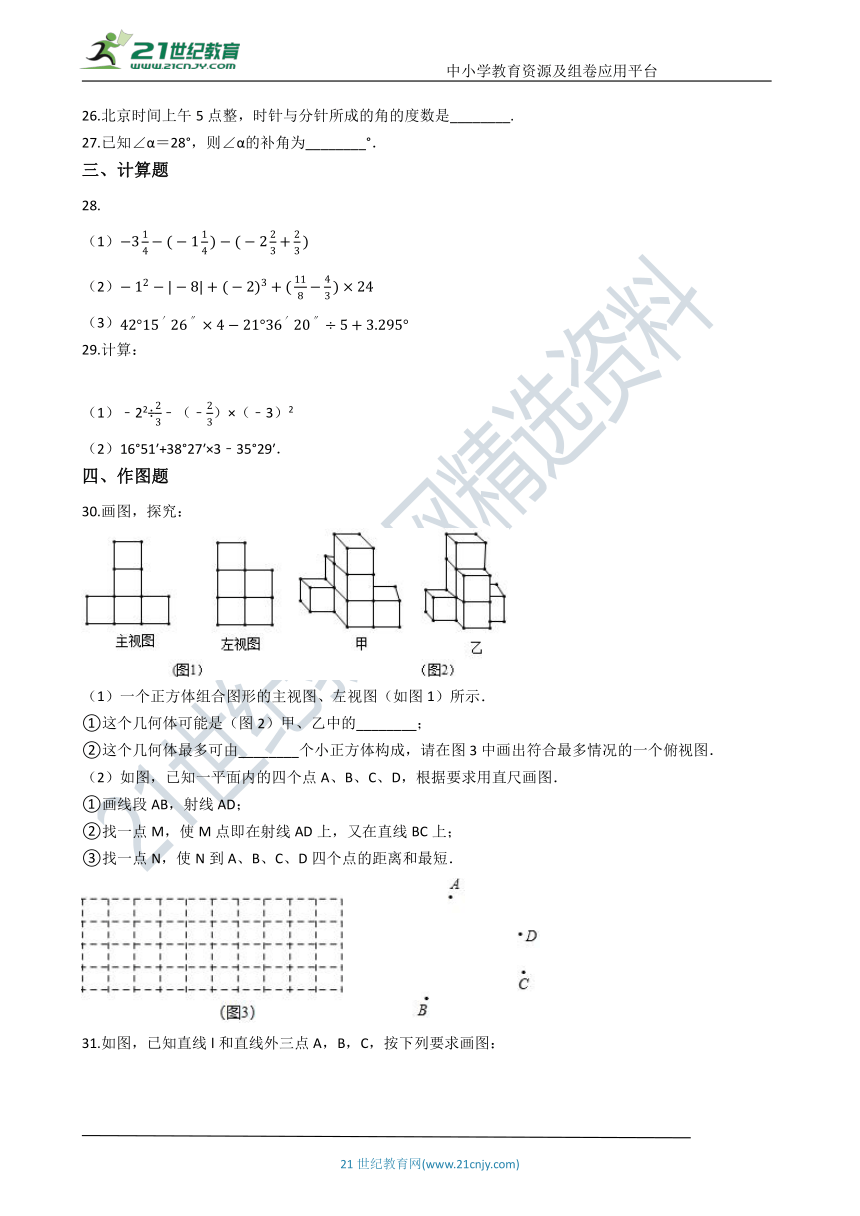
30.画图,探究:
(1)一个正方体组合图形的主视图、左视图(如图1)所示.
①这个几何体可能是(图2)甲、乙中的________;
②这个几何体最多可由________个小正方体构成,请在图3中画出符合最多情况的一个俯视图.
(2)如图,已知一平面内的四个点A、B、C、D,根据要求用直尺画图.
①画线段AB,射线AD;
②找一点M,使M点即在射线AD上,又在直线BC上;
③找一点N,使N到A、B、C、D四个点的距离和最短.
31.如图,已知直线l和直线外三点A,B,C,按下列要求画图:
①画射线CB交直线l于点F;
②连接BA;
③在直线l上确定点E,使得AE+CE最小.
五、综合题
32.有一科技小组进行了机器人行走性能试验,在试验场地有A、B、C三点顺次在同一笔直的赛道上,A、B两点之间的距离是90米,甲、乙两机器人分别从A、B两点同时同向出发到终点C,乙机器人始终以50米分的速度行走,乙行走9分钟到达C点.设两机器人出发时间为t(分钟),当t=3分钟时,甲追上乙.
请解答下面问题:
(1)B、C两点之间的距离是________米.
(2)求甲机器人前3分钟的速度为多少米/分?
(3)若前4分钟甲机器人的速度保持不变,在4≤t≤6分钟时,甲的速度变为与乙相同,求两机器人前6分钟内出发多长时间相距28米?
(4)若6分钟后甲机器人的速度又恢复为原来出发时的速度,直接写出当t>6时,甲、乙两机器人之间的距离S.(用含t的代数式表示).
33.阅读下面材料:如图,点A、B在数轴上分别表示有理数a、b,则A、B两点之间的距离可以表示为|a?b|.
根据阅读材料与你的理解回答下列问题:
(1)数轴上表示3与?2的两点之间的距离是________.
(2)数轴上有理数x与有理数7所对应两点之间的距离用绝对值符号可以表示为________.
(3)代数式|x+8|可以表示数轴上有理数x与有理数________?所对应的两点之间的距离;若|x+8|=5,则x=________.
(4)求代数式|x+2018|+|x+504|+|x?2017|的最小值.
34.已知数轴上有A、B、C三点,分别代表-24,-10,10,两只电子蚂蚁甲、乙分别从A、C两点同时相向而行,甲的速度为4个单位/秒,乙的速度为6个单位/秒.
(1)甲、乙多少秒后相遇?
(2)甲出发多少秒后,甲到A、B、C三点的距离和为40个单位?
(3)当甲到A、B、C三点的距离和为40个单位时,甲调头返回,当甲、乙在数轴上再次相遇时,相遇点表示的数是________.
35.如图,已知数轴上有A、B、C三个点,它们表示的数分别是18,8,﹣10.
(1)填空:AB=________,BC=________;
(2)若点A以每秒1个单位长度的速度向右运动,同时,点B和点C分别以每秒2个单位长度和5个单位长度的速度向左运动.试探索:BC﹣AB的值是否随着时间t的变化而改变?请说明理由.
(3)现有动点P、Q都从A点出发,点P以每秒1个单位长度的速度向终点C移动;当点P移动到B点时,点Q才从A点出发,并以每秒3个单位长度的速度向左移动,且当点P到达C点时,点Q就停止移动.设点P移动的时间为t秒,试用含t的代数式表示P、Q两点间的距离.
36.阅读下面材料:
若点A、B在数轴上分别表示数a,b,则A、B两点之间的距离表示为|AB|
(1)数轴上表示2和5两点之间的距离是________,数轴上表示-3和4两点之间的距离是________.
(2)若数轴上点B表示的数是-1,且|AB| = 3,则a=________.
(3)在数轴上有三个点A, B, C若点A表示的数是-1,点B表示的数是3,且|AB| + |AC| = 6 ,求点C表示的数.
37.已知在纸面上有一数轴 ( 如图 ) ,折叠纸面:
(1)若1表示的点与-1表示的点重合,则 ?2 表示的点与数________表示的点重合;
(2)若-1表示的点与5表示的点重合,回答以下问题:
①6表示的点与数________表示的点重合;
②若数轴上A、B两点之间的距离为 11(A 在B的左侧 ) ,且A、B两点经折叠后重合,求A、B两点表示的数是多少?________
38.如图,点P、Q在数轴上表示的数分别是-8、4,点P以每秒2个单位的速度运动,点Q以每秒1个单位的速度运动.设点P、Q同时出发,运动时间为t秒.
(1)若点P、Q同时向右运动2秒,则点P表示的数为________,点P、Q之间的距离是________个单位;
(2)经过________秒后,点P、Q重合;
(3)试探究:经过多少秒后,点P、Q两点间的距离为14个单位.
39.已知A、B两点在数轴上表示的数分别为a,b.
(1)对照数轴填写下表:
a
6
-6
-6
-6
b
4
0
4
6
A、B两点的距离
________
________
________
________
(2)若A、B两点间的距离记为d,则d=________(用含a、b的式子表示);
(3)在数轴上到6和-6的距离之和为12的整数点共有________个;
(4)若数轴上点C表示的数为x,当x在________和________之间取值时, |x+1|+|x?2| 的值最小,最小值是________,此时x的整数值为________.
40.阅读下列内容:
数轴上表示数a的点与原点的距离叫做数a的绝对值,记作|a|.数轴上表示数a的点与表示数b的点的距离记作|a﹣b|,如|3﹣5|表示数轴上表示数3的点与表示数5的点的距离,|3+5|=|3﹣(﹣5)|表示数轴上表示数3的点与表示数﹣5的点的距离,|a﹣3|表示数轴上表示数a的点与表示数3的点的距离.
根据以上材料回答下列问题:(将结果直接填写在答题卡相应位置,不写过程)
(1)若|x﹣1|=|x+1|,则x=________,若|x﹣2|=|x+1|,则x=________;
(2)若|x﹣2|+|x+1|=3,则x的取值范围是________;
(3)若|x﹣2|+|x+1|=5,则x的值是________;
(4)若|x﹣2|﹣|x+1|=3,则x能取到的最大值是________.
答案解析部分
一、单选题
1.【答案】 C
解:有一个公共顶点,并且一个角的两边分别是另一个角的两边的反向延长线,具有这种位置关系的两个角,互为对顶角,故A选项不符合题意;
A,B 两点之间的距离就是线段 AB 的长度,故B选项不符合题意;
两点之间,线段最短,故C选项符合题意;
在同一平面内,不相交的两条直线叫做平行线,故D选项不符合题意.
故答案为:C.
2.【答案】 C
解:A、对顶角相等,故该项不符合题意;
B、两点确定一条直线,故该项不符合题意;
C、一个角的补角一定不大于这个角,故该项符合题意;
D、垂线段最短,故该项不符合题意;
故答案为:C.
3.【答案】 A
解:A、在同一平面内,过直线外一点有且只有一条直线与已知直线平行,故本选项说法错误.
B、在同一平面内,过一点有且只有一条直线与已知直线垂直,故本选项说法正确.
C、两点之间的所有连线中,线段最短,故本选项说法正确.
D、对顶角相等故本选项说法正确.
故答案为:A.
4.【答案】 A
解:A、根据题干给出的条件,无法判断∠A=∠B,故此选项符合题意;
B、∵∠ACB=90°,∴∠A+∠B=90°,又∵CD⊥AB,∴∠CDB=90°,∴∠BCD+∠B=90°,∴∠A=∠BCD,故此选项不符合题意;
C、直角三角形中,斜边长大于直角边长,所以AC>AD,故此选项不符合题意;
D、直角三角形中,斜边长大于直角边长,所以BC>CD,故此选项不符合题意.
故答案为:A.
5.【答案】 C
【解析】【解答】∵AC⊥BF,
∴ ∠ACB=90° ,即 ∠ACD+∠1=90° .
故∠1是∠ACD的余角,①正确;
∵CD⊥BE,AC⊥BF,
∴ ∠ADC=∠BDC=90° , ∠ACB=90° ,
∴ ∠ACD+∠DAC=90° , ∠DBC+∠DCB=90° , ∠ACD+∠1=90° , ∠BAC+∠ABC=90° .
故一共有4对互余的角,②错误;
∵ ∠ACD+∠1=90° , ∠DAC+∠ACD=90° ,
∴ ∠1=∠DAC ,
∵ ∠DAC+∠CAE=180° ,
∴ ∠1+∠CAE=180° ,
又∵ ∠1+∠DCF=180° ,
故与 ∠1 互补的角有 ∠CAE 和 ∠DCF ,③错误.
∵AC⊥BF, CD⊥BE,
∴与 ∠ADC 互补的角有: ∠BDC 、 ∠ACB 、 ∠ACF ,④正确.
所以正确的结论为①④.
故答案为:C.
6.【答案】 D
解:A、9:00时时针与分针的夹角是90°,
B、3:30时时针与分针的夹角是90°﹣ 12 ×30°=75°,
C、6:40时时时针与分针的夹角是30°×2﹣30°× 4060 =40°,
D、5:45时时时针与分针的夹角是30°×4﹣30°× 4560 =97.5°,
故答案为:D.
二、填空题
7.【答案】 64.8°
解:由题意可得∠BOD= ∠AOC=25°12′
∵ EO⊥CD
∴∠EOD=90°
∴ ∠BOE=∠EOD?∠BOD=90°?25°12′=64°48′=64.8°.
故答案为:64.8°.
8.【答案】 35
解:∵ OM⊥AB ,
∴∠BOM=90°,
∵ ∠DOM=55° ,
∴∠BOD=90°-55°=35°,
∴∠AOC=∠BOD=35°,
故答案为:35.
9.【答案】 55
解:由题意得
1+2+3+…+10=55个.
故答案为:55.
10.【答案】 m+n 或 ?m+n
解:∵点A到原点的距离为m,点B到原点的距离为n,
∴点A对应的数为±m,点B对应的数为±n,
又∵点B在点A的左边,且m<n,
∴点A对应的数为±m,点B对应的数为﹣n,
∴点A与点B的距离等于m﹣(﹣n)=m+n或﹣m﹣(﹣n)=﹣m+n,
故答案为: m+n 或 ?m+n.
11.【答案】 -5或1
解:设与A点相距3个单位长度的点表示的数为x,则|x+2|=3,解得x=1或x=-5.
故答案为:1或-5.
12.【答案】 9
解:数轴上表示有理数?5.5与3.5两点的距离是3.5?(?5.5)=3.5+5.5=9,
故答案为:9.
13.【答案】 ?7 或3
【解析】【解答】∵点 M(?2,3) 与点 N(x,3) 之间的距离是5
∴ |x+2|=5
化简绝对值得: x+2=5 或 x+2=?5
解得 x=3 或 x=?7
故答案为: ?7 或3.
14.【答案】 51?36' (或 51.6° ).
解:∵ ∠α 与 ∠β 互为余角,
∴ ∠α+∠β=90° ,
∵ ∠α=38°24' ,
∴ ∠β=90°?38°24'=51°36'=51.6° ;
故答案为: 51?36' (或 51.6° ).
15.【答案】 32°
解:∵ OC⊥OA,OD⊥OB .,
∴ ∠AOC=∠BOD=90° ,
∵ ∠AOB+∠COD=∠AOC+∠BOD=90°+90°=180° ,
∴ ∠COD=180°?∠AOB=180°?148°=32° ;
故答案为: 32° .
16.【答案】 58.6°
解:原式=58°+(36÷60)°=58.6°
故答案为58.6°.
17.【答案】 北偏西60°
解:如图:
∵∠ABD=30°,
∴∠CBA=60°,
∴A在B的北偏西60°方向.
18.【答案】 10
【解析】【解答】∵点B在点A北偏东40°方向,点C在点B北偏西 50° 方向
∴∠CBA=90°
故点C到直线AB的距离就是BC的长度
又BC=10m
故答案为:10.
19.【答案】 ②
【解析】【解答】 ①用两根钉子就可以把一根木条固定在墙上,根据两点确定一条直线;
②把弯曲的公路改直,就能够缩短路程,根据两点之间线段最短;
③体育课上,老师测量某个同学的跳远成绩,根据垂线段最短;
故答案为:②.
20.【答案】 22
【解析】【解答】∵∠α=68 ,
∴∠α的余角=90 -68 =22 .
故答案是22 .
21.【答案】 >
解:∠β=25.15°=25°9′,
∵25°15′>25°9′,
∴∠α>∠β,
故答案为:>.
22.【答案】 49.75
【解析】【解答】∵∠α=40°? 15′,
∴∠a的余角=90°-40°? 15′=49°? 45′=49.75°.
故答案为:49.75.
23.【答案】 14°
解:∵∠A=76°,
∴∠A的余角是90°?76°=14°;
故答案为:14°.
24.【答案】 75
解:时针指向3和4的中间,分针指向6,
时针与分针之间的夹角为:
30?÷2+30?×2=15?+60?=75?.
故答案为: 75 .
25.【答案】 50°
【解析】【解答】因为∠A=40°0,
所以∠A的余角=90°-40°=50°.
故答案为:50°.
26.【答案】 150°
解:5时整时,时针与分针所成的角的度数是5×30=150°,
故答案为:150°.
27.【答案】 152
解:∵ ∠α=28° ,∴ ∠α的补角为 180°-∠α=180°-28°=152°.
故答案为:152.
三、计算题
28.【答案】 (1)解:原式= ?314+114?(?2)
=-2+2
=0;
(2)解:原式=-1-8+(-8)+33-32
=-16;
(3)解:原式=168°60′104″-4°19′16″+3°17′42″
=164°41′88″+3°17′42″
=167°58′130″
=168°10″.
29.【答案】 解:(1)原式=﹣4×32﹣(﹣23)×9=﹣6+6=0;
(2)原式=16°51′+115°21′﹣35°29′=131°72′﹣35°29′=96°43′.
四、作图题
30.【答案】 (1)乙;9
(2)解:①如图所示,线段AB,射线AD即为所求;
②如图所示,点M即在射线AD上,又在直线BC上;
③如图所示,点N到A、B、C、D四个点的距离和最短.
解:(1)①甲图的左视图不合题意,乙图符合题意;
故答案为:乙;
②这个几何体最多可由9个小正方体构成,其俯视图如图所示:
故答案为:9;
31.【答案】 解:如图所示:
五、综合题
32.【答案】 (1)450
(2)解:设甲机器人前3分钟的速度为a米/分,
3a=90+3×50,
解得,a=80,
答:机器人前3分钟的速度为80米/分
(3)解:∵前4分钟甲机器人的速度保持不变,在4≤t≤6分钟时,甲的速度变为与乙相同,
∴前4分钟甲机器人的速度为80米/分,在4≤t≤6分钟时,甲的速度为50米/分,
设甲乙相遇前相距28米时出发的时间为b分钟,
80b+28=90+50b,
解得,b= 3115 ,
设甲乙相遇后相距28米时出发的时间为c分钟,
80c﹣28=90+50c,
解得,c= 5915 ,
答:两机器人前6分钟内出发 3115 分或 5915 分时相距28米
(4)解:∵6分钟后甲机器人的速度又恢复为原来出发时的速度,
∴6分钟后甲机器人的速度是80米/分,
当t=6时,甲乙两机器人的距离为:[80×4+50×(6﹣2)]﹣(90+50×6)=60(米),
当甲到达终点C时,t={(90+450)﹣[80×4+50×(6﹣2)]}÷80+6=7.5(分),
当乙到达终点C时,t=450÷50=9(分),
∴当6<t≤7.5时,S=60+(80﹣50)×(t﹣6)=30t﹣120,
当7.5<t≤9时,S=450﹣50×7.5﹣50(t﹣7.5)=﹣50t+450,
由上可得,当t>6时,甲、乙两机器人之间的距离S= {30t-120(6解:(1)由题意可得,
B、C两点之间的距离是:50×9=450(米),
故答案为450;
33.【答案】 (1)5
(2)|x-7|
(3)?8;?3或?13
(4)解:如图,
|x+2018|+|x+504|+|x?2017|的最小值,即|2017?(?2018)|=4035
解:(1)|3?(?2)|=5;
故答案为:5;
( 2 )数轴上有理数x与有理数7所对应两点之间的距离用绝对值符号可以表示为|x?7|
故答案为:|x?7|;
?( 3 )代数式|x+8|可以表示数轴上有理数x与有理数?8所对应的两点之间的距离;若|x+8|=5,则x=?3或?13,
故答案为:?8,?3或?13;
34.【答案】 (1)解:设x秒后甲与乙相遇,则:
4x+6x=34 ,
解得 x=3.4 ,
4×3.4=13.6 ,
?24+13.6=?10.4 .
故甲、乙 3.4 秒后相遇;
(2)解:设y秒后甲到A,B,C三点的距离之和为40个单位,
B点距A,C两点的距离为14+20=34<40,A点距B、C两点的距离为14+34=48>40,C点距A、B的距离为34+20=54>40,故甲应位于AB或BC之间.
①甲位于AB之间时:
4y+[?10?(?24)?4y]+[?10?(?24)?4y+10?(?10)]=40 ,
解得 y=2 ;
②甲位于BC之间时:
4y+{4y?[?10?(?24)]}+[10?(?24)?4y]=40 ,
解得 y=5 ,
故甲出发 2 秒或 5 秒后,甲到A、B、C三点的距离和为40个单位;
(3)-44
解:(3)①甲从A向右运动2秒时返回,设m秒后与乙相遇,此时甲、乙表示在数轴上为同一点,所表示的数相同.
甲表示的数为: ?24+4×2?4m ;乙表示的数为: 10?6×2?6m ,
依据题意得: ?24+4×2?4m=10?6×2?6m ,
解得: m=7 ,
相遇点表示的数为: ?24+4×2?4m=?44 ,
②甲从A向右运动5秒时返回,设n秒后与乙相遇.
甲表示的数为: ?24+4×5?4n ;乙表示的数为: 10?6×5?6n ,
依据题意得: ?24+4×5?4n=10?6×5?6n ,
解得: n=?8 (不合题意舍去),
即甲从A向右运动2秒时返回,能在数轴上与乙相遇,相遇点表示的数为-44.
故答案为:-44.
35.【答案】 (1)10;18
(2)解:答:不变.
∵经过t秒后,A、B、C三点所对应的数分别是18+t,8﹣2t,﹣10﹣5t,
∴BC=(8﹣2t)﹣(﹣10﹣5t)= 3t+18,?? AB=(18+t)﹣(8﹣2t)=3t+10,
∴BC﹣AB=(3t+18)﹣(3t+10)=8.
∴BC﹣AB的值不会随着时间t的变化而改变
(3)解:①当0<t≤10时,点Q还在点A处,P、Q两点所对应的数分别是18﹣t,18? ∴PQ═t,
②当t>10时,P、Q两点所对应的数分别是18﹣t,18﹣3(t﹣10)
由18﹣3(t﹣10)﹣(18﹣t)=0? 解得t=15
当10<t≤15时,点Q在点P的右边,? ∴PQ=[18﹣3(t﹣10)]﹣(18﹣t)=30﹣2t,
当15<t≤28时,点P在点Q的右边,? ∴PQ=18﹣t﹣[18﹣3(t﹣10)]=2t-30.
解:(1)AB=18-8=10,BC=8-(-10)=18;
故答案为:10,18;
36.【答案】 (1)3;7
(2)-4或2
(3)解:∵点A表示的数是-1,点B表示的数是3,
∴|AB|=4
∴ |AC| = 2,
∴点C表示的数为1或-3.
解:(1)数轴上表示2和5两点之间的距离是3,数轴上表示-3和4两点之间的距离是7,
故答案为:3;7;
(2)∵数轴上点B表示的数是-1,|AB| = 3,
∴点B表示的数是-4或2
故答案为:-4或2;
37.【答案】 (1)2
(2)-2;解:∵A、B两点之间的距离为11经折叠后重合, ∴A、B距离对称点的距离为11÷2=5.5, 又∵两数关于与2表示的点对折,且A在B的左侧 ∴点B表示的数为2+5.5=7.5,点A表示的数为2-5.5=-3.5.5
解:(1)∵1表示的点与-1表示的点重合,
∴两数关于原点对折,
∴ ?2 表示的点与数2表示的点重合.
故答案为:2;
(2)①∵-1表示的点与5表示的点重合,
∴两数关于与2表示的点对折,
∴6表示的点与数-2表示的点重合.
故答案为:-2;
38.【答案】 (1)-4;10
(2)4,12
(3)解:P向左运动,Q向右运动时:①2t+t+12=14 解得 t= 23 .
点P、Q同时向左运动②2t=26+t,解得t=26
点P、Q同时向右运动?? ③2t+12=14+,解得t=2.
点P向右运动,Q向左运动时:④2t+t=12+14,解得t= 263
答:经过 23 、26、2、 263 秒时,P、Q相距14个单位.
解:(1)P表示的数:-8+2×2=-4,
Q表示的数:4+1×2=6
所以点P、Q之间的距离是6-(-4)= 10;
故答案为:-4,10;
(2)设经t秒点P、Q重合相遇时:
2t+t=12? 解得t=4;
追及时:2t-t=12? 解得t=12;
故答案为:4,12;
39.【答案】 (1)2;6;10;12
(2)|a-b|或|b-a|
(3)13
(4)-1;2;3;-1,0,1,2
解:(1)对照数轴可得
当a=6,b=4时,A、B两点的距离:|6-4|=2;
当a=-6,b=0时,A、B两点的距离:|-6-0|=6;
当a=-6,b=4时,A、B两点的距离:|-6-4|=10;
当a=-6,b=6时,A、B两点的距离:|-6-6|=12;
故可填写表:
a
6
-6
-6
-6
b
4
0
4
6
A、B两点的距离
2
6
10
12
( 2 )由(1)可得:d=|a﹣b|或d=|b﹣a|;
( 3 )结合数轴可得,当整数点对应的数小于-6时,在数轴上到6和-6的距离之和大于12;当整数点对应的数大于6时,在数轴上到6和-6的距离之和大于12;
当整数点对应的数在﹣6和6之间时,所有整数均满足到6和﹣6的距离之和为12,有:﹣6、﹣5、﹣4、﹣3、﹣2、﹣1、0、1、2、3、4、5、6共13个;
故答案为:13;
( 4 )根据数轴的几何意义可得﹣1和2之间的任何一点均能使|x+1|+|x﹣2|取得的值最小.故可得:点C的范围在:﹣1≤x≤2时,能满足题意.最小值是2-(-1)=3,此时x的整数值为-1,0,1,2.
故答案为:-1;2;3;-1,0,1,2.
40.【答案】 (1)0;12
(2)-1≤x≤2
(3)-2或3
(4)-1
解:(1)|x-1|=|x+1|表示数轴上表示x的点到表示1和-1的距离相等,因此到1和-1距离相等的点表示的数为 1+(?1)2=0 ,
|x-2|=|x+1|表示数轴上表示x的点到表示2和-1的距离相等,因此到2和-1距离相等的点表示的数为 2+(?1)2=12 ,
故答案为:0, 12 ;(2)|x-2|+|x+1|=3表示的意义是数轴上表示x的点到表示2和-1两点的距离之和为3,
∵2和-1两点的距离之和为3
∴表示x的点在2和-1之间
∴-1≤x≤2,(3)|x﹣2|+|x+1|=5表示的意义是数轴上表示数x的点与表示数2的点距离比它到表示-1的点的距离等于5,
∵2和-1两点的距离之和为3
∴在2的右边多出(5-3)÷2=1,即表示数x=2+1=3;
或者在-1的左边多出(5-3)÷2=1,即表示数x=-1-1=-2;
故答案为-2或3;(4)|x-2|-|x+1|=3表示的意义是数轴上表示数x的点与表示数2的点距离比它到表示-1的点的距离大3,根据数轴直观可得,
x≤-1,x的最大值为-1,
故答案为:-1;.
一、单选题
1.下列说法正确的是( ??)
A.?具有公共顶点的两个角是对顶角
B.?A,B 两点之间的距离就是线段 AB
C.?两点之间,线段最短
D.?不相交的两条直线叫做平行线
2.下列说法不正确的是(?? )
A.?对顶角相等??????????B.?两点确定一条直线??????????C.?一个角的补角一定大于这个角??????????D.?垂线段最短
3.下列说法错误的是(?? )
A.?平面内过一点有且只有一条直线与已知直线平行
B.?平面内过一点有且只有一条直线与已知直线垂直
C.?两点之间的所有连线中,线段最短
D.?对顶角相等
4.如图,∠ACB=90°,CD⊥AB,D为垂足.下列判断错误的是(?? )
A.?∠A=∠B????????????????????????????B.?∠A=∠BCD ??C.?AC>AD????????????????????????????D.?BC>CD
5.如图,已知点A是射线BE上一点,过A作AC⊥BF,垂足为C,CD⊥BE,垂足为D.给出下列结论:①∠1是∠ACD的余角;②图中互余的角共有3对;③∠1的补角只有∠DCF;④与∠ADC互补的角共有3个.其中正确结论有(? )
A.?①????????????????????????????????????B.?①②③????????????????????????????????????C.?①④????????????????????????????????????D.?②③④
6.下列时刻中,时针与分针所成的角(小于平角)最大的是(?? )
A.?9:00?????????????????????????????????B.?3:30?????????????????????????????????C.?6:40?????????????????????????????????D.?5:45
二、填空题
7.已知直线 AB 与直线 CD 相交于点 O , EO⊥CD ,垂足为 O .若 ∠AOC=25°12′ ,则 ∠BOE 的度数为________.(单位用度表示)
8.如图,直线AB与CD相交于点O , OM⊥AB ,若 ∠DOM=55° ,则 ∠AOC =________°.
9.G101是一班从北京南站开往上海虹桥的下行(单向)高速列车,停靠如图所示的11个站点,则该趟列车共有________个乘车区间(指旅客乘车地与目的地之间的区间).
10.数轴上有点A和点B,点A到原点的距离为m,点B到原点的距离为n,且点B在点A的左边,若m<n,则点A与点B的距离等于________.
11.数轴上A点表示的数为-2,则A点相距3个单位长度的点表示的数是________
12.数轴上表示有理数﹣5.5与3.5两点的距离是________.
13.在平面直角坐标系中,若点M(﹣2,3)与点N(x,3)之间的距离是5,则x的值是________.
14.已知 ∠α 与 ∠β 互为余角, ∠α=38?24' ,则 ∠β= ________.
15.如图,已知 OC⊥OA,OD⊥OB .若 ∠AOB=148° ,则 ∠COD= ________.
16.58°36′=________°.
17.如图,A在B的________方向.
18.如图,点B在点A北偏东40°方向,点C在点B北偏西50° 方向,? BC=10m,则点 C到直线 AB的距离为________ m.
19.下列三个日常现象:
①用两根钉子就可以把一根木条固定在墙上;②把弯曲的公路改直,就能够缩短路程;③体育课上,老师测量某名同学的跳远成绩.其中,可以用“两点之间线段最短”来解释的是________ .(填序号)
20.若∠α=68 ,则∠α的余角为________ .
21.已知∠α=25°15′,∠β=25.15°,则∠α________∠β(填“>”,“<”或“=”).
22.若∠α=40°? 15′,则∠α的余角等于________°.
23.已知 ∠A=76° ,则 ∠A 的余角的度数是________.
24.下午3点30分时,钟面上时针与分针所成的角等于________°.
25.已知∠A=40°,则∠A的余角等于________.
26.北京时间上午5点整,时针与分针所成的角的度数是________.
27.已知∠α=28°,则∠α的补角为________°.
三、计算题
28.???
(1)?314?(?114)?(?223+23)
(2)?12?|?8|+(?2)3+(118?43)×24
(3)42°15′26″×4?21°36′20″÷5+3.295°
29.计算:
(1)﹣22÷23﹣(﹣23)×(﹣3)2
(2)16°51′+38°27′×3﹣35°29′.
四、作图题
30.画图,探究:
(1)一个正方体组合图形的主视图、左视图(如图1)所示.
①这个几何体可能是(图2)甲、乙中的________;
②这个几何体最多可由________个小正方体构成,请在图3中画出符合最多情况的一个俯视图.
(2)如图,已知一平面内的四个点A、B、C、D,根据要求用直尺画图.
①画线段AB,射线AD;
②找一点M,使M点即在射线AD上,又在直线BC上;
③找一点N,使N到A、B、C、D四个点的距离和最短.
31.如图,已知直线l和直线外三点A,B,C,按下列要求画图:
①画射线CB交直线l于点F;
②连接BA;
③在直线l上确定点E,使得AE+CE最小.
五、综合题
32.有一科技小组进行了机器人行走性能试验,在试验场地有A、B、C三点顺次在同一笔直的赛道上,A、B两点之间的距离是90米,甲、乙两机器人分别从A、B两点同时同向出发到终点C,乙机器人始终以50米分的速度行走,乙行走9分钟到达C点.设两机器人出发时间为t(分钟),当t=3分钟时,甲追上乙.
请解答下面问题:
(1)B、C两点之间的距离是________米.
(2)求甲机器人前3分钟的速度为多少米/分?
(3)若前4分钟甲机器人的速度保持不变,在4≤t≤6分钟时,甲的速度变为与乙相同,求两机器人前6分钟内出发多长时间相距28米?
(4)若6分钟后甲机器人的速度又恢复为原来出发时的速度,直接写出当t>6时,甲、乙两机器人之间的距离S.(用含t的代数式表示).
33.阅读下面材料:如图,点A、B在数轴上分别表示有理数a、b,则A、B两点之间的距离可以表示为|a?b|.
根据阅读材料与你的理解回答下列问题:
(1)数轴上表示3与?2的两点之间的距离是________.
(2)数轴上有理数x与有理数7所对应两点之间的距离用绝对值符号可以表示为________.
(3)代数式|x+8|可以表示数轴上有理数x与有理数________?所对应的两点之间的距离;若|x+8|=5,则x=________.
(4)求代数式|x+2018|+|x+504|+|x?2017|的最小值.
34.已知数轴上有A、B、C三点,分别代表-24,-10,10,两只电子蚂蚁甲、乙分别从A、C两点同时相向而行,甲的速度为4个单位/秒,乙的速度为6个单位/秒.
(1)甲、乙多少秒后相遇?
(2)甲出发多少秒后,甲到A、B、C三点的距离和为40个单位?
(3)当甲到A、B、C三点的距离和为40个单位时,甲调头返回,当甲、乙在数轴上再次相遇时,相遇点表示的数是________.
35.如图,已知数轴上有A、B、C三个点,它们表示的数分别是18,8,﹣10.
(1)填空:AB=________,BC=________;
(2)若点A以每秒1个单位长度的速度向右运动,同时,点B和点C分别以每秒2个单位长度和5个单位长度的速度向左运动.试探索:BC﹣AB的值是否随着时间t的变化而改变?请说明理由.
(3)现有动点P、Q都从A点出发,点P以每秒1个单位长度的速度向终点C移动;当点P移动到B点时,点Q才从A点出发,并以每秒3个单位长度的速度向左移动,且当点P到达C点时,点Q就停止移动.设点P移动的时间为t秒,试用含t的代数式表示P、Q两点间的距离.
36.阅读下面材料:
若点A、B在数轴上分别表示数a,b,则A、B两点之间的距离表示为|AB|
(1)数轴上表示2和5两点之间的距离是________,数轴上表示-3和4两点之间的距离是________.
(2)若数轴上点B表示的数是-1,且|AB| = 3,则a=________.
(3)在数轴上有三个点A, B, C若点A表示的数是-1,点B表示的数是3,且|AB| + |AC| = 6 ,求点C表示的数.
37.已知在纸面上有一数轴 ( 如图 ) ,折叠纸面:
(1)若1表示的点与-1表示的点重合,则 ?2 表示的点与数________表示的点重合;
(2)若-1表示的点与5表示的点重合,回答以下问题:
①6表示的点与数________表示的点重合;
②若数轴上A、B两点之间的距离为 11(A 在B的左侧 ) ,且A、B两点经折叠后重合,求A、B两点表示的数是多少?________
38.如图,点P、Q在数轴上表示的数分别是-8、4,点P以每秒2个单位的速度运动,点Q以每秒1个单位的速度运动.设点P、Q同时出发,运动时间为t秒.
(1)若点P、Q同时向右运动2秒,则点P表示的数为________,点P、Q之间的距离是________个单位;
(2)经过________秒后,点P、Q重合;
(3)试探究:经过多少秒后,点P、Q两点间的距离为14个单位.
39.已知A、B两点在数轴上表示的数分别为a,b.
(1)对照数轴填写下表:
a
6
-6
-6
-6
b
4
0
4
6
A、B两点的距离
________
________
________
________
(2)若A、B两点间的距离记为d,则d=________(用含a、b的式子表示);
(3)在数轴上到6和-6的距离之和为12的整数点共有________个;
(4)若数轴上点C表示的数为x,当x在________和________之间取值时, |x+1|+|x?2| 的值最小,最小值是________,此时x的整数值为________.
40.阅读下列内容:
数轴上表示数a的点与原点的距离叫做数a的绝对值,记作|a|.数轴上表示数a的点与表示数b的点的距离记作|a﹣b|,如|3﹣5|表示数轴上表示数3的点与表示数5的点的距离,|3+5|=|3﹣(﹣5)|表示数轴上表示数3的点与表示数﹣5的点的距离,|a﹣3|表示数轴上表示数a的点与表示数3的点的距离.
根据以上材料回答下列问题:(将结果直接填写在答题卡相应位置,不写过程)
(1)若|x﹣1|=|x+1|,则x=________,若|x﹣2|=|x+1|,则x=________;
(2)若|x﹣2|+|x+1|=3,则x的取值范围是________;
(3)若|x﹣2|+|x+1|=5,则x的值是________;
(4)若|x﹣2|﹣|x+1|=3,则x能取到的最大值是________.
答案解析部分
一、单选题
1.【答案】 C
解:有一个公共顶点,并且一个角的两边分别是另一个角的两边的反向延长线,具有这种位置关系的两个角,互为对顶角,故A选项不符合题意;
A,B 两点之间的距离就是线段 AB 的长度,故B选项不符合题意;
两点之间,线段最短,故C选项符合题意;
在同一平面内,不相交的两条直线叫做平行线,故D选项不符合题意.
故答案为:C.
2.【答案】 C
解:A、对顶角相等,故该项不符合题意;
B、两点确定一条直线,故该项不符合题意;
C、一个角的补角一定不大于这个角,故该项符合题意;
D、垂线段最短,故该项不符合题意;
故答案为:C.
3.【答案】 A
解:A、在同一平面内,过直线外一点有且只有一条直线与已知直线平行,故本选项说法错误.
B、在同一平面内,过一点有且只有一条直线与已知直线垂直,故本选项说法正确.
C、两点之间的所有连线中,线段最短,故本选项说法正确.
D、对顶角相等故本选项说法正确.
故答案为:A.
4.【答案】 A
解:A、根据题干给出的条件,无法判断∠A=∠B,故此选项符合题意;
B、∵∠ACB=90°,∴∠A+∠B=90°,又∵CD⊥AB,∴∠CDB=90°,∴∠BCD+∠B=90°,∴∠A=∠BCD,故此选项不符合题意;
C、直角三角形中,斜边长大于直角边长,所以AC>AD,故此选项不符合题意;
D、直角三角形中,斜边长大于直角边长,所以BC>CD,故此选项不符合题意.
故答案为:A.
5.【答案】 C
【解析】【解答】∵AC⊥BF,
∴ ∠ACB=90° ,即 ∠ACD+∠1=90° .
故∠1是∠ACD的余角,①正确;
∵CD⊥BE,AC⊥BF,
∴ ∠ADC=∠BDC=90° , ∠ACB=90° ,
∴ ∠ACD+∠DAC=90° , ∠DBC+∠DCB=90° , ∠ACD+∠1=90° , ∠BAC+∠ABC=90° .
故一共有4对互余的角,②错误;
∵ ∠ACD+∠1=90° , ∠DAC+∠ACD=90° ,
∴ ∠1=∠DAC ,
∵ ∠DAC+∠CAE=180° ,
∴ ∠1+∠CAE=180° ,
又∵ ∠1+∠DCF=180° ,
故与 ∠1 互补的角有 ∠CAE 和 ∠DCF ,③错误.
∵AC⊥BF, CD⊥BE,
∴与 ∠ADC 互补的角有: ∠BDC 、 ∠ACB 、 ∠ACF ,④正确.
所以正确的结论为①④.
故答案为:C.
6.【答案】 D
解:A、9:00时时针与分针的夹角是90°,
B、3:30时时针与分针的夹角是90°﹣ 12 ×30°=75°,
C、6:40时时时针与分针的夹角是30°×2﹣30°× 4060 =40°,
D、5:45时时时针与分针的夹角是30°×4﹣30°× 4560 =97.5°,
故答案为:D.
二、填空题
7.【答案】 64.8°
解:由题意可得∠BOD= ∠AOC=25°12′
∵ EO⊥CD
∴∠EOD=90°
∴ ∠BOE=∠EOD?∠BOD=90°?25°12′=64°48′=64.8°.
故答案为:64.8°.
8.【答案】 35
解:∵ OM⊥AB ,
∴∠BOM=90°,
∵ ∠DOM=55° ,
∴∠BOD=90°-55°=35°,
∴∠AOC=∠BOD=35°,
故答案为:35.
9.【答案】 55
解:由题意得
1+2+3+…+10=55个.
故答案为:55.
10.【答案】 m+n 或 ?m+n
解:∵点A到原点的距离为m,点B到原点的距离为n,
∴点A对应的数为±m,点B对应的数为±n,
又∵点B在点A的左边,且m<n,
∴点A对应的数为±m,点B对应的数为﹣n,
∴点A与点B的距离等于m﹣(﹣n)=m+n或﹣m﹣(﹣n)=﹣m+n,
故答案为: m+n 或 ?m+n.
11.【答案】 -5或1
解:设与A点相距3个单位长度的点表示的数为x,则|x+2|=3,解得x=1或x=-5.
故答案为:1或-5.
12.【答案】 9
解:数轴上表示有理数?5.5与3.5两点的距离是3.5?(?5.5)=3.5+5.5=9,
故答案为:9.
13.【答案】 ?7 或3
【解析】【解答】∵点 M(?2,3) 与点 N(x,3) 之间的距离是5
∴ |x+2|=5
化简绝对值得: x+2=5 或 x+2=?5
解得 x=3 或 x=?7
故答案为: ?7 或3.
14.【答案】 51?36' (或 51.6° ).
解:∵ ∠α 与 ∠β 互为余角,
∴ ∠α+∠β=90° ,
∵ ∠α=38°24' ,
∴ ∠β=90°?38°24'=51°36'=51.6° ;
故答案为: 51?36' (或 51.6° ).
15.【答案】 32°
解:∵ OC⊥OA,OD⊥OB .,
∴ ∠AOC=∠BOD=90° ,
∵ ∠AOB+∠COD=∠AOC+∠BOD=90°+90°=180° ,
∴ ∠COD=180°?∠AOB=180°?148°=32° ;
故答案为: 32° .
16.【答案】 58.6°
解:原式=58°+(36÷60)°=58.6°
故答案为58.6°.
17.【答案】 北偏西60°
解:如图:
∵∠ABD=30°,
∴∠CBA=60°,
∴A在B的北偏西60°方向.
18.【答案】 10
【解析】【解答】∵点B在点A北偏东40°方向,点C在点B北偏西 50° 方向
∴∠CBA=90°
故点C到直线AB的距离就是BC的长度
又BC=10m
故答案为:10.
19.【答案】 ②
【解析】【解答】 ①用两根钉子就可以把一根木条固定在墙上,根据两点确定一条直线;
②把弯曲的公路改直,就能够缩短路程,根据两点之间线段最短;
③体育课上,老师测量某个同学的跳远成绩,根据垂线段最短;
故答案为:②.
20.【答案】 22
【解析】【解答】∵∠α=68 ,
∴∠α的余角=90 -68 =22 .
故答案是22 .
21.【答案】 >
解:∠β=25.15°=25°9′,
∵25°15′>25°9′,
∴∠α>∠β,
故答案为:>.
22.【答案】 49.75
【解析】【解答】∵∠α=40°? 15′,
∴∠a的余角=90°-40°? 15′=49°? 45′=49.75°.
故答案为:49.75.
23.【答案】 14°
解:∵∠A=76°,
∴∠A的余角是90°?76°=14°;
故答案为:14°.
24.【答案】 75
解:时针指向3和4的中间,分针指向6,
时针与分针之间的夹角为:
30?÷2+30?×2=15?+60?=75?.
故答案为: 75 .
25.【答案】 50°
【解析】【解答】因为∠A=40°0,
所以∠A的余角=90°-40°=50°.
故答案为:50°.
26.【答案】 150°
解:5时整时,时针与分针所成的角的度数是5×30=150°,
故答案为:150°.
27.【答案】 152
解:∵ ∠α=28° ,∴ ∠α的补角为 180°-∠α=180°-28°=152°.
故答案为:152.
三、计算题
28.【答案】 (1)解:原式= ?314+114?(?2)
=-2+2
=0;
(2)解:原式=-1-8+(-8)+33-32
=-16;
(3)解:原式=168°60′104″-4°19′16″+3°17′42″
=164°41′88″+3°17′42″
=167°58′130″
=168°10″.
29.【答案】 解:(1)原式=﹣4×32﹣(﹣23)×9=﹣6+6=0;
(2)原式=16°51′+115°21′﹣35°29′=131°72′﹣35°29′=96°43′.
四、作图题
30.【答案】 (1)乙;9
(2)解:①如图所示,线段AB,射线AD即为所求;
②如图所示,点M即在射线AD上,又在直线BC上;
③如图所示,点N到A、B、C、D四个点的距离和最短.
解:(1)①甲图的左视图不合题意,乙图符合题意;
故答案为:乙;
②这个几何体最多可由9个小正方体构成,其俯视图如图所示:
故答案为:9;
31.【答案】 解:如图所示:
五、综合题
32.【答案】 (1)450
(2)解:设甲机器人前3分钟的速度为a米/分,
3a=90+3×50,
解得,a=80,
答:机器人前3分钟的速度为80米/分
(3)解:∵前4分钟甲机器人的速度保持不变,在4≤t≤6分钟时,甲的速度变为与乙相同,
∴前4分钟甲机器人的速度为80米/分,在4≤t≤6分钟时,甲的速度为50米/分,
设甲乙相遇前相距28米时出发的时间为b分钟,
80b+28=90+50b,
解得,b= 3115 ,
设甲乙相遇后相距28米时出发的时间为c分钟,
80c﹣28=90+50c,
解得,c= 5915 ,
答:两机器人前6分钟内出发 3115 分或 5915 分时相距28米
(4)解:∵6分钟后甲机器人的速度又恢复为原来出发时的速度,
∴6分钟后甲机器人的速度是80米/分,
当t=6时,甲乙两机器人的距离为:[80×4+50×(6﹣2)]﹣(90+50×6)=60(米),
当甲到达终点C时,t={(90+450)﹣[80×4+50×(6﹣2)]}÷80+6=7.5(分),
当乙到达终点C时,t=450÷50=9(分),
∴当6<t≤7.5时,S=60+(80﹣50)×(t﹣6)=30t﹣120,
当7.5<t≤9时,S=450﹣50×7.5﹣50(t﹣7.5)=﹣50t+450,
由上可得,当t>6时,甲、乙两机器人之间的距离S= {30t-120(6
B、C两点之间的距离是:50×9=450(米),
故答案为450;
33.【答案】 (1)5
(2)|x-7|
(3)?8;?3或?13
(4)解:如图,
|x+2018|+|x+504|+|x?2017|的最小值,即|2017?(?2018)|=4035
解:(1)|3?(?2)|=5;
故答案为:5;
( 2 )数轴上有理数x与有理数7所对应两点之间的距离用绝对值符号可以表示为|x?7|
故答案为:|x?7|;
?( 3 )代数式|x+8|可以表示数轴上有理数x与有理数?8所对应的两点之间的距离;若|x+8|=5,则x=?3或?13,
故答案为:?8,?3或?13;
34.【答案】 (1)解:设x秒后甲与乙相遇,则:
4x+6x=34 ,
解得 x=3.4 ,
4×3.4=13.6 ,
?24+13.6=?10.4 .
故甲、乙 3.4 秒后相遇;
(2)解:设y秒后甲到A,B,C三点的距离之和为40个单位,
B点距A,C两点的距离为14+20=34<40,A点距B、C两点的距离为14+34=48>40,C点距A、B的距离为34+20=54>40,故甲应位于AB或BC之间.
①甲位于AB之间时:
4y+[?10?(?24)?4y]+[?10?(?24)?4y+10?(?10)]=40 ,
解得 y=2 ;
②甲位于BC之间时:
4y+{4y?[?10?(?24)]}+[10?(?24)?4y]=40 ,
解得 y=5 ,
故甲出发 2 秒或 5 秒后,甲到A、B、C三点的距离和为40个单位;
(3)-44
解:(3)①甲从A向右运动2秒时返回,设m秒后与乙相遇,此时甲、乙表示在数轴上为同一点,所表示的数相同.
甲表示的数为: ?24+4×2?4m ;乙表示的数为: 10?6×2?6m ,
依据题意得: ?24+4×2?4m=10?6×2?6m ,
解得: m=7 ,
相遇点表示的数为: ?24+4×2?4m=?44 ,
②甲从A向右运动5秒时返回,设n秒后与乙相遇.
甲表示的数为: ?24+4×5?4n ;乙表示的数为: 10?6×5?6n ,
依据题意得: ?24+4×5?4n=10?6×5?6n ,
解得: n=?8 (不合题意舍去),
即甲从A向右运动2秒时返回,能在数轴上与乙相遇,相遇点表示的数为-44.
故答案为:-44.
35.【答案】 (1)10;18
(2)解:答:不变.
∵经过t秒后,A、B、C三点所对应的数分别是18+t,8﹣2t,﹣10﹣5t,
∴BC=(8﹣2t)﹣(﹣10﹣5t)= 3t+18,?? AB=(18+t)﹣(8﹣2t)=3t+10,
∴BC﹣AB=(3t+18)﹣(3t+10)=8.
∴BC﹣AB的值不会随着时间t的变化而改变
(3)解:①当0<t≤10时,点Q还在点A处,P、Q两点所对应的数分别是18﹣t,18? ∴PQ═t,
②当t>10时,P、Q两点所对应的数分别是18﹣t,18﹣3(t﹣10)
由18﹣3(t﹣10)﹣(18﹣t)=0? 解得t=15
当10<t≤15时,点Q在点P的右边,? ∴PQ=[18﹣3(t﹣10)]﹣(18﹣t)=30﹣2t,
当15<t≤28时,点P在点Q的右边,? ∴PQ=18﹣t﹣[18﹣3(t﹣10)]=2t-30.
解:(1)AB=18-8=10,BC=8-(-10)=18;
故答案为:10,18;
36.【答案】 (1)3;7
(2)-4或2
(3)解:∵点A表示的数是-1,点B表示的数是3,
∴|AB|=4
∴ |AC| = 2,
∴点C表示的数为1或-3.
解:(1)数轴上表示2和5两点之间的距离是3,数轴上表示-3和4两点之间的距离是7,
故答案为:3;7;
(2)∵数轴上点B表示的数是-1,|AB| = 3,
∴点B表示的数是-4或2
故答案为:-4或2;
37.【答案】 (1)2
(2)-2;解:∵A、B两点之间的距离为11经折叠后重合, ∴A、B距离对称点的距离为11÷2=5.5, 又∵两数关于与2表示的点对折,且A在B的左侧 ∴点B表示的数为2+5.5=7.5,点A表示的数为2-5.5=-3.5.5
解:(1)∵1表示的点与-1表示的点重合,
∴两数关于原点对折,
∴ ?2 表示的点与数2表示的点重合.
故答案为:2;
(2)①∵-1表示的点与5表示的点重合,
∴两数关于与2表示的点对折,
∴6表示的点与数-2表示的点重合.
故答案为:-2;
38.【答案】 (1)-4;10
(2)4,12
(3)解:P向左运动,Q向右运动时:①2t+t+12=14 解得 t= 23 .
点P、Q同时向左运动②2t=26+t,解得t=26
点P、Q同时向右运动?? ③2t+12=14+,解得t=2.
点P向右运动,Q向左运动时:④2t+t=12+14,解得t= 263
答:经过 23 、26、2、 263 秒时,P、Q相距14个单位.
解:(1)P表示的数:-8+2×2=-4,
Q表示的数:4+1×2=6
所以点P、Q之间的距离是6-(-4)= 10;
故答案为:-4,10;
(2)设经t秒点P、Q重合相遇时:
2t+t=12? 解得t=4;
追及时:2t-t=12? 解得t=12;
故答案为:4,12;
39.【答案】 (1)2;6;10;12
(2)|a-b|或|b-a|
(3)13
(4)-1;2;3;-1,0,1,2
解:(1)对照数轴可得
当a=6,b=4时,A、B两点的距离:|6-4|=2;
当a=-6,b=0时,A、B两点的距离:|-6-0|=6;
当a=-6,b=4时,A、B两点的距离:|-6-4|=10;
当a=-6,b=6时,A、B两点的距离:|-6-6|=12;
故可填写表:
a
6
-6
-6
-6
b
4
0
4
6
A、B两点的距离
2
6
10
12
( 2 )由(1)可得:d=|a﹣b|或d=|b﹣a|;
( 3 )结合数轴可得,当整数点对应的数小于-6时,在数轴上到6和-6的距离之和大于12;当整数点对应的数大于6时,在数轴上到6和-6的距离之和大于12;
当整数点对应的数在﹣6和6之间时,所有整数均满足到6和﹣6的距离之和为12,有:﹣6、﹣5、﹣4、﹣3、﹣2、﹣1、0、1、2、3、4、5、6共13个;
故答案为:13;
( 4 )根据数轴的几何意义可得﹣1和2之间的任何一点均能使|x+1|+|x﹣2|取得的值最小.故可得:点C的范围在:﹣1≤x≤2时,能满足题意.最小值是2-(-1)=3,此时x的整数值为-1,0,1,2.
故答案为:-1;2;3;-1,0,1,2.
40.【答案】 (1)0;12
(2)-1≤x≤2
(3)-2或3
(4)-1
解:(1)|x-1|=|x+1|表示数轴上表示x的点到表示1和-1的距离相等,因此到1和-1距离相等的点表示的数为 1+(?1)2=0 ,
|x-2|=|x+1|表示数轴上表示x的点到表示2和-1的距离相等,因此到2和-1距离相等的点表示的数为 2+(?1)2=12 ,
故答案为:0, 12 ;(2)|x-2|+|x+1|=3表示的意义是数轴上表示x的点到表示2和-1两点的距离之和为3,
∵2和-1两点的距离之和为3
∴表示x的点在2和-1之间
∴-1≤x≤2,(3)|x﹣2|+|x+1|=5表示的意义是数轴上表示数x的点与表示数2的点距离比它到表示-1的点的距离等于5,
∵2和-1两点的距离之和为3
∴在2的右边多出(5-3)÷2=1,即表示数x=2+1=3;
或者在-1的左边多出(5-3)÷2=1,即表示数x=-1-1=-2;
故答案为-2或3;(4)|x-2|-|x+1|=3表示的意义是数轴上表示数x的点与表示数2的点距离比它到表示-1的点的距离大3,根据数轴直观可得,
x≤-1,x的最大值为-1,
故答案为:-1;.
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
