2.1-2.5 直线与圆的位置关系同步测试卷(含解析)
文档属性
| 名称 | 2.1-2.5 直线与圆的位置关系同步测试卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 439.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-31 17:01:57 | ||
图片预览




文档简介
初中数学苏科版九年级上册2.1-2.5 同步测试卷
一、单选题
1.如图,点 A , B , C 在 ⊙O 上, BC//OA , ∠A=20° ,则 ∠B 的度数为(?? )
A.?10°????????????????????????????????????B.?20°????????????????????????????????????C.?40°????????????????????????????????????D.?50°
2.如图,在正八边形ABCDEFGH中,连接AC,AE,则AEAC的值是( )
A.?1?????????????????????????????????????????B.?2?????????????????????????????????????????C.?2?????????????????????????????????????????D.?3?
3.如图,△ABC内接于⊙O,∠OBC=40°,则∠A的度数为( ??)
A.?80°?????????????????????????????????????B.?100°?????????????????????????????????????C.?110°?????????????????????????????????????D.?130°
4.如图, ⊙C 的圆心 C 的坐标为 (1,1) ,半径为1,直线 l 的表达式为 y=?2x+6 , P 是直线 l 上的动点, Q 是 ⊙C 上的动点,则 PQ 的最小值是(?? )
A.?355?1????????????????????????????????B.?655?1????????????????????????????????C.?355????????????????????????????????D.?655
5.如图,在⊙O中,∠ABC=130°,则∠AOC等于( )
?
A.?50°??????????????????????????????????????B.?80°??????????????????????????????????????C.?90°??????????????????????????????????????D.?100°
6.如图是某个球放进盒子内的截面图,球的一部分露出盒子外,已知⊙O交矩形ABCD的边AD于点E,F,已知AB=EF=2,则球的半径长为(?? )
A.?32??????????????????????????????????????????B.?43??????????????????????????????????????????C.?54??????????????????????????????????????????D.?65
7.在Rt△ABC中,∠ACB = 90°,AC = 9,BC = 12,则其外接圆的半径为(?? )
A.?15??????????????????????????????????????????B.?7.5??????????????????????????????????????????C.?6??????????????????????????????????????????D.?3
8.如图,点A,B,C在 ⊙O 上,且 ∠BAC=25° ,则 ∠OCB 的度数是(?? )
A.?65°????????????????????????????????????B.?55°????????????????????????????????????C.?70°????????????????????????????????????D.?50°
9.已知点O是 △ABC 的外心,作正方形 OCDE ,下列说法:①点O是 △AEB 的外心;②点O是 △ADC 的外心;③点O是 △BCE 的外心;④点O是 △ADB 的外心.其中说法一定正确的是(?? )
A.?②④??????????????????????????????????B.?①③??????????????????????????????????C.?②③④??????????????????????????????????D.?①③④
10.如图,圆 O 为 △ABC 的外接圆, ∠A=72° ,则 ∠BCO 的度数为(?? )
A.?15°???????????????????????????????????????B.?18°???????????????????????????????????????C.?28°???????????????????????????????????????D.?30°
11.已知四边形ABCD,下列命题:①若 ∠A+∠C=180° ,则四边形ABCD一定存在外接圆;②若四边形ABCD内存在一点到四个顶点的距离相等,则 ∠A+∠C=∠B+∠D ;③若四边形ABCD内存在一点到四条边的距离相等,则 AB+CD=BC+AD ,其中,真命题的个数为(?? )
A.?0???????????????????????????????????????????B.?1???????????????????????????????????????????C.?2???????????????????????????????????????????D.?3
12.如图,AB是⊙O的直径,BC是⊙O的切线.点D、E在⊙O上,若∠CBD=110°,则∠E的度数是(?? )
A.?90°???????????????????????????????????????B.?80°???????????????????????????????????????C.?70°???????????????????????????????????????D.?60°
二、填空题
13.在平面直角坐标系中,直线y=﹣x+6分别与x轴、y轴交于点A、B两点,点C在y轴左边,且∠ACB=90°,则点C的横坐标xc的取值范围是________.
14.如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,连接AC.若∠CAB=22.5°,CD=8cm,则⊙O的半径为________ cm.
15.如图,在 Rt△ABC 中, ∠ACB=90° , ∠BAC=30° , AC=4 ,P是 △ABC 所在平面内一点,且满足 PA⊥PC ,则 PB 的最大值为________.
16.已知 ⊙O 的半径为 10cm , OP=8cm ,则点P在 ⊙O 的________.(填“上面”“内部”或“外部”)
17.如图,在⊙O的内接四边形ABCD中,∠A=70°,∠OBC=60°,则∠ODC=________.
18.如图,已知点 M 在 y 轴正半轴上,圆 M 与 x 轴相切于原点 O ,平行于 y 轴的直线交圆 M 于 PQ 两点,点 P 在点 Q 的下方,且点 P 的坐标是 (2,1) ,则圆 M 的半径为________.
19.如图,在圆内接四边形ABCD中, ∠A 、 ∠B 、 ∠C 的度数之比为 2:4:7 ,则 ∠D= ________.
20.如图,在平面直角坐标系中,一个圆经过 O(0,0) , A(3,5) , B(6,0) 三点,则该圆的圆心的坐标是________.
三、综合题
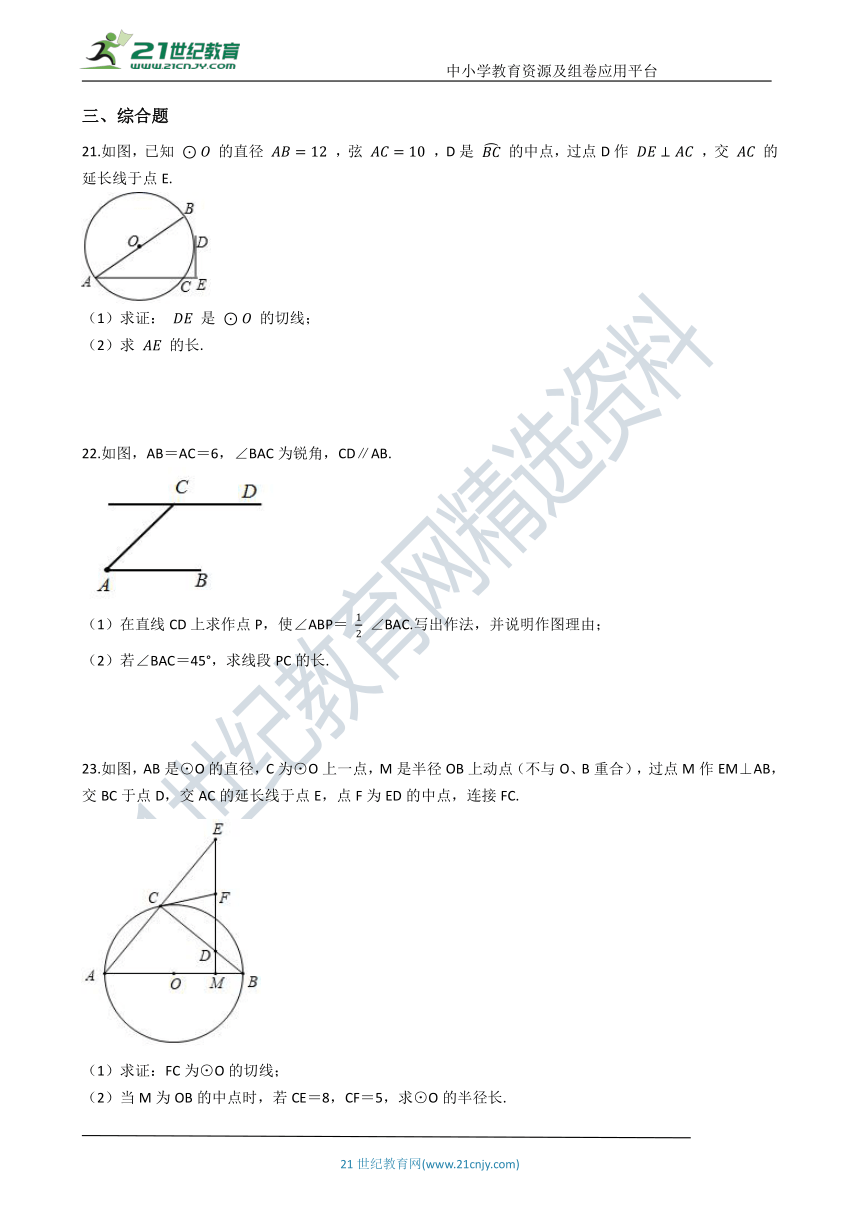
21.如图,已知 ⊙O 的直径 AB=12 ,弦 AC=10 ,D是 BC 的中点,过点D作 DE⊥AC ,交 AC 的延长线于点E.
(1)求证: DE 是 ⊙O 的切线;
(2)求 AE 的长.
22.如图,AB=AC=6,∠BAC为锐角,CD∥AB.
(1)在直线CD上求作点P,使∠ABP= 12 ∠BAC.写出作法,并说明作图理由;
(2)若∠BAC=45°,求线段PC的长.
23.如图,AB是⊙O的直径,C为⊙O上一点,M是半径OB上动点(不与O、B重合),过点M作EM⊥AB,交BC于点D,交AC的延长线于点E,点F为ED的中点,连接FC.
(1)求证:FC为⊙O的切线;
(2)当M为OB的中点时,若CE=8,CF=5,求⊙O的半径长.
24.如图, PA 是 ⊙O 的切线,A为切点,点B、C、D在 ⊙O 上,且 PA=PB .
(1)求证: PB 是 ⊙O 的切线;
(2)若 ∠P=100° ,则 ∠B+∠D 的度数为________°.
25.如图,在 ?ABCD 中,E是AD上一点,延长CE到点F,使得 ∠FBC=∠DCE .
(1)求证: ∠D=∠F ;
(2)请用无刻度直尺与圆规在AD上求作一点P,使 ∠BPC=∠D .(保留作图痕迹,不写作法)
答案解析部分
一、单选题
1.【答案】 C
解:如图,
∵ BC//OA , ∠A=20°
∴ ∠C=∠A=20°
∴ ∠O=2∠C=40°
∵BC//OA, ?
∴ ∠B=∠O=40°
故答案为:C.
2.【答案】 B
解:连接AG、GE、EC,则四边形ACEG为正方形,故AEAC=2 .
故选B.
3.【答案】 D
解:连接OC,如图所示,
∵OB=OC,
∴∠OCB=∠OBC=40°,
∴∠BOC=100°,
∵∠1+∠BOC=360°,
∴∠1=260°,
∵∠A= 12 ∠1,
∴∠A=130°.
故答案为:D.
4.【答案】 A
解:过点 C 作 CP⊥ 直线 l ,交圆 C 于 Q 点,此时 PQ 的值最小,连接 BC 、 AC ,作 CM⊥OA 于 M , CN⊥OB 于 N ,
∵ y=?2x+6 ,
∴ A(3,0) , B(0,6) ,
∴ OA=3 , OB=6 ,
∴ AB=32+62=35 ,
∵四边形 OMCN 是正方形,
∴ OM=ON=1 ,
∴ AM=3?1=2 , BN=6?1=5 ,
设 PC=d , PB=m ,则 AP=35?m ,
∵ BN2+CN2=BC2=PB2+PC2 , AM2+CM2=AC2=AP2+CP2 ,
∴ 52+12=m2+d2 , 22+12=(35?m)2+d2 ,
解得: d=355 ,
∵ ⊙C 的半径为1,
∴ PQ=355?1 ,
故答案为:A.
5.【答案】 D
解:∠1=2∠ABC=2×130°=260°,
则∠AOC=360°﹣∠1=360°﹣260°=100°.
故选D.
6.【答案】 C
解:由题意得:⊙O与BC相切,记切点为G,作直线OG,分别交AD、劣弧 EF 于点H、I,连接OF,如图所示:
∵四边形ABCD是矩形,
∴AD // BC,
∵IG⊥BC,
∴IG⊥AD,
∴FH= 12 EF=1,
∵四边形ABCD是矩形,
∴HA⊥AB,
∴AB⊥BG,
∵IG⊥BC,
∴四边形ABGH是矩形,
∴GH=AB=2,
设⊙O的半径为r,则OH=2﹣r,
在Rt△OFH中,由勾股定理得:
r2?(2?r)2=1 ,
解得:r= 54 ,
即球的半径长为 54 ,
故答案为:C.
7.【答案】 B
解: ∵∠ACB=90°,
∴AB2=AC2+BC2 , 而AC=9,BC=12,
∴AB= 92+122 =15.
又∵AB是Rt△ABC的外接圆的直径,
∴其外接圆的半径为7.5.
故答案为:B.
8.【答案】 A
解:连接OB,
∵OB=OC,∠BOC=2∠BAC=2×25°=50°,
∴∠OCB=∠OBC= 12 (180°-50°)=65°.
故答案为:A.
9.【答案】 B
解:连接OB、OD、OA,
∵O为三角形ABC的外心,
∴OA=OC=OB,
∵四边形OCDE为正方形,
∴OE=OC<OD,
∴OA=OB=OC=OE≠OD,
∴OA=OE=OB,即O是△AEB的外心,故①正确;
OA=OC≠OD,即O不是△ADC的外心,故②错误;
OB=OC=OE,即O是△BCE的外心,故③正确;
OB=OA≠OD,即O不是△ABD的外心,故④错误;
故答案为:B.
10.【答案】 B
解:连接OB,
∵ ∠A=72° ,
∴∠BOC=2∠A=144°,
∵OB=OC,
∴∠OCB=∠OBC= 12 (180-144)=18°,
故答案为:B.
11.【答案】 D
解:①在四边形ABCD中,∠A+∠B+∠C+∠D=360?,
∵ ∠A+∠C=180° ,
∴∠B+∠D=180?,
则四边形ABCD一定存在外接圆,
过A,B,D作圆O,假设C不在圆O上,点C在圆外或圆内,若点C在圆外,设BC交圆O于C',连结DC',
根据圆内接四边形的性质得∠A+∠DC'B=180°,
∵∠A+∠C=180°,
∴∠DC'B=∠C,
这与三角形外角定理矛盾,故C不可能在圆外,
类似地可证C不可能在圆内,
∴C在圆O上,也即A,B,C,D四点共圆,
若 ∠A+∠C=180° ,则四边形ABCD一定存在外接圆是真命题,
②若四边形ABCD内存在一点到四个顶点的距离相等,
∴A、B、C、D四点在同一圆上,
由圆内接四边形的性质得∠A+∠C=180°,∠B+∠D=180°,
∴ ∠A+∠C=∠B+∠D ;
若四边形ABCD内存在一点到四个顶点的距离相等,则 ∠A+∠C=∠B+∠D 是真命题;
③若四边形ABCD内存在一点到四条边的距离相等,设点O到向四边作垂线,OE⊥AD于E,OF⊥AB于F,OG⊥BC于G,OH⊥CD于H,
由题意知:OE=OF=OG=OH,
∴E、F、G、H四点在同一圆上,
由切线的判定定理知,
AB、BC、CD、DA是圆的切线,
由切线的性质知AE=AF;BF=BG;CG=CH,DH=DE,
AB+CD=AF+BF+CH+DH=AE+BG+CG+DE=(AE+DE)+(BG+CG)=AD+BC,
则 AB+CD=BC+AD ,
若四边形ABCD内存在一点到四条边的距离相等,则 AB+CD=BC+AD 是真命题.
故答案为:D.
12.【答案】 C
解: BC 是 ⊙O 的切线.
∴∠ABC=90?,
∵∠CBD=110°,
∴∠ABD=20?.
∵ AB 是 ⊙O 的直径,
∴∠ADB=90?
∴∠BAD=90°?20°=70°
∴∠E=∠BAD=70?
故答案为:C.
二、填空题
13.【答案】 3?32≤xC<0
解:由题意可得如图所示:
∵直线y=﹣x+6分别与x轴、y轴交于点A、B两点,
∴ A(6,0),B(0,6) ,
∴ OA=OB=6 ,
∴ AB=OA2+OB2=62 ,
∵∠ACB=90°,
∴点C位于以AB为直径,AB的中点D为圆心的圆上,
过点D作DE⊥y轴并延长,交y轴与⊙D分别于点E、C,此时∠ACB=90°,并且此时点C横坐标为最大,
∴DE∥x轴,OE=BE,
∴ DE=12OB=3 ,
∴ CE=32?3 ,
∴点C横坐标xc的取值范围是 3?32≤xC<0
故答案为: 3?32≤xC<0 .
14.【答案】 32
解:连接OC,如图所示:
∵AB是O的直径,弦CD⊥AB,
∴CE=DE= 12 CD=3cm,
∵弧BC=弧BC, ∠CAB=22.5°
∴∠COE=2∠CAB=45°,
∴△COE为等腰直角三角形,
∴OC= 2 CE= 32 cm,
故答案为: 32 .
15.【答案】 2213 +2
解:∵∠ACB=90°,∠BAC=30°,
∴AB=2BC,又AC=4,
∴ BC2+42=(2BC)2 ,
解得:BC= 433 ,
∵PA⊥PC,即∠APC=90°,
∴点P在以AC为直径的圆O上,
如图,当P、O、B三点共线时,PB最大,
∵BC= 433 ,OC= 12 AC=2,
∴BO= BC2+OC2 = 2213 ,
∴PB= 2213 +2,
故答案为: 2213 +2.
16.【答案】 内部
解:∵点P到圆心的距离OP=8cm,小于⊙O的半径10cm,
∴点P在圆内部.
故答案为:内部.
17.【答案】 50°
解:∵∠A=70°
∴∠C=180°﹣∠A=110°,
∴∠BOD=2∠A=140°,
∵∠OBC=60°,
∴∠ODC=360°﹣110°﹣140°﹣60°=50°,
故答案为:50°.
18.【答案】 52
解:如图,设圆 M 的半径为r,圆 M与y轴的另一交点为N,则N的坐标为(0,2r),连结PN、OP,
由题意可得:
OP2+PN2=ON2 ,
∴ 5+4+(2r?1)2=(2r)2 ,
解之得: r=52 ,
故答案为 52 .
19.【答案】 100°
解:∵四边形ABCD是圆内接四边形,
∴∠B+∠D=∠A+∠C=180°,
∵∠A、∠B、∠C的度数之比为2:4:7,
∴∠A=180°× 29 =40°,∠C=180°× 79 =140°,
∠B=180°× 49 =80°,
∴∠D=180°﹣80°=100°,
故答案为:100°.
20.【答案】 (3,1.6)
解:根据题意得,圆心在线段OB的垂直平分线上,设圆心 O′(3,m) ,过点A作 AO′⊥OB 垂足为C,
∵OO′=O′A ,由勾股定理得
∴32+m2=(5?m)2
∴9+m2=25?10m+m2
解得 m=1.6
∴O′(3,1.6)
故答案为: (3,1.6) .
三、综合题
21.【答案】 (1)证明:连接 OD ,
∵D为 BC 的中点,
∴ BD=CD ,
∴ ∠BOD=∠BAE ,
∴ OD//AE ,
∵ DE⊥AC ,
∴ ∠AED=90° ,
∴ ∠ODE=90° ,
∴ OD⊥DE ,
则 DE 为圆O的切线;
(2)解:过点O作 OF⊥AC ,
∵ AC=10 ,
∴ AF=CF=12AC=5 ,
∵ ∠OFE=∠DEF=∠ODE=90° ,
∴四边形 OFED 为矩形,
∴ FE=OD=12AB ,
∵ AB=12 ,
∴ FE=6 ,
则 AE=AF+FE=5+6=11
22.【答案】 (1)解:延长BA,且取BA的延长线上的一点 B′ ,使 B′A=BA ,以点A为圆心AB为半径画半圆,半圆交直线CD于一点,即点P,连接 B′A ,PA,PB,此时的∠ABP= 12 ∠BAC,
如图:
理由如下:∵AB∥CD
∴∠ABP=∠BPC
∵∠BPC= 12 ∠BAC
∴∠ABP= 12 ∠BAC
(2)解:由(1)得∠ABP= 12 ∠BAC
∵∠BAC=2∠ABP,且AB=AP
∴∠ABP=∠APB=∠BPC= 12 ∠BAC=22.5?
∵三角形的内角和为180?
∴∠BAP+∠ABP+∠APB=180?,即∠BAC+∠PAC+∠ABP+∠APB=180?,
∴∠PAC=90?,又AB=AC=6,
∴PC= AC2+AP2=62 ,
故PC的长为 62 .
23.【答案】 (1)证明:如图,连接OC,
∵OB=OC,
∴∠OBC=∠OCB,
∵EM⊥AB,
∴∠BME=90°,
∴∠OBC+∠BDM=90°,
∵AB是⊙O的直径,
∴∠ACB=∠ECD=90°,
∵F是DE的中点,
∴FC=FD,∠FCD=∠FDC,
∵∠FDC=∠BDM,
∴∠OCB+∠FCD=90°,
∴OC⊥FC,
∴FC是⊙O的切线;
(2)解:∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠BCE=90°,
∴∠FCE+∠DCF=90°,
∵∠CDF+∠E=90°,∠DCF=∠CDF,
∴∠E=∠FCE,
∴CF=EF=5,
∴DF=CF=5,
∴CD= DE2?CE2=102?82=6 ,
∴tan∠CDE= CECD=86=43 ,
∵∠BDM=∠CDE,
∴tan∠BDM= 43 ,
设⊙O的半径为R,则BM= 12R ,
∴DM= 38R ,
连接OF,
∵ OF2=OC2+CF2=OM2+FM2 ,
∴ R2+52=(12R)2+(5+38R)2 ,
解得: R=8013 .
24.【答案】 (1)证明:连接 OA , OB , OP
∵ PA 是 ⊙O 的切线,A为切点
∴ ∠PAO=90°
在 △PBO 和 △PAO 中,
∵ PB=PA , OB=OA , OP=OP
∴ △PBO≌△PAO
∴ ∠PBO=∠PAO=90°
∴ PB⊥BO ,且 PB 过半径 OB 的外端
∴ PB 是 ⊙O 的切线.
(2)220
解:(2)连接 AB
由(1)可知 PB=PA ,
∴ ∠PAB=∠PBA=180°?∠P2=40° ,
圆内接四边形 ABCD 中 ∠D+∠ABC=180°
∴ ∠D+∠PBC=∠D+∠ABC+∠PBA=220° .
故答案为:220.
25.【答案】 (1)证明:∵四边形ABCD 是平行四边形,
∴AD∥BC.
∴∠CED=∠BCF.
∵∠CED+∠DCE+∠D=180°,∠BCF+∠FBC+∠F=180°,
∴∠D=180°?∠CED?∠DCE,∠F=180°?∠BCF?∠FBC.
又∵∠DCE=∠FBC,
∴∠D=∠F;
(2)解:图中P 就是所求作的点.
一、单选题
1.如图,点 A , B , C 在 ⊙O 上, BC//OA , ∠A=20° ,则 ∠B 的度数为(?? )
A.?10°????????????????????????????????????B.?20°????????????????????????????????????C.?40°????????????????????????????????????D.?50°
2.如图,在正八边形ABCDEFGH中,连接AC,AE,则AEAC的值是( )
A.?1?????????????????????????????????????????B.?2?????????????????????????????????????????C.?2?????????????????????????????????????????D.?3?
3.如图,△ABC内接于⊙O,∠OBC=40°,则∠A的度数为( ??)
A.?80°?????????????????????????????????????B.?100°?????????????????????????????????????C.?110°?????????????????????????????????????D.?130°
4.如图, ⊙C 的圆心 C 的坐标为 (1,1) ,半径为1,直线 l 的表达式为 y=?2x+6 , P 是直线 l 上的动点, Q 是 ⊙C 上的动点,则 PQ 的最小值是(?? )
A.?355?1????????????????????????????????B.?655?1????????????????????????????????C.?355????????????????????????????????D.?655
5.如图,在⊙O中,∠ABC=130°,则∠AOC等于( )
?
A.?50°??????????????????????????????????????B.?80°??????????????????????????????????????C.?90°??????????????????????????????????????D.?100°
6.如图是某个球放进盒子内的截面图,球的一部分露出盒子外,已知⊙O交矩形ABCD的边AD于点E,F,已知AB=EF=2,则球的半径长为(?? )
A.?32??????????????????????????????????????????B.?43??????????????????????????????????????????C.?54??????????????????????????????????????????D.?65
7.在Rt△ABC中,∠ACB = 90°,AC = 9,BC = 12,则其外接圆的半径为(?? )
A.?15??????????????????????????????????????????B.?7.5??????????????????????????????????????????C.?6??????????????????????????????????????????D.?3
8.如图,点A,B,C在 ⊙O 上,且 ∠BAC=25° ,则 ∠OCB 的度数是(?? )
A.?65°????????????????????????????????????B.?55°????????????????????????????????????C.?70°????????????????????????????????????D.?50°
9.已知点O是 △ABC 的外心,作正方形 OCDE ,下列说法:①点O是 △AEB 的外心;②点O是 △ADC 的外心;③点O是 △BCE 的外心;④点O是 △ADB 的外心.其中说法一定正确的是(?? )
A.?②④??????????????????????????????????B.?①③??????????????????????????????????C.?②③④??????????????????????????????????D.?①③④
10.如图,圆 O 为 △ABC 的外接圆, ∠A=72° ,则 ∠BCO 的度数为(?? )
A.?15°???????????????????????????????????????B.?18°???????????????????????????????????????C.?28°???????????????????????????????????????D.?30°
11.已知四边形ABCD,下列命题:①若 ∠A+∠C=180° ,则四边形ABCD一定存在外接圆;②若四边形ABCD内存在一点到四个顶点的距离相等,则 ∠A+∠C=∠B+∠D ;③若四边形ABCD内存在一点到四条边的距离相等,则 AB+CD=BC+AD ,其中,真命题的个数为(?? )
A.?0???????????????????????????????????????????B.?1???????????????????????????????????????????C.?2???????????????????????????????????????????D.?3
12.如图,AB是⊙O的直径,BC是⊙O的切线.点D、E在⊙O上,若∠CBD=110°,则∠E的度数是(?? )
A.?90°???????????????????????????????????????B.?80°???????????????????????????????????????C.?70°???????????????????????????????????????D.?60°
二、填空题
13.在平面直角坐标系中,直线y=﹣x+6分别与x轴、y轴交于点A、B两点,点C在y轴左边,且∠ACB=90°,则点C的横坐标xc的取值范围是________.
14.如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,连接AC.若∠CAB=22.5°,CD=8cm,则⊙O的半径为________ cm.
15.如图,在 Rt△ABC 中, ∠ACB=90° , ∠BAC=30° , AC=4 ,P是 △ABC 所在平面内一点,且满足 PA⊥PC ,则 PB 的最大值为________.
16.已知 ⊙O 的半径为 10cm , OP=8cm ,则点P在 ⊙O 的________.(填“上面”“内部”或“外部”)
17.如图,在⊙O的内接四边形ABCD中,∠A=70°,∠OBC=60°,则∠ODC=________.
18.如图,已知点 M 在 y 轴正半轴上,圆 M 与 x 轴相切于原点 O ,平行于 y 轴的直线交圆 M 于 PQ 两点,点 P 在点 Q 的下方,且点 P 的坐标是 (2,1) ,则圆 M 的半径为________.
19.如图,在圆内接四边形ABCD中, ∠A 、 ∠B 、 ∠C 的度数之比为 2:4:7 ,则 ∠D= ________.
20.如图,在平面直角坐标系中,一个圆经过 O(0,0) , A(3,5) , B(6,0) 三点,则该圆的圆心的坐标是________.
三、综合题
21.如图,已知 ⊙O 的直径 AB=12 ,弦 AC=10 ,D是 BC 的中点,过点D作 DE⊥AC ,交 AC 的延长线于点E.
(1)求证: DE 是 ⊙O 的切线;
(2)求 AE 的长.
22.如图,AB=AC=6,∠BAC为锐角,CD∥AB.
(1)在直线CD上求作点P,使∠ABP= 12 ∠BAC.写出作法,并说明作图理由;
(2)若∠BAC=45°,求线段PC的长.
23.如图,AB是⊙O的直径,C为⊙O上一点,M是半径OB上动点(不与O、B重合),过点M作EM⊥AB,交BC于点D,交AC的延长线于点E,点F为ED的中点,连接FC.
(1)求证:FC为⊙O的切线;
(2)当M为OB的中点时,若CE=8,CF=5,求⊙O的半径长.
24.如图, PA 是 ⊙O 的切线,A为切点,点B、C、D在 ⊙O 上,且 PA=PB .
(1)求证: PB 是 ⊙O 的切线;
(2)若 ∠P=100° ,则 ∠B+∠D 的度数为________°.
25.如图,在 ?ABCD 中,E是AD上一点,延长CE到点F,使得 ∠FBC=∠DCE .
(1)求证: ∠D=∠F ;
(2)请用无刻度直尺与圆规在AD上求作一点P,使 ∠BPC=∠D .(保留作图痕迹,不写作法)
答案解析部分
一、单选题
1.【答案】 C
解:如图,
∵ BC//OA , ∠A=20°
∴ ∠C=∠A=20°
∴ ∠O=2∠C=40°
∵BC//OA, ?
∴ ∠B=∠O=40°
故答案为:C.
2.【答案】 B
解:连接AG、GE、EC,则四边形ACEG为正方形,故AEAC=2 .
故选B.
3.【答案】 D
解:连接OC,如图所示,
∵OB=OC,
∴∠OCB=∠OBC=40°,
∴∠BOC=100°,
∵∠1+∠BOC=360°,
∴∠1=260°,
∵∠A= 12 ∠1,
∴∠A=130°.
故答案为:D.
4.【答案】 A
解:过点 C 作 CP⊥ 直线 l ,交圆 C 于 Q 点,此时 PQ 的值最小,连接 BC 、 AC ,作 CM⊥OA 于 M , CN⊥OB 于 N ,
∵ y=?2x+6 ,
∴ A(3,0) , B(0,6) ,
∴ OA=3 , OB=6 ,
∴ AB=32+62=35 ,
∵四边形 OMCN 是正方形,
∴ OM=ON=1 ,
∴ AM=3?1=2 , BN=6?1=5 ,
设 PC=d , PB=m ,则 AP=35?m ,
∵ BN2+CN2=BC2=PB2+PC2 , AM2+CM2=AC2=AP2+CP2 ,
∴ 52+12=m2+d2 , 22+12=(35?m)2+d2 ,
解得: d=355 ,
∵ ⊙C 的半径为1,
∴ PQ=355?1 ,
故答案为:A.
5.【答案】 D
解:∠1=2∠ABC=2×130°=260°,
则∠AOC=360°﹣∠1=360°﹣260°=100°.
故选D.
6.【答案】 C
解:由题意得:⊙O与BC相切,记切点为G,作直线OG,分别交AD、劣弧 EF 于点H、I,连接OF,如图所示:
∵四边形ABCD是矩形,
∴AD // BC,
∵IG⊥BC,
∴IG⊥AD,
∴FH= 12 EF=1,
∵四边形ABCD是矩形,
∴HA⊥AB,
∴AB⊥BG,
∵IG⊥BC,
∴四边形ABGH是矩形,
∴GH=AB=2,
设⊙O的半径为r,则OH=2﹣r,
在Rt△OFH中,由勾股定理得:
r2?(2?r)2=1 ,
解得:r= 54 ,
即球的半径长为 54 ,
故答案为:C.
7.【答案】 B
解: ∵∠ACB=90°,
∴AB2=AC2+BC2 , 而AC=9,BC=12,
∴AB= 92+122 =15.
又∵AB是Rt△ABC的外接圆的直径,
∴其外接圆的半径为7.5.
故答案为:B.
8.【答案】 A
解:连接OB,
∵OB=OC,∠BOC=2∠BAC=2×25°=50°,
∴∠OCB=∠OBC= 12 (180°-50°)=65°.
故答案为:A.
9.【答案】 B
解:连接OB、OD、OA,
∵O为三角形ABC的外心,
∴OA=OC=OB,
∵四边形OCDE为正方形,
∴OE=OC<OD,
∴OA=OB=OC=OE≠OD,
∴OA=OE=OB,即O是△AEB的外心,故①正确;
OA=OC≠OD,即O不是△ADC的外心,故②错误;
OB=OC=OE,即O是△BCE的外心,故③正确;
OB=OA≠OD,即O不是△ABD的外心,故④错误;
故答案为:B.
10.【答案】 B
解:连接OB,
∵ ∠A=72° ,
∴∠BOC=2∠A=144°,
∵OB=OC,
∴∠OCB=∠OBC= 12 (180-144)=18°,
故答案为:B.
11.【答案】 D
解:①在四边形ABCD中,∠A+∠B+∠C+∠D=360?,
∵ ∠A+∠C=180° ,
∴∠B+∠D=180?,
则四边形ABCD一定存在外接圆,
过A,B,D作圆O,假设C不在圆O上,点C在圆外或圆内,若点C在圆外,设BC交圆O于C',连结DC',
根据圆内接四边形的性质得∠A+∠DC'B=180°,
∵∠A+∠C=180°,
∴∠DC'B=∠C,
这与三角形外角定理矛盾,故C不可能在圆外,
类似地可证C不可能在圆内,
∴C在圆O上,也即A,B,C,D四点共圆,
若 ∠A+∠C=180° ,则四边形ABCD一定存在外接圆是真命题,
②若四边形ABCD内存在一点到四个顶点的距离相等,
∴A、B、C、D四点在同一圆上,
由圆内接四边形的性质得∠A+∠C=180°,∠B+∠D=180°,
∴ ∠A+∠C=∠B+∠D ;
若四边形ABCD内存在一点到四个顶点的距离相等,则 ∠A+∠C=∠B+∠D 是真命题;
③若四边形ABCD内存在一点到四条边的距离相等,设点O到向四边作垂线,OE⊥AD于E,OF⊥AB于F,OG⊥BC于G,OH⊥CD于H,
由题意知:OE=OF=OG=OH,
∴E、F、G、H四点在同一圆上,
由切线的判定定理知,
AB、BC、CD、DA是圆的切线,
由切线的性质知AE=AF;BF=BG;CG=CH,DH=DE,
AB+CD=AF+BF+CH+DH=AE+BG+CG+DE=(AE+DE)+(BG+CG)=AD+BC,
则 AB+CD=BC+AD ,
若四边形ABCD内存在一点到四条边的距离相等,则 AB+CD=BC+AD 是真命题.
故答案为:D.
12.【答案】 C
解: BC 是 ⊙O 的切线.
∴∠ABC=90?,
∵∠CBD=110°,
∴∠ABD=20?.
∵ AB 是 ⊙O 的直径,
∴∠ADB=90?
∴∠BAD=90°?20°=70°
∴∠E=∠BAD=70?
故答案为:C.
二、填空题
13.【答案】 3?32≤xC<0
解:由题意可得如图所示:
∵直线y=﹣x+6分别与x轴、y轴交于点A、B两点,
∴ A(6,0),B(0,6) ,
∴ OA=OB=6 ,
∴ AB=OA2+OB2=62 ,
∵∠ACB=90°,
∴点C位于以AB为直径,AB的中点D为圆心的圆上,
过点D作DE⊥y轴并延长,交y轴与⊙D分别于点E、C,此时∠ACB=90°,并且此时点C横坐标为最大,
∴DE∥x轴,OE=BE,
∴ DE=12OB=3 ,
∴ CE=32?3 ,
∴点C横坐标xc的取值范围是 3?32≤xC<0
故答案为: 3?32≤xC<0 .
14.【答案】 32
解:连接OC,如图所示:
∵AB是O的直径,弦CD⊥AB,
∴CE=DE= 12 CD=3cm,
∵弧BC=弧BC, ∠CAB=22.5°
∴∠COE=2∠CAB=45°,
∴△COE为等腰直角三角形,
∴OC= 2 CE= 32 cm,
故答案为: 32 .
15.【答案】 2213 +2
解:∵∠ACB=90°,∠BAC=30°,
∴AB=2BC,又AC=4,
∴ BC2+42=(2BC)2 ,
解得:BC= 433 ,
∵PA⊥PC,即∠APC=90°,
∴点P在以AC为直径的圆O上,
如图,当P、O、B三点共线时,PB最大,
∵BC= 433 ,OC= 12 AC=2,
∴BO= BC2+OC2 = 2213 ,
∴PB= 2213 +2,
故答案为: 2213 +2.
16.【答案】 内部
解:∵点P到圆心的距离OP=8cm,小于⊙O的半径10cm,
∴点P在圆内部.
故答案为:内部.
17.【答案】 50°
解:∵∠A=70°
∴∠C=180°﹣∠A=110°,
∴∠BOD=2∠A=140°,
∵∠OBC=60°,
∴∠ODC=360°﹣110°﹣140°﹣60°=50°,
故答案为:50°.
18.【答案】 52
解:如图,设圆 M 的半径为r,圆 M与y轴的另一交点为N,则N的坐标为(0,2r),连结PN、OP,
由题意可得:
OP2+PN2=ON2 ,
∴ 5+4+(2r?1)2=(2r)2 ,
解之得: r=52 ,
故答案为 52 .
19.【答案】 100°
解:∵四边形ABCD是圆内接四边形,
∴∠B+∠D=∠A+∠C=180°,
∵∠A、∠B、∠C的度数之比为2:4:7,
∴∠A=180°× 29 =40°,∠C=180°× 79 =140°,
∠B=180°× 49 =80°,
∴∠D=180°﹣80°=100°,
故答案为:100°.
20.【答案】 (3,1.6)
解:根据题意得,圆心在线段OB的垂直平分线上,设圆心 O′(3,m) ,过点A作 AO′⊥OB 垂足为C,
∵OO′=O′A ,由勾股定理得
∴32+m2=(5?m)2
∴9+m2=25?10m+m2
解得 m=1.6
∴O′(3,1.6)
故答案为: (3,1.6) .
三、综合题
21.【答案】 (1)证明:连接 OD ,
∵D为 BC 的中点,
∴ BD=CD ,
∴ ∠BOD=∠BAE ,
∴ OD//AE ,
∵ DE⊥AC ,
∴ ∠AED=90° ,
∴ ∠ODE=90° ,
∴ OD⊥DE ,
则 DE 为圆O的切线;
(2)解:过点O作 OF⊥AC ,
∵ AC=10 ,
∴ AF=CF=12AC=5 ,
∵ ∠OFE=∠DEF=∠ODE=90° ,
∴四边形 OFED 为矩形,
∴ FE=OD=12AB ,
∵ AB=12 ,
∴ FE=6 ,
则 AE=AF+FE=5+6=11
22.【答案】 (1)解:延长BA,且取BA的延长线上的一点 B′ ,使 B′A=BA ,以点A为圆心AB为半径画半圆,半圆交直线CD于一点,即点P,连接 B′A ,PA,PB,此时的∠ABP= 12 ∠BAC,
如图:
理由如下:∵AB∥CD
∴∠ABP=∠BPC
∵∠BPC= 12 ∠BAC
∴∠ABP= 12 ∠BAC
(2)解:由(1)得∠ABP= 12 ∠BAC
∵∠BAC=2∠ABP,且AB=AP
∴∠ABP=∠APB=∠BPC= 12 ∠BAC=22.5?
∵三角形的内角和为180?
∴∠BAP+∠ABP+∠APB=180?,即∠BAC+∠PAC+∠ABP+∠APB=180?,
∴∠PAC=90?,又AB=AC=6,
∴PC= AC2+AP2=62 ,
故PC的长为 62 .
23.【答案】 (1)证明:如图,连接OC,
∵OB=OC,
∴∠OBC=∠OCB,
∵EM⊥AB,
∴∠BME=90°,
∴∠OBC+∠BDM=90°,
∵AB是⊙O的直径,
∴∠ACB=∠ECD=90°,
∵F是DE的中点,
∴FC=FD,∠FCD=∠FDC,
∵∠FDC=∠BDM,
∴∠OCB+∠FCD=90°,
∴OC⊥FC,
∴FC是⊙O的切线;
(2)解:∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠BCE=90°,
∴∠FCE+∠DCF=90°,
∵∠CDF+∠E=90°,∠DCF=∠CDF,
∴∠E=∠FCE,
∴CF=EF=5,
∴DF=CF=5,
∴CD= DE2?CE2=102?82=6 ,
∴tan∠CDE= CECD=86=43 ,
∵∠BDM=∠CDE,
∴tan∠BDM= 43 ,
设⊙O的半径为R,则BM= 12R ,
∴DM= 38R ,
连接OF,
∵ OF2=OC2+CF2=OM2+FM2 ,
∴ R2+52=(12R)2+(5+38R)2 ,
解得: R=8013 .
24.【答案】 (1)证明:连接 OA , OB , OP
∵ PA 是 ⊙O 的切线,A为切点
∴ ∠PAO=90°
在 △PBO 和 △PAO 中,
∵ PB=PA , OB=OA , OP=OP
∴ △PBO≌△PAO
∴ ∠PBO=∠PAO=90°
∴ PB⊥BO ,且 PB 过半径 OB 的外端
∴ PB 是 ⊙O 的切线.
(2)220
解:(2)连接 AB
由(1)可知 PB=PA ,
∴ ∠PAB=∠PBA=180°?∠P2=40° ,
圆内接四边形 ABCD 中 ∠D+∠ABC=180°
∴ ∠D+∠PBC=∠D+∠ABC+∠PBA=220° .
故答案为:220.
25.【答案】 (1)证明:∵四边形ABCD 是平行四边形,
∴AD∥BC.
∴∠CED=∠BCF.
∵∠CED+∠DCE+∠D=180°,∠BCF+∠FBC+∠F=180°,
∴∠D=180°?∠CED?∠DCE,∠F=180°?∠BCF?∠FBC.
又∵∠DCE=∠FBC,
∴∠D=∠F;
(2)解:图中P 就是所求作的点.
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
