广东省佛山市三水区2012届高三5月考前金题巧练理科数学(6)
文档属性
| 名称 | 广东省佛山市三水区2012届高三5月考前金题巧练理科数学(6) |  | |
| 格式 | zip | ||
| 文件大小 | 278.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-05-24 12:22:00 | ||
图片预览




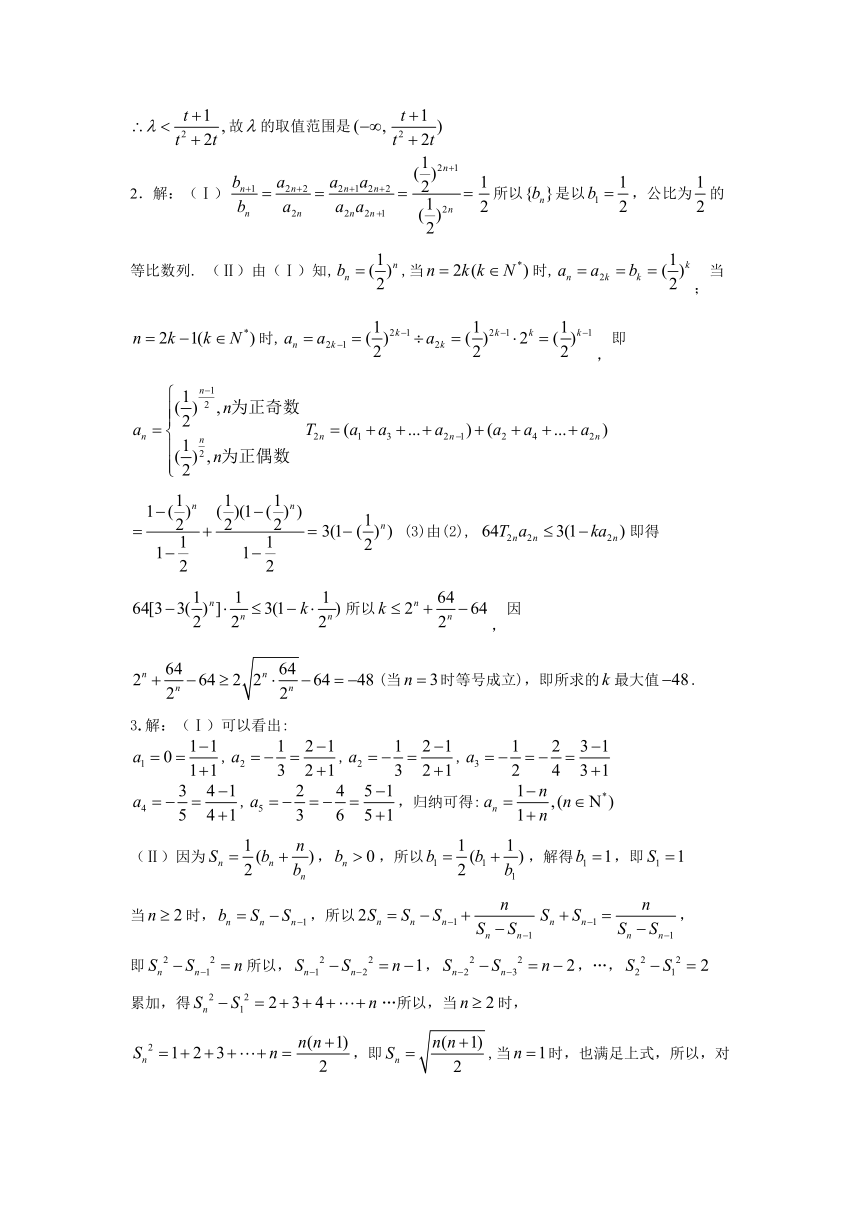
文档简介
2012考前金题巧练(6)
祝你成功
1.已知函数.
(Ⅰ)数列求数列的通项公式;
(Ⅱ)已知数列,求数列的通项公式;
(Ⅲ)设的前n项和为Sn,若不等式对所有的正整数n恒成立,求的取值范围。
2.已知数列中,,,记为的前项的和.
(Ⅰ)设,证明:数列是等比数列;(Ⅱ)求;
(Ⅲ)不等式对于一切恒成立,求实数的最大值.
3.已知数列的前五项依次是. 正数数列的前项和为,且.(Ⅰ)通过观察和归纳写出符合条件的数列的一个通项公式;
(Ⅱ)求的表达式;(Ⅲ)在(Ⅰ)、(Ⅱ)的条件下,,当时,设,是数列的前项和,且恒成立,求实数的取值范围.
4.已知点(1,)是函数且)的图象上一点,等比数列的前项和为,数列的首项为,且前项和满足-=+().(Ⅰ)求数列和的通项公式;
(Ⅱ)若数列{前项和为,问>的最小正整数是多少 .
5.已知:数列﹛﹜,﹛﹜中,=0,=1,且当时,,,成等差数列,,,成等比数列.(Ⅰ)求数列﹛﹜,﹛﹜的通项公式;
(Ⅱ)求最小自然数,使得当≥时,对任意实数,不等式≥恒成立; (Ⅲ)设 (∈),求证:当≥2都有>2.
6.直线过(1,0)点,且关于直线y=x对称的直线为,已知点在上,。当n≥2时,有
(Ⅰ)求的方程;(Ⅱ)求{ an}的通项公式;
(Ⅲ)设求数列{ bn}的前n项和Sn
7.已知数列{ an }的前n项和Sn满足,Sn=2an+(—1)n,n≥1。
(Ⅰ)求数列{ an }的通项公式;
(Ⅱ)求证:对任意整数m>4,有
8.已知函数(为常数,且),且数列是首项为4,公差为2的等差数列. (Ⅰ) 求证:数列是等比数列;(Ⅱ) 若,当时,求数列的前项和;(Ⅲ) 若,问是否存在实数,使得中的每一项恒小于它后面的项?若存在,求出的范围;若不存在,说明理由.
9.已知数列{an}满足:a1=a2=a3=2,an+1=a1a2…an-1(n≥3),记
(n≥3).
(Ⅰ)求证数列{bn}为等差数列,并求其通项公式;
(Ⅱ)设,数列{}的前n项和为Sn,求证:n10.已知数列中,.
(Ⅰ)写出的值(只写结果)并求出数列的通项公式;
(Ⅱ)设, 求的最大值。
11. 已知正项数列满足,,令.
(Ⅰ) 求证:数列为等比数列;
(Ⅱ) 记为数列的前项和,是否存在实数,使得不等式对恒成立?若存在,求出实数的取值范围;若不存在,请说明理由.
12.设数列
(Ⅰ)求数列的通项公式;
(Ⅱ)设,求数列
(Ⅲ)设,,记,设数列的前项和为,求证:对任意正整数都有;
2012考前金题巧练(6)参答
1. 解:(Ⅰ),
(Ⅱ)由已知得,
∴又所以的公比为2的等比数列,∴。
(Ⅲ) , 上是增函数
又不等式对所有的正整数n恒成立,故的取值范围是
2.解:(Ⅰ)所以是以,公比为的等比数列. (Ⅱ)由(Ⅰ)知,,当时,;当时,,即
(3)由(2), 即得所以,因(当时等号成立),即所求的最大值.
3.解:(Ⅰ)可以看出: ,,,
,,归纳可得:
(Ⅱ)因为,,所以,解得,即
当时,,所以,
即所以,,,…,
累加,得…所以,当时,,即,当时,也满足上式,所以,对所有,
(Ⅲ)在(Ⅰ)、(Ⅱ)的条件下,,当时,,当时,;当时
,因恒成立,即恒小于的最小值
显然,的最小值在时取得,且最小值为,故有
所以① 或②解①得,,不等式组②无解.
故,实数的取值范围是
4.解:(Ⅰ), ,
,
又数列成等比数列, ,所以 ;
又公比,所以 ;
又,, ;
数列构成一个首相为1公差为1的等差数列, ,
当, ;();
(Ⅱ)
;
由得,满足的最小正整数为112.
5.解:(Ⅰ) ∵当∈时,,,成等差数列,,,成等比数列.
∴2=+, =. 又∵,,∴≥0,≥0 , 且,∴(≥2),
∴数列﹛﹜是等差数列,又,∴,也适合.∴, .
(Ⅱ) 将,代入不等式≥ ()
整理得:≥0
令,则是关于的一次函数,
由题意可得 ∴ ,解得≤1或≥3.
∴存在最小自然数,使得当≥时,不等式()恒成立.
(Ⅲ) 由(1)得:…+.∴,(≥2),
∴
由()+()+…+()
…+)…+,
即:…+)…+
∵…+<…+
=…+
∴当都有
6.解:(Ⅰ)由 设
设: 又(1,0)关于 对称点
为(0,1)在上,所以1=0+b,b=1 所以:
(Ⅱ)因为 所以
(Ⅲ)所以
7.解:(Ⅰ)化简即
即 由a1=1,故数列{}
是以为首项,公比为2的等比数列。
故即
(Ⅱ)由已知得
故
8.解:(Ⅰ) 证:由题意,即,
∴,∴.∵常数且,∴为非零常数,
∴数列是以为首项,为公比的等比数列.
(Ⅱ)由(1)知,,
当时,. ∴, ①
. ②
②-①,得
∴ .
(Ⅲ)由(1)知,,要使对一切成立,
即对一切成立. ① 当时,,对一切恒成立;
② 当时,,对一切恒成立,只需,
∵单调递增,∴当时,. ∴,且, ∴.综上所述,存在实数满足条件.
9.解:(Ⅰ)当n≥3时,因①,
故②.②-①,得 bn-1-bn-2===1,为常数,
所以,数列{bn}为等差数列.因 b1==4,故 bn=n+3.
(Ⅱ) 因 ,故 .
所以 ,即 n<Sn<n+1.
10. 解:(Ⅰ)∵ ∴ 当时,,
∴ ,
∴ 当时,也满足上式, ∴数列的通项公式为
(Ⅱ)
,∴ 数列是单调递减数列,∴
11.解:(Ⅰ)由,得又,故 故数列为等比数列;
(Ⅱ)由(Ⅰ)可知 则
则对任意的恒成立
由不等式对恒成立,得
或
12.解:(Ⅰ)
是首项为的等比数列
当仍满足上式。
(Ⅱ)由(Ⅰ)得,当时,
两式作差得
(Ⅲ)
当时,,当时,
祝你成功
1.已知函数.
(Ⅰ)数列求数列的通项公式;
(Ⅱ)已知数列,求数列的通项公式;
(Ⅲ)设的前n项和为Sn,若不等式对所有的正整数n恒成立,求的取值范围。
2.已知数列中,,,记为的前项的和.
(Ⅰ)设,证明:数列是等比数列;(Ⅱ)求;
(Ⅲ)不等式对于一切恒成立,求实数的最大值.
3.已知数列的前五项依次是. 正数数列的前项和为,且.(Ⅰ)通过观察和归纳写出符合条件的数列的一个通项公式;
(Ⅱ)求的表达式;(Ⅲ)在(Ⅰ)、(Ⅱ)的条件下,,当时,设,是数列的前项和,且恒成立,求实数的取值范围.
4.已知点(1,)是函数且)的图象上一点,等比数列的前项和为,数列的首项为,且前项和满足-=+().(Ⅰ)求数列和的通项公式;
(Ⅱ)若数列{前项和为,问>的最小正整数是多少 .
5.已知:数列﹛﹜,﹛﹜中,=0,=1,且当时,,,成等差数列,,,成等比数列.(Ⅰ)求数列﹛﹜,﹛﹜的通项公式;
(Ⅱ)求最小自然数,使得当≥时,对任意实数,不等式≥恒成立; (Ⅲ)设 (∈),求证:当≥2都有>2.
6.直线过(1,0)点,且关于直线y=x对称的直线为,已知点在上,。当n≥2时,有
(Ⅰ)求的方程;(Ⅱ)求{ an}的通项公式;
(Ⅲ)设求数列{ bn}的前n项和Sn
7.已知数列{ an }的前n项和Sn满足,Sn=2an+(—1)n,n≥1。
(Ⅰ)求数列{ an }的通项公式;
(Ⅱ)求证:对任意整数m>4,有
8.已知函数(为常数,且),且数列是首项为4,公差为2的等差数列. (Ⅰ) 求证:数列是等比数列;(Ⅱ) 若,当时,求数列的前项和;(Ⅲ) 若,问是否存在实数,使得中的每一项恒小于它后面的项?若存在,求出的范围;若不存在,说明理由.
9.已知数列{an}满足:a1=a2=a3=2,an+1=a1a2…an-1(n≥3),记
(n≥3).
(Ⅰ)求证数列{bn}为等差数列,并求其通项公式;
(Ⅱ)设,数列{}的前n项和为Sn,求证:n
(Ⅰ)写出的值(只写结果)并求出数列的通项公式;
(Ⅱ)设, 求的最大值。
11. 已知正项数列满足,,令.
(Ⅰ) 求证:数列为等比数列;
(Ⅱ) 记为数列的前项和,是否存在实数,使得不等式对恒成立?若存在,求出实数的取值范围;若不存在,请说明理由.
12.设数列
(Ⅰ)求数列的通项公式;
(Ⅱ)设,求数列
(Ⅲ)设,,记,设数列的前项和为,求证:对任意正整数都有;
2012考前金题巧练(6)参答
1. 解:(Ⅰ),
(Ⅱ)由已知得,
∴又所以的公比为2的等比数列,∴。
(Ⅲ) , 上是增函数
又不等式对所有的正整数n恒成立,故的取值范围是
2.解:(Ⅰ)所以是以,公比为的等比数列. (Ⅱ)由(Ⅰ)知,,当时,;当时,,即
(3)由(2), 即得所以,因(当时等号成立),即所求的最大值.
3.解:(Ⅰ)可以看出: ,,,
,,归纳可得:
(Ⅱ)因为,,所以,解得,即
当时,,所以,
即所以,,,…,
累加,得…所以,当时,,即,当时,也满足上式,所以,对所有,
(Ⅲ)在(Ⅰ)、(Ⅱ)的条件下,,当时,,当时,;当时
,因恒成立,即恒小于的最小值
显然,的最小值在时取得,且最小值为,故有
所以① 或②解①得,,不等式组②无解.
故,实数的取值范围是
4.解:(Ⅰ), ,
,
又数列成等比数列, ,所以 ;
又公比,所以 ;
又,, ;
数列构成一个首相为1公差为1的等差数列, ,
当, ;();
(Ⅱ)
;
由得,满足的最小正整数为112.
5.解:(Ⅰ) ∵当∈时,,,成等差数列,,,成等比数列.
∴2=+, =. 又∵,,∴≥0,≥0 , 且,∴(≥2),
∴数列﹛﹜是等差数列,又,∴,也适合.∴, .
(Ⅱ) 将,代入不等式≥ ()
整理得:≥0
令,则是关于的一次函数,
由题意可得 ∴ ,解得≤1或≥3.
∴存在最小自然数,使得当≥时,不等式()恒成立.
(Ⅲ) 由(1)得:…+.∴,(≥2),
∴
由()+()+…+()
…+)…+,
即:…+)…+
∵…+<…+
=…+
∴当都有
6.解:(Ⅰ)由 设
设: 又(1,0)关于 对称点
为(0,1)在上,所以1=0+b,b=1 所以:
(Ⅱ)因为 所以
(Ⅲ)所以
7.解:(Ⅰ)化简即
即 由a1=1,故数列{}
是以为首项,公比为2的等比数列。
故即
(Ⅱ)由已知得
故
8.解:(Ⅰ) 证:由题意,即,
∴,∴.∵常数且,∴为非零常数,
∴数列是以为首项,为公比的等比数列.
(Ⅱ)由(1)知,,
当时,. ∴, ①
. ②
②-①,得
∴ .
(Ⅲ)由(1)知,,要使对一切成立,
即对一切成立. ① 当时,,对一切恒成立;
② 当时,,对一切恒成立,只需,
∵单调递增,∴当时,. ∴,且, ∴.综上所述,存在实数满足条件.
9.解:(Ⅰ)当n≥3时,因①,
故②.②-①,得 bn-1-bn-2===1,为常数,
所以,数列{bn}为等差数列.因 b1==4,故 bn=n+3.
(Ⅱ) 因 ,故 .
所以 ,即 n<Sn<n+1.
10. 解:(Ⅰ)∵ ∴ 当时,,
∴ ,
∴ 当时,也满足上式, ∴数列的通项公式为
(Ⅱ)
,∴ 数列是单调递减数列,∴
11.解:(Ⅰ)由,得又,故 故数列为等比数列;
(Ⅱ)由(Ⅰ)可知 则
则对任意的恒成立
由不等式对恒成立,得
或
12.解:(Ⅰ)
是首项为的等比数列
当仍满足上式。
(Ⅱ)由(Ⅰ)得,当时,
两式作差得
(Ⅲ)
当时,,当时,
同课章节目录
