5.1.1相交线 课件(共18张PPT)
图片预览






文档简介
(共19张PPT)
5.1相交线
人教版
七年级下册
新知导入
新知导入
观察下面的图片,说一说图中直线与直线之间的位置关系。
新知导入
新知导入
观察下面的图片,说一说图中直线与直线之间的位置关系。
新知导入
观察剪刀剪开布片过程中有关角的变化.
可以发现,握紧剪刀的把手时,随着两个把手之间的角逐渐变小,剪刀刃之间的角也相应变小,直到剪开布片.
新知导入
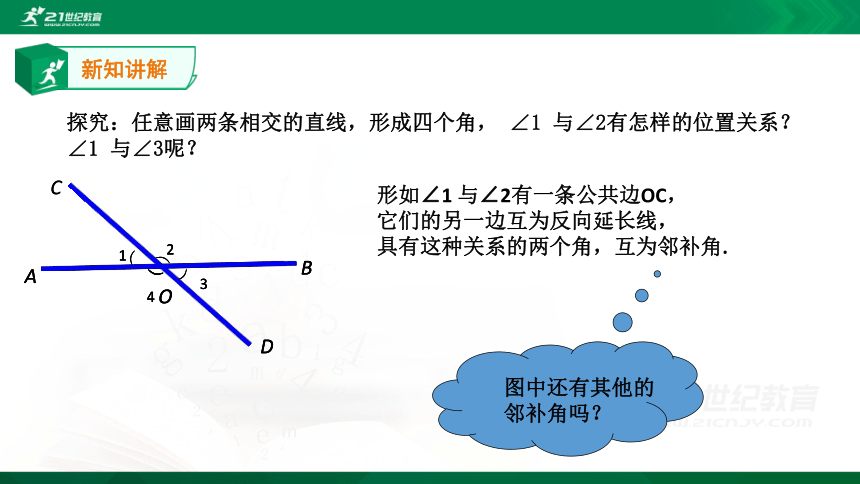
探究:任意画两条相交的直线,形成四个角,
∠1
与∠2有怎样的位置关系?
∠1
与∠3呢?
新知讲解
O
A
B
C
︶
︵
︵
︵
1
2
3
4
形如∠1
与∠2有一条公共边OC,
它们的另一边互为反向延长线,
具有这种关系的两个角,互为邻补角.
D
图中还有其他的
邻补角吗?
O
A
B
︶
︵
︵
︵
1
2
3
4
D
C
O
A
B
︶
︵
︵
︵
1
2
3
4
D
探究:任意画两条相交的直线,形成四个角,
∠1
与∠2有怎样的位置关系?
∠1
与∠3呢?
新知讲解
O
A
B
C
︶
︵
︵
︵
1
2
3
4
D
形如∠1
与∠3有一个公共顶点O,
并且∠1
的两边分别是∠3的两边的反向延长线,
具有这种位置关系的两个角,互为对顶角.
图中还有其他的
对顶角吗?
探究:分别量一下各个角的度数,∠1和∠2的度数有什么关系?
∠1和∠3呢?
新知讲解
C
O
A
B
︶
︵
︵
︵
1
2
3
4
D
∠1+∠2=180
°
∠1=∠3
在图中,∠1与∠2互补,∠2和∠3互补,
由同角的补角相等,可知∠1=∠3,
类似的∠2=∠4.
所以,我们得到对顶角的性质:
对顶角相等.
推导过程可以写:
因为
∠1与∠2互补,∠2和∠3互补(邻补角的定义),
所以
∠1=∠3(同角的补角相等).
新知讲解
例1:如图,直线a,b相交于点O,∠1=400,求∠2
,∠3
,
∠4
的度数.
解:由邻补角定义,可得
∠2=180°-∠1
=180°-
40°=
140°
由对顶角相等,可得
∠1=∠3=40°;
∠2=∠4=140°.
1
2
3
4
a
b
课堂练习
1.如图,∠1和∠2是对顶角的是(
)
︵
︵
1
2
︵
︵
1
2
︵
︵
1
2
︵
︵
1
2
A
B
C
D
A
课堂练习
2.如图,O是直线AB上一点,若∠1=37°,则∠AOC的度数是(
)
A.113°
B.
37°
C.143°
D.37°或143°
1
︵
A
O
C
B
C
课堂练习
3.下列说法正确的是(
)
A.
大小相等的两个角互为对顶角
B.
有公共顶点且相等的两个角是对顶角
C.
如果两个角的和为180°,则这两个角互为邻补角
D.
—个角的邻补角可能是锐角、钝角或直角
D
课堂练习
4.如图,两直线相交于一点,若∠1+∠3=100°,则∠2=(
)
C
O
A
B
︶
︵
︵
︵
1
2
3
4
D
A.100°
B.
80°
C.120°
D.130°
D
5.如图,直线AB,CD相交于点O,∠2-∠1=15°,∠3=130°.
(1)求∠2的度数;
(2)试说明OE平分∠COB.
课堂练习
解:(1)因为∠1+∠3=180°,∠3=130°,
所以∠1=180°-∠3=50°.
因为∠2-∠1=15°,所以∠2=15°+∠1=65°.
(2)因为∠1+∠COE+∠2=180°,∠1=50°,∠2=65°,
所以∠COE=65°.
所以∠COE=∠2.
所以OE平分∠COB.
课堂总结
1、邻补角定义:
有一条公共边,它们的另一边互为反向延长线,具有这种关系的两个角,互为邻补角.
2.对顶角定义:
有一个公共顶点,并且一个角的两边分别是别一个角两边的反向延长线,
具有这种位置关系的两个角,互为对顶角.
3.邻补角、对顶角的性质:
邻补角互补,对顶角相等.
板书设计
5.1相交线
一、邻补角定义
二、对顶角定义
三、对顶角和邻补角性质
教师板演区
学生展示区
作业布置
基础作业
教材第7页习题5.1第1、2题
能力作业
教材第8页习题5.1第8题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
5.1相交线
人教版
七年级下册
新知导入
新知导入
观察下面的图片,说一说图中直线与直线之间的位置关系。
新知导入
新知导入
观察下面的图片,说一说图中直线与直线之间的位置关系。
新知导入
观察剪刀剪开布片过程中有关角的变化.
可以发现,握紧剪刀的把手时,随着两个把手之间的角逐渐变小,剪刀刃之间的角也相应变小,直到剪开布片.
新知导入
探究:任意画两条相交的直线,形成四个角,
∠1
与∠2有怎样的位置关系?
∠1
与∠3呢?
新知讲解
O
A
B
C
︶
︵
︵
︵
1
2
3
4
形如∠1
与∠2有一条公共边OC,
它们的另一边互为反向延长线,
具有这种关系的两个角,互为邻补角.
D
图中还有其他的
邻补角吗?
O
A
B
︶
︵
︵
︵
1
2
3
4
D
C
O
A
B
︶
︵
︵
︵
1
2
3
4
D
探究:任意画两条相交的直线,形成四个角,
∠1
与∠2有怎样的位置关系?
∠1
与∠3呢?
新知讲解
O
A
B
C
︶
︵
︵
︵
1
2
3
4
D
形如∠1
与∠3有一个公共顶点O,
并且∠1
的两边分别是∠3的两边的反向延长线,
具有这种位置关系的两个角,互为对顶角.
图中还有其他的
对顶角吗?
探究:分别量一下各个角的度数,∠1和∠2的度数有什么关系?
∠1和∠3呢?
新知讲解
C
O
A
B
︶
︵
︵
︵
1
2
3
4
D
∠1+∠2=180
°
∠1=∠3
在图中,∠1与∠2互补,∠2和∠3互补,
由同角的补角相等,可知∠1=∠3,
类似的∠2=∠4.
所以,我们得到对顶角的性质:
对顶角相等.
推导过程可以写:
因为
∠1与∠2互补,∠2和∠3互补(邻补角的定义),
所以
∠1=∠3(同角的补角相等).
新知讲解
例1:如图,直线a,b相交于点O,∠1=400,求∠2
,∠3
,
∠4
的度数.
解:由邻补角定义,可得
∠2=180°-∠1
=180°-
40°=
140°
由对顶角相等,可得
∠1=∠3=40°;
∠2=∠4=140°.
1
2
3
4
a
b
课堂练习
1.如图,∠1和∠2是对顶角的是(
)
︵
︵
1
2
︵
︵
1
2
︵
︵
1
2
︵
︵
1
2
A
B
C
D
A
课堂练习
2.如图,O是直线AB上一点,若∠1=37°,则∠AOC的度数是(
)
A.113°
B.
37°
C.143°
D.37°或143°
1
︵
A
O
C
B
C
课堂练习
3.下列说法正确的是(
)
A.
大小相等的两个角互为对顶角
B.
有公共顶点且相等的两个角是对顶角
C.
如果两个角的和为180°,则这两个角互为邻补角
D.
—个角的邻补角可能是锐角、钝角或直角
D
课堂练习
4.如图,两直线相交于一点,若∠1+∠3=100°,则∠2=(
)
C
O
A
B
︶
︵
︵
︵
1
2
3
4
D
A.100°
B.
80°
C.120°
D.130°
D
5.如图,直线AB,CD相交于点O,∠2-∠1=15°,∠3=130°.
(1)求∠2的度数;
(2)试说明OE平分∠COB.
课堂练习
解:(1)因为∠1+∠3=180°,∠3=130°,
所以∠1=180°-∠3=50°.
因为∠2-∠1=15°,所以∠2=15°+∠1=65°.
(2)因为∠1+∠COE+∠2=180°,∠1=50°,∠2=65°,
所以∠COE=65°.
所以∠COE=∠2.
所以OE平分∠COB.
课堂总结
1、邻补角定义:
有一条公共边,它们的另一边互为反向延长线,具有这种关系的两个角,互为邻补角.
2.对顶角定义:
有一个公共顶点,并且一个角的两边分别是别一个角两边的反向延长线,
具有这种位置关系的两个角,互为对顶角.
3.邻补角、对顶角的性质:
邻补角互补,对顶角相等.
板书设计
5.1相交线
一、邻补角定义
二、对顶角定义
三、对顶角和邻补角性质
教师板演区
学生展示区
作业布置
基础作业
教材第7页习题5.1第1、2题
能力作业
教材第8页习题5.1第8题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
