广东省佛山市三水区2012届高三5月考前金题巧练理科数学(2)
文档属性
| 名称 | 广东省佛山市三水区2012届高三5月考前金题巧练理科数学(2) |  | |
| 格式 | zip | ||
| 文件大小 | 515.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-05-24 12:26:51 | ||
图片预览




文档简介
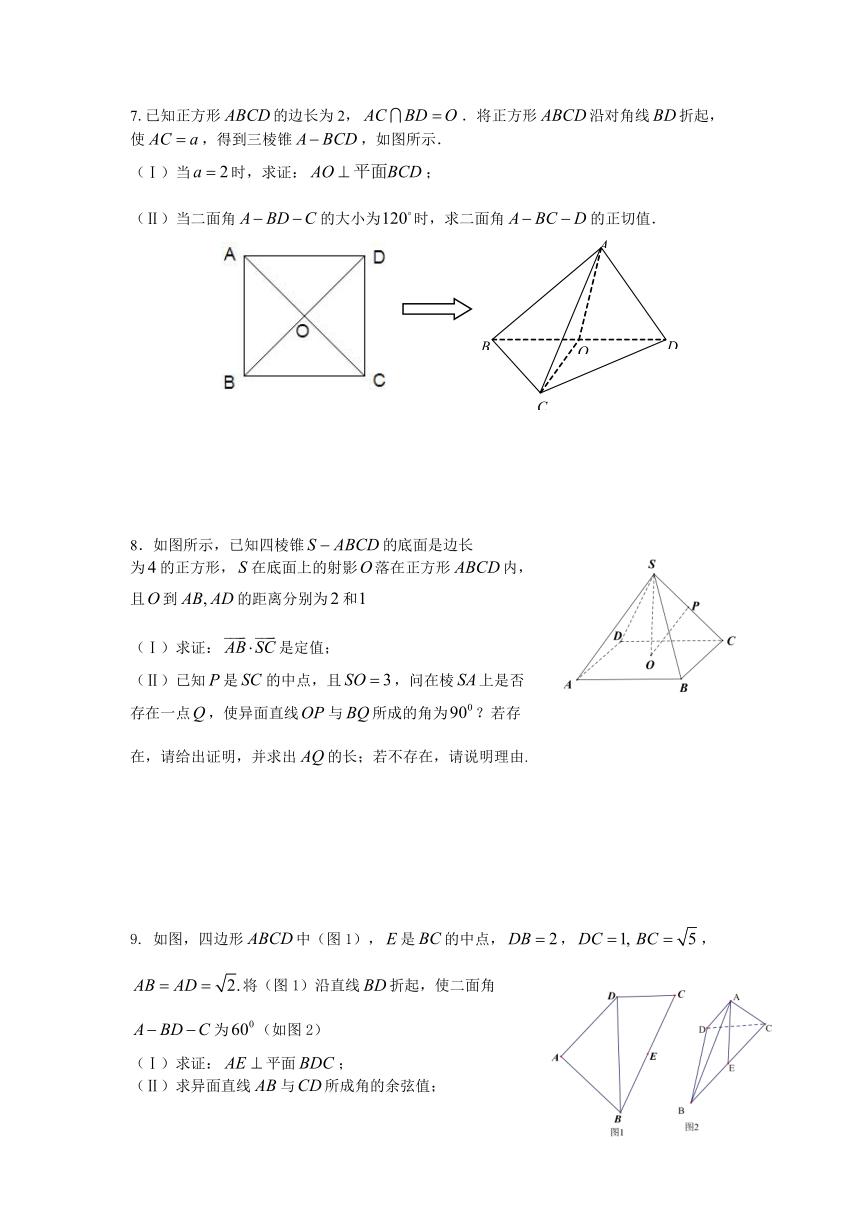
2012考前金题巧练(2)
祝你成功
1.已知斜三棱柱的底面是直角三角形,,侧棱与底面所成角为,点在底面上射影D落在BC上.
(Ⅰ)求证:平面;
(Ⅱ)若点D恰为BC中点,且,求的大小;
(III)若,且当时,求二面角的大小.
2.如图4,已知平面是圆柱的轴截面(经过圆柱的轴的截面),BC是圆柱底面的直径,O为底面圆心,E为母线的中点,已知
(Ⅰ)求证:⊥平面;(Ⅱ)求二面角的余弦值;
(III)求三棱锥的体积.
3.在四棱锥中,侧面底面,,为中点,底面是直角梯形。
(Ⅰ)求证:平面;(Ⅱ)求证:平面;
(III)设为侧棱上一点,;
试确定的值,使得二面角为为.
4.如图,已知正方形和矩形所在的平面互相垂直,
,是线段的中点.
(Ⅰ)求证//平面;(Ⅱ)求二面角的大小;
(Ⅲ)试在线段上确定一点,使得与所成的角是60.
5.在四棱锥中,底面是直角梯形,∥,,,平面平面.
(Ⅰ)求证:平面;
(Ⅱ)求平面和平面所成二面角(小于)的大小;
(Ⅲ)在棱上是否存在点使得∥平面?若存在,求的值;若不存在,请说明理由.
6. 如图,在四棱锥中,底面为菱形,,为的中点,.
(Ⅰ)求证:平面;
(Ⅱ)点在线段上,,试确定的值,
使平面;
(Ⅲ)若平面,平面平面, 求二面角的大小.
7.已知正方形的边长为2,.将正方形沿对角线折起,使,得到三棱锥,如图所示.
(Ⅰ)当时,求证:;
(Ⅱ)当二面角的大小为时,求二面角的正切值.
8.如图所示,已知四棱锥的底面是边长
为的正方形,在底面上的射影落在正方形内,
且到的距离分别为和
(Ⅰ)求证:是定值;
(Ⅱ)已知是的中点,且,问在棱上是否
存在一点,使异面直线与所成的角为?若存
在,请给出证明,并求出的长;若不存在,请说明理由.
9. 如图,四边形中(图1),是的中点,,,将(图1)沿直线折起,使二面角为(如图2)
(Ⅰ)求证:平面;
(Ⅱ)求异面直线与所成角的余弦值;
(Ⅲ)求点到平面的距离.
10.如图,在三棱锥中,为的中点,平面⊥平面, ,.
(Ⅰ)求证:;
(Ⅱ)求直线与平面所成角的正弦值;
(III)若动点M在底面三角形ABC上,二面角的余弦值为,求BM的最小值.
2012考前金题巧练(2)参答
1.解:(I)∵B1D⊥平面ABC,AC平面ABC,∴
又∵,,∴AC⊥平面
(II)
∴四边形为菱形, 又∵D为BC的中点,∴为侧棱和底面所成的角,
∴∴,即侧棱与底面所成角.
(III)以C为原点,CA为x轴CB为y轴,过C点且垂直于平面ABC的直线为Z轴,建立空间直角坐标系,
则A(a,0,0),B(0,a,0),,平面ABC的法向量,设平面ABC1的法向量为,由,即, ,∴二面角的大小为
2.解:依题意可知, 平面ABC,∠=90°,
空间向量法 如图建立空间直角坐标系,因为=4,
则
(Ⅰ),
,∴,∴
, ∴,∴,∵ 平面 ∴ ⊥平面
(Ⅱ) 平面AEO的法向量为,设平面 B1AE的法向量为
, 即
令x=2,则
∴
∴二面角B1—AE—F的余弦值为
(III)因为,∴, ∴
∵,
∴
3.解:(Ⅰ)取的中点,连结,因为为中点,所以,且。在梯形中,,所以四边形为平行四边形,所以平面,平面,所以平面
(Ⅱ)平面平面,,所以平面,所以
如图,以D为原点建立空间直角坐标系,则,
,又由平面,
可得,又,所以平面
(III)平面的法向量为,,,设平面的法向量为,,,由得
4解:(Ⅰ)建立如图所示的空间直角坐标系.
设,连接NE, 则点N、E的坐标分别是(、(0,0,1),
∴, 又点A、M的坐标分别是,(
∴ =(∴且NE与AM不共线,∴NE∥AM.又∵平面BDE, 平面BDE,∴AM∥平面BDF.
(Ⅱ)∵AF⊥AB,AB⊥AD,AF∴AB⊥平面ADF.
∴为平面DAF的法向量.
∵=(·=0,
∴=(·=0得
,,∴NE为平面BDF的法向量.
∴cos<=∴AB与NE的夹角是60 .即所求二面角A—DF—B的大小是60 .
(Ⅲ)设P(t,t,0)(0≤t≤)得∴=(,0,0)
又∵PF和BC所成的角是60 .∴
解得或(舍去),即点P是AC的中点.
5.(Ⅰ)证明:因为 ,所以 . 因为 平面平面,平面平面, 平面,所以 平面.
(Ⅱ)解:取的中点,连接,因为,所以 .
因为 平面平面,平面平面,平面,
所以 平面. 如图,以为原点,所在的直线为轴,在平面内过垂直于的直
线为轴,所在的直线为轴建立空间直角坐标系.不妨设.由
直角梯形中可得,,
.所以 ,.设平面的法向量.因为 所以 即令,则.所以 . 取平面的一个法向量n.所以 .所以 平面和平面所成的二面角(小于)的大小为.
(Ⅲ)解:在棱上存在点使得∥平面,此时. 理由如下:
取的中点,连接,,.则 ∥,.
因为 ,所以 .因为 ∥,所以 四边形是平行四边形.所以 ∥.因为 ,所以 平面∥平面. 因为 平面,所以 ∥平面.
6. 证明:(Ⅰ)连接 。因为四边形为菱形,,
所以△为正三角形.又为中点,所以.
因为,为的中点,所以.
又,所以平面.
(Ⅱ)当时,∥平面.下面证明:
连接交于,连接. 因为∥, 所以. 因为∥平面,平面,平面平面,所以∥.所以.所以,即. 因为,所以.所以, 所以∥.又平面,平面,所以∥平面.
(Ⅲ)因为, 又平面平面,交线为,
所以平面. 以为坐标原点,分别以所在的直线为轴, 建立如图所示的空间直角坐标系.由===2,则有,,.设平面的法向量为=,由,且,,可得令得.
所以=为的一个法向量,取平面的法向量=,
则, 故二面角的大小为60
7. (Ⅰ)证明:根据题意,在中,,,所以,所以.因为是正方形的对角线,所以.因为,所以.
(Ⅱ)解:由(1)知,,如图,以为原点,,所在的直线分别为轴,轴建立如图的空间直角坐标系,则有,,,.设,则,.又设面的法向量为,
则即 所以,令,则.
所以.因为平面的一个法向量为,
且二面角的大小为,所以,得.
因为,所以.解得.所以.设平面的法向量为,因为,则,即令,则.
所以.设二面角的平面角为,所以.所以.
所以二面角的正切值为.
8.解:(Ⅰ)证明:在内,作交于,连接,平面,平面,, ,,为定值。
(Ⅱ)解:以O为坐标原点,以OS所在直线为轴,以过O且平行于的直线为轴,以过点O且平行于的直线为轴,建立如图所示直角坐标系,于是
设点,则存在使,
即,得,即令,得
由,知点在棱上,且,
9.解:(Ⅰ) 因 , 满足:, ,
如图,以D为原点DB为x轴,DC为y轴,建立空间直角坐标系, 则条件可知D(0,0,0), B(2,0,0),C(0,1,0),, A(a,b,c) (由图知a>0,b>0,c>0)得,平面BCD的法向量可取,
,所以平面ABD的一个法向量为 则锐二面角的余弦值
从而有,
所以平面
(Ⅱ)由(1),D(0,0,0), B(2,0,0),C(0,1,0),
设异面直线与所成角为,则
(Ⅲ)由可知满足,
是平面ACD的一个法向量,
记点到平面的距离d,则在法向量方向上的投影绝对值为d
则 所以d
10.解:(Ⅰ)因为为的中点, AB=BC,所以,∵平面⊥平面,平面平面,∴平面PAC,∴;
(Ⅱ)以为坐标原点,分别为轴
建立如图所示空间直角坐标系,因为AB=BC=PA=,所以OB=OC=OP=1,从而O(0,0,0),B(1,0,0),A(0,-1,0),C(0,1,0),P(0,0,1),
∴
设平面PBC的法向量,由,得方程组,取,
∴∴直线PA与平面PBC所成角的正弦值为;
(III)由题意平面PAC的法向量, 设平面PAM的法向量为∵又因为,∴ 取,
∴=
∴,∴ 或 (舍去)
∴B点到AM的最小值为垂直距离.
A
B
C
D
O
A
B
C
D
O
y
x
z
祝你成功
1.已知斜三棱柱的底面是直角三角形,,侧棱与底面所成角为,点在底面上射影D落在BC上.
(Ⅰ)求证:平面;
(Ⅱ)若点D恰为BC中点,且,求的大小;
(III)若,且当时,求二面角的大小.
2.如图4,已知平面是圆柱的轴截面(经过圆柱的轴的截面),BC是圆柱底面的直径,O为底面圆心,E为母线的中点,已知
(Ⅰ)求证:⊥平面;(Ⅱ)求二面角的余弦值;
(III)求三棱锥的体积.
3.在四棱锥中,侧面底面,,为中点,底面是直角梯形。
(Ⅰ)求证:平面;(Ⅱ)求证:平面;
(III)设为侧棱上一点,;
试确定的值,使得二面角为为.
4.如图,已知正方形和矩形所在的平面互相垂直,
,是线段的中点.
(Ⅰ)求证//平面;(Ⅱ)求二面角的大小;
(Ⅲ)试在线段上确定一点,使得与所成的角是60.
5.在四棱锥中,底面是直角梯形,∥,,,平面平面.
(Ⅰ)求证:平面;
(Ⅱ)求平面和平面所成二面角(小于)的大小;
(Ⅲ)在棱上是否存在点使得∥平面?若存在,求的值;若不存在,请说明理由.
6. 如图,在四棱锥中,底面为菱形,,为的中点,.
(Ⅰ)求证:平面;
(Ⅱ)点在线段上,,试确定的值,
使平面;
(Ⅲ)若平面,平面平面, 求二面角的大小.
7.已知正方形的边长为2,.将正方形沿对角线折起,使,得到三棱锥,如图所示.
(Ⅰ)当时,求证:;
(Ⅱ)当二面角的大小为时,求二面角的正切值.
8.如图所示,已知四棱锥的底面是边长
为的正方形,在底面上的射影落在正方形内,
且到的距离分别为和
(Ⅰ)求证:是定值;
(Ⅱ)已知是的中点,且,问在棱上是否
存在一点,使异面直线与所成的角为?若存
在,请给出证明,并求出的长;若不存在,请说明理由.
9. 如图,四边形中(图1),是的中点,,,将(图1)沿直线折起,使二面角为(如图2)
(Ⅰ)求证:平面;
(Ⅱ)求异面直线与所成角的余弦值;
(Ⅲ)求点到平面的距离.
10.如图,在三棱锥中,为的中点,平面⊥平面, ,.
(Ⅰ)求证:;
(Ⅱ)求直线与平面所成角的正弦值;
(III)若动点M在底面三角形ABC上,二面角的余弦值为,求BM的最小值.
2012考前金题巧练(2)参答
1.解:(I)∵B1D⊥平面ABC,AC平面ABC,∴
又∵,,∴AC⊥平面
(II)
∴四边形为菱形, 又∵D为BC的中点,∴为侧棱和底面所成的角,
∴∴,即侧棱与底面所成角.
(III)以C为原点,CA为x轴CB为y轴,过C点且垂直于平面ABC的直线为Z轴,建立空间直角坐标系,
则A(a,0,0),B(0,a,0),,平面ABC的法向量,设平面ABC1的法向量为,由,即, ,∴二面角的大小为
2.解:依题意可知, 平面ABC,∠=90°,
空间向量法 如图建立空间直角坐标系,因为=4,
则
(Ⅰ),
,∴,∴
, ∴,∴,∵ 平面 ∴ ⊥平面
(Ⅱ) 平面AEO的法向量为,设平面 B1AE的法向量为
, 即
令x=2,则
∴
∴二面角B1—AE—F的余弦值为
(III)因为,∴, ∴
∵,
∴
3.解:(Ⅰ)取的中点,连结,因为为中点,所以,且。在梯形中,,所以四边形为平行四边形,所以平面,平面,所以平面
(Ⅱ)平面平面,,所以平面,所以
如图,以D为原点建立空间直角坐标系,则,
,又由平面,
可得,又,所以平面
(III)平面的法向量为,,,设平面的法向量为,,,由得
4解:(Ⅰ)建立如图所示的空间直角坐标系.
设,连接NE, 则点N、E的坐标分别是(、(0,0,1),
∴, 又点A、M的坐标分别是,(
∴ =(∴且NE与AM不共线,∴NE∥AM.又∵平面BDE, 平面BDE,∴AM∥平面BDF.
(Ⅱ)∵AF⊥AB,AB⊥AD,AF∴AB⊥平面ADF.
∴为平面DAF的法向量.
∵=(·=0,
∴=(·=0得
,,∴NE为平面BDF的法向量.
∴cos<=∴AB与NE的夹角是60 .即所求二面角A—DF—B的大小是60 .
(Ⅲ)设P(t,t,0)(0≤t≤)得∴=(,0,0)
又∵PF和BC所成的角是60 .∴
解得或(舍去),即点P是AC的中点.
5.(Ⅰ)证明:因为 ,所以 . 因为 平面平面,平面平面, 平面,所以 平面.
(Ⅱ)解:取的中点,连接,因为,所以 .
因为 平面平面,平面平面,平面,
所以 平面. 如图,以为原点,所在的直线为轴,在平面内过垂直于的直
线为轴,所在的直线为轴建立空间直角坐标系.不妨设.由
直角梯形中可得,,
.所以 ,.设平面的法向量.因为 所以 即令,则.所以 . 取平面的一个法向量n.所以 .所以 平面和平面所成的二面角(小于)的大小为.
(Ⅲ)解:在棱上存在点使得∥平面,此时. 理由如下:
取的中点,连接,,.则 ∥,.
因为 ,所以 .因为 ∥,所以 四边形是平行四边形.所以 ∥.因为 ,所以 平面∥平面. 因为 平面,所以 ∥平面.
6. 证明:(Ⅰ)连接 。因为四边形为菱形,,
所以△为正三角形.又为中点,所以.
因为,为的中点,所以.
又,所以平面.
(Ⅱ)当时,∥平面.下面证明:
连接交于,连接. 因为∥, 所以. 因为∥平面,平面,平面平面,所以∥.所以.所以,即. 因为,所以.所以, 所以∥.又平面,平面,所以∥平面.
(Ⅲ)因为, 又平面平面,交线为,
所以平面. 以为坐标原点,分别以所在的直线为轴, 建立如图所示的空间直角坐标系.由===2,则有,,.设平面的法向量为=,由,且,,可得令得.
所以=为的一个法向量,取平面的法向量=,
则, 故二面角的大小为60
7. (Ⅰ)证明:根据题意,在中,,,所以,所以.因为是正方形的对角线,所以.因为,所以.
(Ⅱ)解:由(1)知,,如图,以为原点,,所在的直线分别为轴,轴建立如图的空间直角坐标系,则有,,,.设,则,.又设面的法向量为,
则即 所以,令,则.
所以.因为平面的一个法向量为,
且二面角的大小为,所以,得.
因为,所以.解得.所以.设平面的法向量为,因为,则,即令,则.
所以.设二面角的平面角为,所以.所以.
所以二面角的正切值为.
8.解:(Ⅰ)证明:在内,作交于,连接,平面,平面,, ,,为定值。
(Ⅱ)解:以O为坐标原点,以OS所在直线为轴,以过O且平行于的直线为轴,以过点O且平行于的直线为轴,建立如图所示直角坐标系,于是
设点,则存在使,
即,得,即令,得
由,知点在棱上,且,
9.解:(Ⅰ) 因 , 满足:, ,
如图,以D为原点DB为x轴,DC为y轴,建立空间直角坐标系, 则条件可知D(0,0,0), B(2,0,0),C(0,1,0),, A(a,b,c) (由图知a>0,b>0,c>0)得,平面BCD的法向量可取,
,所以平面ABD的一个法向量为 则锐二面角的余弦值
从而有,
所以平面
(Ⅱ)由(1),D(0,0,0), B(2,0,0),C(0,1,0),
设异面直线与所成角为,则
(Ⅲ)由可知满足,
是平面ACD的一个法向量,
记点到平面的距离d,则在法向量方向上的投影绝对值为d
则 所以d
10.解:(Ⅰ)因为为的中点, AB=BC,所以,∵平面⊥平面,平面平面,∴平面PAC,∴;
(Ⅱ)以为坐标原点,分别为轴
建立如图所示空间直角坐标系,因为AB=BC=PA=,所以OB=OC=OP=1,从而O(0,0,0),B(1,0,0),A(0,-1,0),C(0,1,0),P(0,0,1),
∴
设平面PBC的法向量,由,得方程组,取,
∴∴直线PA与平面PBC所成角的正弦值为;
(III)由题意平面PAC的法向量, 设平面PAM的法向量为∵又因为,∴ 取,
∴=
∴,∴ 或 (舍去)
∴B点到AM的最小值为垂直距离.
A
B
C
D
O
A
B
C
D
O
y
x
z
同课章节目录
