广东省佛山市三水区2012届高三5月考前金题巧练理科数学(1)
文档属性
| 名称 | 广东省佛山市三水区2012届高三5月考前金题巧练理科数学(1) |  | |
| 格式 | zip | ||
| 文件大小 | 568.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-05-24 12:28:10 | ||
图片预览



文档简介
2012考前金题巧练(1)
祝你成功
1.如图,在棱长为1的正方体中,是侧棱上的一点,.
(Ⅰ)试确定,使得直线与平面所成角的正切值为;
(Ⅱ)在线段上是否存在一个定点,使得对任意的,在平面上的射影垂直于,并证明你的结论.
2.如图,在三棱锥V-ABC中,VC⊥底面ABC,AC⊥BC,D是AB的中点,且AC=BC=a,∠VDC=θ。(Ⅰ)求证:平面VAB⊥平面VCD ;
(Ⅱ)当角θ变化时,求直线BC与平面VAB所成的角的取值范围;
3.如图,棱柱中,都与平面所成的角相等,
∠CAB=90°,AC=AB=A1B=a,D为BC上的点,且A1C//平面ADB1。求:
(Ⅰ)A1C与平面ADB1的距离;(Ⅱ)二面角A1—AB—C的大小;
(Ⅲ)AB1与平面ABC所成的角的大小。
4.在四棱锥中,底面是菱形,.
(Ⅰ)若,求证:平面;
(Ⅱ)若平面平面,求证:;
(Ⅲ)在棱上是否存在点(异于点)使得∥平面,若存在,求的值;若不存在,说明理由.
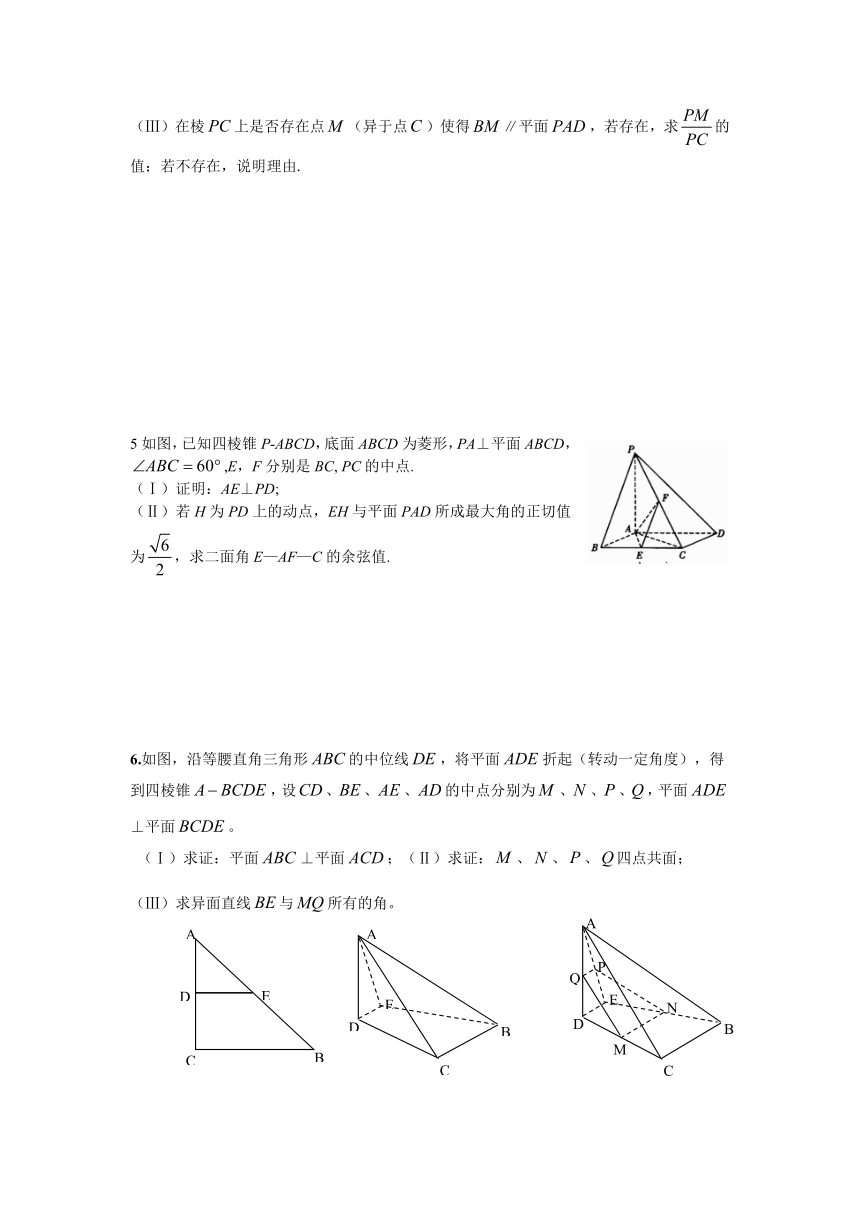
5如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,,E,F分别是BC, PC的中点.
(Ⅰ)证明:AE⊥PD;
(Ⅱ)若H为PD上的动点,EH与平面PAD所成最大角的正切值为,求二面角E—AF—C的余弦值.
6.如图,沿等腰直角三角形的中位线,将平面折起(转动一定角度),得到四棱锥,设、、、的中点分别为、、、,平面⊥平面。
(Ⅰ)求证:平面⊥平面;(Ⅱ)求证:、、、四点共面;
(Ⅲ)求异面直线与所有的角。
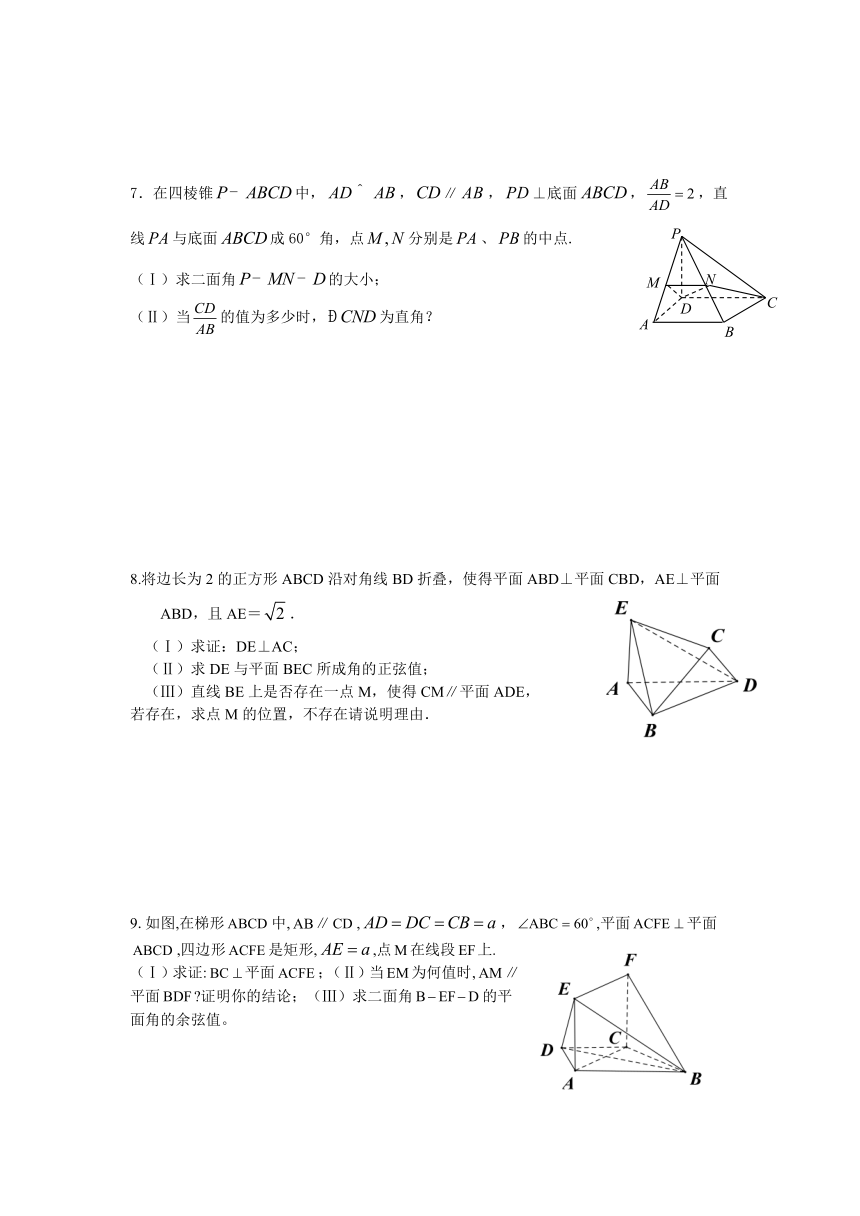
7.在四棱锥中,,∥,⊥底面,,直线与底面成60°角,点分别是、的中点.
(Ⅰ)求二面角的大小;
(Ⅱ)当的值为多少时,为直角?
8.将边长为2的正方形ABCD沿对角线BD折叠,使得平面ABD⊥平面CBD,AE⊥平面ABD,且AE=.
(Ⅰ)求证:DE⊥AC;
(Ⅱ)求DE与平面BEC所成角的正弦值;
(Ⅲ)直线BE上是否存在一点M,使得CM∥平面ADE,
若存在,求点M的位置,不存在请说明理由.
9.如图,在梯形中,∥,,,平面平面,四边形是矩形,,点在线段上.
(Ⅰ)求证:平面;(Ⅱ)当为何值时,∥平面 证明你的结论;(Ⅲ)求二面角的平面角的余弦值。
10.已知梯形ABCD中,AD∥BC,∠ABC =∠BAD =,AB=BC=2AD=4,E、F分别是AB、CD上的点,EF∥BC,AE = x,G是BC的中点.沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF (如图).
(Ⅰ)当x=2时,求证:BD⊥EG ;
(Ⅱ)若以F、B、C、D为顶点的三棱锥的体积记为,求的最大值;
(Ⅲ)当取得最大值时,求二面角D-BF-C的余弦值.
2012考前金题巧练(1)参答
1.解:(Ⅰ)建立如图所示的空间直角坐标系,则A(1,0,0),B(1,1,0),P(0,1,m),C(0,1,0),D(0,0,0),B1(1,1,1),D1(0,0,1)所以又由知,为平面的一个法向量。设AP与平面所成的角为,则。依题意有解得。故当时,
直线AP与平面所成的角的正切值为。
(Ⅱ)若在A1C1上存在这样的点Q,设此点的横坐标为,则Q(x,1-,1),。依题意,对任意的m要使D1Q在平面APD1上的射影垂直于AP,等价于D1Q⊥AP即Q为A1C1的中点时,满足题设要求。
2.解:(Ⅰ)以所在的直线分别为轴、轴、轴,建立如图所示的空间直角坐标系,则,
于是,,,.
从而,即.
同理,
即.又,平面.
又平面.平面平面.
(Ⅱ)设直线与平面所成的角为,平面的一个法向量为,
则由.得
可取,又,
于是,
,,.又,.
即直线与平面所成角的取值范围为.
3.解:建立如图坐标系,则A(0,0,0)B(a,0,0),C(0,a,0)
连A1B,由条件知,△A1AB和△A1AC均为等边△且边长为a,
∴∠A1AB=∠A1AC=60°,设A(x,y,z),则
由
同理得
(I)A1C//面ADB1,∵A1C//ED,又E为A1B中点,∴D为BC中点,
∴D,设面ADB1的法向量
则取
设A1C面ADB1的距离为d,则
(Ⅱ)平面ABC的一个法向量为,设平面A1AB的法向量为
则,取
设,则
即二面角A1—AB—C的大小为
(Ⅲ)设AB1与平面ABC所成角为θ2,则
,即AB1与平面ABC所成角为
4.(Ⅰ)证明:因为 底面是菱形
所以 . 因为 ,,
所以 平面.
(Ⅱ)证明:由(Ⅰ)可知.
因为 平面平面,平面平面,平面,所以 平面. 因为 平面,
所以 . 因为 底面是菱形,所以 .所以 .
(Ⅲ)解:不存在. 下面用反证法说明. 假设存在点(异于点)使得∥平面.
在菱形中,∥,因为 平面,平面,所以 ∥平面. 因为 平面,平面,,所以 平面∥平面.而平面与平面相交,矛盾.
5(Ⅰ)证明:由四边形ABCD为菱形,∠ABC=60°,可得△ABC为正三角形.
因为 , E为BC的中点,所以AE⊥BC. 又 BC∥AD,因此AE⊥AD.,因为PA⊥平面ABCD,AE平面ABCD,所以PA⊥AE.
而PA平面PAD,AD平面PAD 且PA∩AD=A,
所以 AE⊥平面PAD,又PD平面PAD.
所以 AE⊥PD
(Ⅱ)由(Ⅰ)由知AE,AD,AP两两垂直,以A为坐标原点,建立如图所示的空间直角坐标系,又E、F分别为BC、PC的中点,联,平面PAD,是直线HE与平面PAD所成的角,不妨设,则,在,
,当最小时,最大,,此时,由,得,,
,,,,
所以 设平面AEF的一法向量为则因此取因为 BD⊥AC,BD⊥PA,PA∩AC=A,所以 BD⊥平面AFC,
故为平面AFC的一法向量. , 又=(-),
所以 cos<m, >=
因为,二面角E-AF-C为锐角,所以所求二面角的余弦值为
6.(Ⅰ)证明:由等腰直角三角形有,CDDE,DE∥BC
又,面ACD,平面,平面,
平面平面。
(Ⅱ)由条件有PQ为的中位线,MN为梯形BCDE的中位线PQ∥DE,MN∥DE PQ∥MN M、N、P、Q四点共面.
(Ⅲ) 解:平面平面,交线为DE, ADDE
AD面BCDE AD、DC、DE两两互相垂直
可以以D为原点建立如图空间直角坐标系,
设AD=2(长度单位),则DC=2,BC=4,
则C(2,0,0),A(0,0,2),E(0,2,0),
B(2,4,0)
设异面直线BE与MQ所成的角为,∵MQ∥BC,
∴ ,
异面直线BE与MQ所成的角大小为.ACR为正三角形,=
异面直线BE与QM所成的角大小为
7.解:(Ⅰ)∵PD⊥面ABCD,AB面ABCD, ∴AB⊥PD,又AB⊥AD, ∴AB⊥面PAD.
又MN是△PAB的中位线, ∴MN∥AB,从而MN⊥面PAD.w.w.w.k.s.5.u.c.o.m ∴∠PMD为二面角P—MN—D的平面角,由已知,在Rt△PAD中,易证:∠PAD=60°,而M是PA的中点,∴∠PMD=120
即所求二面角P—MN—D的大小为120°.
(Ⅱ)令,不妨设AD=2,则,.
以D为原点,DA、DC、DP所在直线分别为x、y、z轴建立空间直角坐标系,则
D(0,0,0),N(1,2,),C(0,4x,0),
∴(1,2,),(1,2-4x,);
若∠CND为直角,则必有,即
于是有,解得.
∴当时,∠CND为直角.
8.解:(Ⅰ)以A为坐标原点AB,AD,AE所在的直线分别为x,y,z轴建立空间直角坐标系 则,,
做BD的中点F并连接CF,AF;由题意可得CF⊥BD且 又 ,所以C的坐标为 ,
(Ⅱ)设平面BCE的法向量为 则 即令x=1得 又
设平面DE与平面BCE所成角为,则 .
(III)假设存在点M使得CM∥面ADE,则
, 得
又因为, 所以
因为CM∥面ADE,则 即
得 故 点M为BE的中点时CM∥面ADE.
9.解:(Ⅰ)易知AB=2a,所以,因为四边形是矩形,所以,所以平面,所以平面A;所以平面;
(Ⅱ)设AC和BD交于K,所以AK:CK=2,所以AK=,
所以MF= AK=,即EM=
(III)经计算可知EF=,FB=,EB=,所以FEBF,
所以取EF中点为H,BE中点为N,DH=,HN=,DN=,
所以=
10.解:(Ⅰ)∵平面平面,
AE⊥EF,∴AE⊥平面,AE⊥EF,AE⊥BE,
又BE⊥EF,故可如图建立空间坐标系E-xyz.
,又为BC的中点,BC=4,
.则(-2,2,2),(2,2,0),(-2,2,2),(2,2,0)=0,∴.
(Ⅱ)∵AD∥面BFC,所以 =VA-BFC=
,即时有最大值为.
(Ⅲ)设平面DBF的法向量为,∵AE=2, B(2,0,0),D(0,2,2),F(0,3,0),∴(-2,2,2),
则 ,即,
取,∴
,面BCF一个法向量为,则cos<>=,由于所求二面角D-BF-C的平面角为钝角,所以此二面角的余弦值为-.
A
D
E
C
B
Q
A
D
E
C
B
M
N
P
A
D
E
C
B
P
A
B
C
D
M
N
A
D
B
C
V
x
y
z
P
A
B
C
D
M
N
x
y
z
F
z
x
y
H
D
F
E
C
B
M
A
N
x
y
z
祝你成功
1.如图,在棱长为1的正方体中,是侧棱上的一点,.
(Ⅰ)试确定,使得直线与平面所成角的正切值为;
(Ⅱ)在线段上是否存在一个定点,使得对任意的,在平面上的射影垂直于,并证明你的结论.
2.如图,在三棱锥V-ABC中,VC⊥底面ABC,AC⊥BC,D是AB的中点,且AC=BC=a,∠VDC=θ。(Ⅰ)求证:平面VAB⊥平面VCD ;
(Ⅱ)当角θ变化时,求直线BC与平面VAB所成的角的取值范围;
3.如图,棱柱中,都与平面所成的角相等,
∠CAB=90°,AC=AB=A1B=a,D为BC上的点,且A1C//平面ADB1。求:
(Ⅰ)A1C与平面ADB1的距离;(Ⅱ)二面角A1—AB—C的大小;
(Ⅲ)AB1与平面ABC所成的角的大小。
4.在四棱锥中,底面是菱形,.
(Ⅰ)若,求证:平面;
(Ⅱ)若平面平面,求证:;
(Ⅲ)在棱上是否存在点(异于点)使得∥平面,若存在,求的值;若不存在,说明理由.
5如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,,E,F分别是BC, PC的中点.
(Ⅰ)证明:AE⊥PD;
(Ⅱ)若H为PD上的动点,EH与平面PAD所成最大角的正切值为,求二面角E—AF—C的余弦值.
6.如图,沿等腰直角三角形的中位线,将平面折起(转动一定角度),得到四棱锥,设、、、的中点分别为、、、,平面⊥平面。
(Ⅰ)求证:平面⊥平面;(Ⅱ)求证:、、、四点共面;
(Ⅲ)求异面直线与所有的角。
7.在四棱锥中,,∥,⊥底面,,直线与底面成60°角,点分别是、的中点.
(Ⅰ)求二面角的大小;
(Ⅱ)当的值为多少时,为直角?
8.将边长为2的正方形ABCD沿对角线BD折叠,使得平面ABD⊥平面CBD,AE⊥平面ABD,且AE=.
(Ⅰ)求证:DE⊥AC;
(Ⅱ)求DE与平面BEC所成角的正弦值;
(Ⅲ)直线BE上是否存在一点M,使得CM∥平面ADE,
若存在,求点M的位置,不存在请说明理由.
9.如图,在梯形中,∥,,,平面平面,四边形是矩形,,点在线段上.
(Ⅰ)求证:平面;(Ⅱ)当为何值时,∥平面 证明你的结论;(Ⅲ)求二面角的平面角的余弦值。
10.已知梯形ABCD中,AD∥BC,∠ABC =∠BAD =,AB=BC=2AD=4,E、F分别是AB、CD上的点,EF∥BC,AE = x,G是BC的中点.沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF (如图).
(Ⅰ)当x=2时,求证:BD⊥EG ;
(Ⅱ)若以F、B、C、D为顶点的三棱锥的体积记为,求的最大值;
(Ⅲ)当取得最大值时,求二面角D-BF-C的余弦值.
2012考前金题巧练(1)参答
1.解:(Ⅰ)建立如图所示的空间直角坐标系,则A(1,0,0),B(1,1,0),P(0,1,m),C(0,1,0),D(0,0,0),B1(1,1,1),D1(0,0,1)所以又由知,为平面的一个法向量。设AP与平面所成的角为,则。依题意有解得。故当时,
直线AP与平面所成的角的正切值为。
(Ⅱ)若在A1C1上存在这样的点Q,设此点的横坐标为,则Q(x,1-,1),。依题意,对任意的m要使D1Q在平面APD1上的射影垂直于AP,等价于D1Q⊥AP即Q为A1C1的中点时,满足题设要求。
2.解:(Ⅰ)以所在的直线分别为轴、轴、轴,建立如图所示的空间直角坐标系,则,
于是,,,.
从而,即.
同理,
即.又,平面.
又平面.平面平面.
(Ⅱ)设直线与平面所成的角为,平面的一个法向量为,
则由.得
可取,又,
于是,
,,.又,.
即直线与平面所成角的取值范围为.
3.解:建立如图坐标系,则A(0,0,0)B(a,0,0),C(0,a,0)
连A1B,由条件知,△A1AB和△A1AC均为等边△且边长为a,
∴∠A1AB=∠A1AC=60°,设A(x,y,z),则
由
同理得
(I)A1C//面ADB1,∵A1C//ED,又E为A1B中点,∴D为BC中点,
∴D,设面ADB1的法向量
则取
设A1C面ADB1的距离为d,则
(Ⅱ)平面ABC的一个法向量为,设平面A1AB的法向量为
则,取
设,则
即二面角A1—AB—C的大小为
(Ⅲ)设AB1与平面ABC所成角为θ2,则
,即AB1与平面ABC所成角为
4.(Ⅰ)证明:因为 底面是菱形
所以 . 因为 ,,
所以 平面.
(Ⅱ)证明:由(Ⅰ)可知.
因为 平面平面,平面平面,平面,所以 平面. 因为 平面,
所以 . 因为 底面是菱形,所以 .所以 .
(Ⅲ)解:不存在. 下面用反证法说明. 假设存在点(异于点)使得∥平面.
在菱形中,∥,因为 平面,平面,所以 ∥平面. 因为 平面,平面,,所以 平面∥平面.而平面与平面相交,矛盾.
5(Ⅰ)证明:由四边形ABCD为菱形,∠ABC=60°,可得△ABC为正三角形.
因为 , E为BC的中点,所以AE⊥BC. 又 BC∥AD,因此AE⊥AD.,因为PA⊥平面ABCD,AE平面ABCD,所以PA⊥AE.
而PA平面PAD,AD平面PAD 且PA∩AD=A,
所以 AE⊥平面PAD,又PD平面PAD.
所以 AE⊥PD
(Ⅱ)由(Ⅰ)由知AE,AD,AP两两垂直,以A为坐标原点,建立如图所示的空间直角坐标系,又E、F分别为BC、PC的中点,联,平面PAD,是直线HE与平面PAD所成的角,不妨设,则,在,
,当最小时,最大,,此时,由,得,,
,,,,
所以 设平面AEF的一法向量为则因此取因为 BD⊥AC,BD⊥PA,PA∩AC=A,所以 BD⊥平面AFC,
故为平面AFC的一法向量. , 又=(-),
所以 cos<m, >=
因为,二面角E-AF-C为锐角,所以所求二面角的余弦值为
6.(Ⅰ)证明:由等腰直角三角形有,CDDE,DE∥BC
又,面ACD,平面,平面,
平面平面。
(Ⅱ)由条件有PQ为的中位线,MN为梯形BCDE的中位线PQ∥DE,MN∥DE PQ∥MN M、N、P、Q四点共面.
(Ⅲ) 解:平面平面,交线为DE, ADDE
AD面BCDE AD、DC、DE两两互相垂直
可以以D为原点建立如图空间直角坐标系,
设AD=2(长度单位),则DC=2,BC=4,
则C(2,0,0),A(0,0,2),E(0,2,0),
B(2,4,0)
设异面直线BE与MQ所成的角为,∵MQ∥BC,
∴ ,
异面直线BE与MQ所成的角大小为.ACR为正三角形,=
异面直线BE与QM所成的角大小为
7.解:(Ⅰ)∵PD⊥面ABCD,AB面ABCD, ∴AB⊥PD,又AB⊥AD, ∴AB⊥面PAD.
又MN是△PAB的中位线, ∴MN∥AB,从而MN⊥面PAD.w.w.w.k.s.5.u.c.o.m ∴∠PMD为二面角P—MN—D的平面角,由已知,在Rt△PAD中,易证:∠PAD=60°,而M是PA的中点,∴∠PMD=120
即所求二面角P—MN—D的大小为120°.
(Ⅱ)令,不妨设AD=2,则,.
以D为原点,DA、DC、DP所在直线分别为x、y、z轴建立空间直角坐标系,则
D(0,0,0),N(1,2,),C(0,4x,0),
∴(1,2,),(1,2-4x,);
若∠CND为直角,则必有,即
于是有,解得.
∴当时,∠CND为直角.
8.解:(Ⅰ)以A为坐标原点AB,AD,AE所在的直线分别为x,y,z轴建立空间直角坐标系 则,,
做BD的中点F并连接CF,AF;由题意可得CF⊥BD且 又 ,所以C的坐标为 ,
(Ⅱ)设平面BCE的法向量为 则 即令x=1得 又
设平面DE与平面BCE所成角为,则 .
(III)假设存在点M使得CM∥面ADE,则
, 得
又因为, 所以
因为CM∥面ADE,则 即
得 故 点M为BE的中点时CM∥面ADE.
9.解:(Ⅰ)易知AB=2a,所以,因为四边形是矩形,所以,所以平面,所以平面A;所以平面;
(Ⅱ)设AC和BD交于K,所以AK:CK=2,所以AK=,
所以MF= AK=,即EM=
(III)经计算可知EF=,FB=,EB=,所以FEBF,
所以取EF中点为H,BE中点为N,DH=,HN=,DN=,
所以=
10.解:(Ⅰ)∵平面平面,
AE⊥EF,∴AE⊥平面,AE⊥EF,AE⊥BE,
又BE⊥EF,故可如图建立空间坐标系E-xyz.
,又为BC的中点,BC=4,
.则(-2,2,2),(2,2,0),(-2,2,2),(2,2,0)=0,∴.
(Ⅱ)∵AD∥面BFC,所以 =VA-BFC=
,即时有最大值为.
(Ⅲ)设平面DBF的法向量为,∵AE=2, B(2,0,0),D(0,2,2),F(0,3,0),∴(-2,2,2),
则 ,即,
取,∴
,面BCF一个法向量为,则cos<>=,由于所求二面角D-BF-C的平面角为钝角,所以此二面角的余弦值为-.
A
D
E
C
B
Q
A
D
E
C
B
M
N
P
A
D
E
C
B
P
A
B
C
D
M
N
A
D
B
C
V
x
y
z
P
A
B
C
D
M
N
x
y
z
F
z
x
y
H
D
F
E
C
B
M
A
N
x
y
z
同课章节目录
