2020--2021学年人教版八年级数学 下册 第二十章 数据的分析 单元综合与测试 A卷(word含答案)
文档属性
| 名称 | 2020--2021学年人教版八年级数学 下册 第二十章 数据的分析 单元综合与测试 A卷(word含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 104.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-31 00:00:00 | ||
图片预览


文档简介
第二十章
数据的分析
单元复习与检测题
A卷(含答案)
一、选择题
1、在今年的助残募捐活动中,我市某中学九年级(1)班同学组织献爱心捐款活动,班长根据第一组12名同学捐款情况绘制成如图的条形统计图.根据图中提供的信息,第一组捐款金额的平均数是
( )
A.20元
B.15元
C.12元
D.10元
2、为了解乡镇企业的水资源的利用情况,市水利管理部门抽查了部分乡镇企业在一个月中的用水情况,其中用水15吨的有3家,用水20吨的有5家,用水30吨的有7家,那么平均每家企业1个月用水(
).
A.23.7吨
B.21.6吨
C.20吨
D.5.416吨
3、m个x1,n个x2和r个x3,由这些数据组成一组数据的平均数是(
).
A.
B.
C.
D.
4、随着时代的发展,许多人开始注重精神的享受,应运而生的便是旅游的兴起.有人对南山旅游人数做了10天统计,结果有3天是每天800人,有2天是每天1200人,有5天是每天700人,那么这10天平均每天的旅游人数是(
)
A.830人
B.850人
C.900人
D.800人
5、某辆汽车从甲地以速度v1匀速行驶至乙地后,又从乙地以速度v2匀速返回甲地,则汽车在这个行驶过程中的平均速度是(
).
A.
B.
C.
D.
6、已知一组数据从小到大排列为-1,0,4,x,6,15,且这组数据的中位数为5,那么这组数据的众数为(
)
A.5
B.6
C.4
D.5.5
7、某班一次英语测验的成绩如下,得98分的7人,90分的4人,80分的17人,70分的8人,60分的3人,50分的1人,这里80分是( )
A.是平均数
B.
只是众数
C.
只是中位数
D.既是众数又是中位数
8、一组数据-1,0,3,5,x的极差是7,那么x的值可能有(
).
A.1个
B.2个
C.4个
D.6个
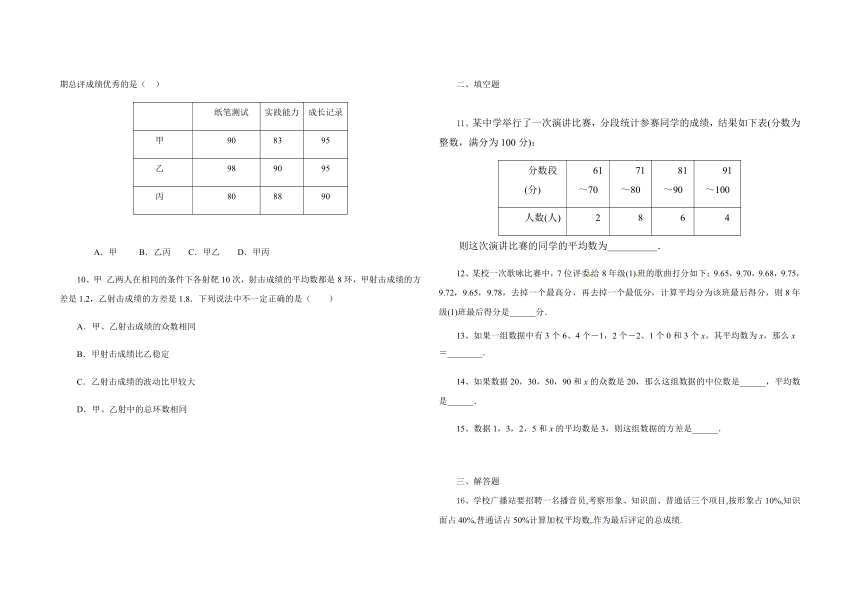
9、某校把学生的纸笔测试、实践能力、成长纪录三项成绩分别按50%、20%、30%的比例计入学期总评成绩,90分以上为优秀.甲、乙、丙三人的各项成绩如下表(单位:分),学期总评成绩优秀的是(
)
纸笔测试
实践能力
成长记录
甲
90
83
95
乙
98
90
95
丙
80
88
90
A.甲
B.乙丙
C.甲乙
D.甲丙
10、甲
乙两人在相同的条件下各射靶10次,射击成绩的平均数都是8环,甲射击成绩的方差是1.2,乙射击成绩的方差是1.8.下列说法中不一定正确的是( )
A.甲、乙射击成绩的众数相同
B.甲射击成绩比乙稳定
C.乙射击成绩的波动比甲较大
D.甲、乙射中的总环数相同
填空题
11、某中学举行了一次演讲比赛,分段统计参赛同学的成绩,结果如下表(分数为整数,满分为100分):
分数段(分)
61~70
71~80
81~90
91~100
人数(人)
2
8
6
4
则这次演讲比赛的同学的平均数为__________.
12、某校一次歌咏比赛中,7位评委给8年级(1)班的歌曲打分如下:9.65,9.70,9.68,9.75,9.72,9.65,9.78,去掉一个最高分,再去掉一个最低分,计算平均分为该班最后得分,则8年级(1)班最后得分是______分.
13、如果一组数据中有3个6、4个-1,2个-2、1个0和3个x,其平均数为x,那么x=________.
14、如果数据20,30,50,90和x的众数是20,那么这组数据的中位数是______,平均数是______.
15、数据1,3,2,5和x的平均数是3,则这组数据的方差是______.
三、解答题
16、学校广播站要招聘一名播音员,考察形象、知识面、普通话三个项目,按形象占10%,知识面占40%,普通话占50%计算加权平均数,作为最后评定的总成绩.
李文和孔明两位同学的各项成绩如下表:
项目
选手
形象
知识面
普通话
李文
70
80
88
孔明
80
75
x
(1)计算李文同学的总成绩;
(2)若孔明同学要在总成绩上超过李文同学,则他的普通话成绩x应超过多少分?
17、甲、乙两支仪仗队队员的身高(单位:厘米)如下:
甲队:178
177
179
178
177
178
177
179
178
179;
乙队:178
179
176
178
180
178
176
178
177
180.
(1)将下表填完整:
身高(厘米)
176
177
178
179
180
甲队(人数)
3
4
0
乙队(人数)
2
1
1
(2)甲队队员身高的平均数为______厘米,乙队队员身高的平均数为______厘米;
(3)你认为哪支仪仗队更为整齐?简要说明理由.
18、古往今来,地球妈妈用乳汁哺育了无数代子孙,现在,人类为了自身利益,将她折磨的天昏地暗,地球正面临严峻的环境危机.为了保护环境,某校环保小组成员小明收集废电池,第一天收集1号电池4节,5号电池5节,总质量为450g;第二天收集1号电池2节,5号电池3节,总质量为240g.
(1)求1号电池和5号电池每节分别重多少克;
(2)学校环保小组为估算四月份收集废电池的总质量,随意抽取了该月某5天每天收集废电池的数量如下表:
1号废电池(单位:节)
29
30
32
28
31
5号废电池(单位:节)
51
53
47
49
50
分别计算两种废电池的样本数据的平均数,并由此估算该月(30天)环保小组收集废电池的总质量是多少千克;
(3)试说明上述表格中数据的获取方法.你认为这种方法合理吗?
19、在学校组织的某知识竞赛中,每班参加比赛的人数相同,成绩分为A,B,C,D四个等级,其中相应等级的得分依次记为100分,90分,80分,70分,学校将某年级一班和二班的成绩整理并绘制成统计图(如图):
请你根据以上提供的信息解答下列问题:
(1)此次竞赛中二班成绩在C级以上(包括C级)的人数为
.
(2)请你将表格补充完整:
平均数(分)
中位数(分)
众数(分)
一班
87.6
90
二班
87.6
100
(3)请从下列不同角度对这次竞赛的成绩进行分析:
①从平均数和中位数的角度来比较一班和二班的成绩;
②从平均数和众数的角度来比较一班和二班的成绩;
③从B级以上(包括B级)的人数的角度来比较一班和二班的成绩
20、课外活动,甲、乙、丙、丁四位同学进行乒乓球单循环赛,比赛分六场进行,每场采用“7局4胜制”.右表是他们比赛后的成绩统计表,表中①与②表示同一场比赛的比分(①是指甲以0:4负于丁,②是指丁以4:0胜于甲),其余场次记法相同。
(1)问这次比赛谁是冠军,说明理由;
(2)求这六场比赛每场进行的总局数的中位数和众数.
甲
乙
丙
丁
甲
4:0
2:4
0:4①
乙
0:4
2:4
3:4
丙
4:2
4:2
4:0
丁
4:0②
4:3
0:4
21.为迎接“外研社杯”全国英语演讲大赛.某市举行优秀学生选拔赛,学校为了迎接比赛,特组织学生进行英语口语比赛训练,把20名学生分成甲、乙两个小组,训练测试成绩如下(单位:分)
甲组:76,90,84,86,87,86,81,82,83,85;
乙组:82,84,85,89,79,91,89,80,79,74.
根据学过的知识判断哪个小组学生的成绩比较整齐.
22、在某旅游景区上山的一条小路上,有一些断断续续的台阶,下图是其中的甲、乙两段台阶的示意图.请你用所学过的有关统计的知识(平均数、中位数、方差和极差)回答下列问题:
(1)两段台阶路有哪些相同点和不同点?
(2)哪段台阶路走起来更舒服?为什么?
(3)为方便游客行走,需要重新整修上山的小路.对于这两段台阶路,在台阶数不变的情况下,请你提出合理的整修建议.(图中的数字表示每一级台阶的高度(单位:cm).并且数据15,16,16,14,14,15的方差S甲2=,数据11,15,18,17,10,19的方差S乙2=).
参考答案:
一、1、D
2、A
3、D
4、A
5、D
6、B
7、D
8、B
9、C
10、A
二、
11、81.5分
12、9.70
13、1
14、30,42
15、2
三、16、解:
(1)李文同学的总成绩为
70×10%+80×40%+88×50%=83(分)
(2)
孔明同学的总成绩为80×10%+75×40%+50%·x.
根据题意,得80×10%+75×40%+50%·x﹥83,
解得x﹥90.
答:若孔明同学要在总成绩上超过李文同学,则他的普通话成绩超过90分.
17、(1)略;(2)178,178;(3)甲队,理由略.
18、解:(1)设每节1号电池重xg,每节5号电池重yg.
依题意可列方程组为
解得即1号电池每节重75g,5号电池每节重30g.
(2)1号废电池的样本数据的平均数为=30(节),
5号废电池的样本数据的平均数为=50(节)
所以估计每天可收集的废电池总质量为30×75+50×30=3750(g),
所以估计该月(30天)环保小组收集废电池的总质量是3750×30=112500(g),即112.5kg
(3)上述表格中数据的获取方法是抽样调查,且由抽样的“随意性”知,这种抽样调查方法是合理的。
19、解:(1)21
(2)一班众数为90,二班中位数为80
(3)①从平均数的角度看,两班成绩一样;从中位数的角度看,一班比二班的成绩好.
②从平均数的角度看,两班成绩一样;从众数的角度看,二班比一班的成绩好.
③从B级以上(包括B级)的人数的角度看,一班人数是18,二班人数是12,所以一班成绩好。
20、【答案】(1)甲胜1场,乙胜0场,丙胜3场,丁胜2场,所以丙是冠军;
(2)每场进行的总局数是4、6、6、4、7、4;
对局数进行从小到大的排列即4、4、4、6、6、7
由此可知:中位数是5。
众数是4。
21、解:=(76+90+84+86+87+86+81+82+83+85)=84(分),
=(82+84+85+89+79+91+89+80+79+74)=83.2(分),
∴=×[(76-84)2+(90-84)2+…+(85-4)2]=13.2,
=×[(82-83.2)2+(84-83.2)2+…+(74-83.2)2]=26.36.
∵<,
∴甲组学生的成绩比较整齐.
22、(1)相同点:两段台阶路台阶高度的平均数相同.
不同点:两段台阶路台阶高度的中位数、方差和极差均不相同.
(2)甲段路走起来更舒服一些,因为它的台阶高度的方差小.
(3)每个台阶高度均为15cm(原平均数)使得方差为0.
数据的分析
单元复习与检测题
A卷(含答案)
一、选择题
1、在今年的助残募捐活动中,我市某中学九年级(1)班同学组织献爱心捐款活动,班长根据第一组12名同学捐款情况绘制成如图的条形统计图.根据图中提供的信息,第一组捐款金额的平均数是
( )
A.20元
B.15元
C.12元
D.10元
2、为了解乡镇企业的水资源的利用情况,市水利管理部门抽查了部分乡镇企业在一个月中的用水情况,其中用水15吨的有3家,用水20吨的有5家,用水30吨的有7家,那么平均每家企业1个月用水(
).
A.23.7吨
B.21.6吨
C.20吨
D.5.416吨
3、m个x1,n个x2和r个x3,由这些数据组成一组数据的平均数是(
).
A.
B.
C.
D.
4、随着时代的发展,许多人开始注重精神的享受,应运而生的便是旅游的兴起.有人对南山旅游人数做了10天统计,结果有3天是每天800人,有2天是每天1200人,有5天是每天700人,那么这10天平均每天的旅游人数是(
)
A.830人
B.850人
C.900人
D.800人
5、某辆汽车从甲地以速度v1匀速行驶至乙地后,又从乙地以速度v2匀速返回甲地,则汽车在这个行驶过程中的平均速度是(
).
A.
B.
C.
D.
6、已知一组数据从小到大排列为-1,0,4,x,6,15,且这组数据的中位数为5,那么这组数据的众数为(
)
A.5
B.6
C.4
D.5.5
7、某班一次英语测验的成绩如下,得98分的7人,90分的4人,80分的17人,70分的8人,60分的3人,50分的1人,这里80分是( )
A.是平均数
B.
只是众数
C.
只是中位数
D.既是众数又是中位数
8、一组数据-1,0,3,5,x的极差是7,那么x的值可能有(
).
A.1个
B.2个
C.4个
D.6个
9、某校把学生的纸笔测试、实践能力、成长纪录三项成绩分别按50%、20%、30%的比例计入学期总评成绩,90分以上为优秀.甲、乙、丙三人的各项成绩如下表(单位:分),学期总评成绩优秀的是(
)
纸笔测试
实践能力
成长记录
甲
90
83
95
乙
98
90
95
丙
80
88
90
A.甲
B.乙丙
C.甲乙
D.甲丙
10、甲
乙两人在相同的条件下各射靶10次,射击成绩的平均数都是8环,甲射击成绩的方差是1.2,乙射击成绩的方差是1.8.下列说法中不一定正确的是( )
A.甲、乙射击成绩的众数相同
B.甲射击成绩比乙稳定
C.乙射击成绩的波动比甲较大
D.甲、乙射中的总环数相同
填空题
11、某中学举行了一次演讲比赛,分段统计参赛同学的成绩,结果如下表(分数为整数,满分为100分):
分数段(分)
61~70
71~80
81~90
91~100
人数(人)
2
8
6
4
则这次演讲比赛的同学的平均数为__________.
12、某校一次歌咏比赛中,7位评委给8年级(1)班的歌曲打分如下:9.65,9.70,9.68,9.75,9.72,9.65,9.78,去掉一个最高分,再去掉一个最低分,计算平均分为该班最后得分,则8年级(1)班最后得分是______分.
13、如果一组数据中有3个6、4个-1,2个-2、1个0和3个x,其平均数为x,那么x=________.
14、如果数据20,30,50,90和x的众数是20,那么这组数据的中位数是______,平均数是______.
15、数据1,3,2,5和x的平均数是3,则这组数据的方差是______.
三、解答题
16、学校广播站要招聘一名播音员,考察形象、知识面、普通话三个项目,按形象占10%,知识面占40%,普通话占50%计算加权平均数,作为最后评定的总成绩.
李文和孔明两位同学的各项成绩如下表:
项目
选手
形象
知识面
普通话
李文
70
80
88
孔明
80
75
x
(1)计算李文同学的总成绩;
(2)若孔明同学要在总成绩上超过李文同学,则他的普通话成绩x应超过多少分?
17、甲、乙两支仪仗队队员的身高(单位:厘米)如下:
甲队:178
177
179
178
177
178
177
179
178
179;
乙队:178
179
176
178
180
178
176
178
177
180.
(1)将下表填完整:
身高(厘米)
176
177
178
179
180
甲队(人数)
3
4
0
乙队(人数)
2
1
1
(2)甲队队员身高的平均数为______厘米,乙队队员身高的平均数为______厘米;
(3)你认为哪支仪仗队更为整齐?简要说明理由.
18、古往今来,地球妈妈用乳汁哺育了无数代子孙,现在,人类为了自身利益,将她折磨的天昏地暗,地球正面临严峻的环境危机.为了保护环境,某校环保小组成员小明收集废电池,第一天收集1号电池4节,5号电池5节,总质量为450g;第二天收集1号电池2节,5号电池3节,总质量为240g.
(1)求1号电池和5号电池每节分别重多少克;
(2)学校环保小组为估算四月份收集废电池的总质量,随意抽取了该月某5天每天收集废电池的数量如下表:
1号废电池(单位:节)
29
30
32
28
31
5号废电池(单位:节)
51
53
47
49
50
分别计算两种废电池的样本数据的平均数,并由此估算该月(30天)环保小组收集废电池的总质量是多少千克;
(3)试说明上述表格中数据的获取方法.你认为这种方法合理吗?
19、在学校组织的某知识竞赛中,每班参加比赛的人数相同,成绩分为A,B,C,D四个等级,其中相应等级的得分依次记为100分,90分,80分,70分,学校将某年级一班和二班的成绩整理并绘制成统计图(如图):
请你根据以上提供的信息解答下列问题:
(1)此次竞赛中二班成绩在C级以上(包括C级)的人数为
.
(2)请你将表格补充完整:
平均数(分)
中位数(分)
众数(分)
一班
87.6
90
二班
87.6
100
(3)请从下列不同角度对这次竞赛的成绩进行分析:
①从平均数和中位数的角度来比较一班和二班的成绩;
②从平均数和众数的角度来比较一班和二班的成绩;
③从B级以上(包括B级)的人数的角度来比较一班和二班的成绩
20、课外活动,甲、乙、丙、丁四位同学进行乒乓球单循环赛,比赛分六场进行,每场采用“7局4胜制”.右表是他们比赛后的成绩统计表,表中①与②表示同一场比赛的比分(①是指甲以0:4负于丁,②是指丁以4:0胜于甲),其余场次记法相同。
(1)问这次比赛谁是冠军,说明理由;
(2)求这六场比赛每场进行的总局数的中位数和众数.
甲
乙
丙
丁
甲
4:0
2:4
0:4①
乙
0:4
2:4
3:4
丙
4:2
4:2
4:0
丁
4:0②
4:3
0:4
21.为迎接“外研社杯”全国英语演讲大赛.某市举行优秀学生选拔赛,学校为了迎接比赛,特组织学生进行英语口语比赛训练,把20名学生分成甲、乙两个小组,训练测试成绩如下(单位:分)
甲组:76,90,84,86,87,86,81,82,83,85;
乙组:82,84,85,89,79,91,89,80,79,74.
根据学过的知识判断哪个小组学生的成绩比较整齐.
22、在某旅游景区上山的一条小路上,有一些断断续续的台阶,下图是其中的甲、乙两段台阶的示意图.请你用所学过的有关统计的知识(平均数、中位数、方差和极差)回答下列问题:
(1)两段台阶路有哪些相同点和不同点?
(2)哪段台阶路走起来更舒服?为什么?
(3)为方便游客行走,需要重新整修上山的小路.对于这两段台阶路,在台阶数不变的情况下,请你提出合理的整修建议.(图中的数字表示每一级台阶的高度(单位:cm).并且数据15,16,16,14,14,15的方差S甲2=,数据11,15,18,17,10,19的方差S乙2=).
参考答案:
一、1、D
2、A
3、D
4、A
5、D
6、B
7、D
8、B
9、C
10、A
二、
11、81.5分
12、9.70
13、1
14、30,42
15、2
三、16、解:
(1)李文同学的总成绩为
70×10%+80×40%+88×50%=83(分)
(2)
孔明同学的总成绩为80×10%+75×40%+50%·x.
根据题意,得80×10%+75×40%+50%·x﹥83,
解得x﹥90.
答:若孔明同学要在总成绩上超过李文同学,则他的普通话成绩超过90分.
17、(1)略;(2)178,178;(3)甲队,理由略.
18、解:(1)设每节1号电池重xg,每节5号电池重yg.
依题意可列方程组为
解得即1号电池每节重75g,5号电池每节重30g.
(2)1号废电池的样本数据的平均数为=30(节),
5号废电池的样本数据的平均数为=50(节)
所以估计每天可收集的废电池总质量为30×75+50×30=3750(g),
所以估计该月(30天)环保小组收集废电池的总质量是3750×30=112500(g),即112.5kg
(3)上述表格中数据的获取方法是抽样调查,且由抽样的“随意性”知,这种抽样调查方法是合理的。
19、解:(1)21
(2)一班众数为90,二班中位数为80
(3)①从平均数的角度看,两班成绩一样;从中位数的角度看,一班比二班的成绩好.
②从平均数的角度看,两班成绩一样;从众数的角度看,二班比一班的成绩好.
③从B级以上(包括B级)的人数的角度看,一班人数是18,二班人数是12,所以一班成绩好。
20、【答案】(1)甲胜1场,乙胜0场,丙胜3场,丁胜2场,所以丙是冠军;
(2)每场进行的总局数是4、6、6、4、7、4;
对局数进行从小到大的排列即4、4、4、6、6、7
由此可知:中位数是5。
众数是4。
21、解:=(76+90+84+86+87+86+81+82+83+85)=84(分),
=(82+84+85+89+79+91+89+80+79+74)=83.2(分),
∴=×[(76-84)2+(90-84)2+…+(85-4)2]=13.2,
=×[(82-83.2)2+(84-83.2)2+…+(74-83.2)2]=26.36.
∵<,
∴甲组学生的成绩比较整齐.
22、(1)相同点:两段台阶路台阶高度的平均数相同.
不同点:两段台阶路台阶高度的中位数、方差和极差均不相同.
(2)甲段路走起来更舒服一些,因为它的台阶高度的方差小.
(3)每个台阶高度均为15cm(原平均数)使得方差为0.
