2020--2021学年人教版八年级数学 下册 第二十章 数据的分析 单元综合与测试 B卷(word含答案)
文档属性
| 名称 | 2020--2021学年人教版八年级数学 下册 第二十章 数据的分析 单元综合与测试 B卷(word含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 198.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-31 22:11:10 | ||
图片预览


文档简介
第二十章
数据的分析
单元复习与检测题
B卷(含答案)
一、选择题
1、某校开展“节约每一滴水”活动,为了了解开展活动一个月以来节约用水的情况,从八年级的400名同学中选取20名同学统计了各自家庭一个月的节水情况,如下表:
节水量/m3
0.2
0.25
0.3
0.4
0.5
家庭数/个
2
4
6
7
1
请你估计这400名同学的家庭一个月节约用水的总量大约是
( )
A.130
m3
B.135
m3
C.6.5
m3
D.260
m3
2、某同学使用计算器求30个数据的平均数时,错将其中一个数据105输入为15,那么由此求出的平均数与实际平均数的差为
( )
A.35
B.3
C.0.5
D.-3
3、某居民大院月底统计用电情况,其中3户用电45度,5户用电50度,6户用电42度,则每户平均用电(
).
A.41度
B.42度
C.45.5度
D.46度
4、在今年的助残募捐活动中,我市某中学九年级(1)班的同学组织献爱心捐款活动,班长根据第一组12名同学的捐款情况绘制成如图所示的条形统计图.根据图中提供的信息,第一组同学捐款金额的平均数是(
)
A.20元
B.15元
C.12元
D.10元
5、某同学在用计算器求30个数据的平均数时,错将其中一个数据105输入为15,那么由此算出的平均数与实际平均数的差为(
).
A.3
B.-3
C.3.5
D.-3.5
6、七年级学生完成课题学习“从数据谈节水”后,积极践行“节约用水,从我做起”.下表是从七年级400名学生中选出的10名学生统计的各自家庭一个月的节水情况:
节水量(m3)
0.2
0.25
0.3
0.4
0.5
家庭数(个)
1
2
2
4
1
那么这组数据的众数和平均数分别是(
)
A.0.4和0.34
B.0.4和0.3
C.0.25和0.34
D.0.25和0.3
7、下列说法正确的是( )
A.
样本7,7,6,5,4的众数是2
B.
若数据x1,x2,…xn的平均数是x,则(x1-x)+(x2-x)+…+(xn-x)=0
C.
样本1,2,3,4,5,6的中位数是4
D.
样本50,50,39,41,41不存在众数
8、已知样本数据1,2,4,3,5,下列说法不正确的是(
).
A.平均数是3
B.中位数是4
C.极差是4
D.方差是2
9、对于数据3,3,2,3,6,3,10,3,6,3,2.①这组数据的众数是3;②这组数据的众数与中位数的数值不等;③这组数据的中位数与平均数的数值相等;④这组数据的平均数与众数的数值相等,其中正确的结论有(
)
A.1个
B.2个
C.3个
D.4个
10、茶叶厂用甲.乙两台包装机分装质量为400克的茶叶,从它们各自分装的茶叶中分别随机抽取10盒,测得它们实际质量的平均数和标准差分别如表所示,则包装茶叶质量较稳定的包装机为( )
A.甲
B.乙
C.甲和乙
D.无法确定
填空题
11、如果10名学生的平均身高为1.65米,其中2名学生的平均身高为1.75米,那么余下8名学生的平均身高是______米.
12、某学校举行演讲比赛,5位评委对某选手打分如下:(单位:分)9.5,9.4,9.4,9.5,9.2,则这个选手的平均分为
分.
13、一个样本的方差[(x1-3)2+(x2-3)2+…+(xn-3)2],则样本容量是______,样本平均数是______.
14、小明家去年的旅游、教育、饮食支出分别出3600元,1200元,7200元,今年这三项支出依次比去年增长10%,20%,30%,则小时家今年的总支出比去年增长的百分数是_________.
15、甲乙两地9月上旬的日平均气温如图所示,则甲乙两地这10天日平均气温方差大小关系为
(填>或<).
三、解答题
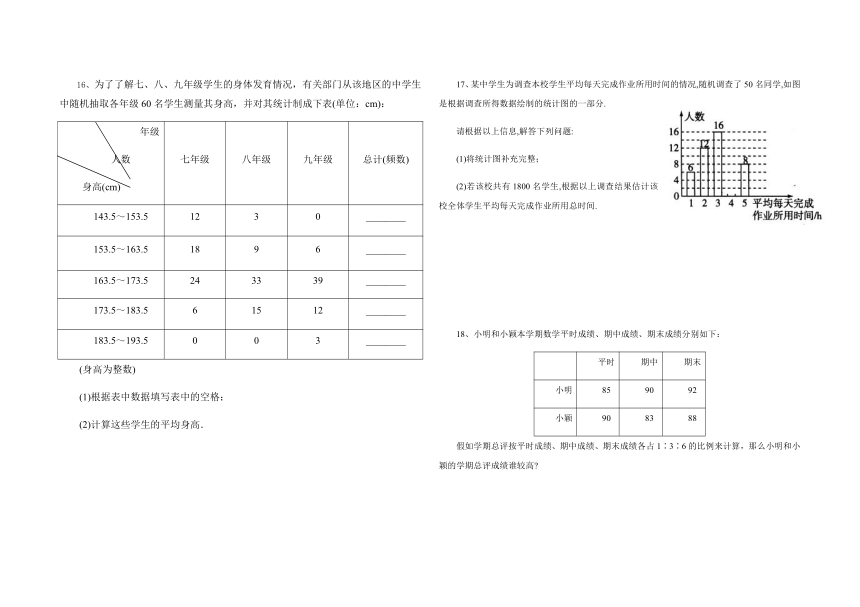
16、为了了解七、八、九年级学生的身体发育情况,有关部门从该地区的中学生中随机抽取各年级60名学生测量其身高,并对其统计制成下表(单位:cm):
年级
人数
身高(cm)
七年级
八年级
九年级
总计(频数)
143.5~153.5
12
3
0
________
153.5~163.5
18
9
6
________
163.5~173.5
24
33
39
________
173.5~183.5
6
15
12
________
183.5~193.5
0
0
3
________
(身高为整数)
(1)根据表中数据填写表中的空格;
(2)计算这些学生的平均身高.
17、某中学生为调查本校学生平均每天完成作业所用时间的情况,随机调查了50名同学,如图是根据调查所得数据绘制的统计图的一部分.
请根据以上信息,解答下列问题:
(1)将统计图补充完整;
(2)若该校共有1800名学生,根据以上调查结果估计该校全体学生平均每天完成作业所用总时间.
18、小明和小颖本学期数学平时成绩、期中成绩、期末成绩分别如下:
平时
期中
期末
小明
85
90
92
小颖
90
83
88
假如学期总评按平时成绩、期中成绩、期末成绩各占1∶3∶6的比例来计算,那么小明和小颖的学期总评成绩谁较高?
19、针对我国资源环境的具体情况,国家实行“限塑令”。“限塑令”执行前,某校为了了解本校学生所在家庭使用塑料袋的数量情况,随机调查了10名学生所在家庭每月使用塑料袋的数量,结果如下(单位:只)
65
70
85
75
79
74
91
81
95
85
(1)计算这10名学生所在家庭平均每月使用塑料袋多少只?
(2)“限塑令”执行后,家庭每月使用塑料袋数量预计将减少50%.根据上面的计算结果,估计该校1000名学生所在家庭每月使用塑料袋可减少多少只?
20、某高科技产品开发公司现有员工50名,所有员工的月工资情况如下表:
员工
管理人员
普通工作人员
人员结构
总经理
部门经理
科研人员
销售人员
高级技工
中级技工
勤杂工
员工数
1
3
2
3
24
1
每人月工资/元
21000
8400
2025
2200
1800
1600
950
请你根据上述内容,解答下列问题:
(1)该公司“高级技工”有
名;
(2)所有员工月工资的平均数为2500元,中位数为
元,众数为
元;
(3)小张到这家公司应聘普通工作人员,请你回答图中小王的问题,并指出用(2)中的哪个数据向小王介绍员工的月工资实际水平更合理些;
(4)去掉四个管理人员的工资后,请你计算出其他员工的月平均工资(结果保留整数),并判断能否反映该公司员工的月工资实际水平.
21、为了普及环保知识,增强环保意识,某中学组织了环保知识竞赛活动,初中三年级根据预选成绩选出了3名同学甲、乙、丙参加决赛,决赛要进行十次测试,三名选手的决赛成绩(满分为100分)如下表所示:
决赛成绩(单位:分)
甲
80
86
74
80
80
88
88
89
91
99
乙
85
85
87
97
85
76
88
77
87
88
丙
82
80
78
78
81
96
97
88
89
86
(1)请你填写下表:
平均数
众数
中位数
甲
85.5
87
乙
85.5
85
丙
84
(2)请从以下两个不同的角度对三个同学的决赛成绩进行分析:
①从平均数和众数相结合看,分析哪个同学成绩好些;
②从平均数和中位数相结合看,分析哪个同学成绩好些。
(3)如果在参加决赛的三名选手中选出1人参加市各中学总决赛,你认为哪个同学比较合适?并说明理由。
22、已知甲、乙两位同学11次测验成绩如图所示(单位:分):
(1)他们的平均成绩分别是多少?
(2)他们的测验成绩的方差是多少?
(3)现要从中选出一人参加比赛,历届比赛表明,成绩达到98分以上才能进入决赛,你认为应选谁参加这次比赛,为什么?
(4)分析两名同学的成绩各有何特点?并对两名同学各提一条学习建议
参考答案:
一、1、A
2、D
3、C
4、D
5、B
6、A
7、B
8、B
9、A
10、B
二、
11、1.625
12、9.4
13、12;3
14、27.3%
15、>
三、16、
年级
人数
身高(cm)
七年级
八年级
九年级
总计(频数)
143.5~153.5
12
3
0
__15__
153.5~163.5
18
9
6
__33__
163.5~173.5
24
33
39
__96__
173.5~183.5
6
15
12
__33__
183.5~193.5
0
0
3
__3__
解:(2)各组的组中值分别为148.5,158.5,168.5,178.5,188.5,=≈167(cm),即这些学生的平均身高约为167cm.
17、解:(1)50-6-12-16-8=8,补充完整的统计图如图所示.
(2)由上述统计图可得
==3(h).估计该校全体学生平均每天完成作业所用总时间为3×1800=5400(h).
18、小明
19、(1)80;
(2)4000.
20、思路建立(1)根据员工共有50人可求得高级技工的人数;
(2)根据中位数、众数的定义即可求出中位数、众数;
(3)平均数受极端值影响较大,不能代表全体员工工资的平均水平;
(4)计算后,再进行判断.
解:(1)16
(2)1700;1600
(3)这个老板的介绍不能反映该公司员工的月工资实际水平用中位数或众数来介绍更合理些.
(4)=≈1713(元),
能反映该公司员工的月工资实际水平.
21、【答案】(1)平均数:85.5;众数80,78;中位数86
(2)①∵平均数都相同,乙的众数最高,∴乙的成绩好一些;
②∵平均数都相同,甲的中位数最高,∴甲的成绩好一些.
(3)应选甲,理由是:
①中位数高说明有一半次数的分数在8以上,乙和丙达不到;
②从各次考试成绩可以看出,甲对环保知识很了解,成绩从第三次后一直在进步,说明甲平时重视环保知识,并且目前正在收集学习环保知识,他的知识面也越来越广.乙和丙后阶段成绩进步不够特出。
22、分析:对于(1)(2)根据定义及统计图中给出的数据计算即可;对于(3)应选成成绩达到98分以上的次数多的选手参加比赛;
(4)根据上面的计算结果提出建议即可.
解:(1)=×(99+100+100+95+93+90+98+100+93+90+98)=96,=×(98+99+96+94+95+92+92+98+96+99+97)=96.
即甲的平均成绩是96分,乙的平均成绩是96分.
(2)=[(99-96)2+(100-96)2+…+(98-96)2]≈14.18,
=[(98-96)2+(99-96)2+…+(97-96)2]≈5.82.
即甲的方差是14.18,乙的方差是5.82.
(3)选甲.因为11次测验中甲有4次测验成绩超过98分,而乙只有2次超过98分.
(4)由(2)(3)知乙的成绩稳定,甲的成绩波动较大,但是甲的高分率较高,有潜力.
建议:甲在今后的学习中应使成绩保持稳定,乙在今后的学习中应不断努力,提高高分率.
数据的分析
单元复习与检测题
B卷(含答案)
一、选择题
1、某校开展“节约每一滴水”活动,为了了解开展活动一个月以来节约用水的情况,从八年级的400名同学中选取20名同学统计了各自家庭一个月的节水情况,如下表:
节水量/m3
0.2
0.25
0.3
0.4
0.5
家庭数/个
2
4
6
7
1
请你估计这400名同学的家庭一个月节约用水的总量大约是
( )
A.130
m3
B.135
m3
C.6.5
m3
D.260
m3
2、某同学使用计算器求30个数据的平均数时,错将其中一个数据105输入为15,那么由此求出的平均数与实际平均数的差为
( )
A.35
B.3
C.0.5
D.-3
3、某居民大院月底统计用电情况,其中3户用电45度,5户用电50度,6户用电42度,则每户平均用电(
).
A.41度
B.42度
C.45.5度
D.46度
4、在今年的助残募捐活动中,我市某中学九年级(1)班的同学组织献爱心捐款活动,班长根据第一组12名同学的捐款情况绘制成如图所示的条形统计图.根据图中提供的信息,第一组同学捐款金额的平均数是(
)
A.20元
B.15元
C.12元
D.10元
5、某同学在用计算器求30个数据的平均数时,错将其中一个数据105输入为15,那么由此算出的平均数与实际平均数的差为(
).
A.3
B.-3
C.3.5
D.-3.5
6、七年级学生完成课题学习“从数据谈节水”后,积极践行“节约用水,从我做起”.下表是从七年级400名学生中选出的10名学生统计的各自家庭一个月的节水情况:
节水量(m3)
0.2
0.25
0.3
0.4
0.5
家庭数(个)
1
2
2
4
1
那么这组数据的众数和平均数分别是(
)
A.0.4和0.34
B.0.4和0.3
C.0.25和0.34
D.0.25和0.3
7、下列说法正确的是( )
A.
样本7,7,6,5,4的众数是2
B.
若数据x1,x2,…xn的平均数是x,则(x1-x)+(x2-x)+…+(xn-x)=0
C.
样本1,2,3,4,5,6的中位数是4
D.
样本50,50,39,41,41不存在众数
8、已知样本数据1,2,4,3,5,下列说法不正确的是(
).
A.平均数是3
B.中位数是4
C.极差是4
D.方差是2
9、对于数据3,3,2,3,6,3,10,3,6,3,2.①这组数据的众数是3;②这组数据的众数与中位数的数值不等;③这组数据的中位数与平均数的数值相等;④这组数据的平均数与众数的数值相等,其中正确的结论有(
)
A.1个
B.2个
C.3个
D.4个
10、茶叶厂用甲.乙两台包装机分装质量为400克的茶叶,从它们各自分装的茶叶中分别随机抽取10盒,测得它们实际质量的平均数和标准差分别如表所示,则包装茶叶质量较稳定的包装机为( )
A.甲
B.乙
C.甲和乙
D.无法确定
填空题
11、如果10名学生的平均身高为1.65米,其中2名学生的平均身高为1.75米,那么余下8名学生的平均身高是______米.
12、某学校举行演讲比赛,5位评委对某选手打分如下:(单位:分)9.5,9.4,9.4,9.5,9.2,则这个选手的平均分为
分.
13、一个样本的方差[(x1-3)2+(x2-3)2+…+(xn-3)2],则样本容量是______,样本平均数是______.
14、小明家去年的旅游、教育、饮食支出分别出3600元,1200元,7200元,今年这三项支出依次比去年增长10%,20%,30%,则小时家今年的总支出比去年增长的百分数是_________.
15、甲乙两地9月上旬的日平均气温如图所示,则甲乙两地这10天日平均气温方差大小关系为
(填>或<).
三、解答题
16、为了了解七、八、九年级学生的身体发育情况,有关部门从该地区的中学生中随机抽取各年级60名学生测量其身高,并对其统计制成下表(单位:cm):
年级
人数
身高(cm)
七年级
八年级
九年级
总计(频数)
143.5~153.5
12
3
0
________
153.5~163.5
18
9
6
________
163.5~173.5
24
33
39
________
173.5~183.5
6
15
12
________
183.5~193.5
0
0
3
________
(身高为整数)
(1)根据表中数据填写表中的空格;
(2)计算这些学生的平均身高.
17、某中学生为调查本校学生平均每天完成作业所用时间的情况,随机调查了50名同学,如图是根据调查所得数据绘制的统计图的一部分.
请根据以上信息,解答下列问题:
(1)将统计图补充完整;
(2)若该校共有1800名学生,根据以上调查结果估计该校全体学生平均每天完成作业所用总时间.
18、小明和小颖本学期数学平时成绩、期中成绩、期末成绩分别如下:
平时
期中
期末
小明
85
90
92
小颖
90
83
88
假如学期总评按平时成绩、期中成绩、期末成绩各占1∶3∶6的比例来计算,那么小明和小颖的学期总评成绩谁较高?
19、针对我国资源环境的具体情况,国家实行“限塑令”。“限塑令”执行前,某校为了了解本校学生所在家庭使用塑料袋的数量情况,随机调查了10名学生所在家庭每月使用塑料袋的数量,结果如下(单位:只)
65
70
85
75
79
74
91
81
95
85
(1)计算这10名学生所在家庭平均每月使用塑料袋多少只?
(2)“限塑令”执行后,家庭每月使用塑料袋数量预计将减少50%.根据上面的计算结果,估计该校1000名学生所在家庭每月使用塑料袋可减少多少只?
20、某高科技产品开发公司现有员工50名,所有员工的月工资情况如下表:
员工
管理人员
普通工作人员
人员结构
总经理
部门经理
科研人员
销售人员
高级技工
中级技工
勤杂工
员工数
1
3
2
3
24
1
每人月工资/元
21000
8400
2025
2200
1800
1600
950
请你根据上述内容,解答下列问题:
(1)该公司“高级技工”有
名;
(2)所有员工月工资的平均数为2500元,中位数为
元,众数为
元;
(3)小张到这家公司应聘普通工作人员,请你回答图中小王的问题,并指出用(2)中的哪个数据向小王介绍员工的月工资实际水平更合理些;
(4)去掉四个管理人员的工资后,请你计算出其他员工的月平均工资(结果保留整数),并判断能否反映该公司员工的月工资实际水平.
21、为了普及环保知识,增强环保意识,某中学组织了环保知识竞赛活动,初中三年级根据预选成绩选出了3名同学甲、乙、丙参加决赛,决赛要进行十次测试,三名选手的决赛成绩(满分为100分)如下表所示:
决赛成绩(单位:分)
甲
80
86
74
80
80
88
88
89
91
99
乙
85
85
87
97
85
76
88
77
87
88
丙
82
80
78
78
81
96
97
88
89
86
(1)请你填写下表:
平均数
众数
中位数
甲
85.5
87
乙
85.5
85
丙
84
(2)请从以下两个不同的角度对三个同学的决赛成绩进行分析:
①从平均数和众数相结合看,分析哪个同学成绩好些;
②从平均数和中位数相结合看,分析哪个同学成绩好些。
(3)如果在参加决赛的三名选手中选出1人参加市各中学总决赛,你认为哪个同学比较合适?并说明理由。
22、已知甲、乙两位同学11次测验成绩如图所示(单位:分):
(1)他们的平均成绩分别是多少?
(2)他们的测验成绩的方差是多少?
(3)现要从中选出一人参加比赛,历届比赛表明,成绩达到98分以上才能进入决赛,你认为应选谁参加这次比赛,为什么?
(4)分析两名同学的成绩各有何特点?并对两名同学各提一条学习建议
参考答案:
一、1、A
2、D
3、C
4、D
5、B
6、A
7、B
8、B
9、A
10、B
二、
11、1.625
12、9.4
13、12;3
14、27.3%
15、>
三、16、
年级
人数
身高(cm)
七年级
八年级
九年级
总计(频数)
143.5~153.5
12
3
0
__15__
153.5~163.5
18
9
6
__33__
163.5~173.5
24
33
39
__96__
173.5~183.5
6
15
12
__33__
183.5~193.5
0
0
3
__3__
解:(2)各组的组中值分别为148.5,158.5,168.5,178.5,188.5,=≈167(cm),即这些学生的平均身高约为167cm.
17、解:(1)50-6-12-16-8=8,补充完整的统计图如图所示.
(2)由上述统计图可得
==3(h).估计该校全体学生平均每天完成作业所用总时间为3×1800=5400(h).
18、小明
19、(1)80;
(2)4000.
20、思路建立(1)根据员工共有50人可求得高级技工的人数;
(2)根据中位数、众数的定义即可求出中位数、众数;
(3)平均数受极端值影响较大,不能代表全体员工工资的平均水平;
(4)计算后,再进行判断.
解:(1)16
(2)1700;1600
(3)这个老板的介绍不能反映该公司员工的月工资实际水平用中位数或众数来介绍更合理些.
(4)=≈1713(元),
能反映该公司员工的月工资实际水平.
21、【答案】(1)平均数:85.5;众数80,78;中位数86
(2)①∵平均数都相同,乙的众数最高,∴乙的成绩好一些;
②∵平均数都相同,甲的中位数最高,∴甲的成绩好一些.
(3)应选甲,理由是:
①中位数高说明有一半次数的分数在8以上,乙和丙达不到;
②从各次考试成绩可以看出,甲对环保知识很了解,成绩从第三次后一直在进步,说明甲平时重视环保知识,并且目前正在收集学习环保知识,他的知识面也越来越广.乙和丙后阶段成绩进步不够特出。
22、分析:对于(1)(2)根据定义及统计图中给出的数据计算即可;对于(3)应选成成绩达到98分以上的次数多的选手参加比赛;
(4)根据上面的计算结果提出建议即可.
解:(1)=×(99+100+100+95+93+90+98+100+93+90+98)=96,=×(98+99+96+94+95+92+92+98+96+99+97)=96.
即甲的平均成绩是96分,乙的平均成绩是96分.
(2)=[(99-96)2+(100-96)2+…+(98-96)2]≈14.18,
=[(98-96)2+(99-96)2+…+(97-96)2]≈5.82.
即甲的方差是14.18,乙的方差是5.82.
(3)选甲.因为11次测验中甲有4次测验成绩超过98分,而乙只有2次超过98分.
(4)由(2)(3)知乙的成绩稳定,甲的成绩波动较大,但是甲的高分率较高,有潜力.
建议:甲在今后的学习中应使成绩保持稳定,乙在今后的学习中应不断努力,提高高分率.
