2020-2021学折苏科版七年级上 册 第六章平面图形的认识(一)单元测试题(word版含答案)
文档属性
| 名称 | 2020-2021学折苏科版七年级上 册 第六章平面图形的认识(一)单元测试题(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 222.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-31 22:17:26 | ||
图片预览




文档简介
平面图形的认识(一)单元测试题
学校:________
班级:________
姓名:________
学号:________
一、单选题(共8小题)
1.如图,点A到线段BC所在直线的距离是线段( )
A.AC的长度
B.AD的长度
C.AE的长度
D.AB的长度
2.如图,佳佳从A处沿正南方向骑行到B处,再右转60°骑行到C处,然后左转80°继续骑行,此时佳佳骑行的方向为( )
A.南偏西20°
B.南偏西80°
C.南偏东20°
D.南偏东80°
3.如图所示,点A,B,C,D在同一条直线上,则图中线段的条数有( )
A.3条
B.4条
C.5条
D.6条
4.如图,经过刨平的木板上的A,B两个点,能弹出一条笔直的墨线,而且只能弹出一条墨线,能解释这一实际应用的数学知识是( )
A.点动成线
B.两点确定一条直线
C.垂线段最短
D.两点之间,线段最短
5.沿某一方向行驶的汽车经过两次拐弯后与开始行驶的方向正好相反,若汽车第一次是右拐40°,则第二次应该是( )
A.左拐40°
B.左拐50°
C.左拐140°
D.右拐140°
6.下列说法:
①两点之间的所有连线中,线段最短;
②在同一平面内,过一点有且只有一条直线与已知直线垂直;
③连接直线外一点与直线上各点的所有线段中,垂线段最短;
④直线外一点到这条直线的垂线段叫做点到直线的距离,其中正确的个数有( )
A.4个
B.3个
C.2个
D.1个
7.在同一平面内,若∠A与∠B的两边分别垂直,且∠A比∠B的3倍少40°,则∠A的度数为( )
A.20°
B.55°
C.20°或125°
D.20°或55°
8.如图所示,某公司有三个住宅区,A、B、C各区分别住有职工30人,15人,10人,且这三点在一条大道上(A,B,C三点共线),已知AB=100米,BC=200米.为了方便职工上下班,该公司的接送车打算在此间只设一个停靠点,为使所有的人步行到停靠点的路程之和最小,那么该停靠点的位置应设在( )
A.点A
B.点B
C.A,B之间
D.B,C之间
二、填空题(共8小题)
9.如图,C是线段BD的中点,AD=3,AC=7,则AB的长等于 .
10.如图,点C、D在线段AB上.AC=8cm,CD=5cm,AB=16cm,则图中所有线段的和是 cm.
11.已知A、B、C是同一直线上的三个点,且AB=9,BC=4,D是BC的中点,则AD的长是 .
12.已知∠AOB=80°,OC是过点O的一条射线,∠AOC:∠AOB=1:2,则∠BOC的度数是 .
13.计算:42°11′37″+51°49′23″= .
14.如图,直线AB、CD相交于点O,OE平分∠BOC,OF⊥OE于O,若∠AOD=78°,则∠AOF等于 .
15.如图,∠AOB=∠COD=90°,∠COE=∠BOE,OF平分∠AOD,下列结论:①∠AOE=∠DOE;②∠AOD+∠COB=180°;③∠COB﹣∠AOD=90°;④∠COE+∠BOF=180°.所有正确结论的序号是 .
16.如图,直线AB、CD相交于点O,OE平分∠BOD,OF平分∠COE.
(1)若∠AOC=76°,∠BOF= 度;
(2)若∠BOF=36°,∠AOC= 度.
三、解答题(共8小题)
17.如图,直线AB、CD相交于O,∠EOC=90°,OF是∠AOE的角平分线,∠COF=34°,求∠BOD的度数.
其中一种解题过程如下:请在括号中注明根据,在横线上补全步骤.
解:∵∠EOC=90°
∠COF=34°( )
∴∠EOF= °
∵OF是∠AOE的角平分线
∴∠AOF= =56°( )
∴∠AOC= °
∵∠AOC+ =90°
∠BOO+∠EOB=90°
∴∠BOD=∠AOC= °( )
18.如图∠AOB=120°,射线OC平分∠AOB.完成下列问题.
(1)求∠AOC和∠BOC的度数.
(2)过点O引一条射线OD,使OD与∠AOB的一边垂直,请直接写出∠COD的度数.(小于平角)
19.如图,直线AB,CD相交于点O,∠AOC=120°,OE平分∠BOC.
(1)求∠BOE的度数;
(2)若OF把∠AOE分成两个角,且∠AOF:∠EOF=2:3,判断OA是否平分∠DOF?并说明理由.
20.如图,将直角三角尺OCD的直角顶点O放在直线AB上,并且∠AOC的度数是∠BOD的度数的2倍.
(1)求∠BOD的度数;
(2)若OE,OF分别平分∠BOD,∠BOC,求∠EOF的度数.
21.如图所示,已知线段AB=4cm,BC=3cm,M,N分别是AB和BC上两点.
(1)求线段AC的长.
(2)若M为AC中点,BN=BC,求线段MN的长.
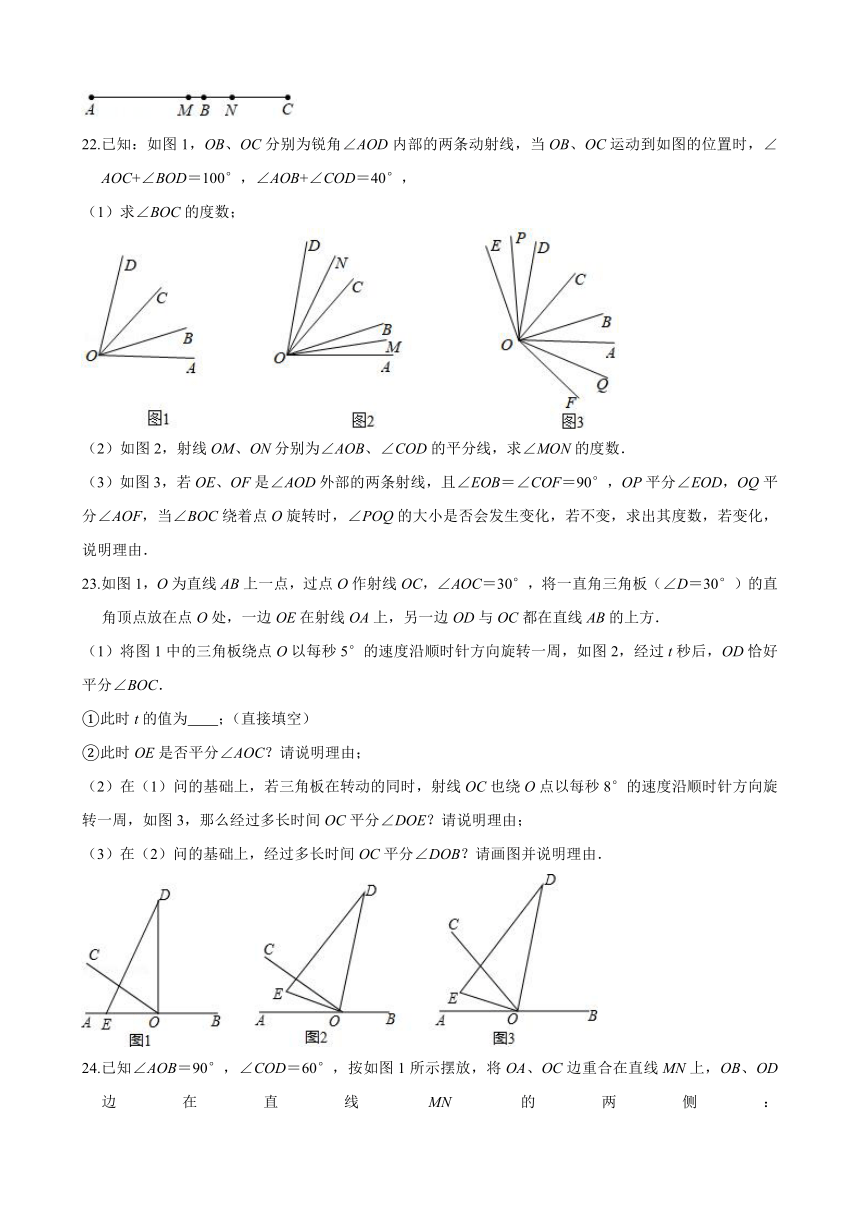
22.已知:如图1,OB、OC分别为锐角∠AOD内部的两条动射线,当OB、OC运动到如图的位置时,∠AOC+∠BOD=100°,∠AOB+∠COD=40°,
(1)求∠BOC的度数;
(2)如图2,射线OM、ON分别为∠AOB、∠COD的平分线,求∠MON的度数.
(3)如图3,若OE、OF是∠AOD外部的两条射线,且∠EOB=∠COF=90°,OP平分∠EOD,OQ平分∠AOF,当∠BOC绕着点O旋转时,∠POQ的大小是否会发生变化,若不变,求出其度数,若变化,说明理由.
23.如图1,O为直线AB上一点,过点O作射线OC,∠AOC=30°,将一直角三角板(∠D=30°)的直角顶点放在点O处,一边OE在射线OA上,另一边OD与OC都在直线AB的上方.
(1)将图1中的三角板绕点O以每秒5°的速度沿顺时针方向旋转一周,如图2,经过t秒后,OD恰好平分∠BOC.
①此时t的值为 ;(直接填空)
②此时OE是否平分∠AOC?请说明理由;
(2)在(1)问的基础上,若三角板在转动的同时,射线OC也绕O点以每秒8°的速度沿顺时针方向旋转一周,如图3,那么经过多长时间OC平分∠DOE?请说明理由;
(3)在(2)问的基础上,经过多长时间OC平分∠DOB?请画图并说明理由.
24.已知∠AOB=90°,∠COD=60°,按如图1所示摆放,将OA、OC边重合在直线MN上,OB、OD边在直线MN的两侧:
(1)保持∠AOB不动,将∠COD绕点O旋转至如图2所示的位置,则
①∠AOC+∠BOD= ;
②∠BOC﹣∠AOD= .
(2)若∠COD按每分钟5°的速度绕点O逆时针方向旋转,∠AOB按每分钟2°的速度也绕点O逆时针方向旋转,OC旋转到射线ON上时都停止运动,设旋转t分钟,计算∠MOC﹣∠AOD(用t的代数式表示).
(3)保持∠AOB不动,将∠COD绕点O逆时针方向旋转n°(n≤360),若射线OE平分∠AOC,射线OF平分∠BOD,求∠EOF的大小.
平面图形的认识(一)单元测试题
参考答案
一、单选题(共8小题)
1.【答案】
B
【解答】
解:点A到线段BC所在直线的距离是线段AD的长度,
故选:B.
2.【答案】
C
【解答】
解:过点C作DC∥AB,如图:
∵DC∥AB,∠GBH=60°,
∴∠HCF=∠GBH=60°.
∵∠HCE=80°,
∴∠ECF=∠HCE﹣∠HCF=80°﹣60°=20°,
此时佳佳骑行的方向为南偏东20°,
故选:C.
3.【答案】
D
【解答】
解:由图可得,线段有:线段AB、线段AC、线段AD、线段BC、线段BD、线段CD,共6条.
故选:D.
4.【答案】
B
【解答】
解:∵经过两点有且只有一条直线,
∴经过木板上的A、B两个点,只能弹出一条笔直的墨线.
故选:B.
5.【答案】
D
【解答】
解:依照题意画出图形,如图所示.
∵直线l1∥直线l2,
∴∠1+∠2=180°,
∴∠2=180°﹣∠1=180°﹣40°=140°,
∴∠3=∠2=140°,
∴第二次是右拐140°.
故选:D.
6.【答案】
B
【解答】
解:①两点之间的所有连线中,线段最短,说法正确;
②在同一平面内,过一点有且只有一条直线与已知直线垂直,说法正确;
③连接直线外一点与直线上各点的所有线段中,垂线段最短,说法正确;
④直线外一点到这条直线的垂线段的长度叫做点到直线的距离,说法错误.
故选:B.
7.【答案】
C
【解答】
解:设∠B是x度,根据题意,得
①两个角相等时,如图1:
∠B=∠A=x°,
x=3x﹣40
解得,x=20,
故∠A=20°,
②两个角互补时,如图2:
x+3x﹣40=180,
所以x=55,
3×55°﹣40°=125°
故∠A的度数为:20°或125°.
故选:C.
8.【答案】
A
【解答】
解:①以点A为停靠点,则所有人的路程的和=15×100+10×300=4500(米),
②以点B为停靠点,则所有人的路程的和=30×100+10×200=5000(米),
③以点C为停靠点,则所有人的路程的和=30×300+15×200=12000(米),
④当在AB之间停靠时,设停靠点到A的距离是m,则(0<m<100),则所有人的路程的和是:30m+15(100﹣m)+10(300﹣m)=4500+5m>4500,
⑤当在BC之间停靠时,设停靠点到B的距离为n,则(0<n<200),则总路程为30(100+n)+15n+10(200﹣n)=5000+35n>4500.
∴该停靠点的位置应设在点A;
故选:A.
二、填空题(共8小题)
9.【答案】
11
【解答】
解:∵AD=3,AC=7∴CD=4.
∵点C是线段BD的中点∴BD=2CD=8
AB=BD+AD=3+8=11.故应填11.
10.【答案】
53
【解答】
解:图中线段有AC、AD、AB、CD、CB、DB,共六条线段.
其中AC=8cm,
∴AD=AC+CD=8+5=13(cm),
∴AB=16cm,CD=5cm,
∴CB=AB﹣AC=16﹣8=8(cm),
∴DB=AB﹣AC﹣CD=16﹣8﹣5=3(cm),
故图中所有线段的和为53cm,
故答案为:53.
11.【答案】
11或7
【解答】
解:当点C在线段AB之间时,
∵AB=9,BC=4,
D是BC的中点,
∴CD=2,
∴AD=7,
当C在AB的延长线上的时候,
BD=2,
∴AD=AB+BD,
=9+2,
=11.
故答案为:11或7.
12.【答案】
40°或120°
【解答】
解:分两种情况讨论,
情况一:如图1,
∵∠AOB=80°,∠AOC:∠AOB=1:2,
∴∠AOC=40°,
∴∠BOC=∠AOB+∠AOC=80°+40°=120°;
情况二:如图2,
∵∠AOB=80°,∠AOC:∠AOB=1:2,
∴∠AOC=40°,
∴∠BOC=∠AOB﹣∠AOC=80°﹣40°=40°;
综上所述,∠BOC的度数是120°或40°,
故答案为:120°或40°.
13.【答案】
94°1′
【解答】
解:42°11′37″+51°49′23″=93°60′60″=94°1′.
故答案为:94°1′.
14.【答案】
51°
【解答】
解:∵∠BOC=∠AOD=78°,OE平分∠BOC,
∴∠BOE=∠BOC=39°.
∵OF⊥OE,
∴∠EOF=90°.
∴∠AOF=180°﹣∠EOF﹣∠BOE=180°﹣90°﹣39°=51°.
故答案为:51°.
15.【答案】
①②④
【解答】
解:∵∠AOB=∠COD=90°,
∴∠AOC=∠BOD,
而∠COE=∠BOE,
∴∠AOE=∠DOE,所以①正确;
∠AOD+∠COB=∠AOD+∠AOC+90°=90°+90°=180°,所以②正确;
∠COB﹣∠AOD=∠AOC+90°﹣∠AOD,
而∠AOC≠∠AOD,所以③不正确;
∵OF平分∠AOD,
∴∠AOF=∠DOF,
而∠AOE=∠DOE,
∴∠AOF+∠AOE=∠DOF+∠DOE=180°,即点F、O、E共线,
∵∠COE=∠BOE,
∴∠COE+∠BOF=180°,所以④正确.
故答案为:①②④.
16.【答案】
【第1空】33
【第2空】72
【解答】
解:(1)∵∠DOB和∠AOC是对顶角,
∴∠DOB=∠AOC=76°,
∵OE平分∠BOD,
∴∠DOE=∠EOB=∠DOB=38°,
∴∠COE=180°﹣∠DOE=142°,
∵OF平分∠COE,
∴∠COF=∠FOE=∠COE=71°,
∴∠BOF=∠FOE﹣∠EOB=33°.
故答案为33°.
(2))∵∠DOB和∠AOC是对顶角,
∴∠DOB=∠AOC,
∵OE平分∠BOD,
∴∠DOE=∠EOB=∠DOB,
∵OF平分∠COE,
∴∠COF=∠FOE=∠COE,
∵∠AOC=180°﹣∠COF﹣∠BOF
=180°﹣(∠EOB+∠BOF)﹣∠BOF
=108°﹣∠EOB
=108°﹣∠AOC
∴∠AOC=72°.
故答案为72°.
三、解答题(共8小题)
17.【答案】
【第1空】已知
【第2空】56
【第3空】∠EOF
【第4空】角平分线的定义
【第5空】22
【第6空】∠EOB
【第7空】22
【第8空】同角的余角相等
【解答】
解:∵∠EOC=90°,
∠COF=34°(已知),
∴∠EOF=56°,
∵OF是∠AOE的角平分线,
∴∠AOF=∠EOF=56°(角平分线的定义),
∴∠AOC=22°,
∵∠AOC+∠EOB=90°,
∠BOO+∠EOB=90°,
∴∠BOD=∠AOC=22°(同角的余角相等),
故答案为:已知;56;∠EOF;角平分线的定义;22;∠EOB;同角的余角相等.
18.【解答】
解:(1)∵∠AOB=120°,射线OC平分∠AOB,
∴∠AOC=∠BOC==60°;
(2)如图,当OD⊥OA时,
∠COD=90°﹣∠AOC=30°或∠COD=90°+∠AOC=150°;
同理,当OD⊥OB时,∠COD=90°﹣∠BOC=30°或∠COD=90°+∠BOC=150°;
故∠COD的度数为30°或150°.
19.【解答】
解:(1)∵∠AOC=120°,
∴∠BOC=180°﹣120°=60°,
∵OE平分∠BOC,
∴∠BOE=∠BOC=×60°=30°;
(2)OA平分∠DOF,
理由如下:∵∠BOE=30°,
∴∠AOE=180°﹣30°=150°,
∵∠AOF:∠EOF=2:3,
∴∠AOF=60°,∠EOF=90°,
∵∠AOD=∠BOC=60°,
∴∠AOD=∠AOF,
∴OA平分∠DOF.
20.【解答】
解:(1)∵∠COD=90°,∠AOC+∠COD+∠BOD=180°,
∴∠AOC+∠BOD=90°,
∵∠AOC的度数是∠BOD的度数的2倍,
∴∠AOC=2∠BOD,
∴2∠BOD+∠BOD=90°,
∴∠BOD=30°;
(2)由题意得,∠BOC=∠BOD+∠COD=30°+90°=120°,
∵OE,OF分别平分∠BOD,∠BOC,
∴∠BOF=∠BOC=60°,∠BOE=∠BOD=15°,
∴∠EOF=∠BOF﹣∠BOE=45°.
21.【解答】
解:(1)∵AB=4cm,BC=3cm,
∴AC=AB+BC=7(cm);
(2)∵AC=7cm,M为AC中点,
∴CM=AC=7=(cm),
∵BN=BC,
∴BN=3=1(cm),
∴CN=BC﹣BN=2(cm),
∴MN=CM﹣CN=﹣2=(cm).
22.【解答】
解:(1)∵∠AOC+∠BOD=100°,
∴∠AOB+∠BOC+∠BOC+∠COD=100°,
又∵∠AOB+∠COD=40°,
∴2∠BOC=100°﹣40°=60°,
∴∠BOC=30°,
答:∠BOC的度数为30°;
(2)∵OM是∠AOB的平分线,
∴∠AOM=∠BOM=∠AOB,
又∵ON是∠COD的平分线,
∴∠CON=∠DON=∠COD,
∴∠DON+∠BOM=(∠COD+∠AOB)=×40°=20°,
∴∠MON=∠BOM+∠BOC+∠DON=20°+30°=50°,
答:∠MON的度数为50°;
(3)∵∠EOB=∠COF=90°,∠BOC=30°,
∴∠EOF=90°+90°﹣30°=150°,
∵∠AOD=∠AOB+∠BOC+∠COD=40°+30°=70°,
∴∠AOF+∠DOE=∠EOF﹣∠AOD=150°﹣70°=80°,
又∵OP平分∠EOD,OQ平分∠AOF,
∴∠AOQ=∠FOQ=∠AOF,∠DOP=∠EOP=∠DOE,
∴∠AOQ+∠DOP=(∠AOF+∠DOE)=×80°=40°,
∴∠POQ=∠AOQ+∠DOP+∠AOD=40°+70°=110°.
23.【答案】
3
【解答】
解:(1)①∵∠AOC=30°,∠AOB=180°,
∴∠BOC=∠AOB﹣∠AOC=150°,
∵OD平分∠BOC,
∴∠BOD=BOC=75°,
∴t==3.
②是,理由如下:
∵转动3秒,∴∠AOE=15°,
∴∠COE=∠AOC﹣∠AOE=15°,
∴∠COE=∠AOE,
即OE平分∠AOC.
(2)三角板旋转一周所需的时间为==72(秒),射线OC绕O点旋转一周所需的时间为=45(秒),
设经过x秒时,OC平分∠DOE,
由题意:①8x﹣5x=45﹣30,
解得:x=5,
②8x﹣5x=360﹣30+45,
解得:x=125>45,不合题意,
③∵射线OC绕O点旋转一周所需的时间为=45(秒),45秒后停止运动,
∴OE旋转345°时,OC平分∠DOE,
∴t==69(秒),
综上所述,t=5秒或69秒时,OC平分∠DOE.
(3)如图3中,由题意可知,OD旋转到与OB重合时,需要90÷5=18(秒),OC旋转到与OB重合时,需要(180﹣30)÷8=18(秒),
所以OD比OC早与OB重合,
设经过x秒时,OC平分∠DOB,
由题意:8x﹣(180﹣30)=(5x﹣90),
解得:x=,
所以经秒时,OC平分∠DOB.
24.【答案】
【第1空】150°
【第2空】30°
【解答】
解:(1)①∠AOC+∠BOD
=∠AOC+∠AOD+∠AOB
=∠COD+∠AOB
=60°+90°
=150°;
②∠BOC﹣∠AOD
=(∠AOB﹣∠AOC)﹣(∠COD﹣∠AOC)
=∠AOB﹣∠AOC﹣∠COD+∠AOC
=∠AOB﹣∠COD
=90°﹣60°
=30°;
故答案为:150°、30°;
(2)设运动时间为t秒,0<t≤36,∠MOC=(5t)°,
①0<t≤20时,OD与OA相遇前,∠AOD=(60+2t﹣5t)°=(60﹣3t)°,
∴∠MOC﹣∠AOD=(8t﹣60)°;
②20<t≤36时,OD与OA相遇后,∠AOD=[5t﹣(60+2t)]°=(3t﹣60)°,
∴∠MOC﹣∠AOD=(2t+60)°;
(3)设OC绕点O逆时针旋转n°,则OD也绕点O逆时针旋转n°,
①0<n°≤150°时,如图4,
射线OE、OF在射线OB同侧,在直线MN同侧,
∵∠BOF=[90°﹣(n﹣60°)]=(150﹣n)°,∠BOE=(90﹣n)°=(180﹣n)°,
∴∠EOF=∠BOE﹣∠BOF=15°;
②150°<n°≤180°时,如图5,
射线OE、OF在射线OB异侧,在直线MN同侧,
∵°,∠BOE=(90﹣n)°=(180﹣n)°,
∴∠EOF=∠BOE+∠BOF=15°;
③180°<n°≤330°时,如图6,
射线OE、OF在射线OB异侧,在直线MN异侧,
∵°,°,
∴∠EOF=∠DOF+∠COD+∠COE=165°;
④330°<n°≤360°时,如图7,
射线OE、OF在射线OB同侧,在直线MN异侧,
∵∠DOF=[360﹣(n﹣150)]°=(510﹣n)°,°,
∴∠EOF=∠DOF﹣∠COD﹣∠COE=15°;
综上,∠EOF=15°或165°.
学校:________
班级:________
姓名:________
学号:________
一、单选题(共8小题)
1.如图,点A到线段BC所在直线的距离是线段( )
A.AC的长度
B.AD的长度
C.AE的长度
D.AB的长度
2.如图,佳佳从A处沿正南方向骑行到B处,再右转60°骑行到C处,然后左转80°继续骑行,此时佳佳骑行的方向为( )
A.南偏西20°
B.南偏西80°
C.南偏东20°
D.南偏东80°
3.如图所示,点A,B,C,D在同一条直线上,则图中线段的条数有( )
A.3条
B.4条
C.5条
D.6条
4.如图,经过刨平的木板上的A,B两个点,能弹出一条笔直的墨线,而且只能弹出一条墨线,能解释这一实际应用的数学知识是( )
A.点动成线
B.两点确定一条直线
C.垂线段最短
D.两点之间,线段最短
5.沿某一方向行驶的汽车经过两次拐弯后与开始行驶的方向正好相反,若汽车第一次是右拐40°,则第二次应该是( )
A.左拐40°
B.左拐50°
C.左拐140°
D.右拐140°
6.下列说法:
①两点之间的所有连线中,线段最短;
②在同一平面内,过一点有且只有一条直线与已知直线垂直;
③连接直线外一点与直线上各点的所有线段中,垂线段最短;
④直线外一点到这条直线的垂线段叫做点到直线的距离,其中正确的个数有( )
A.4个
B.3个
C.2个
D.1个
7.在同一平面内,若∠A与∠B的两边分别垂直,且∠A比∠B的3倍少40°,则∠A的度数为( )
A.20°
B.55°
C.20°或125°
D.20°或55°
8.如图所示,某公司有三个住宅区,A、B、C各区分别住有职工30人,15人,10人,且这三点在一条大道上(A,B,C三点共线),已知AB=100米,BC=200米.为了方便职工上下班,该公司的接送车打算在此间只设一个停靠点,为使所有的人步行到停靠点的路程之和最小,那么该停靠点的位置应设在( )
A.点A
B.点B
C.A,B之间
D.B,C之间
二、填空题(共8小题)
9.如图,C是线段BD的中点,AD=3,AC=7,则AB的长等于 .
10.如图,点C、D在线段AB上.AC=8cm,CD=5cm,AB=16cm,则图中所有线段的和是 cm.
11.已知A、B、C是同一直线上的三个点,且AB=9,BC=4,D是BC的中点,则AD的长是 .
12.已知∠AOB=80°,OC是过点O的一条射线,∠AOC:∠AOB=1:2,则∠BOC的度数是 .
13.计算:42°11′37″+51°49′23″= .
14.如图,直线AB、CD相交于点O,OE平分∠BOC,OF⊥OE于O,若∠AOD=78°,则∠AOF等于 .
15.如图,∠AOB=∠COD=90°,∠COE=∠BOE,OF平分∠AOD,下列结论:①∠AOE=∠DOE;②∠AOD+∠COB=180°;③∠COB﹣∠AOD=90°;④∠COE+∠BOF=180°.所有正确结论的序号是 .
16.如图,直线AB、CD相交于点O,OE平分∠BOD,OF平分∠COE.
(1)若∠AOC=76°,∠BOF= 度;
(2)若∠BOF=36°,∠AOC= 度.
三、解答题(共8小题)
17.如图,直线AB、CD相交于O,∠EOC=90°,OF是∠AOE的角平分线,∠COF=34°,求∠BOD的度数.
其中一种解题过程如下:请在括号中注明根据,在横线上补全步骤.
解:∵∠EOC=90°
∠COF=34°( )
∴∠EOF= °
∵OF是∠AOE的角平分线
∴∠AOF= =56°( )
∴∠AOC= °
∵∠AOC+ =90°
∠BOO+∠EOB=90°
∴∠BOD=∠AOC= °( )
18.如图∠AOB=120°,射线OC平分∠AOB.完成下列问题.
(1)求∠AOC和∠BOC的度数.
(2)过点O引一条射线OD,使OD与∠AOB的一边垂直,请直接写出∠COD的度数.(小于平角)
19.如图,直线AB,CD相交于点O,∠AOC=120°,OE平分∠BOC.
(1)求∠BOE的度数;
(2)若OF把∠AOE分成两个角,且∠AOF:∠EOF=2:3,判断OA是否平分∠DOF?并说明理由.
20.如图,将直角三角尺OCD的直角顶点O放在直线AB上,并且∠AOC的度数是∠BOD的度数的2倍.
(1)求∠BOD的度数;
(2)若OE,OF分别平分∠BOD,∠BOC,求∠EOF的度数.
21.如图所示,已知线段AB=4cm,BC=3cm,M,N分别是AB和BC上两点.
(1)求线段AC的长.
(2)若M为AC中点,BN=BC,求线段MN的长.
22.已知:如图1,OB、OC分别为锐角∠AOD内部的两条动射线,当OB、OC运动到如图的位置时,∠AOC+∠BOD=100°,∠AOB+∠COD=40°,
(1)求∠BOC的度数;
(2)如图2,射线OM、ON分别为∠AOB、∠COD的平分线,求∠MON的度数.
(3)如图3,若OE、OF是∠AOD外部的两条射线,且∠EOB=∠COF=90°,OP平分∠EOD,OQ平分∠AOF,当∠BOC绕着点O旋转时,∠POQ的大小是否会发生变化,若不变,求出其度数,若变化,说明理由.
23.如图1,O为直线AB上一点,过点O作射线OC,∠AOC=30°,将一直角三角板(∠D=30°)的直角顶点放在点O处,一边OE在射线OA上,另一边OD与OC都在直线AB的上方.
(1)将图1中的三角板绕点O以每秒5°的速度沿顺时针方向旋转一周,如图2,经过t秒后,OD恰好平分∠BOC.
①此时t的值为 ;(直接填空)
②此时OE是否平分∠AOC?请说明理由;
(2)在(1)问的基础上,若三角板在转动的同时,射线OC也绕O点以每秒8°的速度沿顺时针方向旋转一周,如图3,那么经过多长时间OC平分∠DOE?请说明理由;
(3)在(2)问的基础上,经过多长时间OC平分∠DOB?请画图并说明理由.
24.已知∠AOB=90°,∠COD=60°,按如图1所示摆放,将OA、OC边重合在直线MN上,OB、OD边在直线MN的两侧:
(1)保持∠AOB不动,将∠COD绕点O旋转至如图2所示的位置,则
①∠AOC+∠BOD= ;
②∠BOC﹣∠AOD= .
(2)若∠COD按每分钟5°的速度绕点O逆时针方向旋转,∠AOB按每分钟2°的速度也绕点O逆时针方向旋转,OC旋转到射线ON上时都停止运动,设旋转t分钟,计算∠MOC﹣∠AOD(用t的代数式表示).
(3)保持∠AOB不动,将∠COD绕点O逆时针方向旋转n°(n≤360),若射线OE平分∠AOC,射线OF平分∠BOD,求∠EOF的大小.
平面图形的认识(一)单元测试题
参考答案
一、单选题(共8小题)
1.【答案】
B
【解答】
解:点A到线段BC所在直线的距离是线段AD的长度,
故选:B.
2.【答案】
C
【解答】
解:过点C作DC∥AB,如图:
∵DC∥AB,∠GBH=60°,
∴∠HCF=∠GBH=60°.
∵∠HCE=80°,
∴∠ECF=∠HCE﹣∠HCF=80°﹣60°=20°,
此时佳佳骑行的方向为南偏东20°,
故选:C.
3.【答案】
D
【解答】
解:由图可得,线段有:线段AB、线段AC、线段AD、线段BC、线段BD、线段CD,共6条.
故选:D.
4.【答案】
B
【解答】
解:∵经过两点有且只有一条直线,
∴经过木板上的A、B两个点,只能弹出一条笔直的墨线.
故选:B.
5.【答案】
D
【解答】
解:依照题意画出图形,如图所示.
∵直线l1∥直线l2,
∴∠1+∠2=180°,
∴∠2=180°﹣∠1=180°﹣40°=140°,
∴∠3=∠2=140°,
∴第二次是右拐140°.
故选:D.
6.【答案】
B
【解答】
解:①两点之间的所有连线中,线段最短,说法正确;
②在同一平面内,过一点有且只有一条直线与已知直线垂直,说法正确;
③连接直线外一点与直线上各点的所有线段中,垂线段最短,说法正确;
④直线外一点到这条直线的垂线段的长度叫做点到直线的距离,说法错误.
故选:B.
7.【答案】
C
【解答】
解:设∠B是x度,根据题意,得
①两个角相等时,如图1:
∠B=∠A=x°,
x=3x﹣40
解得,x=20,
故∠A=20°,
②两个角互补时,如图2:
x+3x﹣40=180,
所以x=55,
3×55°﹣40°=125°
故∠A的度数为:20°或125°.
故选:C.
8.【答案】
A
【解答】
解:①以点A为停靠点,则所有人的路程的和=15×100+10×300=4500(米),
②以点B为停靠点,则所有人的路程的和=30×100+10×200=5000(米),
③以点C为停靠点,则所有人的路程的和=30×300+15×200=12000(米),
④当在AB之间停靠时,设停靠点到A的距离是m,则(0<m<100),则所有人的路程的和是:30m+15(100﹣m)+10(300﹣m)=4500+5m>4500,
⑤当在BC之间停靠时,设停靠点到B的距离为n,则(0<n<200),则总路程为30(100+n)+15n+10(200﹣n)=5000+35n>4500.
∴该停靠点的位置应设在点A;
故选:A.
二、填空题(共8小题)
9.【答案】
11
【解答】
解:∵AD=3,AC=7∴CD=4.
∵点C是线段BD的中点∴BD=2CD=8
AB=BD+AD=3+8=11.故应填11.
10.【答案】
53
【解答】
解:图中线段有AC、AD、AB、CD、CB、DB,共六条线段.
其中AC=8cm,
∴AD=AC+CD=8+5=13(cm),
∴AB=16cm,CD=5cm,
∴CB=AB﹣AC=16﹣8=8(cm),
∴DB=AB﹣AC﹣CD=16﹣8﹣5=3(cm),
故图中所有线段的和为53cm,
故答案为:53.
11.【答案】
11或7
【解答】
解:当点C在线段AB之间时,
∵AB=9,BC=4,
D是BC的中点,
∴CD=2,
∴AD=7,
当C在AB的延长线上的时候,
BD=2,
∴AD=AB+BD,
=9+2,
=11.
故答案为:11或7.
12.【答案】
40°或120°
【解答】
解:分两种情况讨论,
情况一:如图1,
∵∠AOB=80°,∠AOC:∠AOB=1:2,
∴∠AOC=40°,
∴∠BOC=∠AOB+∠AOC=80°+40°=120°;
情况二:如图2,
∵∠AOB=80°,∠AOC:∠AOB=1:2,
∴∠AOC=40°,
∴∠BOC=∠AOB﹣∠AOC=80°﹣40°=40°;
综上所述,∠BOC的度数是120°或40°,
故答案为:120°或40°.
13.【答案】
94°1′
【解答】
解:42°11′37″+51°49′23″=93°60′60″=94°1′.
故答案为:94°1′.
14.【答案】
51°
【解答】
解:∵∠BOC=∠AOD=78°,OE平分∠BOC,
∴∠BOE=∠BOC=39°.
∵OF⊥OE,
∴∠EOF=90°.
∴∠AOF=180°﹣∠EOF﹣∠BOE=180°﹣90°﹣39°=51°.
故答案为:51°.
15.【答案】
①②④
【解答】
解:∵∠AOB=∠COD=90°,
∴∠AOC=∠BOD,
而∠COE=∠BOE,
∴∠AOE=∠DOE,所以①正确;
∠AOD+∠COB=∠AOD+∠AOC+90°=90°+90°=180°,所以②正确;
∠COB﹣∠AOD=∠AOC+90°﹣∠AOD,
而∠AOC≠∠AOD,所以③不正确;
∵OF平分∠AOD,
∴∠AOF=∠DOF,
而∠AOE=∠DOE,
∴∠AOF+∠AOE=∠DOF+∠DOE=180°,即点F、O、E共线,
∵∠COE=∠BOE,
∴∠COE+∠BOF=180°,所以④正确.
故答案为:①②④.
16.【答案】
【第1空】33
【第2空】72
【解答】
解:(1)∵∠DOB和∠AOC是对顶角,
∴∠DOB=∠AOC=76°,
∵OE平分∠BOD,
∴∠DOE=∠EOB=∠DOB=38°,
∴∠COE=180°﹣∠DOE=142°,
∵OF平分∠COE,
∴∠COF=∠FOE=∠COE=71°,
∴∠BOF=∠FOE﹣∠EOB=33°.
故答案为33°.
(2))∵∠DOB和∠AOC是对顶角,
∴∠DOB=∠AOC,
∵OE平分∠BOD,
∴∠DOE=∠EOB=∠DOB,
∵OF平分∠COE,
∴∠COF=∠FOE=∠COE,
∵∠AOC=180°﹣∠COF﹣∠BOF
=180°﹣(∠EOB+∠BOF)﹣∠BOF
=108°﹣∠EOB
=108°﹣∠AOC
∴∠AOC=72°.
故答案为72°.
三、解答题(共8小题)
17.【答案】
【第1空】已知
【第2空】56
【第3空】∠EOF
【第4空】角平分线的定义
【第5空】22
【第6空】∠EOB
【第7空】22
【第8空】同角的余角相等
【解答】
解:∵∠EOC=90°,
∠COF=34°(已知),
∴∠EOF=56°,
∵OF是∠AOE的角平分线,
∴∠AOF=∠EOF=56°(角平分线的定义),
∴∠AOC=22°,
∵∠AOC+∠EOB=90°,
∠BOO+∠EOB=90°,
∴∠BOD=∠AOC=22°(同角的余角相等),
故答案为:已知;56;∠EOF;角平分线的定义;22;∠EOB;同角的余角相等.
18.【解答】
解:(1)∵∠AOB=120°,射线OC平分∠AOB,
∴∠AOC=∠BOC==60°;
(2)如图,当OD⊥OA时,
∠COD=90°﹣∠AOC=30°或∠COD=90°+∠AOC=150°;
同理,当OD⊥OB时,∠COD=90°﹣∠BOC=30°或∠COD=90°+∠BOC=150°;
故∠COD的度数为30°或150°.
19.【解答】
解:(1)∵∠AOC=120°,
∴∠BOC=180°﹣120°=60°,
∵OE平分∠BOC,
∴∠BOE=∠BOC=×60°=30°;
(2)OA平分∠DOF,
理由如下:∵∠BOE=30°,
∴∠AOE=180°﹣30°=150°,
∵∠AOF:∠EOF=2:3,
∴∠AOF=60°,∠EOF=90°,
∵∠AOD=∠BOC=60°,
∴∠AOD=∠AOF,
∴OA平分∠DOF.
20.【解答】
解:(1)∵∠COD=90°,∠AOC+∠COD+∠BOD=180°,
∴∠AOC+∠BOD=90°,
∵∠AOC的度数是∠BOD的度数的2倍,
∴∠AOC=2∠BOD,
∴2∠BOD+∠BOD=90°,
∴∠BOD=30°;
(2)由题意得,∠BOC=∠BOD+∠COD=30°+90°=120°,
∵OE,OF分别平分∠BOD,∠BOC,
∴∠BOF=∠BOC=60°,∠BOE=∠BOD=15°,
∴∠EOF=∠BOF﹣∠BOE=45°.
21.【解答】
解:(1)∵AB=4cm,BC=3cm,
∴AC=AB+BC=7(cm);
(2)∵AC=7cm,M为AC中点,
∴CM=AC=7=(cm),
∵BN=BC,
∴BN=3=1(cm),
∴CN=BC﹣BN=2(cm),
∴MN=CM﹣CN=﹣2=(cm).
22.【解答】
解:(1)∵∠AOC+∠BOD=100°,
∴∠AOB+∠BOC+∠BOC+∠COD=100°,
又∵∠AOB+∠COD=40°,
∴2∠BOC=100°﹣40°=60°,
∴∠BOC=30°,
答:∠BOC的度数为30°;
(2)∵OM是∠AOB的平分线,
∴∠AOM=∠BOM=∠AOB,
又∵ON是∠COD的平分线,
∴∠CON=∠DON=∠COD,
∴∠DON+∠BOM=(∠COD+∠AOB)=×40°=20°,
∴∠MON=∠BOM+∠BOC+∠DON=20°+30°=50°,
答:∠MON的度数为50°;
(3)∵∠EOB=∠COF=90°,∠BOC=30°,
∴∠EOF=90°+90°﹣30°=150°,
∵∠AOD=∠AOB+∠BOC+∠COD=40°+30°=70°,
∴∠AOF+∠DOE=∠EOF﹣∠AOD=150°﹣70°=80°,
又∵OP平分∠EOD,OQ平分∠AOF,
∴∠AOQ=∠FOQ=∠AOF,∠DOP=∠EOP=∠DOE,
∴∠AOQ+∠DOP=(∠AOF+∠DOE)=×80°=40°,
∴∠POQ=∠AOQ+∠DOP+∠AOD=40°+70°=110°.
23.【答案】
3
【解答】
解:(1)①∵∠AOC=30°,∠AOB=180°,
∴∠BOC=∠AOB﹣∠AOC=150°,
∵OD平分∠BOC,
∴∠BOD=BOC=75°,
∴t==3.
②是,理由如下:
∵转动3秒,∴∠AOE=15°,
∴∠COE=∠AOC﹣∠AOE=15°,
∴∠COE=∠AOE,
即OE平分∠AOC.
(2)三角板旋转一周所需的时间为==72(秒),射线OC绕O点旋转一周所需的时间为=45(秒),
设经过x秒时,OC平分∠DOE,
由题意:①8x﹣5x=45﹣30,
解得:x=5,
②8x﹣5x=360﹣30+45,
解得:x=125>45,不合题意,
③∵射线OC绕O点旋转一周所需的时间为=45(秒),45秒后停止运动,
∴OE旋转345°时,OC平分∠DOE,
∴t==69(秒),
综上所述,t=5秒或69秒时,OC平分∠DOE.
(3)如图3中,由题意可知,OD旋转到与OB重合时,需要90÷5=18(秒),OC旋转到与OB重合时,需要(180﹣30)÷8=18(秒),
所以OD比OC早与OB重合,
设经过x秒时,OC平分∠DOB,
由题意:8x﹣(180﹣30)=(5x﹣90),
解得:x=,
所以经秒时,OC平分∠DOB.
24.【答案】
【第1空】150°
【第2空】30°
【解答】
解:(1)①∠AOC+∠BOD
=∠AOC+∠AOD+∠AOB
=∠COD+∠AOB
=60°+90°
=150°;
②∠BOC﹣∠AOD
=(∠AOB﹣∠AOC)﹣(∠COD﹣∠AOC)
=∠AOB﹣∠AOC﹣∠COD+∠AOC
=∠AOB﹣∠COD
=90°﹣60°
=30°;
故答案为:150°、30°;
(2)设运动时间为t秒,0<t≤36,∠MOC=(5t)°,
①0<t≤20时,OD与OA相遇前,∠AOD=(60+2t﹣5t)°=(60﹣3t)°,
∴∠MOC﹣∠AOD=(8t﹣60)°;
②20<t≤36时,OD与OA相遇后,∠AOD=[5t﹣(60+2t)]°=(3t﹣60)°,
∴∠MOC﹣∠AOD=(2t+60)°;
(3)设OC绕点O逆时针旋转n°,则OD也绕点O逆时针旋转n°,
①0<n°≤150°时,如图4,
射线OE、OF在射线OB同侧,在直线MN同侧,
∵∠BOF=[90°﹣(n﹣60°)]=(150﹣n)°,∠BOE=(90﹣n)°=(180﹣n)°,
∴∠EOF=∠BOE﹣∠BOF=15°;
②150°<n°≤180°时,如图5,
射线OE、OF在射线OB异侧,在直线MN同侧,
∵°,∠BOE=(90﹣n)°=(180﹣n)°,
∴∠EOF=∠BOE+∠BOF=15°;
③180°<n°≤330°时,如图6,
射线OE、OF在射线OB异侧,在直线MN异侧,
∵°,°,
∴∠EOF=∠DOF+∠COD+∠COE=165°;
④330°<n°≤360°时,如图7,
射线OE、OF在射线OB同侧,在直线MN异侧,
∵∠DOF=[360﹣(n﹣150)]°=(510﹣n)°,°,
∴∠EOF=∠DOF﹣∠COD﹣∠COE=15°;
综上,∠EOF=15°或165°.
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
