2020-2021学年 人教版(五四制)七年级数学下册 第17章 三角形 单元检测试题(word版含解析)
文档属性
| 名称 | 2020-2021学年 人教版(五四制)七年级数学下册 第17章 三角形 单元检测试题(word版含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 128.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-01 00:00:00 | ||
图片预览




文档简介
2020-2021学年七年级数学人教版(五四制)下册
第17章
三角形
单元检测试题
一、选择题(每小题4分,共40分)
1.若一个三角形的三个内角互不相等,则它的最小角必小于( )
A.45°
B.60°
C.30°
D.90°
2.下列命题中,不正确的为( )
A.钝角三角形是斜三角形
B.在一个三角形中至多有一个内角不小于60o
C.三角形的没有公共顶点的两个外角的和大于平角
D.三角形的外角中,最小的一个是钝角,那它一定是锐角三角形
3.以下命题正确的是( )
A.三角形三个外角的和是360o
B.三角形一个外角大于它的两个内角的和
C.三角形的外角都不大于90o
D.三角形中的内角没有大于120o的
4.下列说法正确的是( )
A.一个钝角三角形一定不是等腰三角形,也不是等边三角形
B.一个等腰三角形一定是锐角三角形,或直角三角形
C.一个直角三角形一定不是等腰三角形,也不是等边三角形
D.一个等边三角形一定不是钝角三角形,也不是直角三角形
5.在三角形的三个外角(一个顶点只取一个外角)中,钝角的个数至少是( )
A.3
B.2
C.1
D.0
6.如图,△ABC中,AD是BC边上中线,AE是BD边的中线,AF是DC边的中线,且AB<AC,则下列结论中错误的是( )
A.∠1>∠2>∠3>∠C
B.BE=ED=DF=FC
C.∠1>∠4+∠5+∠C
D.AE=AF
7.锐角三角形中任意两个锐角的和必大于( )
A.120°
B.110°
C.100°
D.90°
8.如图,在△ADE中,引线段EB与EC,下列各等式中,正确的是( )
A.∠A+∠1+∠7=∠D+∠3+∠6
B.∠1+∠5=∠2+∠7
C.∠6+∠A=∠2+∠7
D.∠A+∠5+∠7=∠2+∠8+∠6
9.若一个三角形三个外角的度数之比为2:3:4,则与之对应的三个内角的度数的比为( )
A.5:3:1
B.3:2:4
C.4:3:2
D.3:1:5
10.如图所示,已知∠1=60°,∠A+∠B+∠C+∠D+∠E+∠F=( )
A.180°
B.360°
C.240°
D.200°
二、填空题(每小题4分,共24分)
11.在△ABC中,∠A是∠B的2倍,∠C比∠A+∠B还大12°,则这个三角形是
三角形.
12.一个三角形中,最少有
个锐角.
13.三角形中最大角α的范围为
,最小角β的范围是
.
14.在△ABC中,∠A=∠B=∠C,则∠A=
,∠B=
,∠C=
.此三角形为
三角形.
15.在△ABC中,∠A:∠B:∠C=3:5:10,则∠B等于
.
16.在△ABC中,若∠A+∠C=2∠B,最小角为30o,则最大角为
.
三、解答题(共36分)
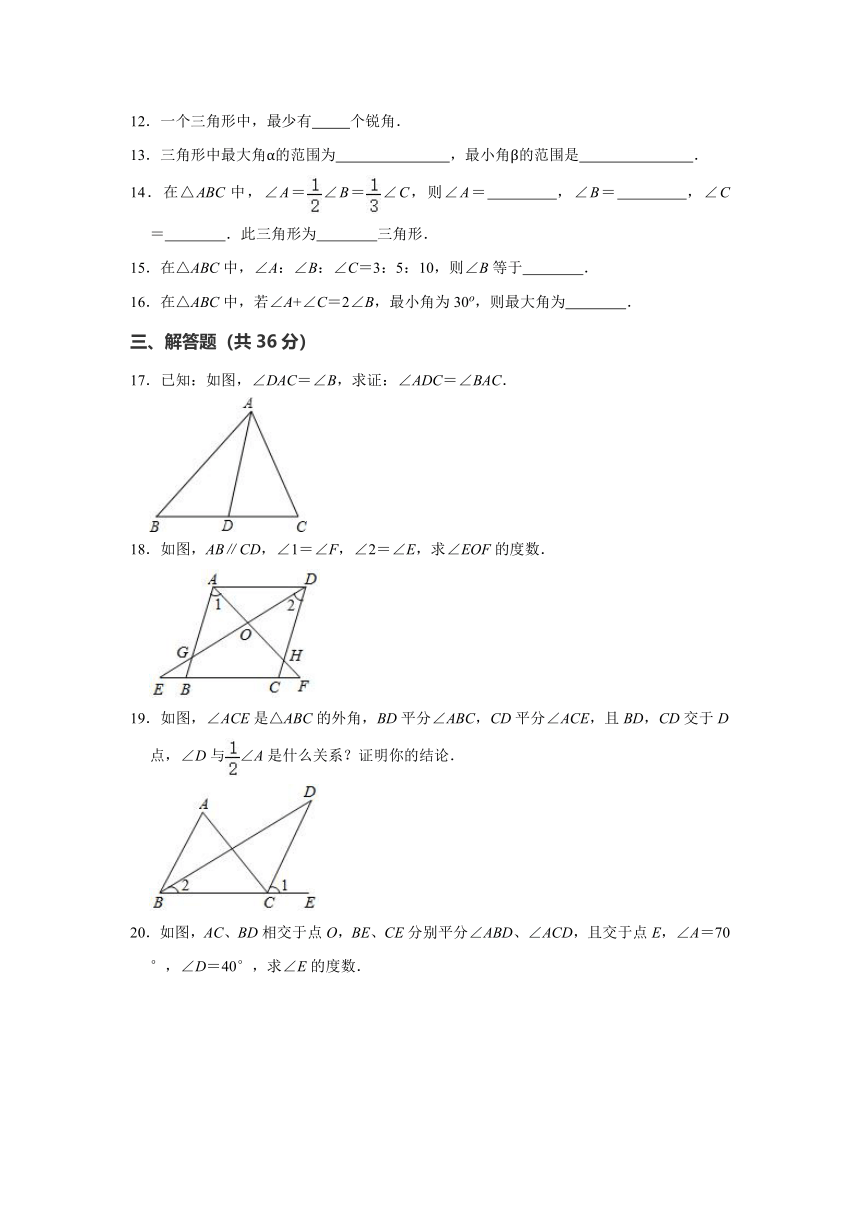
17.已知:如图,∠DAC=∠B,求证:∠ADC=∠BAC.
18.如图,AB∥CD,∠1=∠F,∠2=∠E,求∠EOF的度数.
19.如图,∠ACE是△ABC的外角,BD平分∠ABC,CD平分∠ACE,且BD,CD交于D点,∠D与∠A是什么关系?证明你的结论.
20.如图,AC、BD相交于点O,BE、CE分别平分∠ABD、∠ACD,且交于点E,∠A=70°,∠D=40°,求∠E的度数.
2020-2021学年七年级数学人教版(五四制)下册
第17章
三角形
单元检测试题
参考答案与试题解析
一.选择题(共10小题)
1.若一个三角形的三个内角互不相等,则它的最小角必小于( )
A.45°
B.60°
C.30°
D.90°
【分析】根据三角形的内角和定理进行分析.
【解答】解:根据三角形的内角和是180°,知
若三角形的三个内角相等,则每一个角是60°.
若三角形的三个内角互不相等,则它的最大角必,小于60°.
故选:B.
2.下列命题中,不正确的为( )
A.钝角三角形是斜三角形
B.在一个三角形中至多有一个内角不小于60o
C.三角形的没有公共顶点的两个外角的和大于平角
D.三角形的外角中,最小的一个是钝角,那它一定是锐角三角形
【分析】利用三角形的分类、三角形的内角、三角形的外角的性质等知识分别判断后即可确定正确的选项.
【解答】解:A、钝角三角形是斜三角形,正确,不符合题意;
B、在一个三角形中至少有一个内角不小于60°,错误,不符合题意;
C、三角形的没有公共顶点的两个外角的和大于平角,正确,符合题意;
D、三角形的外角中,最小的一个是钝角,那它一定是锐角三角形,正确,不符合题意,
故选:B.
3.以下命题正确的是( )
A.三角形三个外角的和是360o
B.三角形一个外角大于它的两个内角的和
C.三角形的外角都不大于90o
D.三角形中的内角没有大于120o的
【分析】利用三角形的性质分别判断后即可确定正确的选项.
【解答】解:A、三角形的三个外角的和是360°,正确,符合题意;
B、三角形的一个外角等于与它不相邻的两个内角的和,故原命题错误,不符合题意;
C、三角形的外角可以大于90°,故原命题错误,不符合题意;
D、三角形中的内角可以有大于120°的,故原命题错误,不符合题意,
故选:A.
4.下列说法正确的是( )
A.一个钝角三角形一定不是等腰三角形,也不是等边三角形
B.一个等腰三角形一定是锐角三角形,或直角三角形
C.一个直角三角形一定不是等腰三角形,也不是等边三角形
D.一个等边三角形一定不是钝角三角形,也不是直角三角形
【分析】根据钝角三角形、锐角三角形、直角三角形、等边三角形和等腰三角形之间的关系,分别进行判断,即可求出答案.
【解答】解:A、一个钝角三角形不一定不是等腰三角形,一定不是等边三角形,故本选项错误;
B、一个等腰三角形不一定是锐角三角形,或直角三角形,故本选项错误;
C、一个直角三角形不一定不是等腰三角形,一定不是等边三角形,故本选项错误;
D、一个等边三角形一定不是钝角三角形,也不是直角三角形,故本选项正确;
故选:D.
5.在三角形的三个外角(一个顶点只取一个外角)中,钝角的个数至少是( )
A.3
B.2
C.1
D.0
【分析】三角形的内角和是180度,在这三个角中最多有一个钝角,最少有2个锐角,因而外角中最多有一个锐角,至少有两个钝角.
【解答】解:因为三角形的每一个外角都与相邻的内角互补.
因为当相邻的内角是钝角时,这个外角才是锐角.
又因为三角形中最少有2个锐角,所以三角形的三个外角中至少有两个钝角.
故选:B.
6.如图,△ABC中,AD是BC边上中线,AE是BD边的中线,AF是DC边的中线,且AB<AC,则下列结论中错误的是( )
A.∠1>∠2>∠3>∠C
B.BE=ED=DF=FC
C.∠1>∠4+∠5+∠C
D.AE=AF
【分析】根据三角形的外角性质、三角形的中线的概念判断即可.
【解答】解:A、由三角形的外角性质可知,∠1>∠2,∠2>∠3,∠3>∠C,
∴∠1>∠2>∠3>∠C,本选项结论正确,不符合题意;
B、∵AD是BC边上中线,
∴BD=DC,
∵AE是BD边的中线,AF是DC边的中线,
∴BE=ED=BD,DF=FC=DC,
∴BE=ED=DF=FC,本选项结论正确,不符合题意;
C、由三角形的外角性质可知,∠1>∠2+∠4,∠2>∠3,∠3=∠5+∠C,
∴∠1>∠4+∠5+∠C,本选项结论正确,不符合题意;
D、∵AD是BC边上中线,AB<AC,
∴AD与BC不垂直,
∵ED=DF,
∴AE≠AF,本选项结论错误,符合题意;
故选:D.
7.锐角三角形中任意两个锐角的和必大于( )
A.120°
B.110°
C.100°
D.90°
【分析】根据三角形的内角和是180度和锐角三角形的定义可知:锐角三角形中任意两个锐角的和必大于90°.
【解答】解:如果两个锐角和不大于90°,那么第三个角将大于等于90°,就不再是锐角三角形.故选D.
8.如图,在△ADE中,引线段EB与EC,下列各等式中,正确的是( )
A.∠A+∠1+∠7=∠D+∠3+∠6
B.∠1+∠5=∠2+∠7
C.∠6+∠A=∠2+∠7
D.∠A+∠5+∠7=∠2+∠8+∠6
【分析】根据三角形的内角和定理以及三角形外角的性质得出各角的关系,即可作出判断.
【解答】解:∵∠6=∠A+∠1,∠7=∠3+∠D,
∴∠A+∠1+∠7=∠6+∠7,∠D+∠3+∠6=∠7+∠6,
∴∠A+∠1+∠7=∠D+∠3+∠6,故A正确;
∵∠1+∠5=180°﹣∠A=180°﹣∠A﹣∠1,
∴∠1+∠5≠∠2+∠7,
∠6+∠A=∠2+∠7,故C错误;
无法证出∠A+∠5+∠7=∠2+∠8+∠6,故D错误.
故选:A.
9.若一个三角形三个外角的度数之比为2:3:4,则与之对应的三个内角的度数的比为( )
A.5:3:1
B.3:2:4
C.4:3:2
D.3:1:5
【分析】已知三角形三个外角的度数之比,可以设一份为k°,根据三角形的外角和等于360°列方程求三个内角的度数,确定三角形内角的度数,然后求出度数之比.
【解答】解:设一份为k°,则三个外角的度数分别为2k°,3k°,4k°,
根据三角形外角和定理,可知2k°+3k°+4k°=360°,得k°=40°,
三个外角分别为80°,120°和160°,
根据三角形外角与它相邻的内角互补,与之对应的三个内角的度数分别是100°,60°和20°,
即三个内角的度数的比为5:3:1.
故选:A.
10.如图所示,已知∠1=60°,∠A+∠B+∠C+∠D+∠E+∠F=( )
A.180°
B.360°
C.240°
D.200°
【分析】根据“三角形的外角等于与它不相邻的两个内角和”可知∠B+∠D+∠C+∠E=180°﹣60°=120°,根据三角形内角和可知∠A+∠F=120°,∴∠A+∠B+∠C+∠D+∠E+∠F=120°+120°=240°.
【解答】解:∵∠3=∠B+∠D,∠2=∠C+∠E,∠2+∠3=180°﹣60°=120°,
∴∠B+∠D+∠C+∠E=180°﹣60°=120°,
∵∠A+∠F=120°,
∴∠A+∠B+∠C+∠D+∠E+∠F=120°+120°=240°.
故选:C.
二.填空题
11.在△ABC中,∠A是∠B的2倍,∠C比∠A+∠B还大12°,则这个三角形是 钝角 三角形.
【分析】设∠B为x,则∠A=2x,∠C=3x+12,根据三角形的内角和定理可列出方程,从而解出即可得出答案.
【解答】解:设∠B为x,则∠A=2x,∠C=3x+12,
由题意得:x+2x+3x+12=180°,
解得:x=28°,2x=56°,3x+12=96°,
即三角形为钝角三角形.
故答案为:钝角.
12.一个三角形中,最少有 2 个锐角.
【分析】根据三角形的内角和等于180°,三个角中最多有一个直角或钝角,所以最少有两个锐角.
【解答】解:∵三角形的内角和等于180°,
∴三角形最多有一个直角或钝角,剩下的两个为锐角.
∴一个三角形中,最少有2个锐角.
故答案为:2.
13.三角形中最大角α的范围为 60°≤α<180° ,最小角β的范围是 0°<β≤60° .
【分析】利用三角形内角和定理,用反证法来说明最大最小角的范围.
【解答】解:根据三角形内角和定理知,内角和为180°,则最大角不<60°;若最大角<60°,则三个内角的和就<了180°,这与内定理矛盾;
同样,最小应不>60°;若最小角>了60°,则三个内角的和就>了180°,这与内角和定理也矛盾.
故:三角形中最大角α的范围为60°≤α<180°,最小角β的范围是0°<β≤60°.
14.在△ABC中,∠A=∠B=∠C,则∠A= 30° ,∠B= 60° ,∠C= 90° .此三角形为 直角 三角形.
【分析】由题意可得∠B=2∠A,∠C=3∠A,根据三角形的内角和定理求出∠A,即可得∠B,∠C的度数,即可求解.
【解答】解:∵,∠A=∠B=∠C,
∴∠B=2∠A,∠C=3∠A,
∵∠A+∠B+∠C=180°,
∴6∠A=180°,
∴∠A=30°,
∴∠B=2∠A=60°,∠C=3∠A=90°,
∴此三角形为直角三角形.
故答案为:30°,60°,90°,直角.
15.在△ABC中,∠A:∠B:∠C=3:5:10,则∠B等于 50° .
【分析】设∠A=3k,∠B=5k,∠C=10k,由三角形内角和为180度可求出k,从而求出∠B.
【解答】解:由题意可设∠A=3k,∠B=5k,∠C=10k,
则3k+5k+10k=180°,
∴k=10°,
∴∠B=50°.
16.在△ABC中,若∠A+∠C=2∠B,最小角为30o,则最大角为 90° .
【分析】首先求出∠B=60°,不妨设∠A=30°,则∠C=180°﹣30°﹣60°=90°,即可即可解决问题.
【解答】解:∵∠A+∠C=2∠B,
又∵∠A+∠B+∠C=180°,
∴3∠B=180°,
∴∠B=60°,
设∠A=30°,则∠C=180°﹣30°﹣60°=90°,
∴△ABC中,最大的角为90°.
故答案为:90°.
三.解答题(共4小题)
17.已知:如图,∠DAC=∠B,求证:∠ADC=∠BAC.
【分析】利用三角形内角和定理进而求出即可.
【解答】证明:∵∠DAC=∠B,∠C=∠C,
∴∠ADC=180°﹣∠C﹣∠DAC,∠B=180°﹣∠C﹣∠BAC,
18.如图,AB∥CD,∠1=∠F,∠2=∠E,求∠EOF的度数.
【分析】根据平行线的性质进行解答即可.
【解答】解:∵AB∥CD,
∴∠1=∠CHF,∠2=BGE,∠ABC+∠DCB=180°,
又∵∠1=∠F,∠2=∠E,
∴∠1=∠CHF=∠F,∠2=∠BGE=∠E,
又∵∠ABC=∠BGE+∠E,∠DCB=∠CHF+∠F,
∴∠ABC+∠DCB=180°=2∠E+2∠F,
∴∠E+∠F=90°,
∴∠EOF=180°﹣(∠E+∠F)=180°﹣90°=90°,
答:∠EOF的度数为90°.
19.如图,∠ACE是△ABC的外角,BD平分∠ABC,CD平分∠ACE,且BD,CD交于D点,∠D与∠A是什么关系?证明你的结论.
【分析】根据角平分线定义得出∠ABC=2∠1,∠ACE=2∠2,根据三角形外角性质得出2∠D+∠ABC=∠A+∠ABC,求出∠A=2∠D,即可求出答案.
【解答】解:,
证明:∵BD平分∠ABC,CD平分∠ACE,
∴∠ABC=2∠2,∠ACE=2∠1,
∵∠ACE=2∠1=∠A+∠ABC,∠1=∠D+∠2,
∴2∠2=2∠D+2∠1,
∴∠ACE=2∠D+∠ABC,
∴2∠D+∠ABC=∠A+∠ABC,
∴∠A=2∠D,
∴∠D=∠A.
20.如图,AC、BD相交于点O,BE、CE分别平分∠ABD、∠ACD,且交于点E,∠A=70°,∠D=40°,求∠E的度数.
【分析】根据角平分线的性质及内角与外角的关系解答即可.
【解答】解:∵BE、CE分别平分∠ABD、∠ACD,
∴∠1=∠2,∠3=∠4,
∵∠CME=∠AMB,
∴∠A+∠1=∠E+∠3①,
∵∠ENB=∠DNC,
∴∠E+∠2=∠D+∠4②,
①﹣②得,∠A﹣∠E=∠E﹣∠D,
则∠E=(∠A+∠D)=55°.
答:∠E的度数是55°.
第17章
三角形
单元检测试题
一、选择题(每小题4分,共40分)
1.若一个三角形的三个内角互不相等,则它的最小角必小于( )
A.45°
B.60°
C.30°
D.90°
2.下列命题中,不正确的为( )
A.钝角三角形是斜三角形
B.在一个三角形中至多有一个内角不小于60o
C.三角形的没有公共顶点的两个外角的和大于平角
D.三角形的外角中,最小的一个是钝角,那它一定是锐角三角形
3.以下命题正确的是( )
A.三角形三个外角的和是360o
B.三角形一个外角大于它的两个内角的和
C.三角形的外角都不大于90o
D.三角形中的内角没有大于120o的
4.下列说法正确的是( )
A.一个钝角三角形一定不是等腰三角形,也不是等边三角形
B.一个等腰三角形一定是锐角三角形,或直角三角形
C.一个直角三角形一定不是等腰三角形,也不是等边三角形
D.一个等边三角形一定不是钝角三角形,也不是直角三角形
5.在三角形的三个外角(一个顶点只取一个外角)中,钝角的个数至少是( )
A.3
B.2
C.1
D.0
6.如图,△ABC中,AD是BC边上中线,AE是BD边的中线,AF是DC边的中线,且AB<AC,则下列结论中错误的是( )
A.∠1>∠2>∠3>∠C
B.BE=ED=DF=FC
C.∠1>∠4+∠5+∠C
D.AE=AF
7.锐角三角形中任意两个锐角的和必大于( )
A.120°
B.110°
C.100°
D.90°
8.如图,在△ADE中,引线段EB与EC,下列各等式中,正确的是( )
A.∠A+∠1+∠7=∠D+∠3+∠6
B.∠1+∠5=∠2+∠7
C.∠6+∠A=∠2+∠7
D.∠A+∠5+∠7=∠2+∠8+∠6
9.若一个三角形三个外角的度数之比为2:3:4,则与之对应的三个内角的度数的比为( )
A.5:3:1
B.3:2:4
C.4:3:2
D.3:1:5
10.如图所示,已知∠1=60°,∠A+∠B+∠C+∠D+∠E+∠F=( )
A.180°
B.360°
C.240°
D.200°
二、填空题(每小题4分,共24分)
11.在△ABC中,∠A是∠B的2倍,∠C比∠A+∠B还大12°,则这个三角形是
三角形.
12.一个三角形中,最少有
个锐角.
13.三角形中最大角α的范围为
,最小角β的范围是
.
14.在△ABC中,∠A=∠B=∠C,则∠A=
,∠B=
,∠C=
.此三角形为
三角形.
15.在△ABC中,∠A:∠B:∠C=3:5:10,则∠B等于
.
16.在△ABC中,若∠A+∠C=2∠B,最小角为30o,则最大角为
.
三、解答题(共36分)
17.已知:如图,∠DAC=∠B,求证:∠ADC=∠BAC.
18.如图,AB∥CD,∠1=∠F,∠2=∠E,求∠EOF的度数.
19.如图,∠ACE是△ABC的外角,BD平分∠ABC,CD平分∠ACE,且BD,CD交于D点,∠D与∠A是什么关系?证明你的结论.
20.如图,AC、BD相交于点O,BE、CE分别平分∠ABD、∠ACD,且交于点E,∠A=70°,∠D=40°,求∠E的度数.
2020-2021学年七年级数学人教版(五四制)下册
第17章
三角形
单元检测试题
参考答案与试题解析
一.选择题(共10小题)
1.若一个三角形的三个内角互不相等,则它的最小角必小于( )
A.45°
B.60°
C.30°
D.90°
【分析】根据三角形的内角和定理进行分析.
【解答】解:根据三角形的内角和是180°,知
若三角形的三个内角相等,则每一个角是60°.
若三角形的三个内角互不相等,则它的最大角必,小于60°.
故选:B.
2.下列命题中,不正确的为( )
A.钝角三角形是斜三角形
B.在一个三角形中至多有一个内角不小于60o
C.三角形的没有公共顶点的两个外角的和大于平角
D.三角形的外角中,最小的一个是钝角,那它一定是锐角三角形
【分析】利用三角形的分类、三角形的内角、三角形的外角的性质等知识分别判断后即可确定正确的选项.
【解答】解:A、钝角三角形是斜三角形,正确,不符合题意;
B、在一个三角形中至少有一个内角不小于60°,错误,不符合题意;
C、三角形的没有公共顶点的两个外角的和大于平角,正确,符合题意;
D、三角形的外角中,最小的一个是钝角,那它一定是锐角三角形,正确,不符合题意,
故选:B.
3.以下命题正确的是( )
A.三角形三个外角的和是360o
B.三角形一个外角大于它的两个内角的和
C.三角形的外角都不大于90o
D.三角形中的内角没有大于120o的
【分析】利用三角形的性质分别判断后即可确定正确的选项.
【解答】解:A、三角形的三个外角的和是360°,正确,符合题意;
B、三角形的一个外角等于与它不相邻的两个内角的和,故原命题错误,不符合题意;
C、三角形的外角可以大于90°,故原命题错误,不符合题意;
D、三角形中的内角可以有大于120°的,故原命题错误,不符合题意,
故选:A.
4.下列说法正确的是( )
A.一个钝角三角形一定不是等腰三角形,也不是等边三角形
B.一个等腰三角形一定是锐角三角形,或直角三角形
C.一个直角三角形一定不是等腰三角形,也不是等边三角形
D.一个等边三角形一定不是钝角三角形,也不是直角三角形
【分析】根据钝角三角形、锐角三角形、直角三角形、等边三角形和等腰三角形之间的关系,分别进行判断,即可求出答案.
【解答】解:A、一个钝角三角形不一定不是等腰三角形,一定不是等边三角形,故本选项错误;
B、一个等腰三角形不一定是锐角三角形,或直角三角形,故本选项错误;
C、一个直角三角形不一定不是等腰三角形,一定不是等边三角形,故本选项错误;
D、一个等边三角形一定不是钝角三角形,也不是直角三角形,故本选项正确;
故选:D.
5.在三角形的三个外角(一个顶点只取一个外角)中,钝角的个数至少是( )
A.3
B.2
C.1
D.0
【分析】三角形的内角和是180度,在这三个角中最多有一个钝角,最少有2个锐角,因而外角中最多有一个锐角,至少有两个钝角.
【解答】解:因为三角形的每一个外角都与相邻的内角互补.
因为当相邻的内角是钝角时,这个外角才是锐角.
又因为三角形中最少有2个锐角,所以三角形的三个外角中至少有两个钝角.
故选:B.
6.如图,△ABC中,AD是BC边上中线,AE是BD边的中线,AF是DC边的中线,且AB<AC,则下列结论中错误的是( )
A.∠1>∠2>∠3>∠C
B.BE=ED=DF=FC
C.∠1>∠4+∠5+∠C
D.AE=AF
【分析】根据三角形的外角性质、三角形的中线的概念判断即可.
【解答】解:A、由三角形的外角性质可知,∠1>∠2,∠2>∠3,∠3>∠C,
∴∠1>∠2>∠3>∠C,本选项结论正确,不符合题意;
B、∵AD是BC边上中线,
∴BD=DC,
∵AE是BD边的中线,AF是DC边的中线,
∴BE=ED=BD,DF=FC=DC,
∴BE=ED=DF=FC,本选项结论正确,不符合题意;
C、由三角形的外角性质可知,∠1>∠2+∠4,∠2>∠3,∠3=∠5+∠C,
∴∠1>∠4+∠5+∠C,本选项结论正确,不符合题意;
D、∵AD是BC边上中线,AB<AC,
∴AD与BC不垂直,
∵ED=DF,
∴AE≠AF,本选项结论错误,符合题意;
故选:D.
7.锐角三角形中任意两个锐角的和必大于( )
A.120°
B.110°
C.100°
D.90°
【分析】根据三角形的内角和是180度和锐角三角形的定义可知:锐角三角形中任意两个锐角的和必大于90°.
【解答】解:如果两个锐角和不大于90°,那么第三个角将大于等于90°,就不再是锐角三角形.故选D.
8.如图,在△ADE中,引线段EB与EC,下列各等式中,正确的是( )
A.∠A+∠1+∠7=∠D+∠3+∠6
B.∠1+∠5=∠2+∠7
C.∠6+∠A=∠2+∠7
D.∠A+∠5+∠7=∠2+∠8+∠6
【分析】根据三角形的内角和定理以及三角形外角的性质得出各角的关系,即可作出判断.
【解答】解:∵∠6=∠A+∠1,∠7=∠3+∠D,
∴∠A+∠1+∠7=∠6+∠7,∠D+∠3+∠6=∠7+∠6,
∴∠A+∠1+∠7=∠D+∠3+∠6,故A正确;
∵∠1+∠5=180°﹣∠A=180°﹣∠A﹣∠1,
∴∠1+∠5≠∠2+∠7,
∠6+∠A=∠2+∠7,故C错误;
无法证出∠A+∠5+∠7=∠2+∠8+∠6,故D错误.
故选:A.
9.若一个三角形三个外角的度数之比为2:3:4,则与之对应的三个内角的度数的比为( )
A.5:3:1
B.3:2:4
C.4:3:2
D.3:1:5
【分析】已知三角形三个外角的度数之比,可以设一份为k°,根据三角形的外角和等于360°列方程求三个内角的度数,确定三角形内角的度数,然后求出度数之比.
【解答】解:设一份为k°,则三个外角的度数分别为2k°,3k°,4k°,
根据三角形外角和定理,可知2k°+3k°+4k°=360°,得k°=40°,
三个外角分别为80°,120°和160°,
根据三角形外角与它相邻的内角互补,与之对应的三个内角的度数分别是100°,60°和20°,
即三个内角的度数的比为5:3:1.
故选:A.
10.如图所示,已知∠1=60°,∠A+∠B+∠C+∠D+∠E+∠F=( )
A.180°
B.360°
C.240°
D.200°
【分析】根据“三角形的外角等于与它不相邻的两个内角和”可知∠B+∠D+∠C+∠E=180°﹣60°=120°,根据三角形内角和可知∠A+∠F=120°,∴∠A+∠B+∠C+∠D+∠E+∠F=120°+120°=240°.
【解答】解:∵∠3=∠B+∠D,∠2=∠C+∠E,∠2+∠3=180°﹣60°=120°,
∴∠B+∠D+∠C+∠E=180°﹣60°=120°,
∵∠A+∠F=120°,
∴∠A+∠B+∠C+∠D+∠E+∠F=120°+120°=240°.
故选:C.
二.填空题
11.在△ABC中,∠A是∠B的2倍,∠C比∠A+∠B还大12°,则这个三角形是 钝角 三角形.
【分析】设∠B为x,则∠A=2x,∠C=3x+12,根据三角形的内角和定理可列出方程,从而解出即可得出答案.
【解答】解:设∠B为x,则∠A=2x,∠C=3x+12,
由题意得:x+2x+3x+12=180°,
解得:x=28°,2x=56°,3x+12=96°,
即三角形为钝角三角形.
故答案为:钝角.
12.一个三角形中,最少有 2 个锐角.
【分析】根据三角形的内角和等于180°,三个角中最多有一个直角或钝角,所以最少有两个锐角.
【解答】解:∵三角形的内角和等于180°,
∴三角形最多有一个直角或钝角,剩下的两个为锐角.
∴一个三角形中,最少有2个锐角.
故答案为:2.
13.三角形中最大角α的范围为 60°≤α<180° ,最小角β的范围是 0°<β≤60° .
【分析】利用三角形内角和定理,用反证法来说明最大最小角的范围.
【解答】解:根据三角形内角和定理知,内角和为180°,则最大角不<60°;若最大角<60°,则三个内角的和就<了180°,这与内定理矛盾;
同样,最小应不>60°;若最小角>了60°,则三个内角的和就>了180°,这与内角和定理也矛盾.
故:三角形中最大角α的范围为60°≤α<180°,最小角β的范围是0°<β≤60°.
14.在△ABC中,∠A=∠B=∠C,则∠A= 30° ,∠B= 60° ,∠C= 90° .此三角形为 直角 三角形.
【分析】由题意可得∠B=2∠A,∠C=3∠A,根据三角形的内角和定理求出∠A,即可得∠B,∠C的度数,即可求解.
【解答】解:∵,∠A=∠B=∠C,
∴∠B=2∠A,∠C=3∠A,
∵∠A+∠B+∠C=180°,
∴6∠A=180°,
∴∠A=30°,
∴∠B=2∠A=60°,∠C=3∠A=90°,
∴此三角形为直角三角形.
故答案为:30°,60°,90°,直角.
15.在△ABC中,∠A:∠B:∠C=3:5:10,则∠B等于 50° .
【分析】设∠A=3k,∠B=5k,∠C=10k,由三角形内角和为180度可求出k,从而求出∠B.
【解答】解:由题意可设∠A=3k,∠B=5k,∠C=10k,
则3k+5k+10k=180°,
∴k=10°,
∴∠B=50°.
16.在△ABC中,若∠A+∠C=2∠B,最小角为30o,则最大角为 90° .
【分析】首先求出∠B=60°,不妨设∠A=30°,则∠C=180°﹣30°﹣60°=90°,即可即可解决问题.
【解答】解:∵∠A+∠C=2∠B,
又∵∠A+∠B+∠C=180°,
∴3∠B=180°,
∴∠B=60°,
设∠A=30°,则∠C=180°﹣30°﹣60°=90°,
∴△ABC中,最大的角为90°.
故答案为:90°.
三.解答题(共4小题)
17.已知:如图,∠DAC=∠B,求证:∠ADC=∠BAC.
【分析】利用三角形内角和定理进而求出即可.
【解答】证明:∵∠DAC=∠B,∠C=∠C,
∴∠ADC=180°﹣∠C﹣∠DAC,∠B=180°﹣∠C﹣∠BAC,
18.如图,AB∥CD,∠1=∠F,∠2=∠E,求∠EOF的度数.
【分析】根据平行线的性质进行解答即可.
【解答】解:∵AB∥CD,
∴∠1=∠CHF,∠2=BGE,∠ABC+∠DCB=180°,
又∵∠1=∠F,∠2=∠E,
∴∠1=∠CHF=∠F,∠2=∠BGE=∠E,
又∵∠ABC=∠BGE+∠E,∠DCB=∠CHF+∠F,
∴∠ABC+∠DCB=180°=2∠E+2∠F,
∴∠E+∠F=90°,
∴∠EOF=180°﹣(∠E+∠F)=180°﹣90°=90°,
答:∠EOF的度数为90°.
19.如图,∠ACE是△ABC的外角,BD平分∠ABC,CD平分∠ACE,且BD,CD交于D点,∠D与∠A是什么关系?证明你的结论.
【分析】根据角平分线定义得出∠ABC=2∠1,∠ACE=2∠2,根据三角形外角性质得出2∠D+∠ABC=∠A+∠ABC,求出∠A=2∠D,即可求出答案.
【解答】解:,
证明:∵BD平分∠ABC,CD平分∠ACE,
∴∠ABC=2∠2,∠ACE=2∠1,
∵∠ACE=2∠1=∠A+∠ABC,∠1=∠D+∠2,
∴2∠2=2∠D+2∠1,
∴∠ACE=2∠D+∠ABC,
∴2∠D+∠ABC=∠A+∠ABC,
∴∠A=2∠D,
∴∠D=∠A.
20.如图,AC、BD相交于点O,BE、CE分别平分∠ABD、∠ACD,且交于点E,∠A=70°,∠D=40°,求∠E的度数.
【分析】根据角平分线的性质及内角与外角的关系解答即可.
【解答】解:∵BE、CE分别平分∠ABD、∠ACD,
∴∠1=∠2,∠3=∠4,
∵∠CME=∠AMB,
∴∠A+∠1=∠E+∠3①,
∵∠ENB=∠DNC,
∴∠E+∠2=∠D+∠4②,
①﹣②得,∠A﹣∠E=∠E﹣∠D,
则∠E=(∠A+∠D)=55°.
答:∠E的度数是55°.
