2020——2021学年沪科版九年级数学上册第21章 二次函数与反比例函数单元测试题(word版含解析)
文档属性
| 名称 | 2020——2021学年沪科版九年级数学上册第21章 二次函数与反比例函数单元测试题(word版含解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 133.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-01 00:00:00 | ||
图片预览



文档简介
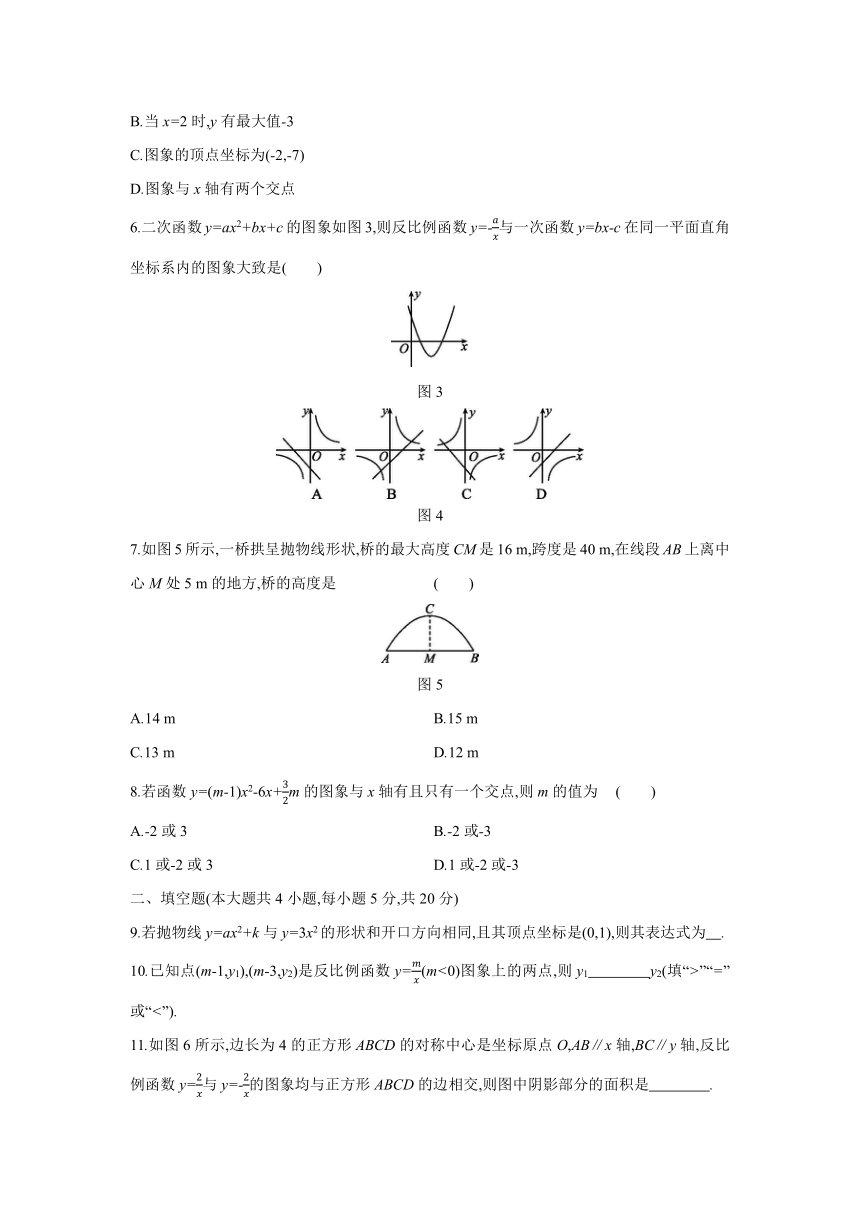
第21章 二次函数与反比例函数
一、选择题(本大题共8小题,每小题5分,共40分)
1.已知点(-1,4)在反比例函数y=的图象上,则下列各点在此函数图象上的是
( )
A.(4,-1)
B.(-,1)
C.(-4,-1)
D.(,2)
2.如图1,点P在反比例函数y=的图象上,PA⊥x轴于点A,若△PAO的面积为4,则k的值为
( )
图1
A.2
B.4
C.8
D.-4
3.将抛物线y=x2-2x+3平移得到抛物线y=x2,则这个平移过程正确的是
( )
A.先向左平移1个单位,再向下平移2个单位
B.先向左平移2个单位,再向下平移1个单位
C.先向右平移1个单位,再向上平移2个单位
D.先向右平移2个单位,再向上平移1个单位
4.若二次函数y=ax2+bx+c的部分图象如图2所示,则关于x的方程ax2+bx+c=0的解为( )
图2
A.x1=-2,x2=3
B.x1=-1,x2=3
C.x1=0,x2=3
D.x1=1,x2=3
5.对于二次函数y=-x2+x-4,下列说法正确的是
( )
A.当x>0时,y随x的增大而增大
B.当x=2时,y有最大值-3
C.图象的顶点坐标为(-2,-7)
D.图象与x轴有两个交点
6.二次函数y=ax2+bx+c的图象如图3,则反比例函数y=-与一次函数y=bx-c在同一平面直角坐标系内的图象大致是( )
图3
图4
7.如图5所示,一桥拱呈抛物线形状,桥的最大高度CM是16
m,跨度是40
m,在线段AB上离中心M处5
m的地方,桥的高度是
( )
图5
A.14
m
B.15
m
C.13
m
D.12
m
8.若函数y=(m-1)x2-6x+m的图象与x轴有且只有一个交点,则m的值为
( )
A.-2或3
B.-2或-3
C.1或-2或3
D.1或-2或-3
二、填空题(本大题共4小题,每小题5分,共20分)
9.若抛物线y=ax2+k与y=3x2的形状和开口方向相同,且其顶点坐标是(0,1),则其表达式为 .?
10.已知点(m-1,y1),(m-3,y2)是反比例函数y=(m<0)图象上的两点,则y1 y2(填“>”“=”或“<”).?
11.如图6所示,边长为4的正方形ABCD的对称中心是坐标原点O,AB∥x轴,BC∥y轴,反比例函数y=与y=-的图象均与正方形ABCD的边相交,则图中阴影部分的面积是 .?
图6
12.已知二次函数y=ax2+bx+c的图象如图7所示,给出以下结论:①b2>4ac;②abc>0;
③2a-b=0;④8a+c<0;⑤9a+3b+c<0.其中结论正确的是 (填写正确结论的序号).?
图7
三、解答题(本大题共3小题,共40分)
13.(12分)把抛物线C1:y=x2+2x+3先向右平移4个单位,再向下平移5个单位得到抛物线C2.
(1)直接写出抛物线C2的函数表达式;
(2)动点P(a,-6)能否在抛物线C2上?请说明理由;
(3)若点A(m,y1),B(n,y2)都在抛物线C2上,且m14.(14分)如图8,已知一次函数y=kx+b的图象与反比例函数y=的图象交于点A(3,a),点B(14-2a,2).
(1)求反比例函数的表达式;
(2)若一次函数图象与y轴交于点C,点D为点C关于原点O的对称点,求△ACD的面积.
图8
15.(14分)某水晶厂生产的水晶工艺品非常畅销,某网店专门销售这种工艺品.成本为30元/件,每天销售量y(件)与销售单价x(元/件)之间存在一次函数关系,当x=40时,y=300;当x=55时,y=150.
(1)求y与x之间的函数表达式(不必写出x的取值范围);
(2)如果规定每天工艺品的销售量不低于240件,当销售单价为多少时,每天获取的利润最大,最大利润是多少?
(3)该网店店主热心公益事业,决定从每天的销售利润中捐出150元给希望工程,为了保证捐款后每天剩余利润不低于3600元,试确定该工艺品销售单价的范围.
答案
1.A 2.C
3.[解析]
A 抛物线y=x2-2x+3=(x-1)2+2的顶点坐标为(1,2),将顶点向左平移1个单位,再向下平移2个单位,得(0,0),即平移后的抛物线为y=x2.
4.[解析]
B 根据抛物线的对称性,可知抛物线与x轴的另一个交点坐标为(-1,0),则方程的解为x1=-1,x2=3.
5.B
6.[解析]
C 由二次函数的图象知,a>0,c>0,对称轴x=->0,故有b<0.
当a>0时,反比例函数y=-的图象位于第二、四象限;当b<0,c>0时,一次函数y=bx-c的图象经过第二、三、四象限.故C正确.
7.[解析]
B 如图所示,建立平面直角坐标系,点A的坐标是(-20,0),点C的坐标是(0,16),设抛物线的表达式为y=ax2+k.把点A,C的坐标代入,得解得因此抛物线的表达式为y=-x2+16.把点D(5,0)的横坐标代入,得y=-×52+16=15(m).故选B.
8.C
9.[答案]
y=3x2+1
[解析]
因为两抛物线的形状和开口方向相同,所以a=3.将顶点坐标代入y=3x2+k可得k=1,故抛物线的表达式为y=3x2+1.
10.[答案]
>
[解析]
∵m<0,∴m-3y2.
11.[答案]
8
[解析]
反比例函数y=与y=-的图象所组成的图形关于x轴,y轴对称,因此阴影部分面积等于正方形ABCD面积的一半,即×4×4=8.
12.[答案]
①②⑤
[解析]
∵抛物线y=ax2+bx+c与x轴有两个交点,∴一元二次方程ax2+bx+c=0有两个不相等的实数根,∴b2-4ac>0,即b2>4ac,∴结论①是正确的.∵抛物线的开口方向向上,∴a>0.∵抛物线与y轴的交点在y轴的负半轴上,∴c<0.∵对称轴为直线x=-=1>0,
∴a与b异号,则b<0,∴abc>0,结论②是正确的.∵抛物线的对称轴为直线x=-=1,
∴b=-2a,∴2a+b=0,结论③是错误的.∵当x=-2时,y=4a-2b+c>0,b=-2a,∴4a-2b+c=4a-2(-2a)+c=8a+c>0,结论④是错误的.∵抛物线的对称轴为直线x=1,∴当x=-1与x=3时函数值相等.由函数图象可知当x=-1时的函数值为负数,∴当x=3时的函数值y=9a+3b+c<0,结论⑤是正确的.
综上所述,应填①②⑤.
13.解:(1)抛物线C2的函数表达式为y=x2-6x+6或y=(x-3)2-3.
(2)动点P不能在抛物线C2上.
理由如下:∵抛物线C2开口向上,且顶点坐标为(3,-3),
∴抛物线C2的最低点的纵坐标为-3.
∵yP=-6<-3,
∴动点P不能在抛物线C2上.
(3)y1>y2.
理由如下:由(1)知抛物线C2开口向上,对称轴是直线x=3,
∴在对称轴左侧,y随x的增大而减小.
∵点A(m,y1),B(n,y2)都在抛物线C2上,且m∴y1>y2.
14.解:(1)∵点A(3,a),点B(14-2a,2)在反比例函数y=的图象上,
∴3×a=(14-2a)×2,解得a=4.
∴m=3×4=12.
∴反比例函数的表达式是y=.
(2)∵a=4,
∴点A,B的坐标分别是(3,4),(6,2).
∵点A,B在一次函数y=kx+b的图象上,
∴解得
∴一次函数的表达式是y=-x+6.
当x=0时,y=6,
∴点C的坐标是(0,6).∴OC=6.
∵点D是点C关于原点O的对称点,
∴CD=2OC=12.
如图,过点A作AE⊥y轴于点E,
∴AE=3.
∴S△ACD=CD·AE=×12×3=18.
15.解:(1)设y与x之间的函数表达式为y=kx+b.
由题意,得解得
∴y与x之间的函数表达式为y=-10x+700.
(2)由题意,得-10x+700≥240,解得x≤46.
设每天获取的利润为w元,
则w=(x-30)·y
=(x-30)(-10x+700)
=-10x2+1000x-21000
=-10(x-50)2+4000.
∵-10<0,
∴当x<50时,w随x的增大而增大,
∴当x=46时,w最大值=-10×(46-50)2+4000=3840.
答:当销售单价为46元/件时,每天获取的利润最大,最大利润是3840元.
(3)由(2)得每天的利润w=-10x2+1000x-21000,
令w-150=3600,得-10x2+1000x-21000-150=3600,
∴-10(x-50)2=-250,
解得x1=55,x2=45.
∵a=-10<0,
∴当45≤x≤55时,捐款后每天剩余利润不低于3600元.
一、选择题(本大题共8小题,每小题5分,共40分)
1.已知点(-1,4)在反比例函数y=的图象上,则下列各点在此函数图象上的是
( )
A.(4,-1)
B.(-,1)
C.(-4,-1)
D.(,2)
2.如图1,点P在反比例函数y=的图象上,PA⊥x轴于点A,若△PAO的面积为4,则k的值为
( )
图1
A.2
B.4
C.8
D.-4
3.将抛物线y=x2-2x+3平移得到抛物线y=x2,则这个平移过程正确的是
( )
A.先向左平移1个单位,再向下平移2个单位
B.先向左平移2个单位,再向下平移1个单位
C.先向右平移1个单位,再向上平移2个单位
D.先向右平移2个单位,再向上平移1个单位
4.若二次函数y=ax2+bx+c的部分图象如图2所示,则关于x的方程ax2+bx+c=0的解为( )
图2
A.x1=-2,x2=3
B.x1=-1,x2=3
C.x1=0,x2=3
D.x1=1,x2=3
5.对于二次函数y=-x2+x-4,下列说法正确的是
( )
A.当x>0时,y随x的增大而增大
B.当x=2时,y有最大值-3
C.图象的顶点坐标为(-2,-7)
D.图象与x轴有两个交点
6.二次函数y=ax2+bx+c的图象如图3,则反比例函数y=-与一次函数y=bx-c在同一平面直角坐标系内的图象大致是( )
图3
图4
7.如图5所示,一桥拱呈抛物线形状,桥的最大高度CM是16
m,跨度是40
m,在线段AB上离中心M处5
m的地方,桥的高度是
( )
图5
A.14
m
B.15
m
C.13
m
D.12
m
8.若函数y=(m-1)x2-6x+m的图象与x轴有且只有一个交点,则m的值为
( )
A.-2或3
B.-2或-3
C.1或-2或3
D.1或-2或-3
二、填空题(本大题共4小题,每小题5分,共20分)
9.若抛物线y=ax2+k与y=3x2的形状和开口方向相同,且其顶点坐标是(0,1),则其表达式为 .?
10.已知点(m-1,y1),(m-3,y2)是反比例函数y=(m<0)图象上的两点,则y1 y2(填“>”“=”或“<”).?
11.如图6所示,边长为4的正方形ABCD的对称中心是坐标原点O,AB∥x轴,BC∥y轴,反比例函数y=与y=-的图象均与正方形ABCD的边相交,则图中阴影部分的面积是 .?
图6
12.已知二次函数y=ax2+bx+c的图象如图7所示,给出以下结论:①b2>4ac;②abc>0;
③2a-b=0;④8a+c<0;⑤9a+3b+c<0.其中结论正确的是 (填写正确结论的序号).?
图7
三、解答题(本大题共3小题,共40分)
13.(12分)把抛物线C1:y=x2+2x+3先向右平移4个单位,再向下平移5个单位得到抛物线C2.
(1)直接写出抛物线C2的函数表达式;
(2)动点P(a,-6)能否在抛物线C2上?请说明理由;
(3)若点A(m,y1),B(n,y2)都在抛物线C2上,且m
(1)求反比例函数的表达式;
(2)若一次函数图象与y轴交于点C,点D为点C关于原点O的对称点,求△ACD的面积.
图8
15.(14分)某水晶厂生产的水晶工艺品非常畅销,某网店专门销售这种工艺品.成本为30元/件,每天销售量y(件)与销售单价x(元/件)之间存在一次函数关系,当x=40时,y=300;当x=55时,y=150.
(1)求y与x之间的函数表达式(不必写出x的取值范围);
(2)如果规定每天工艺品的销售量不低于240件,当销售单价为多少时,每天获取的利润最大,最大利润是多少?
(3)该网店店主热心公益事业,决定从每天的销售利润中捐出150元给希望工程,为了保证捐款后每天剩余利润不低于3600元,试确定该工艺品销售单价的范围.
答案
1.A 2.C
3.[解析]
A 抛物线y=x2-2x+3=(x-1)2+2的顶点坐标为(1,2),将顶点向左平移1个单位,再向下平移2个单位,得(0,0),即平移后的抛物线为y=x2.
4.[解析]
B 根据抛物线的对称性,可知抛物线与x轴的另一个交点坐标为(-1,0),则方程的解为x1=-1,x2=3.
5.B
6.[解析]
C 由二次函数的图象知,a>0,c>0,对称轴x=->0,故有b<0.
当a>0时,反比例函数y=-的图象位于第二、四象限;当b<0,c>0时,一次函数y=bx-c的图象经过第二、三、四象限.故C正确.
7.[解析]
B 如图所示,建立平面直角坐标系,点A的坐标是(-20,0),点C的坐标是(0,16),设抛物线的表达式为y=ax2+k.把点A,C的坐标代入,得解得因此抛物线的表达式为y=-x2+16.把点D(5,0)的横坐标代入,得y=-×52+16=15(m).故选B.
8.C
9.[答案]
y=3x2+1
[解析]
因为两抛物线的形状和开口方向相同,所以a=3.将顶点坐标代入y=3x2+k可得k=1,故抛物线的表达式为y=3x2+1.
10.[答案]
>
[解析]
∵m<0,∴m-3
11.[答案]
8
[解析]
反比例函数y=与y=-的图象所组成的图形关于x轴,y轴对称,因此阴影部分面积等于正方形ABCD面积的一半,即×4×4=8.
12.[答案]
①②⑤
[解析]
∵抛物线y=ax2+bx+c与x轴有两个交点,∴一元二次方程ax2+bx+c=0有两个不相等的实数根,∴b2-4ac>0,即b2>4ac,∴结论①是正确的.∵抛物线的开口方向向上,∴a>0.∵抛物线与y轴的交点在y轴的负半轴上,∴c<0.∵对称轴为直线x=-=1>0,
∴a与b异号,则b<0,∴abc>0,结论②是正确的.∵抛物线的对称轴为直线x=-=1,
∴b=-2a,∴2a+b=0,结论③是错误的.∵当x=-2时,y=4a-2b+c>0,b=-2a,∴4a-2b+c=4a-2(-2a)+c=8a+c>0,结论④是错误的.∵抛物线的对称轴为直线x=1,∴当x=-1与x=3时函数值相等.由函数图象可知当x=-1时的函数值为负数,∴当x=3时的函数值y=9a+3b+c<0,结论⑤是正确的.
综上所述,应填①②⑤.
13.解:(1)抛物线C2的函数表达式为y=x2-6x+6或y=(x-3)2-3.
(2)动点P不能在抛物线C2上.
理由如下:∵抛物线C2开口向上,且顶点坐标为(3,-3),
∴抛物线C2的最低点的纵坐标为-3.
∵yP=-6<-3,
∴动点P不能在抛物线C2上.
(3)y1>y2.
理由如下:由(1)知抛物线C2开口向上,对称轴是直线x=3,
∴在对称轴左侧,y随x的增大而减小.
∵点A(m,y1),B(n,y2)都在抛物线C2上,且m
14.解:(1)∵点A(3,a),点B(14-2a,2)在反比例函数y=的图象上,
∴3×a=(14-2a)×2,解得a=4.
∴m=3×4=12.
∴反比例函数的表达式是y=.
(2)∵a=4,
∴点A,B的坐标分别是(3,4),(6,2).
∵点A,B在一次函数y=kx+b的图象上,
∴解得
∴一次函数的表达式是y=-x+6.
当x=0时,y=6,
∴点C的坐标是(0,6).∴OC=6.
∵点D是点C关于原点O的对称点,
∴CD=2OC=12.
如图,过点A作AE⊥y轴于点E,
∴AE=3.
∴S△ACD=CD·AE=×12×3=18.
15.解:(1)设y与x之间的函数表达式为y=kx+b.
由题意,得解得
∴y与x之间的函数表达式为y=-10x+700.
(2)由题意,得-10x+700≥240,解得x≤46.
设每天获取的利润为w元,
则w=(x-30)·y
=(x-30)(-10x+700)
=-10x2+1000x-21000
=-10(x-50)2+4000.
∵-10<0,
∴当x<50时,w随x的增大而增大,
∴当x=46时,w最大值=-10×(46-50)2+4000=3840.
答:当销售单价为46元/件时,每天获取的利润最大,最大利润是3840元.
(3)由(2)得每天的利润w=-10x2+1000x-21000,
令w-150=3600,得-10x2+1000x-21000-150=3600,
∴-10(x-50)2=-250,
解得x1=55,x2=45.
∵a=-10<0,
∴当45≤x≤55时,捐款后每天剩余利润不低于3600元.
