2020——2021学年沪科版九年级数学上册第22章 相似形单元测试题(word版有答案)
文档属性
| 名称 | 2020——2021学年沪科版九年级数学上册第22章 相似形单元测试题(word版有答案) |  | |
| 格式 | zip | ||
| 文件大小 | 739.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-01 07:45:41 | ||
图片预览



文档简介
第22章 相似形
一、选择题(本大题共10小题,每小题4分,满分40分)
1.下列图形一定是相似图形的是( )
A.两个菱形
B.两个矩形
C.两个等腰三角形
D.两个正五边形
2.如图1,在△ABC中,DE∥BC,DE与AB,AC分别交于点D,E.若AD=4,DB=2,则AE∶EC的值为( )
图1
A.
B.2
C.
D.
3.若如图2所示的两个四边形相似,则∠α的度数是( )
图2
A.60°
B.75°
C.87°
D.120°
4.如图3,线段AB两个端点的坐标分别为A(6,6),B(8,2),以原点O为位似中心,在第一象限内将线段AB缩小为原来的后得到线段CD,则端点C的坐标为( )
图3
A.(3,3)
B.(4,3)
C.(3,1)
D.(4,1)
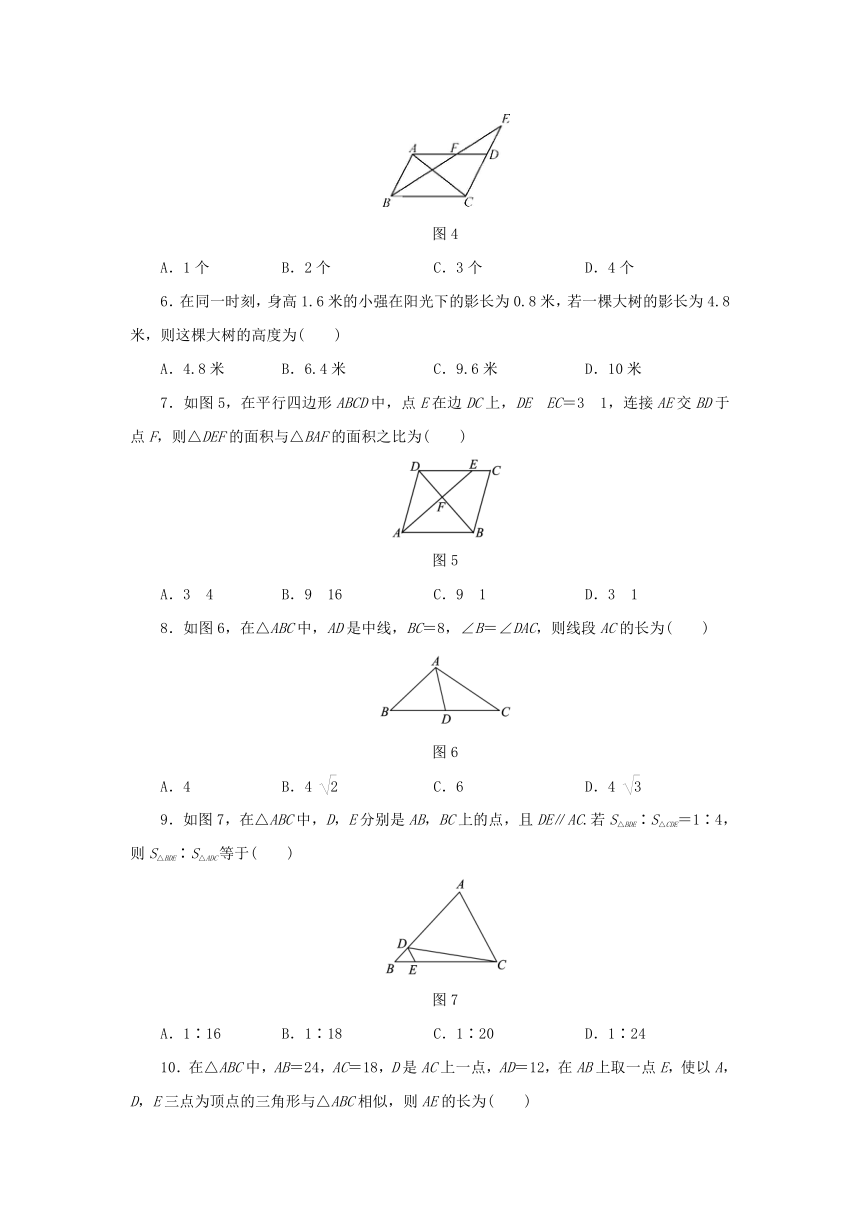
5.如图4所示,四边形ABCD是平行四边形,则图中与△DEF相似的三角形共有( )
图4
A.1个
B.2个
C.3个
D.4个
6.在同一时刻,身高1.6米的小强在阳光下的影长为0.8米,若一棵大树的影长为4.8米,则这棵大树的高度为( )
A.4.8米
B.6.4米
C.9.6米
D.10米
7.如图5,在平行四边形ABCD中,点E在边DC上,DE?EC=3?1,连接AE交BD于点F,则△DEF的面积与△BAF的面积之比为( )
图5
A.3?4
B.9?16
C.9?1
D.3?1
8.如图6,在△ABC中,AD是中线,BC=8,∠B=∠DAC,则线段AC的长为( )
图6
A.4
B.4
C.6
D.4
9.如图7,在△ABC中,D,E分别是AB,BC上的点,且DE∥AC.若S△BDE∶S△CDE=1∶4,则S△BDE∶S△ADC等于( )
图7
A.1∶16
B.1∶18
C.1∶20
D.1∶24
10.在△ABC中,AB=24,AC=18,D是AC上一点,AD=12,在AB上取一点E,使以A,D,E三点为顶点的三角形与△ABC相似,则AE的长为( )
A.16
B.14
C.16或14
D.16或9
二、填空题(本大题共4小题,每小题5分,满分20分)
11.若==≠0,则=________.
12.如图8,在△ABC中,D是AB边上的一点,连接CD,请添加一个适当的条件:____________________,使△ACD∽△ABC.(只填一个即可)
图8
13.如图9,已知△OAB与△OA′B′是相似比为1∶2的位似图形,点O为位似中心.若△OAB内一点P(x,y)与△OA′B′内一点P′是一对对应点,则点P′的坐标是__________.
图9
14.如图10,在Rt△ABC中,∠ACB=90°,D为AC上一点,将△ABC沿BD折叠,点C恰巧落在边AB上的点C′处,点E在AB上,连接DE,得△BED,若△BED与△ABC相似,则其相似比为________.
图10
三、(本大题共2小题,每小题8分,满分16分)
15.如图11,已知AD∥BE∥CF,它们依次交直线l1,l2于点A,B,C和点D,E,F.如果AB=6,BC=8,DF=21,求DE的长.
图11
16.如图12,在△ABC与△DEF中,∠C=54°,∠A=47°,∠F=54°,∠E=79°.求证:△ABC∽△DEF.
图12
四、(本大题共2小题,每小题8分,满分16分)
17.如图13,△ABC在方格纸中(方格纸中每个小正方形的边长均为1个单位).
(1)请在方格纸上建立平面直角坐标系,使A(2,3),C(6,2),并写出点B的坐标;
(2)在(1)的基础上,以原点O为位似中心,相似比为2,在第一象限内将△ABC放大,画出放大后的图形△A′B′C′(点A与点A′是对应点,点B与点B′是对应点,点C与点C′是对应点).
图13
18.如图14,D是△ABC的边AB上一点,BD=,AB=3,BC=2.
(1)△BCD与△BAC相似吗?请说明理由;
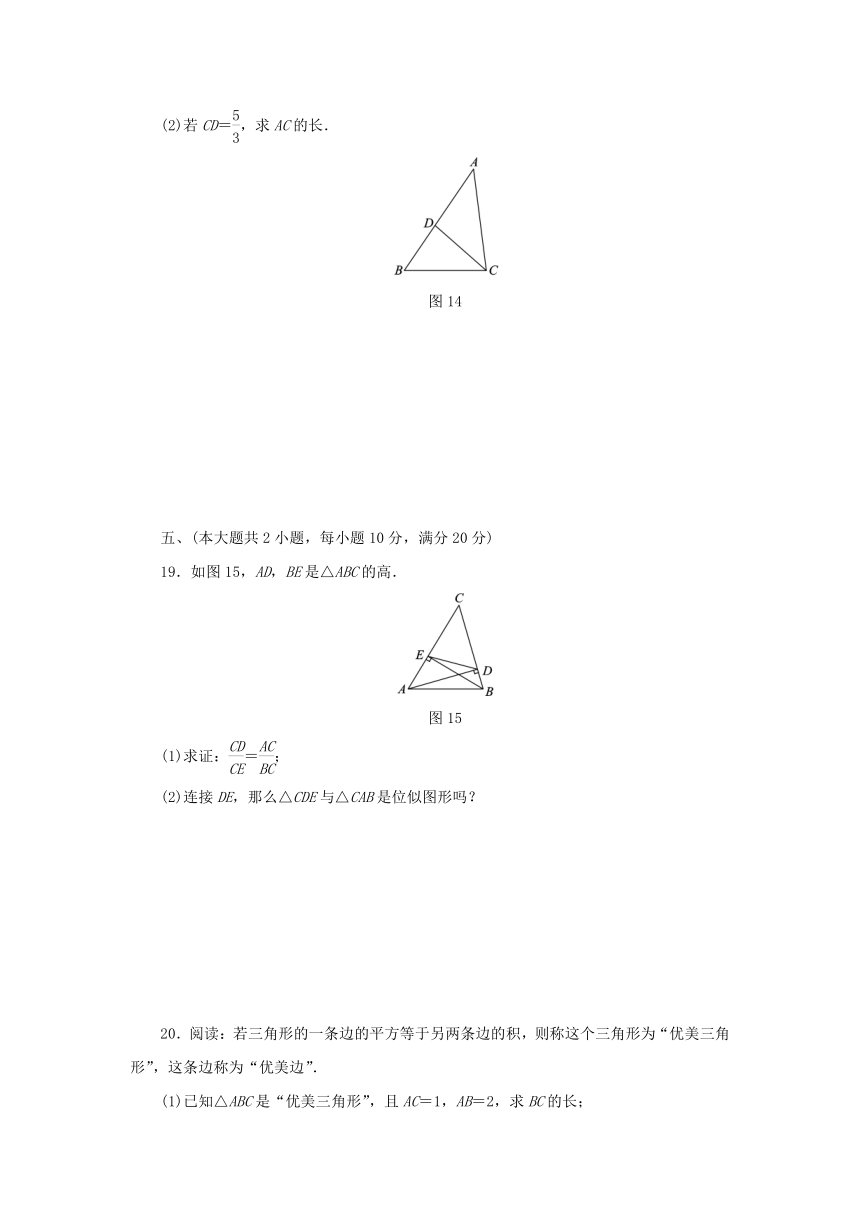
(2)若CD=,求AC的长.
图14
五、(本大题共2小题,每小题10分,满分20分)
19.如图15,AD,BE是△ABC的高.
图15
(1)求证:=;
(2)连接DE,那么△CDE与△CAB是位似图形吗?
20.阅读:若三角形的一条边的平方等于另两条边的积,则称这个三角形为“优美三角形”,这条边称为“优美边”.
(1)已知△ABC是“优美三角形”,且AC=1,AB=2,求BC的长;
(2)如图16,在四边形ABCD中,AB=AD,AD∥BC,∠ABC=∠ACD.求证:△ABC是“优美三角形”.
图16
六、(本题满分12分)
21.小明想利用太阳光测量楼高,他带着皮尺来到一栋楼下,发现对面墙上有这栋楼的影子,针对这种情况,他设计了一种测量方案,具体测量情况如下:
如图17(示意图),小明边移动边观察,发现站到点E处时,可以使自己落在墙上的影子与这栋楼落在墙上的影子重叠,且高度恰好相同.此时,测得小明落在墙上的影子高度CD=1.2
m,小明到墙的距离CE=0.8
m,楼到墙的距离CA=30
m(点A,E,C在同一直线上).已知小明的身高EF是1.7
m,请你帮小明求出楼高AB(结果精确到0.1
m).
图17
七、(本题满分12分)
22.如图18所示,正方形ABCD的边长为4
cm,P是边BC上不与点B,C重合的任意一点,连接AP,过点P作PQ⊥AP交DC于点Q.设BP的长为x
cm,CQ的长为y
cm.
(1)求点P在边BC上运动的过程中y的最大值;
(2)当y=时,求x的值.
图18
八、(本题满分14分)
23.如图19,在△ABC中,∠ABC=90°,AB=BC,D是AC边所在直线上的一个动点,DE⊥BD交BC边所在直线于点E.
(1)在图①中,AD=CD,直接写出的值;
(2)在图②中,AD=2CD,直接写出的值;
(3)在图③中,AD=CD,先写出的值,再说明理由.
图19
答案
1.D 2.B 3.C 4.A 5.B
6.C 7.B 8.B 9.C 10.D
11.
12.答案不唯一,如∠ADC=∠ACB或∠ACD=∠B或=
13.(-2x,-2y)
14.或
15.解:∵AD∥BE∥CF,∴=.
4分
∵AB=6,BC=8,DF=21,
∴=,
6分
∴DE=9.
8分
16.证明:在△ABC中,∠B=180°-∠A-∠C=79°.∵∠E=79°,∴∠B=∠E.
3分
∵∠C=54°,∠F=54°,∴∠C=∠F,
6分
∴△ABC∽△DEF.
8分
17.解:(1)平面直角坐标系如图所示,B(2,1).
4分
(2)△A'B'C'如图所示.
8分
18.解:(1)△BCD∽△BAC.理由如下:
∵BD=,AB=3,BC=2,
∴=,=,
∴=.
而∠DBC=∠CBA,
∴△BCD∽△BAC.
4分
(2)∵△BCD∽△BAC,
∴=,
即=,∴AC=.
8分
19.解:(1)证明:∵AD,BE是△ABC的高,
∴∠ADC=∠BEC=90°.
又∵∠C=∠C,∴△ADC∽△BEC,
∴=.
7分
(2)△CDE与△CAB不是位似图形.
10分
20.解:(1)由题意,易得AB,AC都不可能为“优美边”,否则三线段不能构成三角形.
由BC2=1×2,得BC=.
5分
(2)证明:∵AD∥BC,∴∠DAC=∠ACB.
又∵∠ABC=∠ACD,∴△ABC∽△DCA,
∴=,即AC2=BC·AD.
∵AB=AD,∴AC2=BC·AB,
∴△ABC是“优美三角形”.
10分
21.解:如图,过点D作DG⊥AB,与AB,EF分别交于点G,H,则EH=AG=CD=1.2
m,DH=CE=0.8
m,
DG=CA=30
m.
2分
∵EF∥AB,∴△DFH∽△DBG,
4分
∴=.
6分
由题意,知FH=EF-EH=1.7-1.2=0.5(m),
8分
∴=,解得BG=18.75(m),
10分
∴AB=BG+AG=18.75+1.2=19.95≈20.0(m).
答:楼高AB约为20.0
m.
12分
22.解:(1)∵PQ⊥AP,∴∠CPQ+∠APB=90°.
又∵∠BAP+∠APB=90°,
∴∠CPQ=∠BAP.
2分
又∵∠B=∠C=90°,
∴△ABP∽△PCQ,
4分
∴=.
∵AB=BC=4
cm,BP=x
cm,CQ=y
cm,
∴PC=(4-x)cm,
∴=,∴y=-x2+x,
即y=-(x-2)2+1(0∴当x=2时,y有最大值,最大值为1,即点P在边BC上运动的过程中,y的最大值为1.
6分
(2)x=2+或x=2-.
12分
23.解:(1)如图①,过点D作DF⊥BC于点F.
∵在△ABC中,∠ABC=90°,AB=BC,
∴∠ACB=45°,∴△DFC是等腰直角三角形,∴DF=CF.
∵∠DFC=∠ABC=90°,∠DCF=∠ACB=45°,
∴△DFC∽△ABC,∴=.
∵AD=CD,∴=.
设DF=CF=2k,则AB=BC=3k,∴BF=k.
易证△BDF∽△DEF,
∴===.
4分
(2)如图②,过点D作DF⊥BE于点F,同(1)可得△CDF是等腰直角三角形,∴CF=DF.
∵AD=2CD,∴AC=CD.
在△ABC与△DFC中,
∴△ABC≌△DFC,∴AB=DF,BC=FC,
∴AB=BC=FC=DF,∴BF=2DF.
易证△BDF∽△DEF,
∴==2.
8分
(3)=.
理由:如图③,过点D作DF⊥CE于点F.
∵在△ABC中,∠ABC=90°,AB=BC,
∴∠ACB=45°,
∴△DFC是等腰直角三角形,
∴DF=CF.
∵∠DFC=∠ABC=90°,∠DCF=∠ACB=45°,
∴△DFC∽△ABC,∴=.
∵AD=CD,∴==2.
设AB=m,则DF=2m,BC=m,CF=2m,
∴BF=m.
易证△BDF∽△DEF,
∴===.
14分
一、选择题(本大题共10小题,每小题4分,满分40分)
1.下列图形一定是相似图形的是( )
A.两个菱形
B.两个矩形
C.两个等腰三角形
D.两个正五边形
2.如图1,在△ABC中,DE∥BC,DE与AB,AC分别交于点D,E.若AD=4,DB=2,则AE∶EC的值为( )
图1
A.
B.2
C.
D.
3.若如图2所示的两个四边形相似,则∠α的度数是( )
图2
A.60°
B.75°
C.87°
D.120°
4.如图3,线段AB两个端点的坐标分别为A(6,6),B(8,2),以原点O为位似中心,在第一象限内将线段AB缩小为原来的后得到线段CD,则端点C的坐标为( )
图3
A.(3,3)
B.(4,3)
C.(3,1)
D.(4,1)
5.如图4所示,四边形ABCD是平行四边形,则图中与△DEF相似的三角形共有( )
图4
A.1个
B.2个
C.3个
D.4个
6.在同一时刻,身高1.6米的小强在阳光下的影长为0.8米,若一棵大树的影长为4.8米,则这棵大树的高度为( )
A.4.8米
B.6.4米
C.9.6米
D.10米
7.如图5,在平行四边形ABCD中,点E在边DC上,DE?EC=3?1,连接AE交BD于点F,则△DEF的面积与△BAF的面积之比为( )
图5
A.3?4
B.9?16
C.9?1
D.3?1
8.如图6,在△ABC中,AD是中线,BC=8,∠B=∠DAC,则线段AC的长为( )
图6
A.4
B.4
C.6
D.4
9.如图7,在△ABC中,D,E分别是AB,BC上的点,且DE∥AC.若S△BDE∶S△CDE=1∶4,则S△BDE∶S△ADC等于( )
图7
A.1∶16
B.1∶18
C.1∶20
D.1∶24
10.在△ABC中,AB=24,AC=18,D是AC上一点,AD=12,在AB上取一点E,使以A,D,E三点为顶点的三角形与△ABC相似,则AE的长为( )
A.16
B.14
C.16或14
D.16或9
二、填空题(本大题共4小题,每小题5分,满分20分)
11.若==≠0,则=________.
12.如图8,在△ABC中,D是AB边上的一点,连接CD,请添加一个适当的条件:____________________,使△ACD∽△ABC.(只填一个即可)
图8
13.如图9,已知△OAB与△OA′B′是相似比为1∶2的位似图形,点O为位似中心.若△OAB内一点P(x,y)与△OA′B′内一点P′是一对对应点,则点P′的坐标是__________.
图9
14.如图10,在Rt△ABC中,∠ACB=90°,D为AC上一点,将△ABC沿BD折叠,点C恰巧落在边AB上的点C′处,点E在AB上,连接DE,得△BED,若△BED与△ABC相似,则其相似比为________.
图10
三、(本大题共2小题,每小题8分,满分16分)
15.如图11,已知AD∥BE∥CF,它们依次交直线l1,l2于点A,B,C和点D,E,F.如果AB=6,BC=8,DF=21,求DE的长.
图11
16.如图12,在△ABC与△DEF中,∠C=54°,∠A=47°,∠F=54°,∠E=79°.求证:△ABC∽△DEF.
图12
四、(本大题共2小题,每小题8分,满分16分)
17.如图13,△ABC在方格纸中(方格纸中每个小正方形的边长均为1个单位).
(1)请在方格纸上建立平面直角坐标系,使A(2,3),C(6,2),并写出点B的坐标;
(2)在(1)的基础上,以原点O为位似中心,相似比为2,在第一象限内将△ABC放大,画出放大后的图形△A′B′C′(点A与点A′是对应点,点B与点B′是对应点,点C与点C′是对应点).
图13
18.如图14,D是△ABC的边AB上一点,BD=,AB=3,BC=2.
(1)△BCD与△BAC相似吗?请说明理由;
(2)若CD=,求AC的长.
图14
五、(本大题共2小题,每小题10分,满分20分)
19.如图15,AD,BE是△ABC的高.
图15
(1)求证:=;
(2)连接DE,那么△CDE与△CAB是位似图形吗?
20.阅读:若三角形的一条边的平方等于另两条边的积,则称这个三角形为“优美三角形”,这条边称为“优美边”.
(1)已知△ABC是“优美三角形”,且AC=1,AB=2,求BC的长;
(2)如图16,在四边形ABCD中,AB=AD,AD∥BC,∠ABC=∠ACD.求证:△ABC是“优美三角形”.
图16
六、(本题满分12分)
21.小明想利用太阳光测量楼高,他带着皮尺来到一栋楼下,发现对面墙上有这栋楼的影子,针对这种情况,他设计了一种测量方案,具体测量情况如下:
如图17(示意图),小明边移动边观察,发现站到点E处时,可以使自己落在墙上的影子与这栋楼落在墙上的影子重叠,且高度恰好相同.此时,测得小明落在墙上的影子高度CD=1.2
m,小明到墙的距离CE=0.8
m,楼到墙的距离CA=30
m(点A,E,C在同一直线上).已知小明的身高EF是1.7
m,请你帮小明求出楼高AB(结果精确到0.1
m).
图17
七、(本题满分12分)
22.如图18所示,正方形ABCD的边长为4
cm,P是边BC上不与点B,C重合的任意一点,连接AP,过点P作PQ⊥AP交DC于点Q.设BP的长为x
cm,CQ的长为y
cm.
(1)求点P在边BC上运动的过程中y的最大值;
(2)当y=时,求x的值.
图18
八、(本题满分14分)
23.如图19,在△ABC中,∠ABC=90°,AB=BC,D是AC边所在直线上的一个动点,DE⊥BD交BC边所在直线于点E.
(1)在图①中,AD=CD,直接写出的值;
(2)在图②中,AD=2CD,直接写出的值;
(3)在图③中,AD=CD,先写出的值,再说明理由.
图19
答案
1.D 2.B 3.C 4.A 5.B
6.C 7.B 8.B 9.C 10.D
11.
12.答案不唯一,如∠ADC=∠ACB或∠ACD=∠B或=
13.(-2x,-2y)
14.或
15.解:∵AD∥BE∥CF,∴=.
4分
∵AB=6,BC=8,DF=21,
∴=,
6分
∴DE=9.
8分
16.证明:在△ABC中,∠B=180°-∠A-∠C=79°.∵∠E=79°,∴∠B=∠E.
3分
∵∠C=54°,∠F=54°,∴∠C=∠F,
6分
∴△ABC∽△DEF.
8分
17.解:(1)平面直角坐标系如图所示,B(2,1).
4分
(2)△A'B'C'如图所示.
8分
18.解:(1)△BCD∽△BAC.理由如下:
∵BD=,AB=3,BC=2,
∴=,=,
∴=.
而∠DBC=∠CBA,
∴△BCD∽△BAC.
4分
(2)∵△BCD∽△BAC,
∴=,
即=,∴AC=.
8分
19.解:(1)证明:∵AD,BE是△ABC的高,
∴∠ADC=∠BEC=90°.
又∵∠C=∠C,∴△ADC∽△BEC,
∴=.
7分
(2)△CDE与△CAB不是位似图形.
10分
20.解:(1)由题意,易得AB,AC都不可能为“优美边”,否则三线段不能构成三角形.
由BC2=1×2,得BC=.
5分
(2)证明:∵AD∥BC,∴∠DAC=∠ACB.
又∵∠ABC=∠ACD,∴△ABC∽△DCA,
∴=,即AC2=BC·AD.
∵AB=AD,∴AC2=BC·AB,
∴△ABC是“优美三角形”.
10分
21.解:如图,过点D作DG⊥AB,与AB,EF分别交于点G,H,则EH=AG=CD=1.2
m,DH=CE=0.8
m,
DG=CA=30
m.
2分
∵EF∥AB,∴△DFH∽△DBG,
4分
∴=.
6分
由题意,知FH=EF-EH=1.7-1.2=0.5(m),
8分
∴=,解得BG=18.75(m),
10分
∴AB=BG+AG=18.75+1.2=19.95≈20.0(m).
答:楼高AB约为20.0
m.
12分
22.解:(1)∵PQ⊥AP,∴∠CPQ+∠APB=90°.
又∵∠BAP+∠APB=90°,
∴∠CPQ=∠BAP.
2分
又∵∠B=∠C=90°,
∴△ABP∽△PCQ,
4分
∴=.
∵AB=BC=4
cm,BP=x
cm,CQ=y
cm,
∴PC=(4-x)cm,
∴=,∴y=-x2+x,
即y=-(x-2)2+1(0
6分
(2)x=2+或x=2-.
12分
23.解:(1)如图①,过点D作DF⊥BC于点F.
∵在△ABC中,∠ABC=90°,AB=BC,
∴∠ACB=45°,∴△DFC是等腰直角三角形,∴DF=CF.
∵∠DFC=∠ABC=90°,∠DCF=∠ACB=45°,
∴△DFC∽△ABC,∴=.
∵AD=CD,∴=.
设DF=CF=2k,则AB=BC=3k,∴BF=k.
易证△BDF∽△DEF,
∴===.
4分
(2)如图②,过点D作DF⊥BE于点F,同(1)可得△CDF是等腰直角三角形,∴CF=DF.
∵AD=2CD,∴AC=CD.
在△ABC与△DFC中,
∴△ABC≌△DFC,∴AB=DF,BC=FC,
∴AB=BC=FC=DF,∴BF=2DF.
易证△BDF∽△DEF,
∴==2.
8分
(3)=.
理由:如图③,过点D作DF⊥CE于点F.
∵在△ABC中,∠ABC=90°,AB=BC,
∴∠ACB=45°,
∴△DFC是等腰直角三角形,
∴DF=CF.
∵∠DFC=∠ABC=90°,∠DCF=∠ACB=45°,
∴△DFC∽△ABC,∴=.
∵AD=CD,∴==2.
设AB=m,则DF=2m,BC=m,CF=2m,
∴BF=m.
易证△BDF∽△DEF,
∴===.
14分
