2020-2021学年安徽省亳州市七年级(下)期末数学试卷(word版含解析)
文档属性
| 名称 | 2020-2021学年安徽省亳州市七年级(下)期末数学试卷(word版含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 578.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-31 00:00:00 | ||
图片预览




文档简介
2020-2021学年安徽省亳州市七年级(下)期末数学试卷
一、选择题(共10小题,每小题4分,共40分).
1.下列实数中,属于无理数的是( )
A.﹣ B.3.14 C. D.
2.如图,已知AC⊥BC,CD⊥AB于点D,表示点A到直线CD的距离的是( )
A.线段CD的长度 B.线段AC的长度
C.线段AD的长度 D.线段BC的长度
3.下列计算正确的是( )
A.a2+a3=a5 B.a2?a3=a6 C.(2a)3=6a3 D.(a2)3=a6
4.若A(m2﹣3n)=m3﹣3mn,则代数式A的值为( )
A.m B.mn C.mn2 D.m2n
5.下列各式中,能运用完全平方公式分解因式的是( )
A.﹣x2﹣4 B.x2﹣4x+4 C.﹣x2+4x+4 D.4x2+4x+4
6.若x>y,下列不等式中一定成立的是( )
A.mx<my B.x2>y2 C.xc2>yc2 D.x﹣a>y﹣a
7.计算(x2+mx)(4x﹣8)的结果中不含x2项,则m的值是( )
A.﹣2 B.2 C.﹣1 D.1
8.如图,下列条件能判定AD∥BC的是( )
A.∠MAD=∠D B.∠D=∠DCN
C.∠B=∠DCN D.∠B+∠BCD=180°
9.在一个长、宽、高分别为8cm,4cm,2cm的长方体容器中装满水,将容器中的水全部倒入一个正方体容器中,恰好倒满(两容器的厚度忽略不计),则此正方体容器的棱长是( )
A.2cm B.4cm C.6cm D.8cm
10.若|x+y﹣5|+=0,则x2+y2的值为( )
A.19 B.31 C.27 D.23
二、填空题(本大题共4小题,每小题5分,满分20分)
11.如图,AC⊥BC,直线EF经过点C,若∠1=37°,则∠2的度数是 .
12.因式分解:3ax2﹣3ay2= .
13.如图,将周长为12cm的三角形ABC沿边BC向右平移5cm,得到三角形A′B′C′,则四边形AA′C′B的周长是 cm.
14.已知关于x的分式方程+=﹣2.
(1)如果该方程的解是x=2,那么m的值等于 ;
(2)如果该方程的解为正数,那么m的取值范围是 .
三、(本大题共2小题,每小题8分,满分16分)
15.计算:(π﹣2021)0+﹣()﹣2.
16.解不等式:﹣x≥﹣1.
四、(本大题共2小题,每小题8分,满分16分)
17.已知x+7的平方根是±3,2x+y﹣13的立方根是1,求的值.
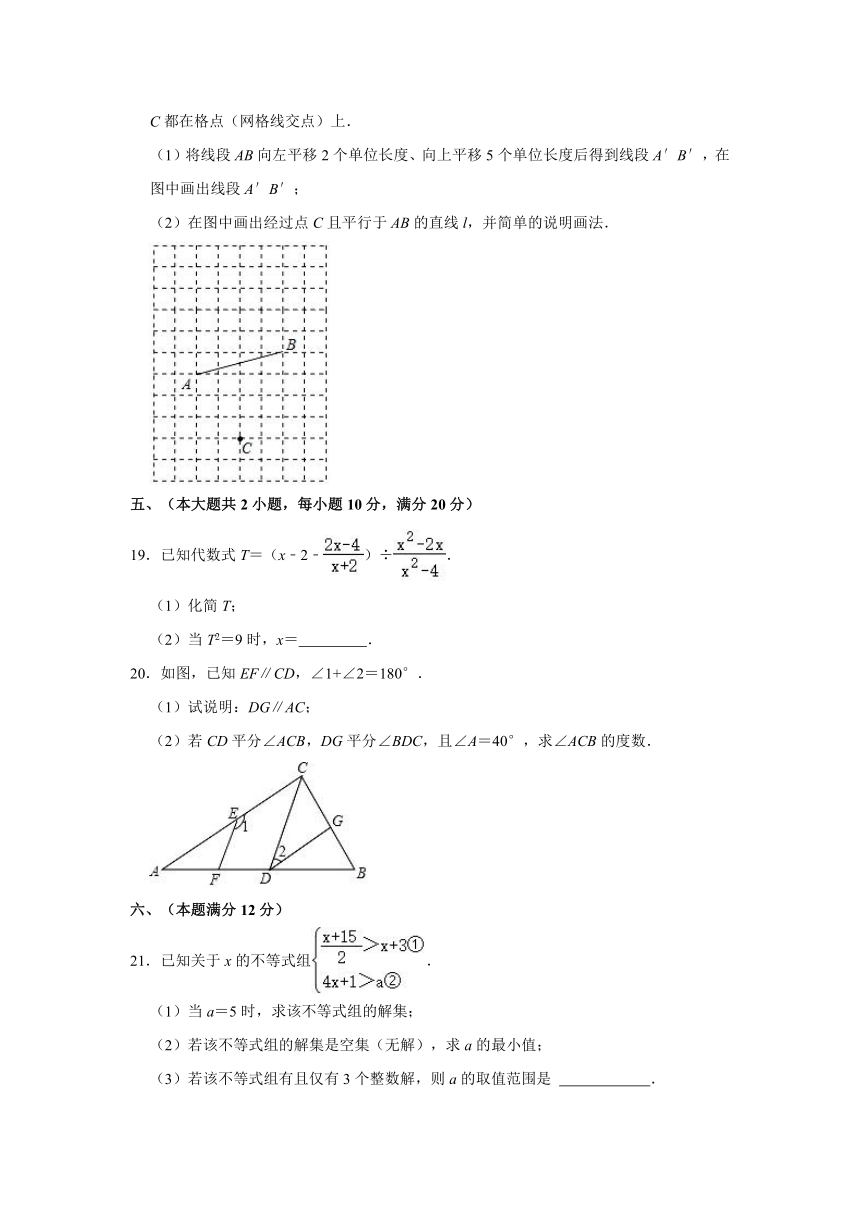
18.如图,在正方形网格中,每个小正方形的边长都为1个单位长度,线段AB的端点及点C都在格点(网格线交点)上.
(1)将线段AB向左平移2个单位长度、向上平移5个单位长度后得到线段A′B′,在图中画出线段A′B′;
(2)在图中画出经过点C且平行于AB的直线l,并简单的说明画法.
五、(本大题共2小题,每小题10分,满分20分)
19.已知代数式T=(x﹣2﹣)÷.
(1)化简T;
(2)当T2=9时,x= .
20.如图,已知EF∥CD,∠1+∠2=180°.
(1)试说明:DG∥AC;
(2)若CD平分∠ACB,DG平分∠BDC,且∠A=40°,求∠ACB的度数.
六、(本题满分12分)
21.已知关于x的不等式组.
(1)当a=5时,求该不等式组的解集;
(2)若该不等式组的解集是空集(无解),求a的最小值;
(3)若该不等式组有且仅有3个整数解,则a的取值范围是 .
七、(本题满分12分)
22.【问题景】
多项式的乘法公式可以利用图形中面积的等量关系来验证其正确性.例如,(a+b)2=a2+2ab+b2就能利用图1的面积进行验证.
【问题解决】
(1)直接写出图2中所表示的等式: ;
(2)画出适当的图形,以表示等式(3x)2=9x2;
(3)利用图2中所表示的等式分解因式:
①3x2+4x+1= ;
②2m2+8mn+6n2= .
八、(本题满分14分)
23.超市分两次购进甲、乙两种商品若干件,进货总价如下表:
甲 乙
第一次 1200元 900元
第二次 总共不超过1262元
(1)第一次购进甲商品件数是乙商品件数的2倍,且甲商品的单价比乙商品的单价便宜10元/件,求甲商品的单价;
(2)第二次共购进50件,两种商品的单价与第一次相比,甲提高了10%,乙降价了10%,问此次最多购进乙商品多少件?
参考答案
一、选择题(共10小题,每小题4分,共40分).
1.下列实数中,属于无理数的是( )
A.﹣ B.3.14 C. D.
解:A、﹣是无理数,故本选项符合题意;
B、3.14是有限小数,属于有理数,故本选项不符合题意;
C、是分数,属于有理数,故本选项不符合题意;
D、=2,是整数,属于有理数,故本选项不符合题意;
故选:A.
2.如图,已知AC⊥BC,CD⊥AB于点D,表示点A到直线CD的距离的是( )
A.线段CD的长度 B.线段AC的长度
C.线段AD的长度 D.线段BC的长度
解:点A到CD的距离是线段AD的长度.
故选:C.
3.下列计算正确的是( )
A.a2+a3=a5 B.a2?a3=a6 C.(2a)3=6a3 D.(a2)3=a6
解:A、a2与a3不是同类项,故A不符合题意.
B、原式=a5,故B不符合题意.
C、原式=8a3,故C不符合题意.
D、原式=a6,故D符合题意.
故选:D.
4.若A(m2﹣3n)=m3﹣3mn,则代数式A的值为( )
A.m B.mn C.mn2 D.m2n
解:∵A(m2﹣3n)=m3﹣3mn=m(m2﹣3n),
∴A=m.
故选:A.
5.下列各式中,能运用完全平方公式分解因式的是( )
A.﹣x2﹣4 B.x2﹣4x+4 C.﹣x2+4x+4 D.4x2+4x+4
解:A、多项式﹣x2﹣4无法分解因式,故此选项不合题意;
B、多项式x2﹣4x+4=(x﹣2)2,故本选项符合题意;
C、多项式﹣x2+4x+4无法分解因式,故此选项不合题意;
D、多项式4x2+4x+4不是完全平方式,故此选项不合题意.
故选:B.
6.若x>y,下列不等式中一定成立的是( )
A.mx<my B.x2>y2 C.xc2>yc2 D.x﹣a>y﹣a
解:A、∵x>y,
∴当m=1时,mx>my,
∴选项A结论不一定成立;
B、∵x>y,
∴当x=2,y=﹣3时,x2<y2,
∴选项B结论不一定成立;
C、当c=0时,xc2=yc2,
∴选项C结论不一定成立;
D、∵x>y,
∴x﹣a>y﹣a,
∴选项D结论一定成立.
故选:D.
7.计算(x2+mx)(4x﹣8)的结果中不含x2项,则m的值是( )
A.﹣2 B.2 C.﹣1 D.1
解:(x2+mx)(4x﹣8)
=4x3﹣8x2+4mx2﹣8mx
=4x3+(4m﹣8)x2﹣8mx,
∵不含x2项,
∴4m﹣8=0,
∴m=2.
故选:B.
8.如图,下列条件能判定AD∥BC的是( )
A.∠MAD=∠D B.∠D=∠DCN
C.∠B=∠DCN D.∠B+∠BCD=180°
解:A、∵∠MAD=∠D,∴DC∥AB,故本选项错误,不符合题意;
B、∵∠D=∠DCN,∴AD∥BC,故本选项正确,符合题意;
C、∵∠B=∠DCN,∴DC∥AB,故本选项错误,不符合题意;
D、∵∠B+∠BCD=180°,∴DC∥AB,故本选项错误,不符合题意;
故选:B.
9.在一个长、宽、高分别为8cm,4cm,2cm的长方体容器中装满水,将容器中的水全部倒入一个正方体容器中,恰好倒满(两容器的厚度忽略不计),则此正方体容器的棱长是( )
A.2cm B.4cm C.6cm D.8cm
解:由于装满水的长方体,倒入正方体容器中,恰好倒满,
所以它们的体积相等,
设正方体棱长是acm,
则a?=8×4×2,
解得a=4.
故选:B.
10.若|x+y﹣5|+=0,则x2+y2的值为( )
A.19 B.31 C.27 D.23
解:根据题意得,x+y﹣5=0,xy﹣3=0,
∴x+y=5,xy=3,
∵(x+y)2=x2+2xy+y2=25,
∴x2+y2=25﹣2×3=25﹣6=19.
故选:A.
二、填空题(本大题共4小题,每小题5分,满分20分)
11.如图,AC⊥BC,直线EF经过点C,若∠1=37°,则∠2的度数是 53° .
解:∵AC⊥BC,
∴∠ACB=90°,
∵∠1+∠ACB+∠2=180°,
∴∠2=180°﹣90°﹣37°=53°,
故答案为:53°.
12.因式分解:3ax2﹣3ay2= 3a(x+y)(x﹣y) .
解:3ax2﹣3ay2=3a(x2﹣y2)=3a(x+y)(x﹣y).
故答案为:3a(x+y)(x﹣y)
13.如图,将周长为12cm的三角形ABC沿边BC向右平移5cm,得到三角形A′B′C′,则四边形AA′C′B的周长是 22 cm.
解:由平移的性质可知,A′C′=AC,AA′=BB′=5cm,B′C′=BC,
∵△ABC的周长为12cm,
∴AB+BC+AC=12(cm),
∴四边形AA'C'B的周长=AB+BC′+A′C′+A′A=AB+BB′+B′C′+A′C′+A′A=12+10=22(cm),
故答案为:22.
14.已知关于x的分式方程+=﹣2.
(1)如果该方程的解是x=2,那么m的值等于 1 ;
(2)如果该方程的解为正数,那么m的取值范围是 m<5且m≠3 .
解:(1)去分母得:﹣3+m=﹣2x+2,
∵该方程的解是x=2,
∴﹣3+m=﹣4+2,
解得:m=1;
故答案为1.
(2)去分母得:﹣3+m=﹣2x+2,
解方程﹣3+m=﹣2x+2,
得:x=,
根据分式方程的解为正数,得到>0,且≠1,
解得:m54且m≠3.
故答案为m<5且m≠3.
三、(本大题共2小题,每小题8分,满分16分)
15.计算:(π﹣2021)0+﹣()﹣2.
解:原式=1+4﹣9
=﹣4.
16.解不等式:﹣x≥﹣1.
解:,
x+3﹣3x≥﹣3,
x﹣3x≥﹣3﹣3,
﹣2x≥﹣6,
x≤3.
四、(本大题共2小题,每小题8分,满分16分)
17.已知x+7的平方根是±3,2x+y﹣13的立方根是1,求的值.
解:根据题意得:x+7=9,2x+y﹣13=1,
解得:x=2,y=10,
则==,
即的值是.
18.如图,在正方形网格中,每个小正方形的边长都为1个单位长度,线段AB的端点及点C都在格点(网格线交点)上.
(1)将线段AB向左平移2个单位长度、向上平移5个单位长度后得到线段A′B′,在图中画出线段A′B′;
(2)在图中画出经过点C且平行于AB的直线l,并简单的说明画法.
解:(1)如图,线段A′B′即为所求.
(2)如图,直线l即为所求.
作法:取格点T,作直线CT即可.
五、(本大题共2小题,每小题10分,满分20分)
19.已知代数式T=(x﹣2﹣)÷.
(1)化简T;
(2)当T2=9时,x= 5或﹣1 .
解:(1)T=
=
=
=x﹣2;
(2)当T2=9时,(x﹣2)2=9,
∴x﹣2=±3,
解得:x=5或x=﹣1,
故答案为:5或﹣1.
20.如图,已知EF∥CD,∠1+∠2=180°.
(1)试说明:DG∥AC;
(2)若CD平分∠ACB,DG平分∠BDC,且∠A=40°,求∠ACB的度数.
【解答】(1)证明:∵EF∥CD,
∴∠1+∠ECD=180°,
又∵∠1+∠2=180°,
∴∠2=∠ECD,
∴GD∥AC;
(2)解:由(1)得:GD∥AC,
∵∠A=40°,
∴∠BDG=∠A=40°,∠ACD=∠2,
∵DG平分∠BDC,
∴∠2=∠BDG=40°,
∴∠ACD=∠2=40°,
∵CD平分∠ACB,
∴∠ACB=2∠ACD=80°.
六、(本题满分12分)
21.已知关于x的不等式组.
(1)当a=5时,求该不等式组的解集;
(2)若该不等式组的解集是空集(无解),求a的最小值;
(3)若该不等式组有且仅有3个整数解,则a的取值范围是 21≤a≤25 .
解:(1),
解不等式①,得x<9,
当a=5时,4x+1>5,
解得:x>1,
所以不等式组的解集是1<x<9;
(2)解不等式①,得x<9,
解不等式②,得x>,
∵该不等式组的解集是空集,
∴≥9,
解得:a≥37,
∴a的最小值是37;
(3)∵不等式①的解集是x<9,不等式②的解集是x>,
又∵该不等式组有且仅有3个整数解(整数解是6,7,8)
∴5≤<6,
解得:21≤a≤25,
故答案为:21≤a≤25.
七、(本题满分12分)
22.【问题景】
多项式的乘法公式可以利用图形中面积的等量关系来验证其正确性.例如,(a+b)2=a2+2ab+b2就能利用图1的面积进行验证.
【问题解决】
(1)直接写出图2中所表示的等式: (a+b)(3a+b)=3a2+4ab+b2 ;
(2)画出适当的图形,以表示等式(3x)2=9x2;
(3)利用图2中所表示的等式分解因式:
①3x2+4x+1= (3x+1)(x+1) ;
②2m2+8mn+6n2= 2(m+n)(m+3n) .
解:(1)观察图2,从总体来看,大矩形的长为:3a+b,宽为:a+b,
∴大矩形面积可表示为:(a+b)(3a+b);
从局部来看,各小矩形的面积依次相加,可得:a2+ab+ab+a2+b2+ab+a2+ab=3a2+4ab+b2;
故答案为:(a+b)(3a+b)=3a2+4ab+b2;
(2)
如上图,从整体来看:3x?3x=(3x)2,从局部来看:9?x2=9x2,
∴(3x)2=9x2;
(3)①3x2+4x+1=(3x+1)(x+1),
②2m2+8mn+6n2=(2m+2n)(m+3n)=2(m+n)(m+3n),
故答案为:(3x+1)(x+1),2(m+n)(m+3n).
八、(本题满分14分)
23.超市分两次购进甲、乙两种商品若干件,进货总价如下表:
甲 乙
第一次 1200元 900元
第二次 总共不超过1262元
(1)第一次购进甲商品件数是乙商品件数的2倍,且甲商品的单价比乙商品的单价便宜10元/件,求甲商品的单价;
(2)第二次共购进50件,两种商品的单价与第一次相比,甲提高了10%,乙降价了10%,问此次最多购进乙商品多少件?
解:(1)设甲商品的单价为x元,则乙商品的单价为(x+10)元,
依题意得:=2×,
解得:x=20,
经检验,x=20是原方程的解,且符合题意.
答:甲商品的单价为20元.
(2)设购进乙商品m件,则购进甲商品(50﹣m)件,
依题意得:20×(1+10%)(50﹣m)+(20+10)×(1﹣10%)m≤1262,
解得:m≤32.
又∵m为整数,
∴m的最大值为32.
答:此次最多购进乙商品32件.
一、选择题(共10小题,每小题4分,共40分).
1.下列实数中,属于无理数的是( )
A.﹣ B.3.14 C. D.
2.如图,已知AC⊥BC,CD⊥AB于点D,表示点A到直线CD的距离的是( )
A.线段CD的长度 B.线段AC的长度
C.线段AD的长度 D.线段BC的长度
3.下列计算正确的是( )
A.a2+a3=a5 B.a2?a3=a6 C.(2a)3=6a3 D.(a2)3=a6
4.若A(m2﹣3n)=m3﹣3mn,则代数式A的值为( )
A.m B.mn C.mn2 D.m2n
5.下列各式中,能运用完全平方公式分解因式的是( )
A.﹣x2﹣4 B.x2﹣4x+4 C.﹣x2+4x+4 D.4x2+4x+4
6.若x>y,下列不等式中一定成立的是( )
A.mx<my B.x2>y2 C.xc2>yc2 D.x﹣a>y﹣a
7.计算(x2+mx)(4x﹣8)的结果中不含x2项,则m的值是( )
A.﹣2 B.2 C.﹣1 D.1
8.如图,下列条件能判定AD∥BC的是( )
A.∠MAD=∠D B.∠D=∠DCN
C.∠B=∠DCN D.∠B+∠BCD=180°
9.在一个长、宽、高分别为8cm,4cm,2cm的长方体容器中装满水,将容器中的水全部倒入一个正方体容器中,恰好倒满(两容器的厚度忽略不计),则此正方体容器的棱长是( )
A.2cm B.4cm C.6cm D.8cm
10.若|x+y﹣5|+=0,则x2+y2的值为( )
A.19 B.31 C.27 D.23
二、填空题(本大题共4小题,每小题5分,满分20分)
11.如图,AC⊥BC,直线EF经过点C,若∠1=37°,则∠2的度数是 .
12.因式分解:3ax2﹣3ay2= .
13.如图,将周长为12cm的三角形ABC沿边BC向右平移5cm,得到三角形A′B′C′,则四边形AA′C′B的周长是 cm.
14.已知关于x的分式方程+=﹣2.
(1)如果该方程的解是x=2,那么m的值等于 ;
(2)如果该方程的解为正数,那么m的取值范围是 .
三、(本大题共2小题,每小题8分,满分16分)
15.计算:(π﹣2021)0+﹣()﹣2.
16.解不等式:﹣x≥﹣1.
四、(本大题共2小题,每小题8分,满分16分)
17.已知x+7的平方根是±3,2x+y﹣13的立方根是1,求的值.
18.如图,在正方形网格中,每个小正方形的边长都为1个单位长度,线段AB的端点及点C都在格点(网格线交点)上.
(1)将线段AB向左平移2个单位长度、向上平移5个单位长度后得到线段A′B′,在图中画出线段A′B′;
(2)在图中画出经过点C且平行于AB的直线l,并简单的说明画法.
五、(本大题共2小题,每小题10分,满分20分)
19.已知代数式T=(x﹣2﹣)÷.
(1)化简T;
(2)当T2=9时,x= .
20.如图,已知EF∥CD,∠1+∠2=180°.
(1)试说明:DG∥AC;
(2)若CD平分∠ACB,DG平分∠BDC,且∠A=40°,求∠ACB的度数.
六、(本题满分12分)
21.已知关于x的不等式组.
(1)当a=5时,求该不等式组的解集;
(2)若该不等式组的解集是空集(无解),求a的最小值;
(3)若该不等式组有且仅有3个整数解,则a的取值范围是 .
七、(本题满分12分)
22.【问题景】
多项式的乘法公式可以利用图形中面积的等量关系来验证其正确性.例如,(a+b)2=a2+2ab+b2就能利用图1的面积进行验证.
【问题解决】
(1)直接写出图2中所表示的等式: ;
(2)画出适当的图形,以表示等式(3x)2=9x2;
(3)利用图2中所表示的等式分解因式:
①3x2+4x+1= ;
②2m2+8mn+6n2= .
八、(本题满分14分)
23.超市分两次购进甲、乙两种商品若干件,进货总价如下表:
甲 乙
第一次 1200元 900元
第二次 总共不超过1262元
(1)第一次购进甲商品件数是乙商品件数的2倍,且甲商品的单价比乙商品的单价便宜10元/件,求甲商品的单价;
(2)第二次共购进50件,两种商品的单价与第一次相比,甲提高了10%,乙降价了10%,问此次最多购进乙商品多少件?
参考答案
一、选择题(共10小题,每小题4分,共40分).
1.下列实数中,属于无理数的是( )
A.﹣ B.3.14 C. D.
解:A、﹣是无理数,故本选项符合题意;
B、3.14是有限小数,属于有理数,故本选项不符合题意;
C、是分数,属于有理数,故本选项不符合题意;
D、=2,是整数,属于有理数,故本选项不符合题意;
故选:A.
2.如图,已知AC⊥BC,CD⊥AB于点D,表示点A到直线CD的距离的是( )
A.线段CD的长度 B.线段AC的长度
C.线段AD的长度 D.线段BC的长度
解:点A到CD的距离是线段AD的长度.
故选:C.
3.下列计算正确的是( )
A.a2+a3=a5 B.a2?a3=a6 C.(2a)3=6a3 D.(a2)3=a6
解:A、a2与a3不是同类项,故A不符合题意.
B、原式=a5,故B不符合题意.
C、原式=8a3,故C不符合题意.
D、原式=a6,故D符合题意.
故选:D.
4.若A(m2﹣3n)=m3﹣3mn,则代数式A的值为( )
A.m B.mn C.mn2 D.m2n
解:∵A(m2﹣3n)=m3﹣3mn=m(m2﹣3n),
∴A=m.
故选:A.
5.下列各式中,能运用完全平方公式分解因式的是( )
A.﹣x2﹣4 B.x2﹣4x+4 C.﹣x2+4x+4 D.4x2+4x+4
解:A、多项式﹣x2﹣4无法分解因式,故此选项不合题意;
B、多项式x2﹣4x+4=(x﹣2)2,故本选项符合题意;
C、多项式﹣x2+4x+4无法分解因式,故此选项不合题意;
D、多项式4x2+4x+4不是完全平方式,故此选项不合题意.
故选:B.
6.若x>y,下列不等式中一定成立的是( )
A.mx<my B.x2>y2 C.xc2>yc2 D.x﹣a>y﹣a
解:A、∵x>y,
∴当m=1时,mx>my,
∴选项A结论不一定成立;
B、∵x>y,
∴当x=2,y=﹣3时,x2<y2,
∴选项B结论不一定成立;
C、当c=0时,xc2=yc2,
∴选项C结论不一定成立;
D、∵x>y,
∴x﹣a>y﹣a,
∴选项D结论一定成立.
故选:D.
7.计算(x2+mx)(4x﹣8)的结果中不含x2项,则m的值是( )
A.﹣2 B.2 C.﹣1 D.1
解:(x2+mx)(4x﹣8)
=4x3﹣8x2+4mx2﹣8mx
=4x3+(4m﹣8)x2﹣8mx,
∵不含x2项,
∴4m﹣8=0,
∴m=2.
故选:B.
8.如图,下列条件能判定AD∥BC的是( )
A.∠MAD=∠D B.∠D=∠DCN
C.∠B=∠DCN D.∠B+∠BCD=180°
解:A、∵∠MAD=∠D,∴DC∥AB,故本选项错误,不符合题意;
B、∵∠D=∠DCN,∴AD∥BC,故本选项正确,符合题意;
C、∵∠B=∠DCN,∴DC∥AB,故本选项错误,不符合题意;
D、∵∠B+∠BCD=180°,∴DC∥AB,故本选项错误,不符合题意;
故选:B.
9.在一个长、宽、高分别为8cm,4cm,2cm的长方体容器中装满水,将容器中的水全部倒入一个正方体容器中,恰好倒满(两容器的厚度忽略不计),则此正方体容器的棱长是( )
A.2cm B.4cm C.6cm D.8cm
解:由于装满水的长方体,倒入正方体容器中,恰好倒满,
所以它们的体积相等,
设正方体棱长是acm,
则a?=8×4×2,
解得a=4.
故选:B.
10.若|x+y﹣5|+=0,则x2+y2的值为( )
A.19 B.31 C.27 D.23
解:根据题意得,x+y﹣5=0,xy﹣3=0,
∴x+y=5,xy=3,
∵(x+y)2=x2+2xy+y2=25,
∴x2+y2=25﹣2×3=25﹣6=19.
故选:A.
二、填空题(本大题共4小题,每小题5分,满分20分)
11.如图,AC⊥BC,直线EF经过点C,若∠1=37°,则∠2的度数是 53° .
解:∵AC⊥BC,
∴∠ACB=90°,
∵∠1+∠ACB+∠2=180°,
∴∠2=180°﹣90°﹣37°=53°,
故答案为:53°.
12.因式分解:3ax2﹣3ay2= 3a(x+y)(x﹣y) .
解:3ax2﹣3ay2=3a(x2﹣y2)=3a(x+y)(x﹣y).
故答案为:3a(x+y)(x﹣y)
13.如图,将周长为12cm的三角形ABC沿边BC向右平移5cm,得到三角形A′B′C′,则四边形AA′C′B的周长是 22 cm.
解:由平移的性质可知,A′C′=AC,AA′=BB′=5cm,B′C′=BC,
∵△ABC的周长为12cm,
∴AB+BC+AC=12(cm),
∴四边形AA'C'B的周长=AB+BC′+A′C′+A′A=AB+BB′+B′C′+A′C′+A′A=12+10=22(cm),
故答案为:22.
14.已知关于x的分式方程+=﹣2.
(1)如果该方程的解是x=2,那么m的值等于 1 ;
(2)如果该方程的解为正数,那么m的取值范围是 m<5且m≠3 .
解:(1)去分母得:﹣3+m=﹣2x+2,
∵该方程的解是x=2,
∴﹣3+m=﹣4+2,
解得:m=1;
故答案为1.
(2)去分母得:﹣3+m=﹣2x+2,
解方程﹣3+m=﹣2x+2,
得:x=,
根据分式方程的解为正数,得到>0,且≠1,
解得:m54且m≠3.
故答案为m<5且m≠3.
三、(本大题共2小题,每小题8分,满分16分)
15.计算:(π﹣2021)0+﹣()﹣2.
解:原式=1+4﹣9
=﹣4.
16.解不等式:﹣x≥﹣1.
解:,
x+3﹣3x≥﹣3,
x﹣3x≥﹣3﹣3,
﹣2x≥﹣6,
x≤3.
四、(本大题共2小题,每小题8分,满分16分)
17.已知x+7的平方根是±3,2x+y﹣13的立方根是1,求的值.
解:根据题意得:x+7=9,2x+y﹣13=1,
解得:x=2,y=10,
则==,
即的值是.
18.如图,在正方形网格中,每个小正方形的边长都为1个单位长度,线段AB的端点及点C都在格点(网格线交点)上.
(1)将线段AB向左平移2个单位长度、向上平移5个单位长度后得到线段A′B′,在图中画出线段A′B′;
(2)在图中画出经过点C且平行于AB的直线l,并简单的说明画法.
解:(1)如图,线段A′B′即为所求.
(2)如图,直线l即为所求.
作法:取格点T,作直线CT即可.
五、(本大题共2小题,每小题10分,满分20分)
19.已知代数式T=(x﹣2﹣)÷.
(1)化简T;
(2)当T2=9时,x= 5或﹣1 .
解:(1)T=
=
=
=x﹣2;
(2)当T2=9时,(x﹣2)2=9,
∴x﹣2=±3,
解得:x=5或x=﹣1,
故答案为:5或﹣1.
20.如图,已知EF∥CD,∠1+∠2=180°.
(1)试说明:DG∥AC;
(2)若CD平分∠ACB,DG平分∠BDC,且∠A=40°,求∠ACB的度数.
【解答】(1)证明:∵EF∥CD,
∴∠1+∠ECD=180°,
又∵∠1+∠2=180°,
∴∠2=∠ECD,
∴GD∥AC;
(2)解:由(1)得:GD∥AC,
∵∠A=40°,
∴∠BDG=∠A=40°,∠ACD=∠2,
∵DG平分∠BDC,
∴∠2=∠BDG=40°,
∴∠ACD=∠2=40°,
∵CD平分∠ACB,
∴∠ACB=2∠ACD=80°.
六、(本题满分12分)
21.已知关于x的不等式组.
(1)当a=5时,求该不等式组的解集;
(2)若该不等式组的解集是空集(无解),求a的最小值;
(3)若该不等式组有且仅有3个整数解,则a的取值范围是 21≤a≤25 .
解:(1),
解不等式①,得x<9,
当a=5时,4x+1>5,
解得:x>1,
所以不等式组的解集是1<x<9;
(2)解不等式①,得x<9,
解不等式②,得x>,
∵该不等式组的解集是空集,
∴≥9,
解得:a≥37,
∴a的最小值是37;
(3)∵不等式①的解集是x<9,不等式②的解集是x>,
又∵该不等式组有且仅有3个整数解(整数解是6,7,8)
∴5≤<6,
解得:21≤a≤25,
故答案为:21≤a≤25.
七、(本题满分12分)
22.【问题景】
多项式的乘法公式可以利用图形中面积的等量关系来验证其正确性.例如,(a+b)2=a2+2ab+b2就能利用图1的面积进行验证.
【问题解决】
(1)直接写出图2中所表示的等式: (a+b)(3a+b)=3a2+4ab+b2 ;
(2)画出适当的图形,以表示等式(3x)2=9x2;
(3)利用图2中所表示的等式分解因式:
①3x2+4x+1= (3x+1)(x+1) ;
②2m2+8mn+6n2= 2(m+n)(m+3n) .
解:(1)观察图2,从总体来看,大矩形的长为:3a+b,宽为:a+b,
∴大矩形面积可表示为:(a+b)(3a+b);
从局部来看,各小矩形的面积依次相加,可得:a2+ab+ab+a2+b2+ab+a2+ab=3a2+4ab+b2;
故答案为:(a+b)(3a+b)=3a2+4ab+b2;
(2)
如上图,从整体来看:3x?3x=(3x)2,从局部来看:9?x2=9x2,
∴(3x)2=9x2;
(3)①3x2+4x+1=(3x+1)(x+1),
②2m2+8mn+6n2=(2m+2n)(m+3n)=2(m+n)(m+3n),
故答案为:(3x+1)(x+1),2(m+n)(m+3n).
八、(本题满分14分)
23.超市分两次购进甲、乙两种商品若干件,进货总价如下表:
甲 乙
第一次 1200元 900元
第二次 总共不超过1262元
(1)第一次购进甲商品件数是乙商品件数的2倍,且甲商品的单价比乙商品的单价便宜10元/件,求甲商品的单价;
(2)第二次共购进50件,两种商品的单价与第一次相比,甲提高了10%,乙降价了10%,问此次最多购进乙商品多少件?
解:(1)设甲商品的单价为x元,则乙商品的单价为(x+10)元,
依题意得:=2×,
解得:x=20,
经检验,x=20是原方程的解,且符合题意.
答:甲商品的单价为20元.
(2)设购进乙商品m件,则购进甲商品(50﹣m)件,
依题意得:20×(1+10%)(50﹣m)+(20+10)×(1﹣10%)m≤1262,
解得:m≤32.
又∵m为整数,
∴m的最大值为32.
答:此次最多购进乙商品32件.
同课章节目录
