江苏省宿迁市四校联考2019-2020学年高一下学期期末数学试卷Word无答案
文档属性
| 名称 | 江苏省宿迁市四校联考2019-2020学年高一下学期期末数学试卷Word无答案 |  | |
| 格式 | docx | ||
| 文件大小 | 77.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-01 08:16:03 | ||
图片预览

文档简介
2019-2020学年江苏省宿迁市四校联考高一(下)期末数学试卷
一.选择题(共8小题,满分40分,每小题5分)
1.甲、乙、丙三人随机排成一排,乙站在中间的概率是( )
A.
B.
C.
D.
2.将一个样本容量为100的数据分组,各组的频数如下:[17,19),1;[19,21),1;[21,23),3;[23,25),3;[25,27),18;[27,29),16;[29,31),28;[31,33],30.根据样本频率分布,估计小于29的数据大约占总体的( )
A.58%
B.42%
C.40%
D.16%
3.已知△ABC中,a,b,c分别是角A,B,C的对边,且满足bcosC=a+ccosB,则该三角形的形状是( )
A.等腰三角形
B.直角三角形
C.等边三角形
D.等腰或直角三角形
4.已知,且,,则( )
A.
B.
C.
D.
5.已知m,l是两条不重合的直线,α,β,γ是三个不重合的平面,则下列结论正确的是( )
A.若m∥l,α∥β,m与α相交,则l与β也相交
B.若α⊥β,β⊥γ,则α⊥γ
C.若α∥β,m与α所成角等于l与β所成角,则m∥l
D.若m⊥α,α⊥β,m?β,则m∥β
6.已知直角三角形ABC中,∠A=90°,AB=2,AC=4,点P在以A为圆心且与边BC相切的圆上,则的最大值为( )
A.
B.
C.
D.
7.在直三棱柱ABC﹣A1B1C1中,AB=2,AC,∠BAC=30°,AA1,则其外接球的体积是( )
A.
B.
C.
D.
8.若轴截面为正方形的圆柱内接于半径为1的球,则该圆柱的体积为( )
A.
B.
C.
D.
二.多选题(共4小题,满分20分,每小题5分)
9.下列说法中错误的是( )
A.若向最满足,则存在唯一的实数λ,使得
B.已知非零向,且与的夹角为锐角,则实数λ的取值范围是
C.“a≠1”是“复数z=(a﹣1)+(a2﹣1)i(a∈R)是虚数”的必要不充分条件
D.若复数z1,z2,满足z12﹣z22>0,则z12>z22
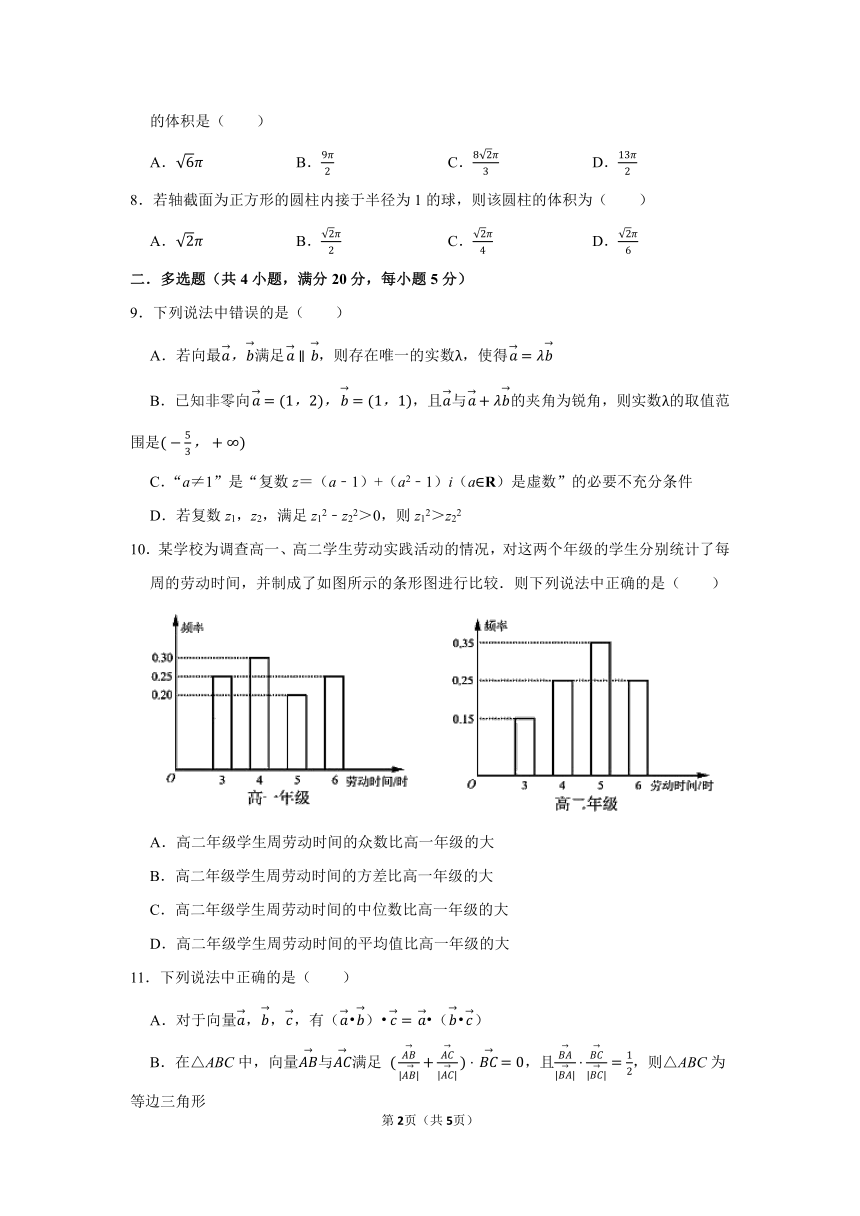
10.某学校为调查高一、高二学生劳动实践活动的情况,对这两个年级的学生分别统计了每周的劳动时间,并制成了如图所示的条形图进行比较.则下列说法中正确的是( )
A.高二年级学生周劳动时间的众数比高一年级的大
B.高二年级学生周劳动时间的方差比高一年级的大
C.高二年级学生周劳动时间的中位数比高一年级的大
D.高二年级学生周劳动时间的平均值比高一年级的大
11.下列说法中正确的是( )
A.对于向量,,,有(?)??(?)
B.在△ABC中,向量与满足
,且,则△ABC为等边三角形
C.若2,S△AOC,S△ABC分别表示△AOC,△ABC的面积,则S△AOC:S△ABC=1:6
D.在△ABC中,设D是BC边上一点,且满足,则λ+μ=0
12.如图,在菱形ABCD中,AB=2,∠ABC=60°,M为BC的中点,将△ABM沿直线AM翻折成△AB1M,连接B1C和B1D,N为B1D的中点,则在翻折过程中,下列说法正确的是( )
A.AM⊥B1C
B.CN的长不为定值
C.AB1与CN的夹角为
D.当三棱锥B1﹣AMD的体积最大时,三棱锥B1﹣AMD的外接球的表面积是12π
三.填空题(共4小题,满分20分,每小题5分)
13.甲、乙两名同学进行篮球投篮练习,甲同学一次投篮命中的概率为,乙同学一次投篮命中的概率为,假设两人投篮命中与否互不影响,则甲、乙两人各投篮一次,至少有一人命中的概率是
.
14.若,则sin(30°﹣2α)=
.
15.为美化环境,某小区计划将一片扇形区域改造为一个绿化区兼休闲娱乐区,如图所示,该扇形区域的圆心角为120°,OA=10m,在OA上选一点M,在弧上选一点N,使得MN∥OB,计划在点O处建休闲区,在点N处建健身区,并修建小路OM,MN,则|OM|+|MN|的最大值为
m.
16.三棱台ABC﹣A1B1C1中,AB:A1B1=1:2,则三棱锥A1﹣ABC,B﹣A1B1C,C﹣A1B1C1的体积之比是
.
四.解答题(共6小题,满分70分)
17.已知不共线的向量,满足||=3,||=2,,的夹角为θ.
(1)θ=30°,求||的值;
(2)若(2)⊥(),求cosθ的值
18.若复数|z﹣3i|=5,求|z+2|的最大值和最小值.
19.已知函数,再从条件①、条件②、条件③这三个条件中选择一个作为已知,求:
(Ⅰ)f(x)的单调递增区间;
(Ⅱ)f(x)在区间的取值范围.
条件①:;
条件②:f(x)=h(x)?g(x);
条件③:f(x)=h(x)﹣g(x).
20.某市的教育主管部门对所管辖的学校进行年终督导评估,为了解某学校师生对学校教学管的满意度,分别从教师和不同年级的同学中随机抽取若干师生,进行评分(满分100分),绘制如图频率分布直方图(分组区间为[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]),并将分数从低到高分为四个等级:
满意度评分
[0,60)
[60,80)
[80,90)
[90,100]
满意度等级
不满意
基本满意
满意
非常满意
已知满意度等级为基本满意的有340人.
(1)求表中a的值及不满意的人数;
(2)记A表示事件“满意度评分不低于80分”,估计A的概率;
(3)若师生的满意指数不低于0.8,则该校可获评“教学管理先进单位”.根据你所学的统计知识,判断该校是否能获评“教学管理先进单位”?并说明理由.(注:满意指数η)
21.如图,在四棱锥P﹣ABCD中,AD=BD=BC=1,,PA=PB,平面PBD⊥平面ABCD.
(1)求证:PD⊥AB;
(2)已知二面角P﹣AC﹣D的余弦值为.线段PC上是否存在点M,使得BM与平面PAC所成的角为30°?证明你的结论.
22.在△ABC中,角A,B,C的对边分别是a,b,c,已知a?sinA+a?sinC?cosB+b?sinC?cosA=b?sinB+c?sinA.
(1)求角B的大小;
(2)若b=3,c=3,点D满足,求△ABD的面积.
第1页(共3页)
一.选择题(共8小题,满分40分,每小题5分)
1.甲、乙、丙三人随机排成一排,乙站在中间的概率是( )
A.
B.
C.
D.
2.将一个样本容量为100的数据分组,各组的频数如下:[17,19),1;[19,21),1;[21,23),3;[23,25),3;[25,27),18;[27,29),16;[29,31),28;[31,33],30.根据样本频率分布,估计小于29的数据大约占总体的( )
A.58%
B.42%
C.40%
D.16%
3.已知△ABC中,a,b,c分别是角A,B,C的对边,且满足bcosC=a+ccosB,则该三角形的形状是( )
A.等腰三角形
B.直角三角形
C.等边三角形
D.等腰或直角三角形
4.已知,且,,则( )
A.
B.
C.
D.
5.已知m,l是两条不重合的直线,α,β,γ是三个不重合的平面,则下列结论正确的是( )
A.若m∥l,α∥β,m与α相交,则l与β也相交
B.若α⊥β,β⊥γ,则α⊥γ
C.若α∥β,m与α所成角等于l与β所成角,则m∥l
D.若m⊥α,α⊥β,m?β,则m∥β
6.已知直角三角形ABC中,∠A=90°,AB=2,AC=4,点P在以A为圆心且与边BC相切的圆上,则的最大值为( )
A.
B.
C.
D.
7.在直三棱柱ABC﹣A1B1C1中,AB=2,AC,∠BAC=30°,AA1,则其外接球的体积是( )
A.
B.
C.
D.
8.若轴截面为正方形的圆柱内接于半径为1的球,则该圆柱的体积为( )
A.
B.
C.
D.
二.多选题(共4小题,满分20分,每小题5分)
9.下列说法中错误的是( )
A.若向最满足,则存在唯一的实数λ,使得
B.已知非零向,且与的夹角为锐角,则实数λ的取值范围是
C.“a≠1”是“复数z=(a﹣1)+(a2﹣1)i(a∈R)是虚数”的必要不充分条件
D.若复数z1,z2,满足z12﹣z22>0,则z12>z22
10.某学校为调查高一、高二学生劳动实践活动的情况,对这两个年级的学生分别统计了每周的劳动时间,并制成了如图所示的条形图进行比较.则下列说法中正确的是( )
A.高二年级学生周劳动时间的众数比高一年级的大
B.高二年级学生周劳动时间的方差比高一年级的大
C.高二年级学生周劳动时间的中位数比高一年级的大
D.高二年级学生周劳动时间的平均值比高一年级的大
11.下列说法中正确的是( )
A.对于向量,,,有(?)??(?)
B.在△ABC中,向量与满足
,且,则△ABC为等边三角形
C.若2,S△AOC,S△ABC分别表示△AOC,△ABC的面积,则S△AOC:S△ABC=1:6
D.在△ABC中,设D是BC边上一点,且满足,则λ+μ=0
12.如图,在菱形ABCD中,AB=2,∠ABC=60°,M为BC的中点,将△ABM沿直线AM翻折成△AB1M,连接B1C和B1D,N为B1D的中点,则在翻折过程中,下列说法正确的是( )
A.AM⊥B1C
B.CN的长不为定值
C.AB1与CN的夹角为
D.当三棱锥B1﹣AMD的体积最大时,三棱锥B1﹣AMD的外接球的表面积是12π
三.填空题(共4小题,满分20分,每小题5分)
13.甲、乙两名同学进行篮球投篮练习,甲同学一次投篮命中的概率为,乙同学一次投篮命中的概率为,假设两人投篮命中与否互不影响,则甲、乙两人各投篮一次,至少有一人命中的概率是
.
14.若,则sin(30°﹣2α)=
.
15.为美化环境,某小区计划将一片扇形区域改造为一个绿化区兼休闲娱乐区,如图所示,该扇形区域的圆心角为120°,OA=10m,在OA上选一点M,在弧上选一点N,使得MN∥OB,计划在点O处建休闲区,在点N处建健身区,并修建小路OM,MN,则|OM|+|MN|的最大值为
m.
16.三棱台ABC﹣A1B1C1中,AB:A1B1=1:2,则三棱锥A1﹣ABC,B﹣A1B1C,C﹣A1B1C1的体积之比是
.
四.解答题(共6小题,满分70分)
17.已知不共线的向量,满足||=3,||=2,,的夹角为θ.
(1)θ=30°,求||的值;
(2)若(2)⊥(),求cosθ的值
18.若复数|z﹣3i|=5,求|z+2|的最大值和最小值.
19.已知函数,再从条件①、条件②、条件③这三个条件中选择一个作为已知,求:
(Ⅰ)f(x)的单调递增区间;
(Ⅱ)f(x)在区间的取值范围.
条件①:;
条件②:f(x)=h(x)?g(x);
条件③:f(x)=h(x)﹣g(x).
20.某市的教育主管部门对所管辖的学校进行年终督导评估,为了解某学校师生对学校教学管的满意度,分别从教师和不同年级的同学中随机抽取若干师生,进行评分(满分100分),绘制如图频率分布直方图(分组区间为[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]),并将分数从低到高分为四个等级:
满意度评分
[0,60)
[60,80)
[80,90)
[90,100]
满意度等级
不满意
基本满意
满意
非常满意
已知满意度等级为基本满意的有340人.
(1)求表中a的值及不满意的人数;
(2)记A表示事件“满意度评分不低于80分”,估计A的概率;
(3)若师生的满意指数不低于0.8,则该校可获评“教学管理先进单位”.根据你所学的统计知识,判断该校是否能获评“教学管理先进单位”?并说明理由.(注:满意指数η)
21.如图,在四棱锥P﹣ABCD中,AD=BD=BC=1,,PA=PB,平面PBD⊥平面ABCD.
(1)求证:PD⊥AB;
(2)已知二面角P﹣AC﹣D的余弦值为.线段PC上是否存在点M,使得BM与平面PAC所成的角为30°?证明你的结论.
22.在△ABC中,角A,B,C的对边分别是a,b,c,已知a?sinA+a?sinC?cosB+b?sinC?cosA=b?sinB+c?sinA.
(1)求角B的大小;
(2)若b=3,c=3,点D满足,求△ABD的面积.
第1页(共3页)
同课章节目录
