6.1-6.3 余角 补角 对顶角同步训练(含解析)
文档属性
| 名称 | 6.1-6.3 余角 补角 对顶角同步训练(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 261.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-31 00:00:00 | ||
图片预览



文档简介
初中数学苏科版七年级上册6.1-6.3 同步练习
一、单选题
1.在下列日常生活的操作中,能体现基本事实“两点之间,线段最短”的是(?????? )
A.?用两颗钉子可以固定一根木条 B.?把弯路改直可以缩短路程
C.?用两根木桩拉一直线可把树栽成一排 D.?沿桌子的一边看,可将桌子排整齐
2.如图是一副三角板摆成的图形,如果 ∠AOB=160° ,那么 ∠COD 等于(?? )
A.?15°???????????????????????????????????????B.?20°???????????????????????????????????????C.?30°???????????????????????????????????????D.?40°
3.如图,数轴的单位长度为1,如果点 A 表示的数为-2,那么点 B 表示的数是(?? ).
A.?-1???????????????????????????????????????????B.?0???????????????????????????????????????????C.?3???????????????????????????????????????????D.?4
4.如图, ∠AOB=60° ,以 OA 为一边作 ∠AOC=15° ,则 ∠BOC 的度数为(?? )
A.?15°???????????????????????????B.?45°???????????????????????????C.?15° 或 75°???????????????????????????D.?45° 或 75°
5.将一副直角三角尺按如图所示摆放,则图中 ∠ABC 的度数是(?? )
A.?105°????????????????????????????????????B.?120°????????????????????????????????????C.?135°????????????????????????????????????D.?150°
6.如图,直线AB和CD相交于O,那么图中 ∠DOE与∠COA? 的关系是(?? )
A.?对顶角????????????????????????????????????B.?相等????????????????????????????????????C.?互余????????????????????????????????????D.?互补
7.如图,下列说法中错误的是(?? ).
A.?OA 方向是北偏东20° B.?OB 方向是北偏西15°
C.?OC 方向是南偏西30° D.?OD 方向是东南方向
8.在下图中,∠1和∠2是对顶角的是(?? )
A.??????????????B.? ??C.??????????????D.?
9.现实生活中“为何有人宁可违反交通规则翻越隔离带乱穿马路,也不愿从天桥或斑马线通过?”,请用数学知识解释这一现象,其原因为( ??)
A.?两点之间线段的长度,叫做这两点之间的距离????B.?过一点有无数条直线
C.?两点确定一条直线??????????????????????????????????????????????D.?两点之间,线段最短
10.已知:如图,AB⊥CD,垂足为O,EF为过点O的一条直线,则∠1与∠2的关系一定成立的是(?? ?)
A.?相等????????????????????????????????????B.?互余????????????????????????????????????C.?互补????????????????????????????????????D.?不确定
二、填空题
11.已知 ∠α=68°42' .则 ∠α 的余角为________.
12.若 ∠A=34° ,则 ∠A 的补角等于________.
13.钟表上显示6时20分,则此刻时针与分针的夹角的度数为________.
14.如图,直线 a 、 b 相交于点 O ,将量角器的中心与点 O 重合,发现表示 60° 的点在直线 a 上,表示 135° 的点在直线 b 上,则 ∠1= ________ ° .
15.如图,将一个三角板 60° 角的顶点与另一个三角板的直角顶点重合, ∠1=28° , ∠2=________° .
16.如图,∠1=30°,则射线OA表示的方位是南偏东________.
17.从甲地到乙地有3条路,但小明说这三条路都不是最短的,小明的依据是________.
18.下列生产和生活现象:①用两个钉子就可以把木条固定在墙上;②把弯曲的公路改直,就能缩短路程;③植树时,只要确定两棵树的位置,就能确定同一行树所在的直线;④从 A 地到 B 地架设电线,总是尽可能沿着线段 AB 架设.其中能用“两点之间,线段最短”来解释的现象有________.(填序号)
19.如图,直线 AB , CD 相交于点 O , OE⊥CD ,垂足为点 O ,若 ∠BOE=40° ,则 ∠AOC 的度数为________.
20.“数形结合”思想在数轴上得到充分体现,如在数轴上表示数5和 ?2 的两点之间的距离,可列式表示为 |5?(?2)| ,或 |?2?5| ;表示数 x 和 ?3 的两点之间的距离可列式表示为 |x?(?3)|=|x+3| .已知 |x+3|+|x?1|+|y+2|+|y?3|=9 ,则 x+y 的最大值为________.
三、解答题
21.一个角的余角比它的补角的 12 还少15°,求这个角的度数.
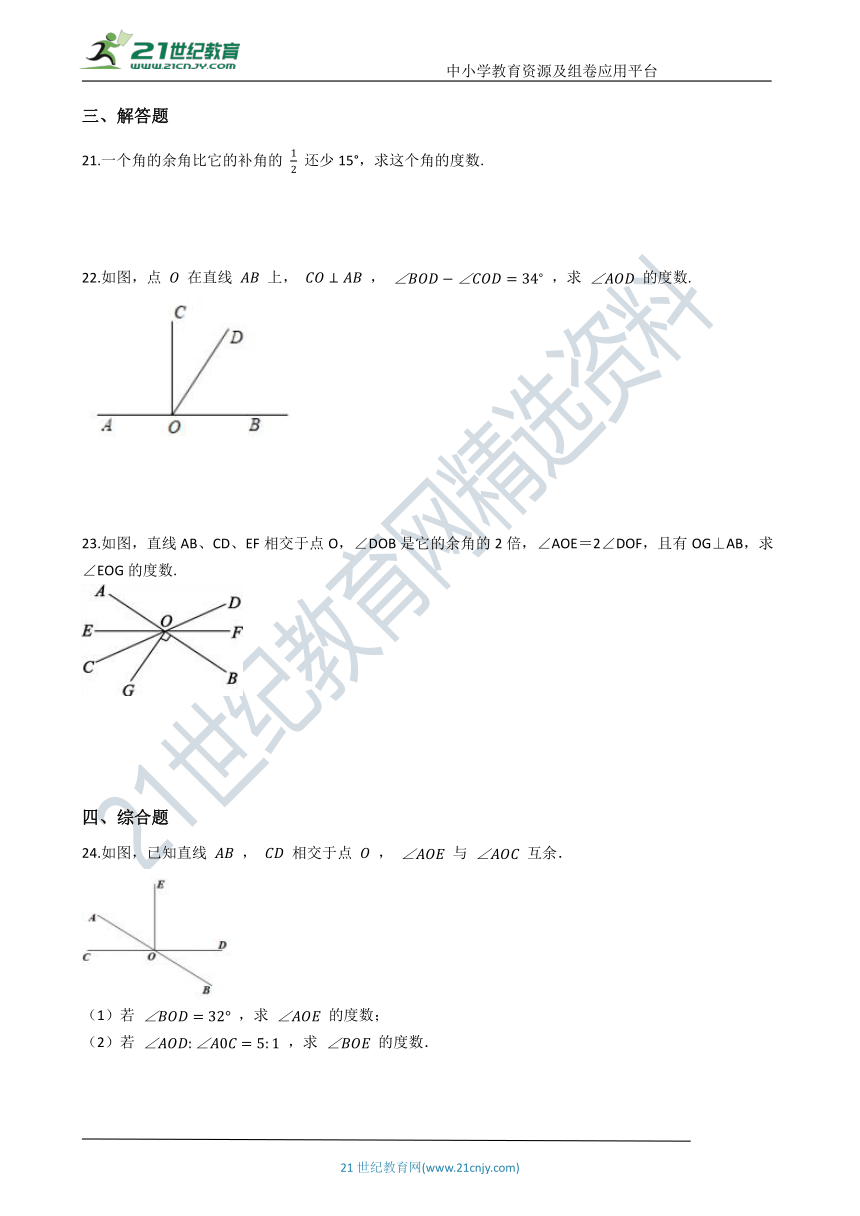
22.如图,点 O 在直线 AB 上, CO⊥AB , ∠BOD?∠COD=34? ,求 ∠AOD 的度数.
23.如图,直线AB、CD、EF相交于点O,∠DOB是它的余角的2倍,∠AOE=2∠DOF,且有OG⊥AB,求∠EOG的度数.
四、综合题
24.如图,已知直线 AB , CD 相交于点 O , ∠AOE 与 ∠AOC 互余.
(1)若 ∠BOD=32° ,求 ∠AOE 的度数;
(2)若 ∠AOD:∠A0C=5:1 ,求 ∠BOE 的度数.
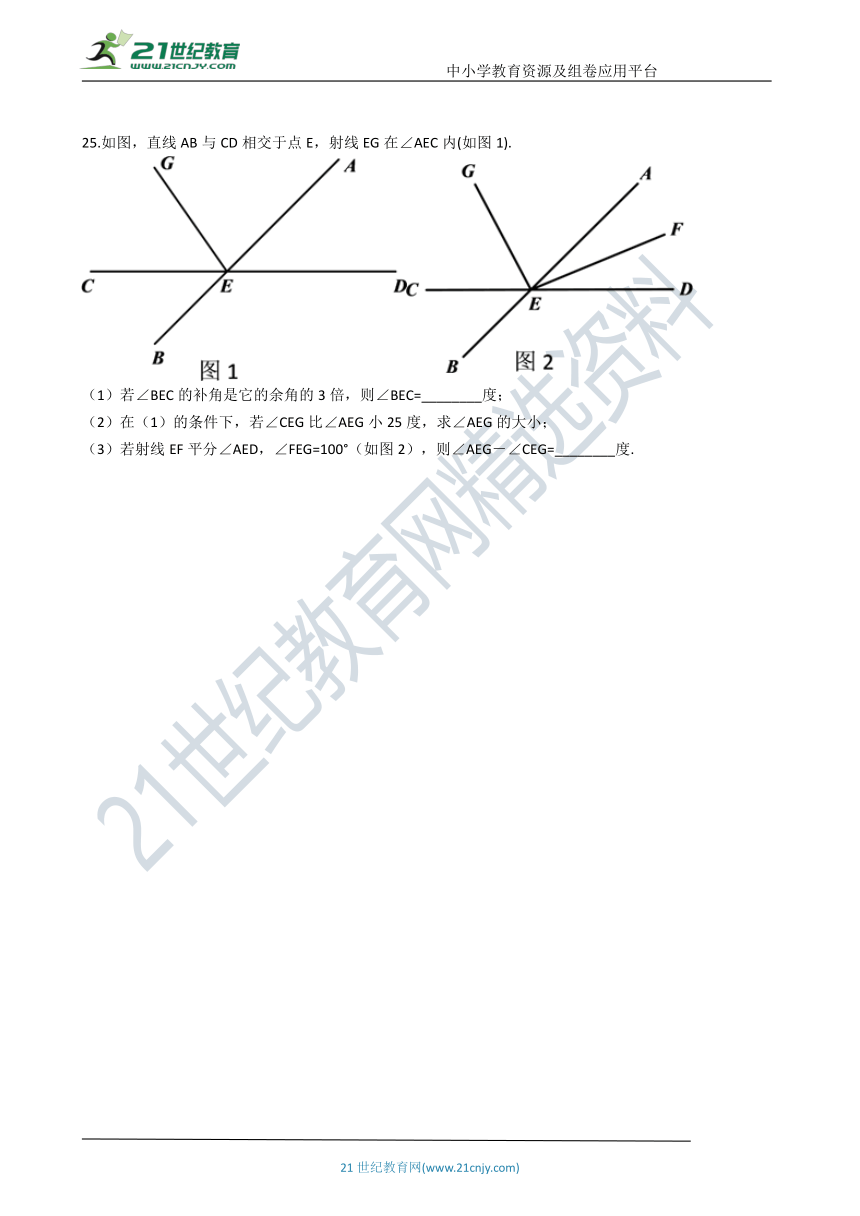
25.如图,直线AB与CD相交于点E,射线EG在∠AEC内(如图1).
(1)若∠BEC的补角是它的余角的3倍,则∠BEC=________度;
(2)在(1)的条件下,若∠CEG比∠AEG小25度,求∠AEG的大小;
(3)若射线EF平分∠AED,∠FEG=100°(如图2),则∠AEG-∠CEG=________度.
答案解析部分
一、单选题
1.【答案】 B
解: “两点之间,线段最短”是一个定理,把弯路改成直路可以缩短路程也是必然的事件,而A、C、D体现是两点确定一条直线的基本事实.
故答案为:B.
2.【答案】 B
解:∵三角板的两个直角都等于90°,即∠BOD+∠AOC=180°,
∵∠BOD+∠AOC=∠AOB+∠COD,
又∵∠AOB=160°,
∴∠COD=20°.
故选:B.
3.【答案】 C
解:观察数轴可知点A与点B之间的距离是5个单位长度,点B在点A的右侧,
因为点A表示的数是-2,-2+5=3,
所以点B表示的数是3,
故答案为:C.
4.【答案】 D
解:如图,∠AOB=60°,∠AOC=15°,
当点C在∠AOB内部时,
∠BOC=∠AOB-∠AOC=45°,
当点C在∠AOB外部时,
∠BOC=∠AOB+∠AOC=75°,
故答案为:D.
5.【答案】 C
解:∵∠ABD=45°,∠CBD=90°,
∴∠ABC=45°+90°=135°,
故答案为:C.
6.【答案】 C
解:∵OE⊥AB,
∴∠AOE=∠BOE=90°,
∴∠DOE+∠BOD=90°,
∵∠BOD=∠AOC,
∴∠DOE+∠AOC=90°,
即∠DOE与∠COA互余.
故答案为:C.
7.【答案】 A
解: OA 方向是北偏东 70° ,故A选项错误;
OB 方向是北偏西15°,故B选项正确;
OC 方向是南偏西30°,故C选项正确;
OD 方向是东南方向,故D选项正确.
故答案为:A.
8.【答案】 B
解:A、∠1和∠2不是对顶角,故错误;
B、∠1和∠2是对顶角,故正确;
C、∠1和∠2不是对顶角,故错误;
D、∠1和∠2不是对顶角,故错误.
故答案为:B.
9.【答案】 D
解:现实生活中“为何有人乱穿马路,却不愿从天桥或斑马线通过?”,
其原因是两点之间,线段最短,
故答案为:D.
10.【答案】 B
解:图中,∠2=∠COE(对顶角相等),
又∵AB⊥CD,
∴∠1+∠COE=90°,
∴∠1+∠2=90°,
∴两角互余.
故答案为:B.
二、填空题
11.【答案】 21°18′
解: ∵ ∠α=68°42'
∴ ∠α 的余角为 90°?68°42′=89°60′?68°42′=21°18′
故答案为:21°18′.
12.【答案】 146°
解: ∵∠A=34°
∴ ∠A 的补角为: 180°?34°=146°
故答案为: 146° .
13.【答案】 70°
解:分针每分钟转动:360÷60=6度,
时针每分钟转动:360÷12÷60=0.5度,
180°?20×6°+0.5°×20=70° .
故答案为:70°.
14.【答案】 75
解:如图,
∵ ∠2=135°?60°=75° ,
∴ ∠1=∠2=75° .
故答案为:75.
15.【答案】 58
解:∵∠BAC= 60° , ∠1=28° ,
∴∠EAC=∠BAC-∠1= 60°?28°=32° ,
∵∠DAE= 90° ,
∴∠2=∠DAE-∠EAC= 90°?32°=58° ,
故答案为:58 .
16.【答案】 60°
解:有图意可得:∵90°-30°=60°,
∴射线OA表示为南偏东60°.
故答案为:60°.
17.【答案】 两点之间,线段最短
解:这个基本事实是:两点之间,线段最短.
故答案为:两点之间,线段最短.
18.【答案】 ②④
解:①用两个钉子就可以把木条固定在墙上,可用两点可确定一条直线解释;
②把弯曲的公路改直,就能缩短路程,可用两点之间,线段最短解释;
③植树时,只要确定两棵树的位置,就能确定同一行树所在的直线,可用两点可确定一条直线解释;
④从 A 地到 B 地架设电线,总是尽可能沿着线段 AB 架设,可用两点之间,线段最短解释;
故答案为:②④.
19.【答案】 50°
【考点】角的运算,对顶角及其性质
解:∵OE⊥CD,
∴∠EOD=90°,
∵∠BOE=40°,
∴∠BOD=90°?40°=50°,
∴∠AOC=∠BOD=50°.
故答案是:50°.
20.【答案】 4
解:由题意可得:
|x+3|+|x?1| 表示x与-3的距离和x与1的距离之和,
|y+2|+|y?3| 表示y与-2的距离和y与3的距离之和,
∴当-3≤x≤1时, |x+3|+|x?1| 有最小值,且为1-(-3)=4,
当-2≤x≤3时, |y+2|+|y?3| 有最小值,且为3-(-2)=5,
∵ |x+3|+|x?1|+|y+2|+|y?3|=9 ,
∴ |x+3|+|x?1| =4, |y+2|+|y?3| =5,
∴x+y的最大值为:1+3=4,
故答案为:4.
三、解答题
21.【答案】 解:设这个角的度数为x,根据题意得:
90°﹣x= 12 (180°﹣x)﹣15°
解得:x=30°.
答:这个角的度数为30°.
22.【答案】 解:∵ CO⊥AB ,
∴ ∠AOC=∠BOC=90? ,
∴ ∠BOD+∠COD=90? ,
∵ ∠BOD?∠COD=34? ,
∴ ∠COD=28? ,
∴ ∠AOD=∠AOC+∠COD=118? .
23.【答案】 解:设∠DOB=x,则其余角为: 12 x,∴x+ 12 x=90°,解得:x=60°,
根据∠AOE=2∠DOF,∵∠AOE=∠BOF(对顶角相等),∴3∠DOF=∠DOB=60°,
故∠DOF=20°,∠BOF=40°,
∵有OG⊥OA,
∴∠EOG=90°-∠BOF=50°.
故∠EOG的度数是50°.
四、综合题
24.【答案】 (1)解:因为 ∠AOC 与 ∠BOD 是对顶角,
所以 ∠AOC=∠BOD=32° ,
因为 ∠AOE 与 ∠AOC 互余,
所以 ∠AOE+∠AOC=90° ,
所以 ∠AOE=90°?∠AOC
=90°?32°
=58° ;
(2)解:因为 ∠AOD:∠AOC=5:1 ,
所以 ∠AOD=5∠AOC ,
因为 ∠AOC+∠AOD=180° ,
所以 6∠AOC=180° ,
∠AOC=30° ,
又 ∠BOD=∠AOC=30° ,
∠COE=∠DOE=90° ,
所以 ∠BOE=∠DOE+∠BOD
=90°+30°
=120° .
25.【答案】 (1)45°
(2)解: ∵∠BEC=45? ,
∴∠AEC=135? ,
设 ∠AEG=x, 则 ∠CEG=x?25? ,
∴x+x?25?=135?
解出: x=80? .
∴∠AEG=80? .
(3)20.
解:(1)根据题意得:
设 ∠BEC=x ,则它的余角为 90??x ,它的补角为 180??x ,
即: 180??x=3×(90??x)
解得: x=45? ,
∴∠BEC=45? .
( 3 )根据射线 EF 平分 ∠AED ,设 ∠AEF=∠FED=x ,则 ∠AEG=100??x ,
∴ ∠CEG=180??∠GED=180??(100?+x)=80??x ,
∠AEG=∠FEG?∠AEF=100??x ,
∴∠AEG?∠CEG=20? ,
故答案为: 20? .
一、单选题
1.在下列日常生活的操作中,能体现基本事实“两点之间,线段最短”的是(?????? )
A.?用两颗钉子可以固定一根木条 B.?把弯路改直可以缩短路程
C.?用两根木桩拉一直线可把树栽成一排 D.?沿桌子的一边看,可将桌子排整齐
2.如图是一副三角板摆成的图形,如果 ∠AOB=160° ,那么 ∠COD 等于(?? )
A.?15°???????????????????????????????????????B.?20°???????????????????????????????????????C.?30°???????????????????????????????????????D.?40°
3.如图,数轴的单位长度为1,如果点 A 表示的数为-2,那么点 B 表示的数是(?? ).
A.?-1???????????????????????????????????????????B.?0???????????????????????????????????????????C.?3???????????????????????????????????????????D.?4
4.如图, ∠AOB=60° ,以 OA 为一边作 ∠AOC=15° ,则 ∠BOC 的度数为(?? )
A.?15°???????????????????????????B.?45°???????????????????????????C.?15° 或 75°???????????????????????????D.?45° 或 75°
5.将一副直角三角尺按如图所示摆放,则图中 ∠ABC 的度数是(?? )
A.?105°????????????????????????????????????B.?120°????????????????????????????????????C.?135°????????????????????????????????????D.?150°
6.如图,直线AB和CD相交于O,那么图中 ∠DOE与∠COA? 的关系是(?? )
A.?对顶角????????????????????????????????????B.?相等????????????????????????????????????C.?互余????????????????????????????????????D.?互补
7.如图,下列说法中错误的是(?? ).
A.?OA 方向是北偏东20° B.?OB 方向是北偏西15°
C.?OC 方向是南偏西30° D.?OD 方向是东南方向
8.在下图中,∠1和∠2是对顶角的是(?? )
A.??????????????B.? ??C.??????????????D.?
9.现实生活中“为何有人宁可违反交通规则翻越隔离带乱穿马路,也不愿从天桥或斑马线通过?”,请用数学知识解释这一现象,其原因为( ??)
A.?两点之间线段的长度,叫做这两点之间的距离????B.?过一点有无数条直线
C.?两点确定一条直线??????????????????????????????????????????????D.?两点之间,线段最短
10.已知:如图,AB⊥CD,垂足为O,EF为过点O的一条直线,则∠1与∠2的关系一定成立的是(?? ?)
A.?相等????????????????????????????????????B.?互余????????????????????????????????????C.?互补????????????????????????????????????D.?不确定
二、填空题
11.已知 ∠α=68°42' .则 ∠α 的余角为________.
12.若 ∠A=34° ,则 ∠A 的补角等于________.
13.钟表上显示6时20分,则此刻时针与分针的夹角的度数为________.
14.如图,直线 a 、 b 相交于点 O ,将量角器的中心与点 O 重合,发现表示 60° 的点在直线 a 上,表示 135° 的点在直线 b 上,则 ∠1= ________ ° .
15.如图,将一个三角板 60° 角的顶点与另一个三角板的直角顶点重合, ∠1=28° , ∠2=________° .
16.如图,∠1=30°,则射线OA表示的方位是南偏东________.
17.从甲地到乙地有3条路,但小明说这三条路都不是最短的,小明的依据是________.
18.下列生产和生活现象:①用两个钉子就可以把木条固定在墙上;②把弯曲的公路改直,就能缩短路程;③植树时,只要确定两棵树的位置,就能确定同一行树所在的直线;④从 A 地到 B 地架设电线,总是尽可能沿着线段 AB 架设.其中能用“两点之间,线段最短”来解释的现象有________.(填序号)
19.如图,直线 AB , CD 相交于点 O , OE⊥CD ,垂足为点 O ,若 ∠BOE=40° ,则 ∠AOC 的度数为________.
20.“数形结合”思想在数轴上得到充分体现,如在数轴上表示数5和 ?2 的两点之间的距离,可列式表示为 |5?(?2)| ,或 |?2?5| ;表示数 x 和 ?3 的两点之间的距离可列式表示为 |x?(?3)|=|x+3| .已知 |x+3|+|x?1|+|y+2|+|y?3|=9 ,则 x+y 的最大值为________.
三、解答题
21.一个角的余角比它的补角的 12 还少15°,求这个角的度数.
22.如图,点 O 在直线 AB 上, CO⊥AB , ∠BOD?∠COD=34? ,求 ∠AOD 的度数.
23.如图,直线AB、CD、EF相交于点O,∠DOB是它的余角的2倍,∠AOE=2∠DOF,且有OG⊥AB,求∠EOG的度数.
四、综合题
24.如图,已知直线 AB , CD 相交于点 O , ∠AOE 与 ∠AOC 互余.
(1)若 ∠BOD=32° ,求 ∠AOE 的度数;
(2)若 ∠AOD:∠A0C=5:1 ,求 ∠BOE 的度数.
25.如图,直线AB与CD相交于点E,射线EG在∠AEC内(如图1).
(1)若∠BEC的补角是它的余角的3倍,则∠BEC=________度;
(2)在(1)的条件下,若∠CEG比∠AEG小25度,求∠AEG的大小;
(3)若射线EF平分∠AED,∠FEG=100°(如图2),则∠AEG-∠CEG=________度.
答案解析部分
一、单选题
1.【答案】 B
解: “两点之间,线段最短”是一个定理,把弯路改成直路可以缩短路程也是必然的事件,而A、C、D体现是两点确定一条直线的基本事实.
故答案为:B.
2.【答案】 B
解:∵三角板的两个直角都等于90°,即∠BOD+∠AOC=180°,
∵∠BOD+∠AOC=∠AOB+∠COD,
又∵∠AOB=160°,
∴∠COD=20°.
故选:B.
3.【答案】 C
解:观察数轴可知点A与点B之间的距离是5个单位长度,点B在点A的右侧,
因为点A表示的数是-2,-2+5=3,
所以点B表示的数是3,
故答案为:C.
4.【答案】 D
解:如图,∠AOB=60°,∠AOC=15°,
当点C在∠AOB内部时,
∠BOC=∠AOB-∠AOC=45°,
当点C在∠AOB外部时,
∠BOC=∠AOB+∠AOC=75°,
故答案为:D.
5.【答案】 C
解:∵∠ABD=45°,∠CBD=90°,
∴∠ABC=45°+90°=135°,
故答案为:C.
6.【答案】 C
解:∵OE⊥AB,
∴∠AOE=∠BOE=90°,
∴∠DOE+∠BOD=90°,
∵∠BOD=∠AOC,
∴∠DOE+∠AOC=90°,
即∠DOE与∠COA互余.
故答案为:C.
7.【答案】 A
解: OA 方向是北偏东 70° ,故A选项错误;
OB 方向是北偏西15°,故B选项正确;
OC 方向是南偏西30°,故C选项正确;
OD 方向是东南方向,故D选项正确.
故答案为:A.
8.【答案】 B
解:A、∠1和∠2不是对顶角,故错误;
B、∠1和∠2是对顶角,故正确;
C、∠1和∠2不是对顶角,故错误;
D、∠1和∠2不是对顶角,故错误.
故答案为:B.
9.【答案】 D
解:现实生活中“为何有人乱穿马路,却不愿从天桥或斑马线通过?”,
其原因是两点之间,线段最短,
故答案为:D.
10.【答案】 B
解:图中,∠2=∠COE(对顶角相等),
又∵AB⊥CD,
∴∠1+∠COE=90°,
∴∠1+∠2=90°,
∴两角互余.
故答案为:B.
二、填空题
11.【答案】 21°18′
解: ∵ ∠α=68°42'
∴ ∠α 的余角为 90°?68°42′=89°60′?68°42′=21°18′
故答案为:21°18′.
12.【答案】 146°
解: ∵∠A=34°
∴ ∠A 的补角为: 180°?34°=146°
故答案为: 146° .
13.【答案】 70°
解:分针每分钟转动:360÷60=6度,
时针每分钟转动:360÷12÷60=0.5度,
180°?20×6°+0.5°×20=70° .
故答案为:70°.
14.【答案】 75
解:如图,
∵ ∠2=135°?60°=75° ,
∴ ∠1=∠2=75° .
故答案为:75.
15.【答案】 58
解:∵∠BAC= 60° , ∠1=28° ,
∴∠EAC=∠BAC-∠1= 60°?28°=32° ,
∵∠DAE= 90° ,
∴∠2=∠DAE-∠EAC= 90°?32°=58° ,
故答案为:58 .
16.【答案】 60°
解:有图意可得:∵90°-30°=60°,
∴射线OA表示为南偏东60°.
故答案为:60°.
17.【答案】 两点之间,线段最短
解:这个基本事实是:两点之间,线段最短.
故答案为:两点之间,线段最短.
18.【答案】 ②④
解:①用两个钉子就可以把木条固定在墙上,可用两点可确定一条直线解释;
②把弯曲的公路改直,就能缩短路程,可用两点之间,线段最短解释;
③植树时,只要确定两棵树的位置,就能确定同一行树所在的直线,可用两点可确定一条直线解释;
④从 A 地到 B 地架设电线,总是尽可能沿着线段 AB 架设,可用两点之间,线段最短解释;
故答案为:②④.
19.【答案】 50°
【考点】角的运算,对顶角及其性质
解:∵OE⊥CD,
∴∠EOD=90°,
∵∠BOE=40°,
∴∠BOD=90°?40°=50°,
∴∠AOC=∠BOD=50°.
故答案是:50°.
20.【答案】 4
解:由题意可得:
|x+3|+|x?1| 表示x与-3的距离和x与1的距离之和,
|y+2|+|y?3| 表示y与-2的距离和y与3的距离之和,
∴当-3≤x≤1时, |x+3|+|x?1| 有最小值,且为1-(-3)=4,
当-2≤x≤3时, |y+2|+|y?3| 有最小值,且为3-(-2)=5,
∵ |x+3|+|x?1|+|y+2|+|y?3|=9 ,
∴ |x+3|+|x?1| =4, |y+2|+|y?3| =5,
∴x+y的最大值为:1+3=4,
故答案为:4.
三、解答题
21.【答案】 解:设这个角的度数为x,根据题意得:
90°﹣x= 12 (180°﹣x)﹣15°
解得:x=30°.
答:这个角的度数为30°.
22.【答案】 解:∵ CO⊥AB ,
∴ ∠AOC=∠BOC=90? ,
∴ ∠BOD+∠COD=90? ,
∵ ∠BOD?∠COD=34? ,
∴ ∠COD=28? ,
∴ ∠AOD=∠AOC+∠COD=118? .
23.【答案】 解:设∠DOB=x,则其余角为: 12 x,∴x+ 12 x=90°,解得:x=60°,
根据∠AOE=2∠DOF,∵∠AOE=∠BOF(对顶角相等),∴3∠DOF=∠DOB=60°,
故∠DOF=20°,∠BOF=40°,
∵有OG⊥OA,
∴∠EOG=90°-∠BOF=50°.
故∠EOG的度数是50°.
四、综合题
24.【答案】 (1)解:因为 ∠AOC 与 ∠BOD 是对顶角,
所以 ∠AOC=∠BOD=32° ,
因为 ∠AOE 与 ∠AOC 互余,
所以 ∠AOE+∠AOC=90° ,
所以 ∠AOE=90°?∠AOC
=90°?32°
=58° ;
(2)解:因为 ∠AOD:∠AOC=5:1 ,
所以 ∠AOD=5∠AOC ,
因为 ∠AOC+∠AOD=180° ,
所以 6∠AOC=180° ,
∠AOC=30° ,
又 ∠BOD=∠AOC=30° ,
∠COE=∠DOE=90° ,
所以 ∠BOE=∠DOE+∠BOD
=90°+30°
=120° .
25.【答案】 (1)45°
(2)解: ∵∠BEC=45? ,
∴∠AEC=135? ,
设 ∠AEG=x, 则 ∠CEG=x?25? ,
∴x+x?25?=135?
解出: x=80? .
∴∠AEG=80? .
(3)20.
解:(1)根据题意得:
设 ∠BEC=x ,则它的余角为 90??x ,它的补角为 180??x ,
即: 180??x=3×(90??x)
解得: x=45? ,
∴∠BEC=45? .
( 3 )根据射线 EF 平分 ∠AED ,设 ∠AEF=∠FED=x ,则 ∠AEG=100??x ,
∴ ∠CEG=180??∠GED=180??(100?+x)=80??x ,
∠AEG=∠FEG?∠AEF=100??x ,
∴∠AEG?∠CEG=20? ,
故答案为: 20? .
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
