北京市12中2020-2021学年高一下学期期中考试数学试题 Word版含答案
文档属性
| 名称 | 北京市12中2020-2021学年高一下学期期中考试数学试题 Word版含答案 |

|
|
| 格式 | doc | ||
| 文件大小 | 820.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-31 20:24:20 | ||
图片预览



文档简介
北京市12中2020-2021学年第二学期高一年级期中考试
数学 2021.05
本试卷共4页,满分150分.考试时长120分钟.考生务必将答案答在答题纸上,在试巻上作答无效.考试结束后,将答题纸交回.
第一部分 选择题(共60分)
一、选择题共12小题,每小题5分,共60分,在每小题列出的四个选项中,选出符合题目要求的一项
1. 若复数,则复数所对应的点在
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
2. 已知向量,若,则( )
A. B. 11 C. -10 D. 10
3. 已知是表示平面内所有向量的一组基底,则下列四个向量中,不能作为一组基底的是( )
A. B.
C. D.
4. 某几何体有6个顶点,则该几何体不可能是( )
A. 五棱锥 B. 三棱柱 C. 三棱台 D. 四棱台
5. 已知,且为锐角,则( )
A. B. C. D.
6. 对于任意向量,下列命题中正确是( )
A. 若,则 B.
C. D.
7. 记知向量,且,则( )
A. 3 B. -3 C. D. -
8. 在中,角对边分別,且,则( )
A. 60°或120° B. 60° C. 30° D. 30°或150°
9. 在△ABC中,已知,则△ABC一定是( )
A. 锐角三角形 B. 钝角三角形
C. 直角三角形 D. 等腰直角三角形
10. 设,则有( )
A. B. C. D.
11. 已知中,,,,为所在平面内一点,且,则值为( )
A.
B.
C.
D.
12. 我国古代数学家秦九韶左《数书九章》中记述了了“一斜求积术”,用现代式子表示即为:在中,角A,B,C所对的边分别为a,b,c,则的面积,根据此公式,若,且,则的面积为( )
A. B.
C. D.
第二部分 非选择题(共90分)
二、填空题共6小题,每小题5分,共30分.
13. ___________.
14. ________.
15. 已知为单位向量,,则的夹角为________.
16. 若实数满足方程组,则一个值是________.(答案不唯一,写出满足条件的一个值即可)
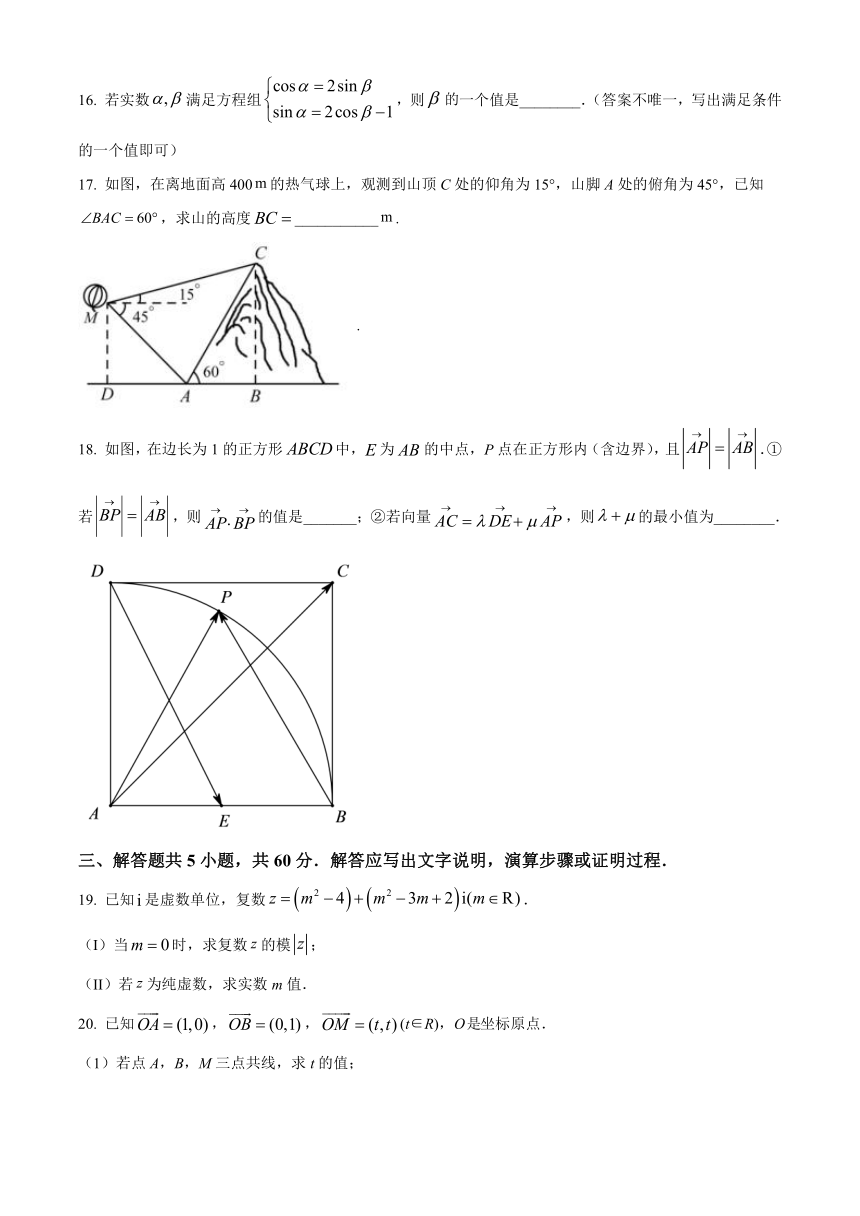
17. 如图,在离地面高400的热气球上,观测到山顶C处的仰角为15°,山脚A处的俯角为45°,已知,求山的高度___________.
.
18. 如图,在边长为1的正方形中,为的中点,点在正方形内(含边界),且.①若,则的值是_______;②若向量,则的最小值为________.
三、解答题共5小题,共60分.解答应写出文字说明,演算步骤或证明过程.
19. 已知是虚数单位,复数.
(I)当时,求复数的模;
(II)若为纯虚数,求实数m值.
20. 已知,,(t∈R),O坐标原点.
(1)若点A,B,M三点共线,求t的值;
(2)当t取何值时,取到最小值?并求出最小值.
21. 已知函数.
(I)求的值;
(II)求的最小正周期和对称轴方程;
(III)求在上的值域.
22. 锐角中满足,其中分別为内角的对边.
(I)求角;
(II)若,求的取值范围.
23. 定义向量的“相伴函数”为,函数的“相伴向量”为,其中O为坐标原点,记平面内所有向量的“相伴函数”构成的集合为S.
(I)设函数,求证:;
(II)记向量的相伴函数为,当且时,求的值;
(III)将(I)中函数的图像向右平移个单位长度,再把横坐标伸长为原来的2倍(纵坐标不变)得到的图像.已知,问在的图像上是否存在一点,使得.若存在,求出点坐标;若不存在,说明理由.
北京市12中2020-2021学年第二学期高一年级期中考试
数学 2021.05 答案版
本试卷共4页,满分150分.考试时长120分钟.考生务必将答案答在答题纸上,在试巻上作答无效.考试结束后,将答题纸交回.
第一部分 选择题(共60分)
一、选择题共12小题,每小题5分,共60分,在每小题列出的四个选项中,选出符合题目要求的一项
1. 若复数,则复数所对应的点在
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
【答案】A
2. 已知向量,若,则( )
A. B. 11 C. -10 D. 10
【答案】D
3. 已知是表示平面内所有向量的一组基底,则下列四个向量中,不能作为一组基底的是( )
A. B.
C. D.
【答案】B
4. 某几何体有6个顶点,则该几何体不可能是( )
A. 五棱锥 B. 三棱柱 C. 三棱台 D. 四棱台
【答案】D
5. 已知,且为锐角,则( )
A. B. C. D.
【答案】C
6. 对于任意向量,下列命题中正确是( )
A. 若,则 B.
C. D.
【答案】B
7. 记知向量,且,则( )
A. 3 B. -3 C. D. -
【答案】C
8. 在中,角对边分別,且,则( )
A. 60°或120° B. 60° C. 30° D. 30°或150°
【答案】A
9. 在△ABC中,已知,则△ABC一定是( )
A. 锐角三角形 B. 钝角三角形
C. 直角三角形 D. 等腰直角三角形
【答案】C
10. 设,则有( )
A. B. C. D.
【答案】C
11. 已知中,,,,为所在平面内一点,且,则值为( )
A.
B.
C.
D.
【答案】B
12. 我国古代数学家秦九韶左《数书九章》中记述了了“一斜求积术”,用现代式子表示即为:在中,角A,B,C所对的边分别为a,b,c,则的面积,根据此公式,若,且,则的面积为( )
A. B.
C. D.
【答案】B
第二部分 非选择题(共90分)
二、填空题共6小题,每小题5分,共30分.
13. ___________.
【答案】
14. ________.
【答案】
15. 已知为单位向量,,则的夹角为________.
【答案】
16. 若实数满足方程组,则一个值是________.(答案不唯一,写出满足条件的一个值即可)
【答案】
17. 如图,在离地面高400的热气球上,观测到山顶C处的仰角为15°,山脚A处的俯角为45°,已知,求山的高度___________.
.
【答案】
18. 如图,在边长为1的正方形中,为的中点,点在正方形内(含边界),且.①若,则的值是_______;②若向量,则的最小值为________.
【答案】 ①. ②.
三、解答题共5小题,共60分.解答应写出文字说明,演算步骤或证明过程.
19. 已知是虚数单位,复数.
(I)当时,求复数的模;
(II)若为纯虚数,求实数m值.
【答案】(I);(II)
20. 已知,,(t∈R),O坐标原点.
(1)若点A,B,M三点共线,求t的值;
(2)当t取何值时,取到最小值?并求出最小值.
【答案】(1)t;(2)当t时,?的最小值为.
21. 已知函数.
(I)求的值;
(II)求的最小正周期和对称轴方程;
(III)求在上的值域.
【答案】(I);(II),;(III)
22. 锐角中满足,其中分別为内角的对边.
(I)求角;
(II)若,求的取值范围.
【答案】(I);(II)
23. 定义向量的“相伴函数”为,函数的“相伴向量”为,其中O为坐标原点,记平面内所有向量的“相伴函数”构成的集合为S.
(I)设函数,求证:;
(II)记向量的相伴函数为,当且时,求的值;
(III)将(I)中函数的图像向右平移个单位长度,再把横坐标伸长为原来的2倍(纵坐标不变)得到的图像.已知,问在的图像上是否存在一点,使得.若存在,求出点坐标;若不存在,说明理由.
【答案】(I)证明见解析;(II);(III)存在,.
数学 2021.05
本试卷共4页,满分150分.考试时长120分钟.考生务必将答案答在答题纸上,在试巻上作答无效.考试结束后,将答题纸交回.
第一部分 选择题(共60分)
一、选择题共12小题,每小题5分,共60分,在每小题列出的四个选项中,选出符合题目要求的一项
1. 若复数,则复数所对应的点在
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
2. 已知向量,若,则( )
A. B. 11 C. -10 D. 10
3. 已知是表示平面内所有向量的一组基底,则下列四个向量中,不能作为一组基底的是( )
A. B.
C. D.
4. 某几何体有6个顶点,则该几何体不可能是( )
A. 五棱锥 B. 三棱柱 C. 三棱台 D. 四棱台
5. 已知,且为锐角,则( )
A. B. C. D.
6. 对于任意向量,下列命题中正确是( )
A. 若,则 B.
C. D.
7. 记知向量,且,则( )
A. 3 B. -3 C. D. -
8. 在中,角对边分別,且,则( )
A. 60°或120° B. 60° C. 30° D. 30°或150°
9. 在△ABC中,已知,则△ABC一定是( )
A. 锐角三角形 B. 钝角三角形
C. 直角三角形 D. 等腰直角三角形
10. 设,则有( )
A. B. C. D.
11. 已知中,,,,为所在平面内一点,且,则值为( )
A.
B.
C.
D.
12. 我国古代数学家秦九韶左《数书九章》中记述了了“一斜求积术”,用现代式子表示即为:在中,角A,B,C所对的边分别为a,b,c,则的面积,根据此公式,若,且,则的面积为( )
A. B.
C. D.
第二部分 非选择题(共90分)
二、填空题共6小题,每小题5分,共30分.
13. ___________.
14. ________.
15. 已知为单位向量,,则的夹角为________.
16. 若实数满足方程组,则一个值是________.(答案不唯一,写出满足条件的一个值即可)
17. 如图,在离地面高400的热气球上,观测到山顶C处的仰角为15°,山脚A处的俯角为45°,已知,求山的高度___________.
.
18. 如图,在边长为1的正方形中,为的中点,点在正方形内(含边界),且.①若,则的值是_______;②若向量,则的最小值为________.
三、解答题共5小题,共60分.解答应写出文字说明,演算步骤或证明过程.
19. 已知是虚数单位,复数.
(I)当时,求复数的模;
(II)若为纯虚数,求实数m值.
20. 已知,,(t∈R),O坐标原点.
(1)若点A,B,M三点共线,求t的值;
(2)当t取何值时,取到最小值?并求出最小值.
21. 已知函数.
(I)求的值;
(II)求的最小正周期和对称轴方程;
(III)求在上的值域.
22. 锐角中满足,其中分別为内角的对边.
(I)求角;
(II)若,求的取值范围.
23. 定义向量的“相伴函数”为,函数的“相伴向量”为,其中O为坐标原点,记平面内所有向量的“相伴函数”构成的集合为S.
(I)设函数,求证:;
(II)记向量的相伴函数为,当且时,求的值;
(III)将(I)中函数的图像向右平移个单位长度,再把横坐标伸长为原来的2倍(纵坐标不变)得到的图像.已知,问在的图像上是否存在一点,使得.若存在,求出点坐标;若不存在,说明理由.
北京市12中2020-2021学年第二学期高一年级期中考试
数学 2021.05 答案版
本试卷共4页,满分150分.考试时长120分钟.考生务必将答案答在答题纸上,在试巻上作答无效.考试结束后,将答题纸交回.
第一部分 选择题(共60分)
一、选择题共12小题,每小题5分,共60分,在每小题列出的四个选项中,选出符合题目要求的一项
1. 若复数,则复数所对应的点在
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
【答案】A
2. 已知向量,若,则( )
A. B. 11 C. -10 D. 10
【答案】D
3. 已知是表示平面内所有向量的一组基底,则下列四个向量中,不能作为一组基底的是( )
A. B.
C. D.
【答案】B
4. 某几何体有6个顶点,则该几何体不可能是( )
A. 五棱锥 B. 三棱柱 C. 三棱台 D. 四棱台
【答案】D
5. 已知,且为锐角,则( )
A. B. C. D.
【答案】C
6. 对于任意向量,下列命题中正确是( )
A. 若,则 B.
C. D.
【答案】B
7. 记知向量,且,则( )
A. 3 B. -3 C. D. -
【答案】C
8. 在中,角对边分別,且,则( )
A. 60°或120° B. 60° C. 30° D. 30°或150°
【答案】A
9. 在△ABC中,已知,则△ABC一定是( )
A. 锐角三角形 B. 钝角三角形
C. 直角三角形 D. 等腰直角三角形
【答案】C
10. 设,则有( )
A. B. C. D.
【答案】C
11. 已知中,,,,为所在平面内一点,且,则值为( )
A.
B.
C.
D.
【答案】B
12. 我国古代数学家秦九韶左《数书九章》中记述了了“一斜求积术”,用现代式子表示即为:在中,角A,B,C所对的边分别为a,b,c,则的面积,根据此公式,若,且,则的面积为( )
A. B.
C. D.
【答案】B
第二部分 非选择题(共90分)
二、填空题共6小题,每小题5分,共30分.
13. ___________.
【答案】
14. ________.
【答案】
15. 已知为单位向量,,则的夹角为________.
【答案】
16. 若实数满足方程组,则一个值是________.(答案不唯一,写出满足条件的一个值即可)
【答案】
17. 如图,在离地面高400的热气球上,观测到山顶C处的仰角为15°,山脚A处的俯角为45°,已知,求山的高度___________.
.
【答案】
18. 如图,在边长为1的正方形中,为的中点,点在正方形内(含边界),且.①若,则的值是_______;②若向量,则的最小值为________.
【答案】 ①. ②.
三、解答题共5小题,共60分.解答应写出文字说明,演算步骤或证明过程.
19. 已知是虚数单位,复数.
(I)当时,求复数的模;
(II)若为纯虚数,求实数m值.
【答案】(I);(II)
20. 已知,,(t∈R),O坐标原点.
(1)若点A,B,M三点共线,求t的值;
(2)当t取何值时,取到最小值?并求出最小值.
【答案】(1)t;(2)当t时,?的最小值为.
21. 已知函数.
(I)求的值;
(II)求的最小正周期和对称轴方程;
(III)求在上的值域.
【答案】(I);(II),;(III)
22. 锐角中满足,其中分別为内角的对边.
(I)求角;
(II)若,求的取值范围.
【答案】(I);(II)
23. 定义向量的“相伴函数”为,函数的“相伴向量”为,其中O为坐标原点,记平面内所有向量的“相伴函数”构成的集合为S.
(I)设函数,求证:;
(II)记向量的相伴函数为,当且时,求的值;
(III)将(I)中函数的图像向右平移个单位长度,再把横坐标伸长为原来的2倍(纵坐标不变)得到的图像.已知,问在的图像上是否存在一点,使得.若存在,求出点坐标;若不存在,说明理由.
【答案】(I)证明见解析;(II);(III)存在,.
同课章节目录
