福建省福州格致2020-2021学年高一下学期期中考试数学试题 Word版含答案
文档属性
| 名称 | 福建省福州格致2020-2021学年高一下学期期中考试数学试题 Word版含答案 | 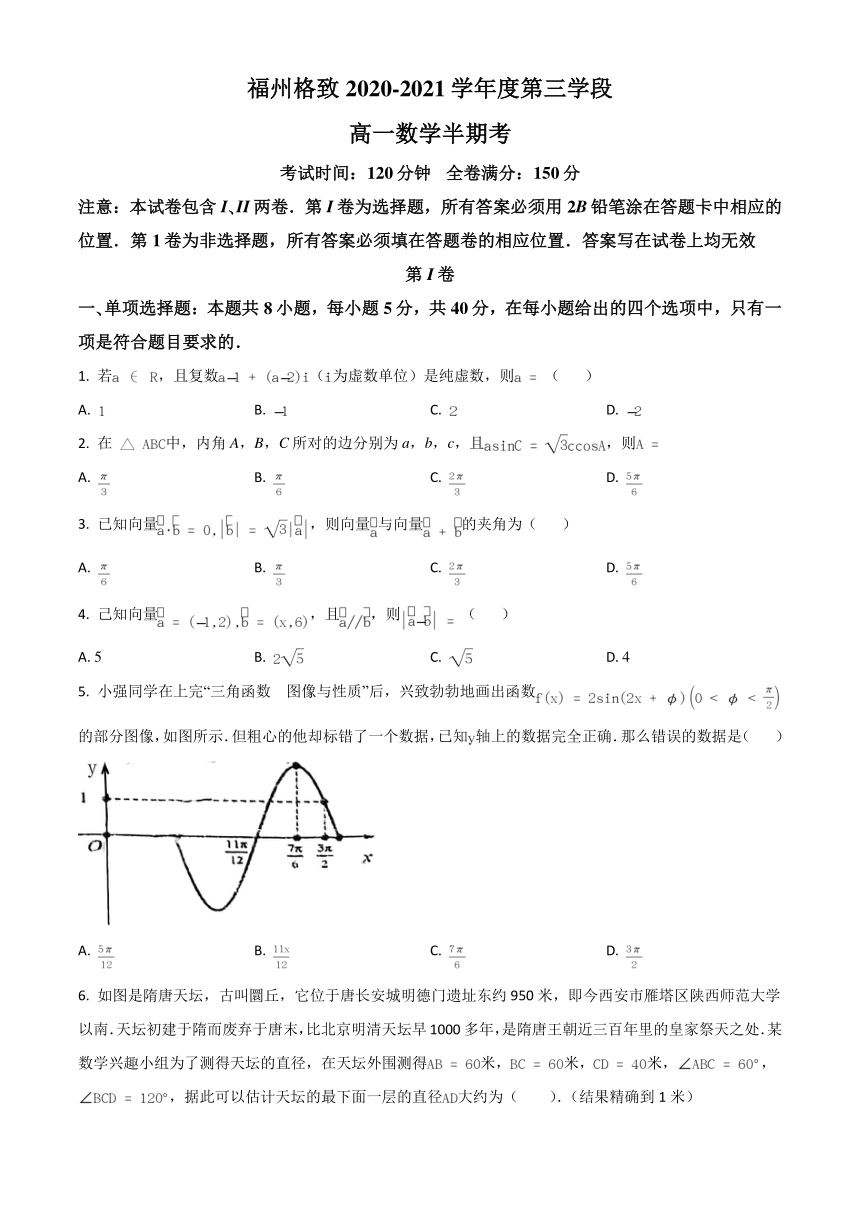 | |
| 格式 | doc | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-31 20:26:14 | ||
图片预览




文档简介
福州格致2020-2021学年度第三学段
高一数学半期考
考试时间:120分钟 全卷满分:150分
注意:本试卷包含I?II两卷.第I卷为选择题,所有答案必须用2B铅笔涂在答题卡中相应的位置.第1卷为非选择题,所有答案必须填在答题卷的相应位置.答案写在试卷上均无效
第I卷
一?单项选择题:本题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 若,且复数(为虚数单位)是纯虚数,则( )
A. B. C. D.
2. 在中,内角A,B,C所对的边分别为a,b,c,且,则
A. B. C. D.
3. 已知向量,则向量与向量的夹角为( )
A. B. C. D.
4. 己知向量,且,则( )
A. 5 B. C. D. 4
5. 小强同学在上完“三角函数图像与性质”后,兴致勃勃地画出函数的部分图像,如图所示.但粗心的他却标错了一个数据,已知轴上的数据完全正确.那么错误的数据是( )
A. B. C. D.
6. 如图是隋唐天坛,古叫圜丘,它位于唐长安城明德门遗址东约950米,即今西安市雁塔区陕西师范大学以南.天坛初建于隋而废弃于唐末,比北京明清天坛早1000多年,是隋唐王朝近三百年里的皇家祭天之处.某数学兴趣小组为了测得天坛的直径,在天坛外围测得米,米,米,,,据此可以估计天坛的最下面一层的直径大约为( ).(结果精确到1米)
(参考数据:,,,)
A. 39米 B. 43米 C. 49米 D. 53米
7. 已知函数,若,则( )
A. 等于 B. 等于 C. 等于 D. 无法确定
8. 中,角所对边分别为,且若,则的最大值是( )
A. B. C. 3 D.
二?多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求,全部选对的得5分,有选错的得0分,部分选对的得3分
9. 已知向量不共线,且,其中,若三点共线,则角的值可以是( )
A. B. C. D.
10. 若△ABC内角A,B,C所对的边分别为a,b,c,且满足b﹣2a+4asin2=0,则下列结论正确的是( )
A. 角C一定为锐角 B. a2+2b2﹣c2=0
C. 3tanA+tanC=0 D. tanB的最小值为
11. 已知函数,若,则下列不等式一定成立的有( )
A. B.
C. D.
12. 已知是所在平面内一点,以下说法正确的是( )
A. 若动点满足,则点的轨迹一定通过的重心.
B. 若点满足,则点是垂心.
C. 若为的外心,且,则是的内心.
D. 若,则点为的外心
三?填空题:本题共4小题,每小题5分,共20分.
13. 在复平面内,若数满足,则的最大值为__________.
14. 中,内角对应的边分别为,若,,则的外接圆面积为__________.
15. 定义在上的奇函数满足,且当时,,则函数在上的零点之和为____________.
16. 中,内角所对的边分别为的平分线交于点,且,若,则的最小值为__________.
四?解答题:本题共6小题,共70分.解答应写出文字说明?证明过程或演算步骤.
17. 中,角所对的边分别为,已知,
(1)求角的大小;
(2)若的面积为,求的周长.
18. 中,角所对的边分别为,已知
(1)试判断的形状;
(2)若的周长为5,且,求.
19. 函数部分图象如图所示.
(Ⅰ)求函数的解析式,并写出其对称中心;
(Ⅱ)若方程有实数解,求的取值范围.
20. 在中,角所对的边分别为,
(1)若,用表示;
(2)已知分别为的中点,若,求证:.
21. 如图,某超市的平面图为矩形ABCD,超市门EF在边AD上,其中
(1)求的正切值:
(2)若要在边上找一点安装安防摄像头,使得对超市门的摄像视角最大,求的长.
22. 已知函数在区间上有最大值4和最小值
(1)求?的值;
(2)设
①若时,,求实数的取值范围;
②若方程有三个不同的实数解,求实数的取值范围.
福州格致2020-2021学年度第三学段
高一数学半期考 答案版
考试时间:120分钟 全卷满分:150分
注意:本试卷包含I?II两卷.第I卷为选择题,所有答案必须用2B铅笔涂在答题卡中相应的位置.第1卷为非选择题,所有答案必须填在答题卷的相应位置.答案写在试卷上均无效
第I卷
一?单项选择题:本题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 若,且复数(为虚数单位)是纯虚数,则( )
A. B. C. D.
【答案】A
2. 在中,内角A,B,C所对的边分别为a,b,c,且,则
A. B. C. D.
【答案】A
3. 已知向量,则向量与向量的夹角为( )
A. B. C. D.
【答案】B
4. 己知向量,且,则( )
A. 5 B. C. D. 4
【答案】B
5. 小强同学在上完“三角函数图像与性质”后,兴致勃勃地画出函数的部分图像,如图所示.但粗心的他却标错了一个数据,已知轴上的数据完全正确.那么错误的数据是( )
A. B. C. D.
【答案】D
6. 如图是隋唐天坛,古叫圜丘,它位于唐长安城明德门遗址东约950米,即今西安市雁塔区陕西师范大学以南.天坛初建于隋而废弃于唐末,比北京明清天坛早1000多年,是隋唐王朝近三百年里的皇家祭天之处.某数学兴趣小组为了测得天坛的直径,在天坛外围测得米,米,米,,,据此可以估计天坛的最下面一层的直径大约为( ).(结果精确到1米)
(参考数据:,,,)
A. 39米 B. 43米 C. 49米 D. 53米
【答案】D
7. 已知函数,若,则( )
A. 等于 B. 等于 C. 等于 D. 无法确定
【答案】C
8. 中,角所对边分别为,且若,则的最大值是( )
A. B. C. 3 D.
【答案】A
二?多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求,全部选对的得5分,有选错的得0分,部分选对的得3分
9. 已知向量不共线,且,其中,若三点共线,则角的值可以是( )
A. B. C. D.
【答案】CD
10. 若△ABC内角A,B,C所对的边分别为a,b,c,且满足b﹣2a+4asin2=0,则下列结论正确的是( )
A. 角C一定为锐角 B. a2+2b2﹣c2=0
C. 3tanA+tanC=0 D. tanB的最小值为
【答案】BC
11. 已知函数,若,则下列不等式一定成立的有( )
A. B.
C. D.
【答案】BD
12. 已知是所在平面内一点,以下说法正确的是( )
A. 若动点满足,则点的轨迹一定通过的重心.
B. 若点满足,则点是垂心.
C. 若为的外心,且,则是的内心.
D. 若,则点为的外心
【答案】AD
三?填空题:本题共4小题,每小题5分,共20分.
13. 在复平面内,若数满足,则的最大值为__________.
【答案】
14. 中,内角对应的边分别为,若,,则的外接圆面积为__________.
【答案】
15. 定义在上的奇函数满足,且当时,,则函数在上的零点之和为____________.
【答案】6
16. 中,内角所对的边分别为的平分线交于点,且,若,则的最小值为__________.
【答案】16
四?解答题:本题共6小题,共70分.解答应写出文字说明?证明过程或演算步骤.
17. 中,角所对的边分别为,已知,
(1)求角的大小;
(2)若的面积为,求的周长.
【答案】(1);(2).
18. 中,角所对的边分别为,已知
(1)试判断的形状;
(2)若的周长为5,且,求.
【答案】(1)等腰三角形;(2)1.
19. 函数部分图象如图所示.
(Ⅰ)求函数的解析式,并写出其对称中心;
(Ⅱ)若方程有实数解,求的取值范围.
【答案】(Ⅰ) 函数的对称中心为(Ⅱ)
20. 在中,角所对的边分别为,
(1)若,用表示;
(2)已知分别为的中点,若,求证:.
【答案】(1);(2)证明见解析
21. 如图,某超市的平面图为矩形ABCD,超市门EF在边AD上,其中
(1)求的正切值:
(2)若要在边上找一点安装安防摄像头,使得对超市门的摄像视角最大,求的长.
【答案】(1);(2)m.
22. 已知函数在区间上有最大值4和最小值
(1)求?的值;
(2)设
①若时,,求实数的取值范围;
②若方程有三个不同的实数解,求实数的取值范围.
【答案】(1);(2)①;② .
高一数学半期考
考试时间:120分钟 全卷满分:150分
注意:本试卷包含I?II两卷.第I卷为选择题,所有答案必须用2B铅笔涂在答题卡中相应的位置.第1卷为非选择题,所有答案必须填在答题卷的相应位置.答案写在试卷上均无效
第I卷
一?单项选择题:本题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 若,且复数(为虚数单位)是纯虚数,则( )
A. B. C. D.
2. 在中,内角A,B,C所对的边分别为a,b,c,且,则
A. B. C. D.
3. 已知向量,则向量与向量的夹角为( )
A. B. C. D.
4. 己知向量,且,则( )
A. 5 B. C. D. 4
5. 小强同学在上完“三角函数图像与性质”后,兴致勃勃地画出函数的部分图像,如图所示.但粗心的他却标错了一个数据,已知轴上的数据完全正确.那么错误的数据是( )
A. B. C. D.
6. 如图是隋唐天坛,古叫圜丘,它位于唐长安城明德门遗址东约950米,即今西安市雁塔区陕西师范大学以南.天坛初建于隋而废弃于唐末,比北京明清天坛早1000多年,是隋唐王朝近三百年里的皇家祭天之处.某数学兴趣小组为了测得天坛的直径,在天坛外围测得米,米,米,,,据此可以估计天坛的最下面一层的直径大约为( ).(结果精确到1米)
(参考数据:,,,)
A. 39米 B. 43米 C. 49米 D. 53米
7. 已知函数,若,则( )
A. 等于 B. 等于 C. 等于 D. 无法确定
8. 中,角所对边分别为,且若,则的最大值是( )
A. B. C. 3 D.
二?多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求,全部选对的得5分,有选错的得0分,部分选对的得3分
9. 已知向量不共线,且,其中,若三点共线,则角的值可以是( )
A. B. C. D.
10. 若△ABC内角A,B,C所对的边分别为a,b,c,且满足b﹣2a+4asin2=0,则下列结论正确的是( )
A. 角C一定为锐角 B. a2+2b2﹣c2=0
C. 3tanA+tanC=0 D. tanB的最小值为
11. 已知函数,若,则下列不等式一定成立的有( )
A. B.
C. D.
12. 已知是所在平面内一点,以下说法正确的是( )
A. 若动点满足,则点的轨迹一定通过的重心.
B. 若点满足,则点是垂心.
C. 若为的外心,且,则是的内心.
D. 若,则点为的外心
三?填空题:本题共4小题,每小题5分,共20分.
13. 在复平面内,若数满足,则的最大值为__________.
14. 中,内角对应的边分别为,若,,则的外接圆面积为__________.
15. 定义在上的奇函数满足,且当时,,则函数在上的零点之和为____________.
16. 中,内角所对的边分别为的平分线交于点,且,若,则的最小值为__________.
四?解答题:本题共6小题,共70分.解答应写出文字说明?证明过程或演算步骤.
17. 中,角所对的边分别为,已知,
(1)求角的大小;
(2)若的面积为,求的周长.
18. 中,角所对的边分别为,已知
(1)试判断的形状;
(2)若的周长为5,且,求.
19. 函数部分图象如图所示.
(Ⅰ)求函数的解析式,并写出其对称中心;
(Ⅱ)若方程有实数解,求的取值范围.
20. 在中,角所对的边分别为,
(1)若,用表示;
(2)已知分别为的中点,若,求证:.
21. 如图,某超市的平面图为矩形ABCD,超市门EF在边AD上,其中
(1)求的正切值:
(2)若要在边上找一点安装安防摄像头,使得对超市门的摄像视角最大,求的长.
22. 已知函数在区间上有最大值4和最小值
(1)求?的值;
(2)设
①若时,,求实数的取值范围;
②若方程有三个不同的实数解,求实数的取值范围.
福州格致2020-2021学年度第三学段
高一数学半期考 答案版
考试时间:120分钟 全卷满分:150分
注意:本试卷包含I?II两卷.第I卷为选择题,所有答案必须用2B铅笔涂在答题卡中相应的位置.第1卷为非选择题,所有答案必须填在答题卷的相应位置.答案写在试卷上均无效
第I卷
一?单项选择题:本题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 若,且复数(为虚数单位)是纯虚数,则( )
A. B. C. D.
【答案】A
2. 在中,内角A,B,C所对的边分别为a,b,c,且,则
A. B. C. D.
【答案】A
3. 已知向量,则向量与向量的夹角为( )
A. B. C. D.
【答案】B
4. 己知向量,且,则( )
A. 5 B. C. D. 4
【答案】B
5. 小强同学在上完“三角函数图像与性质”后,兴致勃勃地画出函数的部分图像,如图所示.但粗心的他却标错了一个数据,已知轴上的数据完全正确.那么错误的数据是( )
A. B. C. D.
【答案】D
6. 如图是隋唐天坛,古叫圜丘,它位于唐长安城明德门遗址东约950米,即今西安市雁塔区陕西师范大学以南.天坛初建于隋而废弃于唐末,比北京明清天坛早1000多年,是隋唐王朝近三百年里的皇家祭天之处.某数学兴趣小组为了测得天坛的直径,在天坛外围测得米,米,米,,,据此可以估计天坛的最下面一层的直径大约为( ).(结果精确到1米)
(参考数据:,,,)
A. 39米 B. 43米 C. 49米 D. 53米
【答案】D
7. 已知函数,若,则( )
A. 等于 B. 等于 C. 等于 D. 无法确定
【答案】C
8. 中,角所对边分别为,且若,则的最大值是( )
A. B. C. 3 D.
【答案】A
二?多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求,全部选对的得5分,有选错的得0分,部分选对的得3分
9. 已知向量不共线,且,其中,若三点共线,则角的值可以是( )
A. B. C. D.
【答案】CD
10. 若△ABC内角A,B,C所对的边分别为a,b,c,且满足b﹣2a+4asin2=0,则下列结论正确的是( )
A. 角C一定为锐角 B. a2+2b2﹣c2=0
C. 3tanA+tanC=0 D. tanB的最小值为
【答案】BC
11. 已知函数,若,则下列不等式一定成立的有( )
A. B.
C. D.
【答案】BD
12. 已知是所在平面内一点,以下说法正确的是( )
A. 若动点满足,则点的轨迹一定通过的重心.
B. 若点满足,则点是垂心.
C. 若为的外心,且,则是的内心.
D. 若,则点为的外心
【答案】AD
三?填空题:本题共4小题,每小题5分,共20分.
13. 在复平面内,若数满足,则的最大值为__________.
【答案】
14. 中,内角对应的边分别为,若,,则的外接圆面积为__________.
【答案】
15. 定义在上的奇函数满足,且当时,,则函数在上的零点之和为____________.
【答案】6
16. 中,内角所对的边分别为的平分线交于点,且,若,则的最小值为__________.
【答案】16
四?解答题:本题共6小题,共70分.解答应写出文字说明?证明过程或演算步骤.
17. 中,角所对的边分别为,已知,
(1)求角的大小;
(2)若的面积为,求的周长.
【答案】(1);(2).
18. 中,角所对的边分别为,已知
(1)试判断的形状;
(2)若的周长为5,且,求.
【答案】(1)等腰三角形;(2)1.
19. 函数部分图象如图所示.
(Ⅰ)求函数的解析式,并写出其对称中心;
(Ⅱ)若方程有实数解,求的取值范围.
【答案】(Ⅰ) 函数的对称中心为(Ⅱ)
20. 在中,角所对的边分别为,
(1)若,用表示;
(2)已知分别为的中点,若,求证:.
【答案】(1);(2)证明见解析
21. 如图,某超市的平面图为矩形ABCD,超市门EF在边AD上,其中
(1)求的正切值:
(2)若要在边上找一点安装安防摄像头,使得对超市门的摄像视角最大,求的长.
【答案】(1);(2)m.
22. 已知函数在区间上有最大值4和最小值
(1)求?的值;
(2)设
①若时,,求实数的取值范围;
②若方程有三个不同的实数解,求实数的取值范围.
【答案】(1);(2)①;② .
同课章节目录
