山西省怀仁市2020-2021学年高二下学期期中考试数学(文)试题 Word版含答案
文档属性
| 名称 | 山西省怀仁市2020-2021学年高二下学期期中考试数学(文)试题 Word版含答案 | 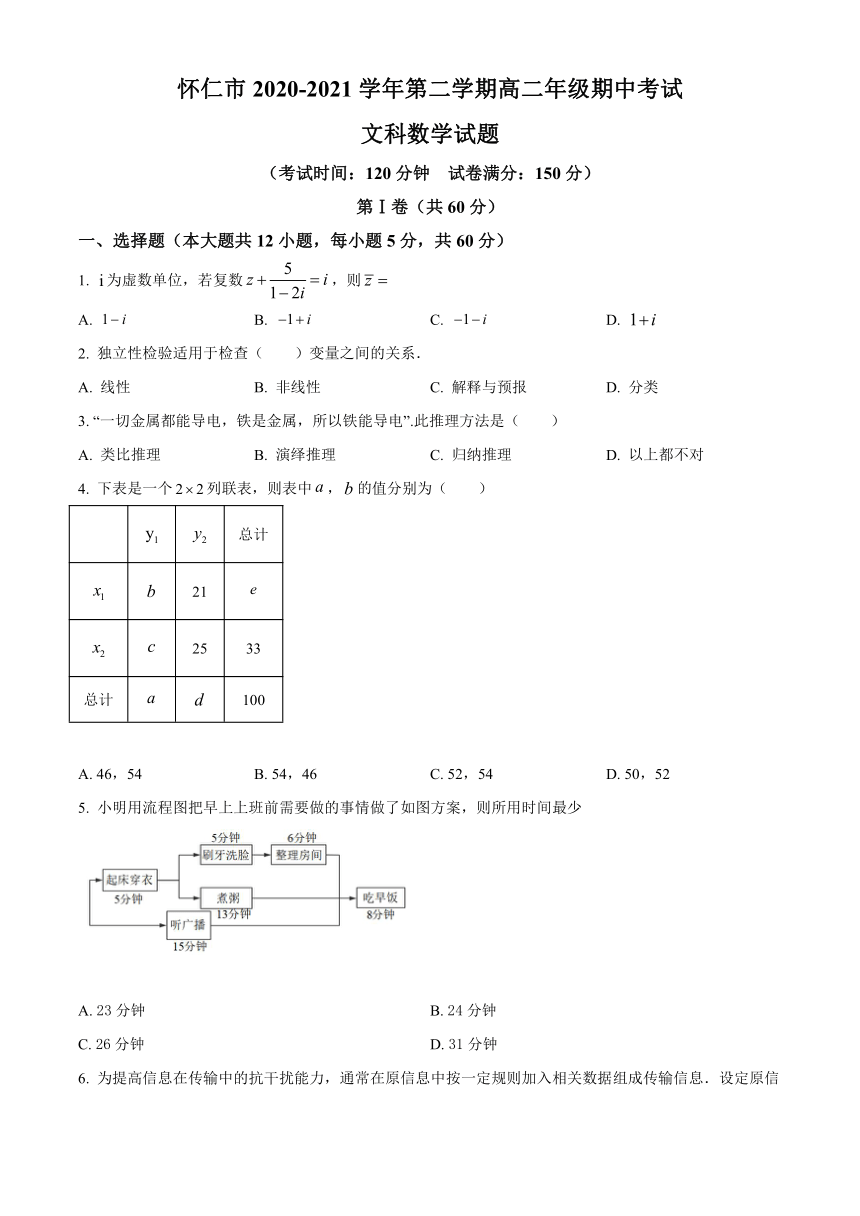 | |
| 格式 | doc | ||
| 文件大小 | 943.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-31 20:27:50 | ||
图片预览





文档简介
怀仁市2020-2021学年第二学期高二年级期中考试
文科数学试题
(考试时间:120分钟 试卷满分:150分)
第Ⅰ卷(共60分)
一、选择题(本大题共12小题,每小题5分,共60分)
1. 为虚数单位,若复数,则
A. B. C. D.
2. 独立性检验适用于检查( )变量之间的关系.
A. 线性 B. 非线性 C. 解释与预报 D. 分类
3. “一切金属都能导电,铁是金属,所以铁能导电”.此推理方法是( )
A. 类比推理 B. 演绎推理 C. 归纳推理 D. 以上都不对
4. 下表是一个列联表,则表中,值分别为( )
总计
21
25 33
总计
100
A. 46,54 B. 54,46 C. 52,54 D. 50,52
5. 小明用流程图把早上上班前需要做的事情做了如图方案,则所用时间最少
A. 23分钟 B. 24分钟
C. 26分钟 D. 31分钟
6. 为提高信息在传输中的抗干扰能力,通常在原信息中按一定规则加入相关数据组成传输信息.设定原信息为(),传输信息为,其中,运算规则为:,,,,例如原信息为111,则传输信息为01111.传输信息在传输过程中受到干扰可能导致接收信息出错,则下列接收信息一定有误的是
A. 11010 B. 01100 C. 10111 D. 00011
7. 已知变量之间的线性回归方程为且变量之间的一组相关数据如图所示,则下列说法错误的是( )
6 8 10 12
6
3 2
A. 变量x,y之间呈负相关关系
B. 可以预测,当时,
C.
D. 该回归直线必过点
8. 千百年来,我国劳动人民在生产实践中根据云的形状、走向、速度,厚度、颜色等的变化,总结了丰富的“看云识天气”的经验,并将这些经验编成谚语,如“天上钩钩云,地上雨淋淋”“日落云里走,雨在半夜后”……小波同学为了验证“日落云里走,雨在半夜后”,观察了地区的100天日落和夜晚天气,得到如下列联表.
单位:天
日落云里走 夜晚天气
下雨 未下雨
出现 25 5
未出现 25 45
临界值表:
0.05 0.010 0.001
3841 6.635 10.828
并计算得到,下列小波对地区天气的判断不正确的是( )
A. 夜晚下雨的概率约为
B. 未出现“日落云里走”,夜晚下雨的概率约为
C. 在犯错误的概率不超过0.001的前提下认为“日落云里走”是否出现与夜晚天气有关
D. 若出现“日落云里走”,则有99.9%的把握认为夜晚一定会下雨
9. 对大于或等于2的自然数的正整数幂运算有如下分解方式:
, ,
, ,
, ,
…… ……
根据上述分解规律,若,分解中最小的正整数是21,则等于( )
A. 8 B. 11 C. 12 D. 20
10. 设是复数,则下列命题中的假命题是
A. 若,则
B. 若,则
C. 若,则
D. 若,则
11. 中国古代制定乐律的生成方法是最早见于《管子·地员篇》的三分损益法,三分损益包含两个含义:三分损一和三分益一.根据某一特定的弦,去其,即三分损一,可得出该弦音的上方五度音;将该弦增长,即三分益一,可得出该弦音的下方四度音.中国古代的五声音阶:宫?徵(zhǐ),商?羽?角(jué),就是按三分损一和三分益一的顺序交替,连续使用产生的.若五音中的“宫”的律数为81,请根据上述律数演算法推算出“羽”的律数为( )
A. 72 B. 48 C. 54 D. 64
12. 设三边的长分别为,,,的面积为,其内切圆的半径为,则.类比这个结论可知:三棱锥的四个面的面积分别为,,,,内切球的半径为,三棱锥的体积为,则等于( )
A. B.
C. D.
第Ⅱ卷(共90分)
二、填空题(本大题共4小题,每小题5分,共20分)
13. 定义运算,则符合条件(是虚数单位)的复数的共轭复数对应的点在第________象限.
14. 极坐标系中,已知点,,则________.
15. 运行如图所示的程序框图,则输出的的值为________.
16. 公元前3世纪,古希腊数学家欧几里得在《几何原本》里提出:“球的体积与它的直径的立方成正比”,即,与此类似,我们可以得到:
(1)正四面体(所有棱长都相等的四面体)的体积与它的棱长的立方成正比,即;
(2)正方体的体积与它的棱长的立方成正比,即;
(3)正八面体(所有棱长都相等的八面体)的体积与它的棱长的立方成正比,即.
那么________.
三、解答题(本大题共6小题,共70分)
17. 观察:①;②.由上面两题的结构规律,你能否提出一个猜想?并证明你的猜想.
18. 已知复数z=a+i(a>0,a∈R),i为虚数单位,且复数为实数.
(1)求复数z;
(2)在复平面内,若复数(m+z)2对应的点在第一象限,求实数m的取值范围.
19. 在平面直角坐标系中,以坐标原点为极点,轴的正半轴为极轴建立极坐标系.已知点的极坐标为,直线的极坐标方程为,且点在直线上.
(1)求的值及直线的直角坐标方程;
(2)圆的极坐标方程为,试判断直线与圆的位置关系,并求出圆上的点到直线距离的最大值.
20. 为加强环境保护,治理空气污染,环境监测部门对某市空气质量进行调研,随机抽查了天空气中的和浓度(单位:),得下表:
32 18 4
6 8 12
3 7 10
(1)估计事件“该市一天空气中浓度不超过,且浓度不超过”的概率;
(2)根据所给数据,完成下面的列联表:
(3)根据(2)中的列联表,判断是否有的把握认为该市一天空气中浓度与浓度有关?
附:,
0.050 0.010 0.001
3.841 6.635 10.828
21. 双曲线与椭圆有许多优美的对称性质,对于双曲线(,),有下列性质:若是双曲线(,)不平行于对称轴且不过原点的弦,为的中点,为坐标原点,则为定值,椭圆也有类似的性质.若是椭圆不平行于对称轴且不过原点的弦,为的中点,为坐标原点,猜想的值,并证明.
22. 某公司对项目进行生产投资,所获得的利润有如下统计数据表:
项目投资金额(单位:百万元)
所获利润(单位:百万元)
(1)请用线性回归模型拟合与的关系,并用相关系数加以说明;
(2)该公司计划用百万元对、两个项目进行投资.若公司对项目投资百万元所获得的利润近似满足:,求、两个项目投资金额分别为多少时,获得的总利润最大?
附:①对于一组数据、、、,其回归直线方程的斜率和截距的最小二乘法估计公式分别为:,.
②线性相关系数.一般地,相关系数的绝对值在以上(含)认为线性相关性较强;否则,线性相关性较弱.
参考数据:对项目投资的统计数据表中,,.
怀仁市2020-2021学年第二学期高二年级期中考试
文科数学试题 答案版
(考试时间:120分钟 试卷满分:150分)
第Ⅰ卷(共60分)
一、选择题(本大题共12小题,每小题5分,共60分)
1. 为虚数单位,若复数,则
A. B. C. D.
【答案】B
2. 独立性检验适用于检查( )变量之间的关系.
A. 线性 B. 非线性 C. 解释与预报 D. 分类
【答案】D
3. “一切金属都能导电,铁是金属,所以铁能导电”.此推理方法是( )
A. 类比推理 B. 演绎推理 C. 归纳推理 D. 以上都不对
【答案】B
4. 下表是一个列联表,则表中,值分别为( )
总计
21
25 33
总计
100
A. 46,54 B. 54,46 C. 52,54 D. 50,52
【答案】B
5. 小明用流程图把早上上班前需要做的事情做了如图方案,则所用时间最少
A. 23分钟 B. 24分钟
C. 26分钟 D. 31分钟
【答案】C
6. 为提高信息在传输中的抗干扰能力,通常在原信息中按一定规则加入相关数据组成传输信息.设定原信息为(),传输信息为,其中,运算规则为:,,,,例如原信息为111,则传输信息为01111.传输信息在传输过程中受到干扰可能导致接收信息出错,则下列接收信息一定有误的是
A. 11010 B. 01100 C. 10111 D. 00011
【答案】C
7. 已知变量之间的线性回归方程为且变量之间的一组相关数据如图所示,则下列说法错误的是( )
6 8 10 12
6
3 2
A. 变量x,y之间呈负相关关系
B. 可以预测,当时,
C.
D. 该回归直线必过点
【答案】C
8. 千百年来,我国劳动人民在生产实践中根据云的形状、走向、速度,厚度、颜色等的变化,总结了丰富的“看云识天气”的经验,并将这些经验编成谚语,如“天上钩钩云,地上雨淋淋”“日落云里走,雨在半夜后”……小波同学为了验证“日落云里走,雨在半夜后”,观察了地区的100天日落和夜晚天气,得到如下列联表.
单位:天
日落云里走 夜晚天气
下雨 未下雨
出现 25 5
未出现 25 45
临界值表:
0.05 0.010 0.001
3841 6.635 10.828
并计算得到,下列小波对地区天气的判断不正确的是( )
A. 夜晚下雨的概率约为
B. 未出现“日落云里走”,夜晚下雨的概率约为
C. 在犯错误的概率不超过0.001的前提下认为“日落云里走”是否出现与夜晚天气有关
D. 若出现“日落云里走”,则有99.9%的把握认为夜晚一定会下雨
【答案】D
9. 对大于或等于2的自然数的正整数幂运算有如下分解方式:
, ,
, ,
, ,
…… ……
根据上述分解规律,若,分解中最小的正整数是21,则等于( )
A. 8 B. 11 C. 12 D. 20
【答案】B
10. 设是复数,则下列命题中的假命题是
A. 若,则
B. 若,则
C. 若,则
D. 若,则
【答案】D
11. 中国古代制定乐律的生成方法是最早见于《管子·地员篇》的三分损益法,三分损益包含两个含义:三分损一和三分益一.根据某一特定的弦,去其,即三分损一,可得出该弦音的上方五度音;将该弦增长,即三分益一,可得出该弦音的下方四度音.中国古代的五声音阶:宫?徵(zhǐ),商?羽?角(jué),就是按三分损一和三分益一的顺序交替,连续使用产生的.若五音中的“宫”的律数为81,请根据上述律数演算法推算出“羽”的律数为( )
A. 72 B. 48 C. 54 D. 64
【答案】B
12. 设三边的长分别为,,,的面积为,其内切圆的半径为,则.类比这个结论可知:三棱锥的四个面的面积分别为,,,,内切球的半径为,三棱锥的体积为,则等于( )
A. B.
C. D.
【答案】C
第Ⅱ卷(共90分)
二、填空题(本大题共4小题,每小题5分,共20分)
13. 定义运算,则符合条件(是虚数单位)的复数的共轭复数对应的点在第________象限.
【答案】二
14. 极坐标系中,已知点,,则________.
【答案】10
15. 运行如图所示的程序框图,则输出的的值为________.
【答案】
16. 公元前3世纪,古希腊数学家欧几里得在《几何原本》里提出:“球的体积与它的直径的立方成正比”,即,与此类似,我们可以得到:
(1)正四面体(所有棱长都相等的四面体)的体积与它的棱长的立方成正比,即;
(2)正方体的体积与它的棱长的立方成正比,即;
(3)正八面体(所有棱长都相等的八面体)的体积与它的棱长的立方成正比,即.
那么________.
【答案】
三、解答题(本大题共6小题,共70分)
17. 观察:①;②.由上面两题的结构规律,你能否提出一个猜想?并证明你的猜想.
【答案】答案见解析.
18. 已知复数z=a+i(a>0,a∈R),i为虚数单位,且复数为实数.
(1)求复数z;
(2)在复平面内,若复数(m+z)2对应的点在第一象限,求实数m的取值范围.
【答案】(1);(2).
19. 在平面直角坐标系中,以坐标原点为极点,轴的正半轴为极轴建立极坐标系.已知点的极坐标为,直线的极坐标方程为,且点在直线上.
(1)求的值及直线的直角坐标方程;
(2)圆的极坐标方程为,试判断直线与圆的位置关系,并求出圆上的点到直线距离的最大值.
【答案】(1),;(2).
20. 为加强环境保护,治理空气污染,环境监测部门对某市空气质量进行调研,随机抽查了天空气中的和浓度(单位:),得下表:
32 18 4
6 8 12
3 7 10
(1)估计事件“该市一天空气中浓度不超过,且浓度不超过”的概率;
(2)根据所给数据,完成下面的列联表:
(3)根据(2)中的列联表,判断是否有的把握认为该市一天空气中浓度与浓度有关?
附:,
0.050 0.010 0.001
3.841 6.635 10.828
【答案】(1);(2)答案见解析;(3)有.
21. 双曲线与椭圆有许多优美的对称性质,对于双曲线(,),有下列性质:若是双曲线(,)不平行于对称轴且不过原点的弦,为的中点,为坐标原点,则为定值,椭圆也有类似的性质.若是椭圆不平行于对称轴且不过原点的弦,为的中点,为坐标原点,猜想的值,并证明.
【答案】;证明见解析.
22. 某公司对项目进行生产投资,所获得的利润有如下统计数据表:
项目投资金额(单位:百万元)
所获利润(单位:百万元)
(1)请用线性回归模型拟合与的关系,并用相关系数加以说明;
(2)该公司计划用百万元对、两个项目进行投资.若公司对项目投资百万元所获得的利润近似满足:,求、两个项目投资金额分别为多少时,获得的总利润最大?
附:①对于一组数据、、、,其回归直线方程的斜率和截距的最小二乘法估计公式分别为:,.
②线性相关系数.一般地,相关系数的绝对值在以上(含)认为线性相关性较强;否则,线性相关性较弱.
参考数据:对项目投资的统计数据表中,,.
【答案】(1);答案见解析;(2)对、项目分别投资百万元,百万元时,获得总利润最大.
文科数学试题
(考试时间:120分钟 试卷满分:150分)
第Ⅰ卷(共60分)
一、选择题(本大题共12小题,每小题5分,共60分)
1. 为虚数单位,若复数,则
A. B. C. D.
2. 独立性检验适用于检查( )变量之间的关系.
A. 线性 B. 非线性 C. 解释与预报 D. 分类
3. “一切金属都能导电,铁是金属,所以铁能导电”.此推理方法是( )
A. 类比推理 B. 演绎推理 C. 归纳推理 D. 以上都不对
4. 下表是一个列联表,则表中,值分别为( )
总计
21
25 33
总计
100
A. 46,54 B. 54,46 C. 52,54 D. 50,52
5. 小明用流程图把早上上班前需要做的事情做了如图方案,则所用时间最少
A. 23分钟 B. 24分钟
C. 26分钟 D. 31分钟
6. 为提高信息在传输中的抗干扰能力,通常在原信息中按一定规则加入相关数据组成传输信息.设定原信息为(),传输信息为,其中,运算规则为:,,,,例如原信息为111,则传输信息为01111.传输信息在传输过程中受到干扰可能导致接收信息出错,则下列接收信息一定有误的是
A. 11010 B. 01100 C. 10111 D. 00011
7. 已知变量之间的线性回归方程为且变量之间的一组相关数据如图所示,则下列说法错误的是( )
6 8 10 12
6
3 2
A. 变量x,y之间呈负相关关系
B. 可以预测,当时,
C.
D. 该回归直线必过点
8. 千百年来,我国劳动人民在生产实践中根据云的形状、走向、速度,厚度、颜色等的变化,总结了丰富的“看云识天气”的经验,并将这些经验编成谚语,如“天上钩钩云,地上雨淋淋”“日落云里走,雨在半夜后”……小波同学为了验证“日落云里走,雨在半夜后”,观察了地区的100天日落和夜晚天气,得到如下列联表.
单位:天
日落云里走 夜晚天气
下雨 未下雨
出现 25 5
未出现 25 45
临界值表:
0.05 0.010 0.001
3841 6.635 10.828
并计算得到,下列小波对地区天气的判断不正确的是( )
A. 夜晚下雨的概率约为
B. 未出现“日落云里走”,夜晚下雨的概率约为
C. 在犯错误的概率不超过0.001的前提下认为“日落云里走”是否出现与夜晚天气有关
D. 若出现“日落云里走”,则有99.9%的把握认为夜晚一定会下雨
9. 对大于或等于2的自然数的正整数幂运算有如下分解方式:
, ,
, ,
, ,
…… ……
根据上述分解规律,若,分解中最小的正整数是21,则等于( )
A. 8 B. 11 C. 12 D. 20
10. 设是复数,则下列命题中的假命题是
A. 若,则
B. 若,则
C. 若,则
D. 若,则
11. 中国古代制定乐律的生成方法是最早见于《管子·地员篇》的三分损益法,三分损益包含两个含义:三分损一和三分益一.根据某一特定的弦,去其,即三分损一,可得出该弦音的上方五度音;将该弦增长,即三分益一,可得出该弦音的下方四度音.中国古代的五声音阶:宫?徵(zhǐ),商?羽?角(jué),就是按三分损一和三分益一的顺序交替,连续使用产生的.若五音中的“宫”的律数为81,请根据上述律数演算法推算出“羽”的律数为( )
A. 72 B. 48 C. 54 D. 64
12. 设三边的长分别为,,,的面积为,其内切圆的半径为,则.类比这个结论可知:三棱锥的四个面的面积分别为,,,,内切球的半径为,三棱锥的体积为,则等于( )
A. B.
C. D.
第Ⅱ卷(共90分)
二、填空题(本大题共4小题,每小题5分,共20分)
13. 定义运算,则符合条件(是虚数单位)的复数的共轭复数对应的点在第________象限.
14. 极坐标系中,已知点,,则________.
15. 运行如图所示的程序框图,则输出的的值为________.
16. 公元前3世纪,古希腊数学家欧几里得在《几何原本》里提出:“球的体积与它的直径的立方成正比”,即,与此类似,我们可以得到:
(1)正四面体(所有棱长都相等的四面体)的体积与它的棱长的立方成正比,即;
(2)正方体的体积与它的棱长的立方成正比,即;
(3)正八面体(所有棱长都相等的八面体)的体积与它的棱长的立方成正比,即.
那么________.
三、解答题(本大题共6小题,共70分)
17. 观察:①;②.由上面两题的结构规律,你能否提出一个猜想?并证明你的猜想.
18. 已知复数z=a+i(a>0,a∈R),i为虚数单位,且复数为实数.
(1)求复数z;
(2)在复平面内,若复数(m+z)2对应的点在第一象限,求实数m的取值范围.
19. 在平面直角坐标系中,以坐标原点为极点,轴的正半轴为极轴建立极坐标系.已知点的极坐标为,直线的极坐标方程为,且点在直线上.
(1)求的值及直线的直角坐标方程;
(2)圆的极坐标方程为,试判断直线与圆的位置关系,并求出圆上的点到直线距离的最大值.
20. 为加强环境保护,治理空气污染,环境监测部门对某市空气质量进行调研,随机抽查了天空气中的和浓度(单位:),得下表:
32 18 4
6 8 12
3 7 10
(1)估计事件“该市一天空气中浓度不超过,且浓度不超过”的概率;
(2)根据所给数据,完成下面的列联表:
(3)根据(2)中的列联表,判断是否有的把握认为该市一天空气中浓度与浓度有关?
附:,
0.050 0.010 0.001
3.841 6.635 10.828
21. 双曲线与椭圆有许多优美的对称性质,对于双曲线(,),有下列性质:若是双曲线(,)不平行于对称轴且不过原点的弦,为的中点,为坐标原点,则为定值,椭圆也有类似的性质.若是椭圆不平行于对称轴且不过原点的弦,为的中点,为坐标原点,猜想的值,并证明.
22. 某公司对项目进行生产投资,所获得的利润有如下统计数据表:
项目投资金额(单位:百万元)
所获利润(单位:百万元)
(1)请用线性回归模型拟合与的关系,并用相关系数加以说明;
(2)该公司计划用百万元对、两个项目进行投资.若公司对项目投资百万元所获得的利润近似满足:,求、两个项目投资金额分别为多少时,获得的总利润最大?
附:①对于一组数据、、、,其回归直线方程的斜率和截距的最小二乘法估计公式分别为:,.
②线性相关系数.一般地,相关系数的绝对值在以上(含)认为线性相关性较强;否则,线性相关性较弱.
参考数据:对项目投资的统计数据表中,,.
怀仁市2020-2021学年第二学期高二年级期中考试
文科数学试题 答案版
(考试时间:120分钟 试卷满分:150分)
第Ⅰ卷(共60分)
一、选择题(本大题共12小题,每小题5分,共60分)
1. 为虚数单位,若复数,则
A. B. C. D.
【答案】B
2. 独立性检验适用于检查( )变量之间的关系.
A. 线性 B. 非线性 C. 解释与预报 D. 分类
【答案】D
3. “一切金属都能导电,铁是金属,所以铁能导电”.此推理方法是( )
A. 类比推理 B. 演绎推理 C. 归纳推理 D. 以上都不对
【答案】B
4. 下表是一个列联表,则表中,值分别为( )
总计
21
25 33
总计
100
A. 46,54 B. 54,46 C. 52,54 D. 50,52
【答案】B
5. 小明用流程图把早上上班前需要做的事情做了如图方案,则所用时间最少
A. 23分钟 B. 24分钟
C. 26分钟 D. 31分钟
【答案】C
6. 为提高信息在传输中的抗干扰能力,通常在原信息中按一定规则加入相关数据组成传输信息.设定原信息为(),传输信息为,其中,运算规则为:,,,,例如原信息为111,则传输信息为01111.传输信息在传输过程中受到干扰可能导致接收信息出错,则下列接收信息一定有误的是
A. 11010 B. 01100 C. 10111 D. 00011
【答案】C
7. 已知变量之间的线性回归方程为且变量之间的一组相关数据如图所示,则下列说法错误的是( )
6 8 10 12
6
3 2
A. 变量x,y之间呈负相关关系
B. 可以预测,当时,
C.
D. 该回归直线必过点
【答案】C
8. 千百年来,我国劳动人民在生产实践中根据云的形状、走向、速度,厚度、颜色等的变化,总结了丰富的“看云识天气”的经验,并将这些经验编成谚语,如“天上钩钩云,地上雨淋淋”“日落云里走,雨在半夜后”……小波同学为了验证“日落云里走,雨在半夜后”,观察了地区的100天日落和夜晚天气,得到如下列联表.
单位:天
日落云里走 夜晚天气
下雨 未下雨
出现 25 5
未出现 25 45
临界值表:
0.05 0.010 0.001
3841 6.635 10.828
并计算得到,下列小波对地区天气的判断不正确的是( )
A. 夜晚下雨的概率约为
B. 未出现“日落云里走”,夜晚下雨的概率约为
C. 在犯错误的概率不超过0.001的前提下认为“日落云里走”是否出现与夜晚天气有关
D. 若出现“日落云里走”,则有99.9%的把握认为夜晚一定会下雨
【答案】D
9. 对大于或等于2的自然数的正整数幂运算有如下分解方式:
, ,
, ,
, ,
…… ……
根据上述分解规律,若,分解中最小的正整数是21,则等于( )
A. 8 B. 11 C. 12 D. 20
【答案】B
10. 设是复数,则下列命题中的假命题是
A. 若,则
B. 若,则
C. 若,则
D. 若,则
【答案】D
11. 中国古代制定乐律的生成方法是最早见于《管子·地员篇》的三分损益法,三分损益包含两个含义:三分损一和三分益一.根据某一特定的弦,去其,即三分损一,可得出该弦音的上方五度音;将该弦增长,即三分益一,可得出该弦音的下方四度音.中国古代的五声音阶:宫?徵(zhǐ),商?羽?角(jué),就是按三分损一和三分益一的顺序交替,连续使用产生的.若五音中的“宫”的律数为81,请根据上述律数演算法推算出“羽”的律数为( )
A. 72 B. 48 C. 54 D. 64
【答案】B
12. 设三边的长分别为,,,的面积为,其内切圆的半径为,则.类比这个结论可知:三棱锥的四个面的面积分别为,,,,内切球的半径为,三棱锥的体积为,则等于( )
A. B.
C. D.
【答案】C
第Ⅱ卷(共90分)
二、填空题(本大题共4小题,每小题5分,共20分)
13. 定义运算,则符合条件(是虚数单位)的复数的共轭复数对应的点在第________象限.
【答案】二
14. 极坐标系中,已知点,,则________.
【答案】10
15. 运行如图所示的程序框图,则输出的的值为________.
【答案】
16. 公元前3世纪,古希腊数学家欧几里得在《几何原本》里提出:“球的体积与它的直径的立方成正比”,即,与此类似,我们可以得到:
(1)正四面体(所有棱长都相等的四面体)的体积与它的棱长的立方成正比,即;
(2)正方体的体积与它的棱长的立方成正比,即;
(3)正八面体(所有棱长都相等的八面体)的体积与它的棱长的立方成正比,即.
那么________.
【答案】
三、解答题(本大题共6小题,共70分)
17. 观察:①;②.由上面两题的结构规律,你能否提出一个猜想?并证明你的猜想.
【答案】答案见解析.
18. 已知复数z=a+i(a>0,a∈R),i为虚数单位,且复数为实数.
(1)求复数z;
(2)在复平面内,若复数(m+z)2对应的点在第一象限,求实数m的取值范围.
【答案】(1);(2).
19. 在平面直角坐标系中,以坐标原点为极点,轴的正半轴为极轴建立极坐标系.已知点的极坐标为,直线的极坐标方程为,且点在直线上.
(1)求的值及直线的直角坐标方程;
(2)圆的极坐标方程为,试判断直线与圆的位置关系,并求出圆上的点到直线距离的最大值.
【答案】(1),;(2).
20. 为加强环境保护,治理空气污染,环境监测部门对某市空气质量进行调研,随机抽查了天空气中的和浓度(单位:),得下表:
32 18 4
6 8 12
3 7 10
(1)估计事件“该市一天空气中浓度不超过,且浓度不超过”的概率;
(2)根据所给数据,完成下面的列联表:
(3)根据(2)中的列联表,判断是否有的把握认为该市一天空气中浓度与浓度有关?
附:,
0.050 0.010 0.001
3.841 6.635 10.828
【答案】(1);(2)答案见解析;(3)有.
21. 双曲线与椭圆有许多优美的对称性质,对于双曲线(,),有下列性质:若是双曲线(,)不平行于对称轴且不过原点的弦,为的中点,为坐标原点,则为定值,椭圆也有类似的性质.若是椭圆不平行于对称轴且不过原点的弦,为的中点,为坐标原点,猜想的值,并证明.
【答案】;证明见解析.
22. 某公司对项目进行生产投资,所获得的利润有如下统计数据表:
项目投资金额(单位:百万元)
所获利润(单位:百万元)
(1)请用线性回归模型拟合与的关系,并用相关系数加以说明;
(2)该公司计划用百万元对、两个项目进行投资.若公司对项目投资百万元所获得的利润近似满足:,求、两个项目投资金额分别为多少时,获得的总利润最大?
附:①对于一组数据、、、,其回归直线方程的斜率和截距的最小二乘法估计公式分别为:,.
②线性相关系数.一般地,相关系数的绝对值在以上(含)认为线性相关性较强;否则,线性相关性较弱.
参考数据:对项目投资的统计数据表中,,.
【答案】(1);答案见解析;(2)对、项目分别投资百万元,百万元时,获得总利润最大.
同课章节目录
