江苏省南京29中学2020-2021学年高一下学期6月学情检测数学试题 Word版含答案
文档属性
| 名称 | 江苏省南京29中学2020-2021学年高一下学期6月学情检测数学试题 Word版含答案 |  | |
| 格式 | docx | ||
| 文件大小 | 426.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-01 08:14:47 | ||
图片预览




文档简介
南京市第二十九中学2020-2021学年下高一6月学情检测2021.6
数 学
一?单项选择题:本大题共8小题,每小题5分,共计40分.在每小题给出的四个选项中,只有一项符合题目要求,请把答案填涂在答题卡相应位置.
1. 已知i为虚数单位,复数z满足z= ,则||=( )
A. B. C. D.
4084320457202. 某部门为了了解一批树苗的生长情况,在3000
棵树苗中随机抽取200棵,统计这200棵树苗
的高度,并绘制了频率分布直方图(如图),那么
根据该图可推测,在这3000棵树苗中高度小于
100cm的树苗棵数是( ).
A.360 B.600
C.840 D.1320
3. 已知m,n表示两条不同直线,α表示平面,下列说法正确的是( )
A.若m//α,n//α,则m//n B.若m⊥α,nα,则m⊥n
C.若m⊥α,m⊥n,则n//α D.若m//α,m⊥n,则n⊥α
4.已知在△ABC中,AB=2,AC=3,∠BAC=,点D为边BC上靠近B的三等分点,则·的值为( )
A.- B.- C. D.53390806485890(第5题)
(第5题)
410273520955055594257418070(第5题)
(第5题)
5.如图,棱锥D′-A′CD体积与长方体ABCD-A′B′C′D′体积的比值为( )53390806485890(第5题)
(第5题)
A. B. C. D.
6.若λsin160°+tan20°=,则实数λ的值为( )
A.3 B. C.2 D.4
49815756648457. 埃及胡夫金字塔是古代世界建筑奇迹之一,它的形状可视为一个正四棱锥,以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积,则其侧面三角形底边上的高与底面正方形的边长的比值为( )
A. B. C. D.
8.已知菱形ABCD边长为2,∠ABC=60?,沿对角线AC折叠成三棱锥B’-ACD,使得二面角
B'-AC-D为60°,设E为B’C的中点,F为三棱锥B'-ACD表面上的动点,且总满足AC⊥EF,则点F轨迹的长度为( )
A.2 B.3 C. D.
二?多项选择题:本大题共4小题,每小题5分,共计20分.在每小题给出的四个选项中,有多项符合题目要求,全部选对得5分,部分选对得2分,不选或有选错的得0分.请把答案填涂在答题卡相应位置.
9.下列命题中,真命题有 ( )
A.如果两个平面有三个不在一条直线上的公共点,那么这两个平面重合
B.两条直线可以确定一个平面
C.空间中,相交于同一点的三条直线在同一平面内
D.若M∈α,M∈β,α∩β=l,则M∈l
450088026860510.如图,在平面四边形ABCD中,已知∠B+∠D=180°,AB=2,
BC=4,CD=4,AD=2,下列四个结论中正确的是( )
A.∠B=∠D=90° B.四边形ABCD的面积为4+
C.AC=6 D.四边形ABCD的周长为6+4+2
11.z=1+cos2θ+isin2θ(-<θ<)(其中i为虚数单位)下列说法正确的是( )
A.复数z在复平面上对应的点可能落在第二象限 B.z可能为实数
C.|z|=2cosθ D.的实部为
12.如图所示,在正△ABC中,D,E分别为边AB,AC的中点,其中AB=8,将△ADE沿DE翻折至A'DE位置,使得二面角A'-DE-B为60°,则下列选项中正确的是( )
323088011430A.点A' 到平面BCED的距离为3
B.直线A'D与直线CE所成的角的余弦值为
C.A'D⊥BD
D. 四棱锥A' -BCED的外接球半径为
三?填空题:本题共4小题,每小题5分,共20分.其中第16题第一空3分,第二空2分.请把答案填写在答题卡相应位置.
13.一圆锥侧面展开图为半径为8的半圆,则此圆锥的体积为______.
14.某企业三月中旬生产A,B,C三种产品共3 000件,根据分层抽样的结果,企业统计员制作了如下的表格:
产品类别
A
B
C
产品数量(件)
1300
样本数量(件)
130
由于不小心,表格中A,C产品的有关数据已被污染看不清楚,统计员记的A产品的样本数
量比C产品的样本数量多10,根据以上信息,可得C产品的数量是________.
15.在△ABC中,已知AB=4,AC=3,P是边BC的垂直平分线上的一点,则·=
___________.
16.蹴鞠(如图所示),又名蹴球,蹴圆,筑圆,踢圆等,蹴有用脚蹴?踢?蹋的含义;鞠最早系
外包皮革?内实米糠的球.因而蹴鞠就是指古人以交蹴?蹋?踢皮球的活动,类似于今日的
足球.早在2006年5月,蹴鞠已作为非物质文化遗产经国务院批准列入第一批国家非物
质文化遗产名录.现已知某蹴鞠的表面上有四个点S?A?B?C,满足S-ABC是正三棱锥,
M3958590179705是SB的中点,CM⊥SA,侧棱长为2,则该蹴鞠的体积为__________;蹴鞠球心到平面
ABC的距离为____________.
四?解答题:本题共6小题,共70分.请在答题卡指定区域内作答,解答时应写出必要的文字说明,证明过程或演算步骤.
17.(本小题满分10分)
已知函数f(x)=2cos2+sinx.
(1)求函数f(x)在区间[0,π]上的单调增区间;
(2)当f(α)= ,且α∈(-, ) ,求sin(2α+) 的值.
18.(本小题满分12分)
3550285170180A
B
C
D
D1
A1
B1
C1
P
(第18题图)
A
B
C
D
D1
A1
B1
C1
P
(第18题图)
如图,在长方体ABCD-A1B1C1D1中,已知底面ABCD是正方形,点P是侧棱CC1上的一点.
(1)求证BD⊥A1P;
(2)若AC1//平面PBD,求的值.
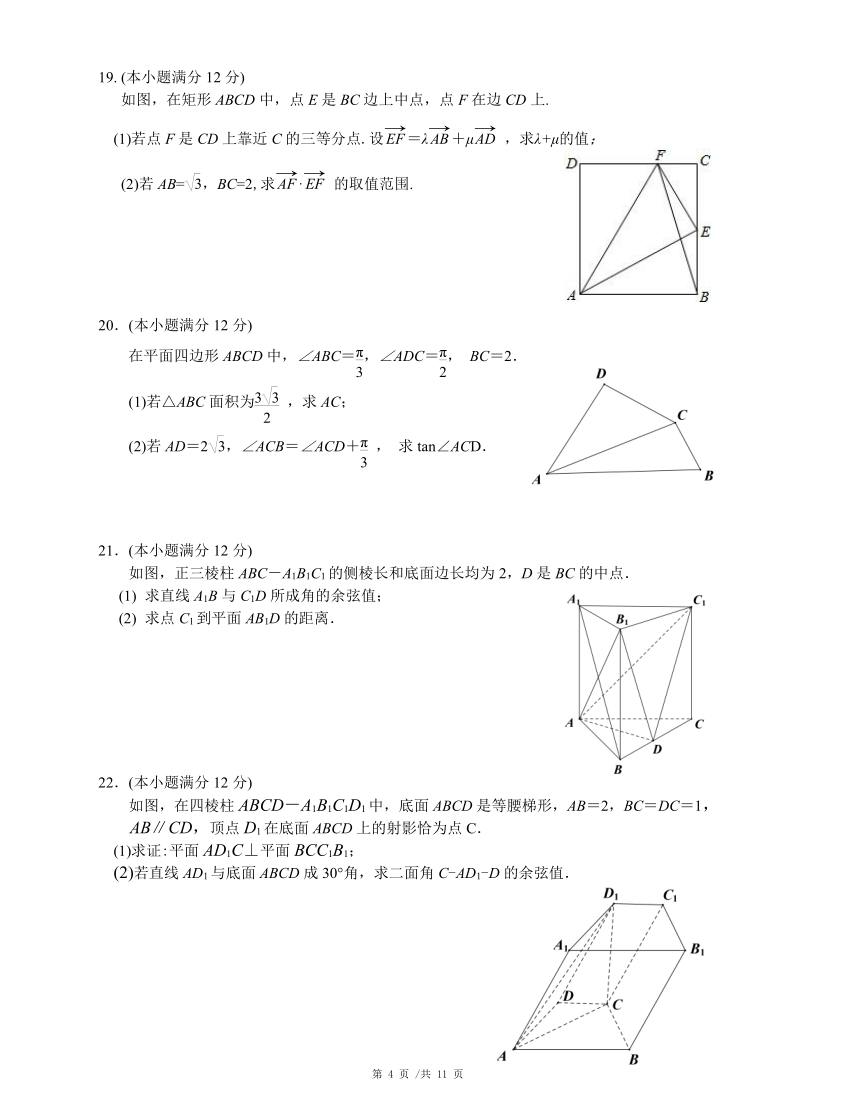
19. (本小题满分12分)
如图,在矩形ABCD中,点E是BC边上中点,点F在边CD上.
4101465332740(1)若点F是CD上靠近C的三等分点.设=λ+μ ,求λ+μ的值;
(2)若AB=,BC=2,求· 的取值范围.
20.(本小题满分12分)
3768090208915在平面四边形ABCD中,∠ABC=,∠ADC=, BC=2.
(1)若△ABC面积为 ,求AC;
(2)若AD=2,∠ACB=∠ACD+ , 求tan∠ACD.
21.(本小题满分12分)
如图,正三棱柱ABC-A1B1C1的侧棱长和底面边长均为2,D是BC的中点.
406336520320求直线A1B与C1D所成角的余弦值;
求点C1到平面AB1D的距离.
22.(本小题满分12分)
如图,在四棱柱ABCD-A1B1C1D1中,底面ABCD是等腰梯形,AB=2,BC=DC=1,
AB∥CD,顶点D1在底面ABCD上的射影恰为点C.
(1)求证:平面AD1C⊥平面BCC1B1;
3455035158750(2)若直线AD1与底面ABCD成30°角,求二面角C-AD1-D的余弦值.
南京市第二十九中学2020-2021学年下高一6月学情检测2021.6
参考答案与评分标准
一、单项选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.D 2.B 3.B 4.D 5.C 6.D 7.C 8.D
二、多项选择题:本大题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求的.全部选对的得5分,部分选对的得2分,有选错的得0分.
9. AD 10.ACD 11.BCD 12.ABD
三、填空题:本大题共4小题,每小题5分,共20分.
13. 14.800 15.- 16.4π ,
四、解答题:本大题共6小题,共70分.
17.(本小题满分10分)
(1) f(x)=cosx+1+sinx=2sin(x+)+1 ……………………………………………1分
令-+2kπ≤x+≤+2kπ, k∈Z
得-+2kπ≤x≤+2kπ, k∈Z ……………………………………………3分
令k=0, 则-≤x≤, ……………………………………………4分
∴函数f(x)在区间[0,π]上的单调增区间为[0,] ………………………………5分
(2)由f(α)=,得2 sin(α+)+1= ,
∴sin(α+)= ………………………………………………………………7分
又∵α∈(-, ) , ∴-<α+<
∴cos(α+)=== ………………………………………9分
∴sin(2α+)=sin[2(α+)]=2sin(α+)cos(α+)=2··=. ………………10分
18.(本小题满分12分)
(1)连接A1C1.
因为ABCD-A1B1C1D1为长方体,所以侧棱C1C⊥平面ABCD.
又BD平面ABCD,所以CC1⊥BD. ……………………………………………2分
因为底面ABCD是正方形,所以AC⊥BD.
又AC∩CC1=C,AC面ACC1A1,CC1面ACC1A1,
所以BD⊥面ACC1A1. …………………………………………………4分
又因为A1P面ACC1A1,所以BD⊥A1P. …………………………………………6分
(2)连接AC交BD于点O,连接OP.
因为AC1//平面PBD,AC1平面ACC1,
3774440-567055O
A
B
C
D
D1
A1
B1
C1
P
(第18题图)
O
A
B
C
D
D1
A1
B1
C1
P
(第18题图)
平面ACC1∩平面BDP=OP,
所以AC1//OP. ………………………9分
因为四边形ABCD是正方形,对角线AC交BD于点O,
所以点O是AC的中点,所以AO=OC,
所以在△ACC1中,==1. …………12分
19.(本小题满分12分)
(1) ∵=-=-+,……………………………………………2分
又=λ+μ ,
且,不共线 ,
∴λ=-,μ= , ……………………………………………………………4分
∴λ+μ=-+= . …………………………………………………………5分
(不交代 , 不共线扣1分)
(2)以A为原点,以AB、AD所在直线为x轴、y轴,建立如图所示的平面直角坐标系,
∵AB=,BC=2,
∴B( , 0) , D(0 , 2) , C ( , 2) , E( , 1) ;
设F(x , 2) , x∈[0, ],
则=(x,2),=(x-,1) ,
∴·=x2-x+2=(x-)2+ , x∈[0, ] ;……………………………9分
当x=时,·的最小值为;
当x=0或时,·的最大值为2;
∴·的取值范围为[ , 2] . ……………………………………………………12分
20.(本小题满分12分)
(1)在△ABC中,∠ABC= , BC=2 ,
∴SΔABC=AB·BC·sin∠BAC= ,
∴AB=3; …………………………………………………………………………2分
在△ABC中,由余弦定理得,
AC2=AB2+BC2-2AB·BC·cos∠ABC=9+4-2×3×2×=7,
∴AC= . …………………………………………………………………………5分
(至少出现一次“在△ABC”中,否则扣1分)
(使用余弦定理时,必须先默公式,再代数值,最后得结果,否则扣1分)
3961765187960(2)设∠ACD=α , 则∠ACB=α+ ;
在Rt△ACD中,AD=2,
∴AC==, ……………………………………7分
在△ABC中,∠BAC=π-∠ACB-ABC=-α ,
由正弦定理得,=
∴= ; ………………………………………………………9分
∴2sinα=cosα , ∴tanα=
∴tan∠ACD=…………………………………………………………………12分
21.(本小题满分12分)
(1)法一:连接A1C, 交AC1于点E,连接DE.
在三棱柱ABC-A1B1C1中,四边形ACC1A1为平行四边形,
4082415-78740 ∴E是A1C的中点……………………………………2分
在△A1BC中,D、E分别是BC、A1C的中点,
∴DE∥A1B…………………………………………………4分
∴∠EDC1(或其补角)即为直线A1B和C1D所成的角
在△EDC1中, ED=, DC1= , C1E= ,
由余弦定理,cos∠EDC1==
∴直线A1B和C1D所成的角的余弦值为.………………………………6分
法二:取B1C1的中点F,连接BF、A1F
4034790188595在三棱柱ABC-A1B1C1中,BC B1C1
∵D、F分别是BC、 B1C1的中点,
∴BDFC1……………………………………………………2分
∴四边形BDC1F为平行四边形
∴BF∥DC1……………………………………………………4分
∴∠FBA1(或其补角)即为直线A1B和C1D所成的角
在△FBA1中,BA1=2, BF=, A1F=,
由余弦定理,cos∠FBA1= = .
∴直线A1B和C1D所成的角的余弦值为.………………………………6分
法三:将正三棱柱ABC-A1B1C1补成如图所示的直平行六面体ABGC- A1B1G1C1
连接C1G、DG
3853815136525 则A1B∥C1G…………………………………4分
∴∠DC1G(或其补角)即为直线A1B和C1D所成的角
在△DC1G中,DC1=, C1G=2,DG=,
由余弦定理,cos∠DC1G= = .
∴直线A1B和C1D所成的角的余弦值为.………………6分
(未指出“………即为直线A1B和DC1所成的角”扣1分)
3777615-43180(2) 法一:过C1作C1H⊥B1D, 垂足为H
在正三棱柱ABC-A1B1C1中,
C1C⊥平面ABC,AD平面ABC,
∴C1C⊥ AD
在△ABC中,AB=AC, BD=CD,
∴AD⊥ BC
且BC∩C1C= C
BC、C1C平面BCC1B1
∴AD⊥平面BCC1B1………………………………………………8分
又C1H平面BCC1B1
∴AD⊥C1H
且C1H⊥B1D ,
B1D∩AD= D
B1D、AD平面AB1D
∴C1H⊥平面AB1D………………………………………………………10分
∴线段C1H的长即为点C1到平面AB1D的距离
在△C1B1D中,C1B1=2, C1D=B1D=,
则由余弦定理,cos∠B1C1D==
∴sin∠B1C1D=
∴C1H===
∴点C1到平面AB1D的距离为………………………………………12分
法二:在正三棱柱ABC-A1B1C1中,
C1C⊥平面ABC,AD平面ABC,
∴C1C⊥ AD
在△ABC中,AB=AC, BD=CD,
∴AD⊥ BC
且BC∩C1C= C
BC、C1C平面BCC1B1
∴AD⊥平面BCC1B1…………………………………………………………8分
设点C1到平面AB1D的距离为h,
则由V=V
得S·h=S·AD …………………………………………………10分
在△AB1D中,AB1=2,B1D=,AD=,
则由余弦定理,cos∠AB1D==
∴sin∠AB1D=
∴S=false
又S=false
∴··h=·2·
∴h=
∴点C1到平面AB1D的距离为………………………………………12分
(不管是定义法还是等积法,均需先证线面垂直,否则扣2分)
(等积法若计算过程过于简洁,则酌情扣分)
22.(本小题满分12分)
(1)在等腰梯形ABCD中,AB=2, BC=DC=1,
则AC= ,
∴AC?+BC?=AB?
∴AC⊥BC………………………………………………………………………1分
又D1在底面ABCD上的射影恰为点C,
∴D1C⊥平面ABCD
且BC平面ABCD
∴D1C⊥BC………………………………………………………………………2分
且AC⊥BC
AC∩D1C=C
AC、D1C平面AD1C
∴BC⊥平面AD1C
且BC平面BCC1B1
∴平面AD1C⊥平面BCC1B1……………………………………………………4分
3072765160020
(2)过点D作DE⊥AC, 垂足为E,
过点E作EF⊥AD1, 垂足为F,
连接DF
∵D1C⊥平面ABCD,
DE平面ABCD,
∴D1C⊥DE
又DE⊥AC,
AC∩D1C= C
AC、D1C平面CAD1
∴DE⊥平面CAD1…………………………………6分
又AD1平面CAD1
∴DE⊥AD1
且EF⊥AD1,
DE∩EF=E
DE、EF平面DEF
∴AD1⊥平面DEF……………………………………………………………8分
又DF平面DEF
∴AD1⊥DF
且AD1⊥EF
∴∠DFE即为二面角C-AD1-D的平面角……………………………………9分
在△ADC中,AD=DC=1, AC=, DE⊥AC,
∴DE= ;
∵直线AD1与底面ABCD成30°角,
∴∠D1AC=30°
在Rt△EFA中,AE=,
∴EF=.
在Rt△DEF中,DE=,EF=,
∴DF=
∴cos∠DFE===
∴二面角C-AD1-D的余弦值为.……………………………………………………12分
(未证明两组线面垂直的,少一组扣2分;
未指出二面角的平面角,扣1分;
计算过程过于简洁,酌情扣分)
数 学
一?单项选择题:本大题共8小题,每小题5分,共计40分.在每小题给出的四个选项中,只有一项符合题目要求,请把答案填涂在答题卡相应位置.
1. 已知i为虚数单位,复数z满足z= ,则||=( )
A. B. C. D.
4084320457202. 某部门为了了解一批树苗的生长情况,在3000
棵树苗中随机抽取200棵,统计这200棵树苗
的高度,并绘制了频率分布直方图(如图),那么
根据该图可推测,在这3000棵树苗中高度小于
100cm的树苗棵数是( ).
A.360 B.600
C.840 D.1320
3. 已知m,n表示两条不同直线,α表示平面,下列说法正确的是( )
A.若m//α,n//α,则m//n B.若m⊥α,nα,则m⊥n
C.若m⊥α,m⊥n,则n//α D.若m//α,m⊥n,则n⊥α
4.已知在△ABC中,AB=2,AC=3,∠BAC=,点D为边BC上靠近B的三等分点,则·的值为( )
A.- B.- C. D.53390806485890(第5题)
(第5题)
410273520955055594257418070(第5题)
(第5题)
5.如图,棱锥D′-A′CD体积与长方体ABCD-A′B′C′D′体积的比值为( )53390806485890(第5题)
(第5题)
A. B. C. D.
6.若λsin160°+tan20°=,则实数λ的值为( )
A.3 B. C.2 D.4
49815756648457. 埃及胡夫金字塔是古代世界建筑奇迹之一,它的形状可视为一个正四棱锥,以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积,则其侧面三角形底边上的高与底面正方形的边长的比值为( )
A. B. C. D.
8.已知菱形ABCD边长为2,∠ABC=60?,沿对角线AC折叠成三棱锥B’-ACD,使得二面角
B'-AC-D为60°,设E为B’C的中点,F为三棱锥B'-ACD表面上的动点,且总满足AC⊥EF,则点F轨迹的长度为( )
A.2 B.3 C. D.
二?多项选择题:本大题共4小题,每小题5分,共计20分.在每小题给出的四个选项中,有多项符合题目要求,全部选对得5分,部分选对得2分,不选或有选错的得0分.请把答案填涂在答题卡相应位置.
9.下列命题中,真命题有 ( )
A.如果两个平面有三个不在一条直线上的公共点,那么这两个平面重合
B.两条直线可以确定一个平面
C.空间中,相交于同一点的三条直线在同一平面内
D.若M∈α,M∈β,α∩β=l,则M∈l
450088026860510.如图,在平面四边形ABCD中,已知∠B+∠D=180°,AB=2,
BC=4,CD=4,AD=2,下列四个结论中正确的是( )
A.∠B=∠D=90° B.四边形ABCD的面积为4+
C.AC=6 D.四边形ABCD的周长为6+4+2
11.z=1+cos2θ+isin2θ(-<θ<)(其中i为虚数单位)下列说法正确的是( )
A.复数z在复平面上对应的点可能落在第二象限 B.z可能为实数
C.|z|=2cosθ D.的实部为
12.如图所示,在正△ABC中,D,E分别为边AB,AC的中点,其中AB=8,将△ADE沿DE翻折至A'DE位置,使得二面角A'-DE-B为60°,则下列选项中正确的是( )
323088011430A.点A' 到平面BCED的距离为3
B.直线A'D与直线CE所成的角的余弦值为
C.A'D⊥BD
D. 四棱锥A' -BCED的外接球半径为
三?填空题:本题共4小题,每小题5分,共20分.其中第16题第一空3分,第二空2分.请把答案填写在答题卡相应位置.
13.一圆锥侧面展开图为半径为8的半圆,则此圆锥的体积为______.
14.某企业三月中旬生产A,B,C三种产品共3 000件,根据分层抽样的结果,企业统计员制作了如下的表格:
产品类别
A
B
C
产品数量(件)
1300
样本数量(件)
130
由于不小心,表格中A,C产品的有关数据已被污染看不清楚,统计员记的A产品的样本数
量比C产品的样本数量多10,根据以上信息,可得C产品的数量是________.
15.在△ABC中,已知AB=4,AC=3,P是边BC的垂直平分线上的一点,则·=
___________.
16.蹴鞠(如图所示),又名蹴球,蹴圆,筑圆,踢圆等,蹴有用脚蹴?踢?蹋的含义;鞠最早系
外包皮革?内实米糠的球.因而蹴鞠就是指古人以交蹴?蹋?踢皮球的活动,类似于今日的
足球.早在2006年5月,蹴鞠已作为非物质文化遗产经国务院批准列入第一批国家非物
质文化遗产名录.现已知某蹴鞠的表面上有四个点S?A?B?C,满足S-ABC是正三棱锥,
M3958590179705是SB的中点,CM⊥SA,侧棱长为2,则该蹴鞠的体积为__________;蹴鞠球心到平面
ABC的距离为____________.
四?解答题:本题共6小题,共70分.请在答题卡指定区域内作答,解答时应写出必要的文字说明,证明过程或演算步骤.
17.(本小题满分10分)
已知函数f(x)=2cos2+sinx.
(1)求函数f(x)在区间[0,π]上的单调增区间;
(2)当f(α)= ,且α∈(-, ) ,求sin(2α+) 的值.
18.(本小题满分12分)
3550285170180A
B
C
D
D1
A1
B1
C1
P
(第18题图)
A
B
C
D
D1
A1
B1
C1
P
(第18题图)
如图,在长方体ABCD-A1B1C1D1中,已知底面ABCD是正方形,点P是侧棱CC1上的一点.
(1)求证BD⊥A1P;
(2)若AC1//平面PBD,求的值.
19. (本小题满分12分)
如图,在矩形ABCD中,点E是BC边上中点,点F在边CD上.
4101465332740(1)若点F是CD上靠近C的三等分点.设=λ+μ ,求λ+μ的值;
(2)若AB=,BC=2,求· 的取值范围.
20.(本小题满分12分)
3768090208915在平面四边形ABCD中,∠ABC=,∠ADC=, BC=2.
(1)若△ABC面积为 ,求AC;
(2)若AD=2,∠ACB=∠ACD+ , 求tan∠ACD.
21.(本小题满分12分)
如图,正三棱柱ABC-A1B1C1的侧棱长和底面边长均为2,D是BC的中点.
406336520320求直线A1B与C1D所成角的余弦值;
求点C1到平面AB1D的距离.
22.(本小题满分12分)
如图,在四棱柱ABCD-A1B1C1D1中,底面ABCD是等腰梯形,AB=2,BC=DC=1,
AB∥CD,顶点D1在底面ABCD上的射影恰为点C.
(1)求证:平面AD1C⊥平面BCC1B1;
3455035158750(2)若直线AD1与底面ABCD成30°角,求二面角C-AD1-D的余弦值.
南京市第二十九中学2020-2021学年下高一6月学情检测2021.6
参考答案与评分标准
一、单项选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.D 2.B 3.B 4.D 5.C 6.D 7.C 8.D
二、多项选择题:本大题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求的.全部选对的得5分,部分选对的得2分,有选错的得0分.
9. AD 10.ACD 11.BCD 12.ABD
三、填空题:本大题共4小题,每小题5分,共20分.
13. 14.800 15.- 16.4π ,
四、解答题:本大题共6小题,共70分.
17.(本小题满分10分)
(1) f(x)=cosx+1+sinx=2sin(x+)+1 ……………………………………………1分
令-+2kπ≤x+≤+2kπ, k∈Z
得-+2kπ≤x≤+2kπ, k∈Z ……………………………………………3分
令k=0, 则-≤x≤, ……………………………………………4分
∴函数f(x)在区间[0,π]上的单调增区间为[0,] ………………………………5分
(2)由f(α)=,得2 sin(α+)+1= ,
∴sin(α+)= ………………………………………………………………7分
又∵α∈(-, ) , ∴-<α+<
∴cos(α+)=== ………………………………………9分
∴sin(2α+)=sin[2(α+)]=2sin(α+)cos(α+)=2··=. ………………10分
18.(本小题满分12分)
(1)连接A1C1.
因为ABCD-A1B1C1D1为长方体,所以侧棱C1C⊥平面ABCD.
又BD平面ABCD,所以CC1⊥BD. ……………………………………………2分
因为底面ABCD是正方形,所以AC⊥BD.
又AC∩CC1=C,AC面ACC1A1,CC1面ACC1A1,
所以BD⊥面ACC1A1. …………………………………………………4分
又因为A1P面ACC1A1,所以BD⊥A1P. …………………………………………6分
(2)连接AC交BD于点O,连接OP.
因为AC1//平面PBD,AC1平面ACC1,
3774440-567055O
A
B
C
D
D1
A1
B1
C1
P
(第18题图)
O
A
B
C
D
D1
A1
B1
C1
P
(第18题图)
平面ACC1∩平面BDP=OP,
所以AC1//OP. ………………………9分
因为四边形ABCD是正方形,对角线AC交BD于点O,
所以点O是AC的中点,所以AO=OC,
所以在△ACC1中,==1. …………12分
19.(本小题满分12分)
(1) ∵=-=-+,……………………………………………2分
又=λ+μ ,
且,不共线 ,
∴λ=-,μ= , ……………………………………………………………4分
∴λ+μ=-+= . …………………………………………………………5分
(不交代 , 不共线扣1分)
(2)以A为原点,以AB、AD所在直线为x轴、y轴,建立如图所示的平面直角坐标系,
∵AB=,BC=2,
∴B( , 0) , D(0 , 2) , C ( , 2) , E( , 1) ;
设F(x , 2) , x∈[0, ],
则=(x,2),=(x-,1) ,
∴·=x2-x+2=(x-)2+ , x∈[0, ] ;……………………………9分
当x=时,·的最小值为;
当x=0或时,·的最大值为2;
∴·的取值范围为[ , 2] . ……………………………………………………12分
20.(本小题满分12分)
(1)在△ABC中,∠ABC= , BC=2 ,
∴SΔABC=AB·BC·sin∠BAC= ,
∴AB=3; …………………………………………………………………………2分
在△ABC中,由余弦定理得,
AC2=AB2+BC2-2AB·BC·cos∠ABC=9+4-2×3×2×=7,
∴AC= . …………………………………………………………………………5分
(至少出现一次“在△ABC”中,否则扣1分)
(使用余弦定理时,必须先默公式,再代数值,最后得结果,否则扣1分)
3961765187960(2)设∠ACD=α , 则∠ACB=α+ ;
在Rt△ACD中,AD=2,
∴AC==, ……………………………………7分
在△ABC中,∠BAC=π-∠ACB-ABC=-α ,
由正弦定理得,=
∴= ; ………………………………………………………9分
∴2sinα=cosα , ∴tanα=
∴tan∠ACD=…………………………………………………………………12分
21.(本小题满分12分)
(1)法一:连接A1C, 交AC1于点E,连接DE.
在三棱柱ABC-A1B1C1中,四边形ACC1A1为平行四边形,
4082415-78740 ∴E是A1C的中点……………………………………2分
在△A1BC中,D、E分别是BC、A1C的中点,
∴DE∥A1B…………………………………………………4分
∴∠EDC1(或其补角)即为直线A1B和C1D所成的角
在△EDC1中, ED=, DC1= , C1E= ,
由余弦定理,cos∠EDC1==
∴直线A1B和C1D所成的角的余弦值为.………………………………6分
法二:取B1C1的中点F,连接BF、A1F
4034790188595在三棱柱ABC-A1B1C1中,BC B1C1
∵D、F分别是BC、 B1C1的中点,
∴BDFC1……………………………………………………2分
∴四边形BDC1F为平行四边形
∴BF∥DC1……………………………………………………4分
∴∠FBA1(或其补角)即为直线A1B和C1D所成的角
在△FBA1中,BA1=2, BF=, A1F=,
由余弦定理,cos∠FBA1= = .
∴直线A1B和C1D所成的角的余弦值为.………………………………6分
法三:将正三棱柱ABC-A1B1C1补成如图所示的直平行六面体ABGC- A1B1G1C1
连接C1G、DG
3853815136525 则A1B∥C1G…………………………………4分
∴∠DC1G(或其补角)即为直线A1B和C1D所成的角
在△DC1G中,DC1=, C1G=2,DG=,
由余弦定理,cos∠DC1G= = .
∴直线A1B和C1D所成的角的余弦值为.………………6分
(未指出“………即为直线A1B和DC1所成的角”扣1分)
3777615-43180(2) 法一:过C1作C1H⊥B1D, 垂足为H
在正三棱柱ABC-A1B1C1中,
C1C⊥平面ABC,AD平面ABC,
∴C1C⊥ AD
在△ABC中,AB=AC, BD=CD,
∴AD⊥ BC
且BC∩C1C= C
BC、C1C平面BCC1B1
∴AD⊥平面BCC1B1………………………………………………8分
又C1H平面BCC1B1
∴AD⊥C1H
且C1H⊥B1D ,
B1D∩AD= D
B1D、AD平面AB1D
∴C1H⊥平面AB1D………………………………………………………10分
∴线段C1H的长即为点C1到平面AB1D的距离
在△C1B1D中,C1B1=2, C1D=B1D=,
则由余弦定理,cos∠B1C1D==
∴sin∠B1C1D=
∴C1H===
∴点C1到平面AB1D的距离为………………………………………12分
法二:在正三棱柱ABC-A1B1C1中,
C1C⊥平面ABC,AD平面ABC,
∴C1C⊥ AD
在△ABC中,AB=AC, BD=CD,
∴AD⊥ BC
且BC∩C1C= C
BC、C1C平面BCC1B1
∴AD⊥平面BCC1B1…………………………………………………………8分
设点C1到平面AB1D的距离为h,
则由V=V
得S·h=S·AD …………………………………………………10分
在△AB1D中,AB1=2,B1D=,AD=,
则由余弦定理,cos∠AB1D==
∴sin∠AB1D=
∴S=false
又S=false
∴··h=·2·
∴h=
∴点C1到平面AB1D的距离为………………………………………12分
(不管是定义法还是等积法,均需先证线面垂直,否则扣2分)
(等积法若计算过程过于简洁,则酌情扣分)
22.(本小题满分12分)
(1)在等腰梯形ABCD中,AB=2, BC=DC=1,
则AC= ,
∴AC?+BC?=AB?
∴AC⊥BC………………………………………………………………………1分
又D1在底面ABCD上的射影恰为点C,
∴D1C⊥平面ABCD
且BC平面ABCD
∴D1C⊥BC………………………………………………………………………2分
且AC⊥BC
AC∩D1C=C
AC、D1C平面AD1C
∴BC⊥平面AD1C
且BC平面BCC1B1
∴平面AD1C⊥平面BCC1B1……………………………………………………4分
3072765160020
(2)过点D作DE⊥AC, 垂足为E,
过点E作EF⊥AD1, 垂足为F,
连接DF
∵D1C⊥平面ABCD,
DE平面ABCD,
∴D1C⊥DE
又DE⊥AC,
AC∩D1C= C
AC、D1C平面CAD1
∴DE⊥平面CAD1…………………………………6分
又AD1平面CAD1
∴DE⊥AD1
且EF⊥AD1,
DE∩EF=E
DE、EF平面DEF
∴AD1⊥平面DEF……………………………………………………………8分
又DF平面DEF
∴AD1⊥DF
且AD1⊥EF
∴∠DFE即为二面角C-AD1-D的平面角……………………………………9分
在△ADC中,AD=DC=1, AC=, DE⊥AC,
∴DE= ;
∵直线AD1与底面ABCD成30°角,
∴∠D1AC=30°
在Rt△EFA中,AE=,
∴EF=.
在Rt△DEF中,DE=,EF=,
∴DF=
∴cos∠DFE===
∴二面角C-AD1-D的余弦值为.……………………………………………………12分
(未证明两组线面垂直的,少一组扣2分;
未指出二面角的平面角,扣1分;
计算过程过于简洁,酌情扣分)
同课章节目录
