人教版2021年八年级数学上册11.3多边形及其内角和 同步练习 (word版,含答案)
文档属性
| 名称 | 人教版2021年八年级数学上册11.3多边形及其内角和 同步练习 (word版,含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 225.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-01 17:46:50 | ||
图片预览


文档简介
人教版2021年八年级数学上册11.3多边形及其内角和 同步练习
一、选择题
1.下列图中不是凸多边形的是( )
A. B. C. D.
2.下列说法中,正确的有( )
①由几条线段连接起来组成的图形叫多边形;
②三角形是边数最少的多边形;
③n边形有n条边、n个顶点.
A.0个 B.1个 C.2个 D.3个
3.在四边形ABCD中,如果∠A+∠B+∠C=260°,那么∠D的度数为( )
A.120° B.110° C.100° D.90°
4.六边形共有几条对角线( )
A.6 B.7 C.8 D.9
5.如图所示,小华从A点出发,沿直线前进10米后左转false,再沿直线前进10米,又向左转false,false,照这样走下去,他第一次回到出发地A点时,一共走的路程是( )
A.200米 B.180米 C.160米 D.140米
6.已知一个多边形的内角和与外角和的比是9:2,则这个多边形的边数是false false
A.9 B.10 C.11 D.12
7.若从false边形的一个顶点出发,最多可以作3条对角线,则该false边形的内角和是( )
A.false B.false C.false D.false
8.过某个多边形一点顶点的所有对角线,将这个多边形分成了5个三角形,则这个多边形是( )
A.五边形 B.六边形 C.七边形 D.八边形
9.一个多边形的边数由原来的3增加到n时(n>3,且n为正整数),它的外角和( )
A.增加(n﹣2)×180° B.减小(n﹣2)×180°
C.增加(n﹣1)×180° D.没有改变
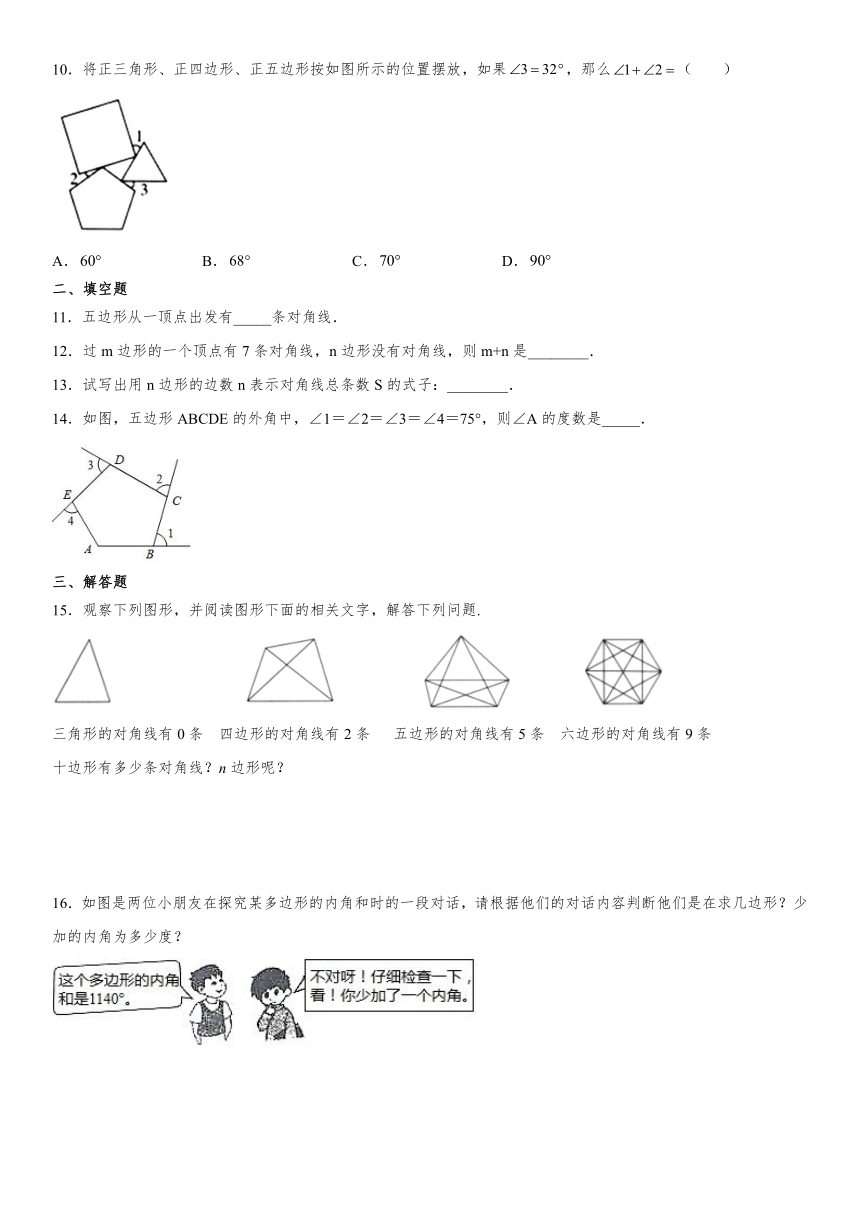
10.将正三角形、正四边形、正五边形按如图所示的位置摆放,如果false,那么false( )
A.false B.false C.false D.false
二、填空题
11.五边形从一顶点出发有_____条对角线.
12.过m边形的一个顶点有7条对角线,n边形没有对角线,则m+n是________.
13.试写出用n边形的边数n表示对角线总条数S的式子:________.
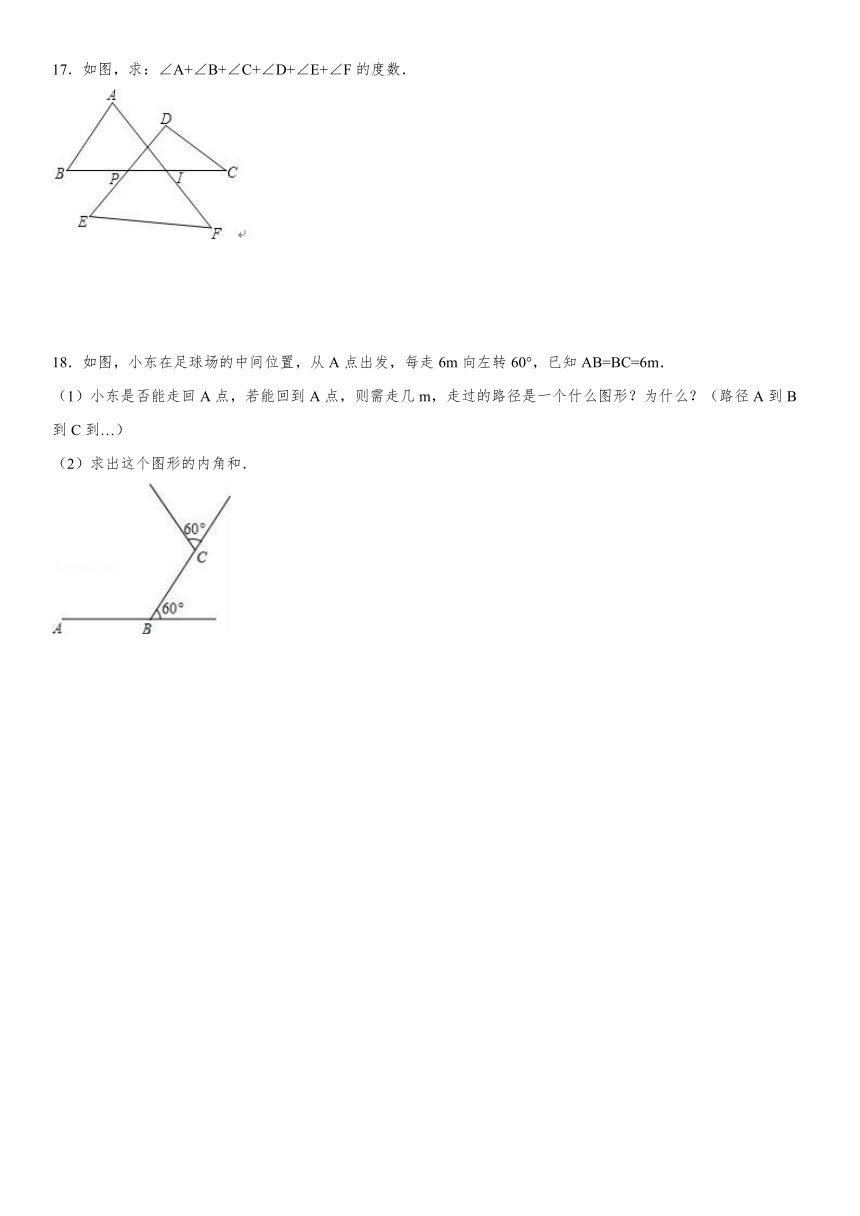
14.如图,五边形ABCDE的外角中,∠1=∠2=∠3=∠4=75°,则∠A的度数是_____.
三、解答题
15.观察下列图形,并阅读图形下面的相关文字,解答下列问题.
三角形的对角线有0条 四边形的对角线有2条 五边形的对角线有5条 六边形的对角线有9条
十边形有多少条对角线?n边形呢?
16.如图是两位小朋友在探究某多边形的内角和时的一段对话,请根据他们的对话内容判断他们是在求几边形?少加的内角为多少度?
17.如图,求:∠A+∠B+∠C+∠D+∠E+∠F的度数.
18.如图,小东在足球场的中间位置,从A点出发,每走6m向左转60°,已知AB=BC=6m.
(1)小东是否能走回A点,若能回到A点,则需走几m,走过的路径是一个什么图形?为什么?(路径A到B到C到…)
(2)求出这个图形的内角和.
参考答案
1.A
【详解】
根据凸多边形的概念,如果多边形的边都在任何一条边所在的直线的同旁,该多边形即是凸多边形.否则即是凹多边形,故A不是凸多边形;B是凸多边形;C是凸多边形;D是凸多边形.
故选A.
2.C
【分析】
根据多边形的定义判断即可.
【详解】
由一些线段首尾顺次相接组成的封闭图形叫做多边形,①不正确;易知②③正确,
故选:C.
【点睛】
本题考查了多边形的定义,掌握知识点是解题关键.
3.C
【分析】
利用四边形的内角和减去其它角的度数即可求解.
【详解】
∵在四边形ABCD中,∠A+∠B+∠C+∠D=360°,且∠A+∠B+∠C=260°,
∴∠D=100°,
故选C
4.D
【详解】
根据题意得:false=9,
则六边形共有9条对角线,
故选D
5.B
【分析】
多边形的外角和为360°每一个外角都为20°,依此可求边数,再求多边形的周长.
【详解】
∵多边形的外角和为360°,而每一个外角为20°,
∴多边形的边数为360°÷20°=18,
∴小华一共走了:18×10=180米.
故选B.
【点睛】
本题考查了多边形的外角与内角,利用多边形外角和除以一个外角得出多边形的边数是解题的关键.
6.C
【分析】
根据多边形的内角和公式,多边形的外角和,可得方程,解方程,即可得答案.
【详解】
设这个多边形的边数是n,由题意得
(n-2)×180°:360°=9:2.
解得n=11,
故选C.
【点睛】
本题考查了多边形的内角与外角,利用了多边形的内角和公式:(n-2)180°,外角和是360.
7.B
【解析】
【分析】
根据n边形从一个顶点出发可引出(n-3)条对角线,可得n-3=3,求出n的值,最后根据多边形内角和公式可得结论.
【详解】
由题意得:n-3=3,解得n=6,
则该n边形的内角和是:(6-2)×180°=720°,
故选B.
【点睛】
本题考查了多边形的对角线和多边形的内角和公式,熟记n边形从一个顶点出发可引出(n-3)条对角线是解答此题的关键.
8.C
【分析】
一个四边形如此操作可得2个三角形;一个五边形如此操作可得3个三角形;一个六边形如此操作可得3个三角形,据此可得规律,如此操作后,得到的三角形数量比其边数少2.
【详解】
解:由规律可知,如此操作后得到的三角形数量比该多边形的边数少2,则该多边形的边数为5+2=7,为七边形,
故选择C.
【点睛】
本题考查了几何图形中的找规律.
9.D
【分析】
根据多边形的外角和等于360°,与边数无关即可解答.
【详解】
∵多边形的外角和等于360°,与边数无关,
∴一个多边形的边数由3增加到n时,其外角度数的和还是360°,保持不变.
故选D.
【点睛】
本题考查了多边形的外角和,熟知多边形的外角和等于360°是解题的关键.
10.C
【分析】
根据平角的定义分别用∠1,∠2,∠3表示阴影部分三角形的三个外角,然后根据三角形的外角和是360°列式即可得到答案.
【详解】
解:如图所示,正三角形、正四边形、正五边形的每个内角的度数分别为false,
∴中间阴影部分的三角形的三个外角的度数分别为false,
∵三角形的外角和为false,
∴false.
false,
故选C.
【点睛】
本题考查的是三角形外角和定理,熟知正三角形、正四边形、正五边形各内角的度数是解答此题的关键.
11.2
【解析】
根据n边形从一个顶点出发可引出(n-3)条对角线可直接得到
从五边形的一个顶点可以引:5?3=2条对角线,
故答案为2.
12.13
【解析】
∵过m边形的一个顶点有7条对角线,n边形没有对角线,
∴m?3=7,n=3,
∴m=10,n=3,
∴m+n=10+3=13,
故答案为13.
13.S=falsen(n﹣3)
【解析】
用n边形的边数n表示对角线总条数S的式子:S=falsen(n?3);
故答案为S=falsen(n?3).
14.120°.
【分析】
根据多边形的外角和求出与∠A相邻的外角的度数,然后根据邻补角的和等于180°列式求解即可.
【详解】
∵∠1=∠2=∠3=∠4=75°,
∴与∠A相邻的外角=360°﹣75°×4=360°﹣300°=60°,
∴∠A=180°﹣60°=120°.
故答案为120°.
【点睛】
本题主要考查了多边形外角和定理,熟练掌握相关概念是解题关键.
15.35;false
【分析】
根据已知条件找出对角线条数与边数的关系,即可得到结论;
【详解】
四边形的对角线条数为false,
五边形的对角线条数为false,
六边形的对角线条数为false,
∴十边形的对角线条数为false,
n边形的对角线条数为false.
【点睛】
本题主要考查了多边形对角线知识点,准确判断是解题的关键.
16.他们在求九边形的内角和;少加的那个内角为120度.
【分析】
根据n边形的内角和公式,则内角和应是180°的倍数,且每一个内角应大于0°而小于180度,根据这些条件进行分析求解即可.
【详解】
解:1140°÷180°=6…60°,
则边数是:6+1+2=9;
他们在求九边形的内角和;
180°﹣60°=120°,
少加的那个内角为120度.
【点睛】
本题主要考查多边形内角和公式的灵活运用,解题的关键是找到相应度数的等量关系.注意多边形的一个内角一定大于0°,并且小于180度.
17.证明见解析
【解析】
分析:根据三角形外角的性质及四边形的内角和为360°,即可解答.
本题解析:
如图,
?
∵∠BPO是△PDC的外角,
∴∠BPO=∠C+∠D,
∵∠POA是△OEF的外角,
∴∠POA=∠E+∠F,
∵∠A+∠B+∠BPO+∠POA=360°,
18.(1)走过的路径是一个边长为6的正六边形;(2)720°.
【详解】
试题分析:1)利用外角和为360°计算出多边形的边数即可;
(2)利用内角和公式直接计算即可.
试题解析:(1)false从A点出发,每走6m向左转60°,
false
false走过的路径是一个边长为6的正六边形;
(2)正六边形的内角和为:(6﹣2)×180°=720°.
一、选择题
1.下列图中不是凸多边形的是( )
A. B. C. D.
2.下列说法中,正确的有( )
①由几条线段连接起来组成的图形叫多边形;
②三角形是边数最少的多边形;
③n边形有n条边、n个顶点.
A.0个 B.1个 C.2个 D.3个
3.在四边形ABCD中,如果∠A+∠B+∠C=260°,那么∠D的度数为( )
A.120° B.110° C.100° D.90°
4.六边形共有几条对角线( )
A.6 B.7 C.8 D.9
5.如图所示,小华从A点出发,沿直线前进10米后左转false,再沿直线前进10米,又向左转false,false,照这样走下去,他第一次回到出发地A点时,一共走的路程是( )
A.200米 B.180米 C.160米 D.140米
6.已知一个多边形的内角和与外角和的比是9:2,则这个多边形的边数是false false
A.9 B.10 C.11 D.12
7.若从false边形的一个顶点出发,最多可以作3条对角线,则该false边形的内角和是( )
A.false B.false C.false D.false
8.过某个多边形一点顶点的所有对角线,将这个多边形分成了5个三角形,则这个多边形是( )
A.五边形 B.六边形 C.七边形 D.八边形
9.一个多边形的边数由原来的3增加到n时(n>3,且n为正整数),它的外角和( )
A.增加(n﹣2)×180° B.减小(n﹣2)×180°
C.增加(n﹣1)×180° D.没有改变
10.将正三角形、正四边形、正五边形按如图所示的位置摆放,如果false,那么false( )
A.false B.false C.false D.false
二、填空题
11.五边形从一顶点出发有_____条对角线.
12.过m边形的一个顶点有7条对角线,n边形没有对角线,则m+n是________.
13.试写出用n边形的边数n表示对角线总条数S的式子:________.
14.如图,五边形ABCDE的外角中,∠1=∠2=∠3=∠4=75°,则∠A的度数是_____.
三、解答题
15.观察下列图形,并阅读图形下面的相关文字,解答下列问题.
三角形的对角线有0条 四边形的对角线有2条 五边形的对角线有5条 六边形的对角线有9条
十边形有多少条对角线?n边形呢?
16.如图是两位小朋友在探究某多边形的内角和时的一段对话,请根据他们的对话内容判断他们是在求几边形?少加的内角为多少度?
17.如图,求:∠A+∠B+∠C+∠D+∠E+∠F的度数.
18.如图,小东在足球场的中间位置,从A点出发,每走6m向左转60°,已知AB=BC=6m.
(1)小东是否能走回A点,若能回到A点,则需走几m,走过的路径是一个什么图形?为什么?(路径A到B到C到…)
(2)求出这个图形的内角和.
参考答案
1.A
【详解】
根据凸多边形的概念,如果多边形的边都在任何一条边所在的直线的同旁,该多边形即是凸多边形.否则即是凹多边形,故A不是凸多边形;B是凸多边形;C是凸多边形;D是凸多边形.
故选A.
2.C
【分析】
根据多边形的定义判断即可.
【详解】
由一些线段首尾顺次相接组成的封闭图形叫做多边形,①不正确;易知②③正确,
故选:C.
【点睛】
本题考查了多边形的定义,掌握知识点是解题关键.
3.C
【分析】
利用四边形的内角和减去其它角的度数即可求解.
【详解】
∵在四边形ABCD中,∠A+∠B+∠C+∠D=360°,且∠A+∠B+∠C=260°,
∴∠D=100°,
故选C
4.D
【详解】
根据题意得:false=9,
则六边形共有9条对角线,
故选D
5.B
【分析】
多边形的外角和为360°每一个外角都为20°,依此可求边数,再求多边形的周长.
【详解】
∵多边形的外角和为360°,而每一个外角为20°,
∴多边形的边数为360°÷20°=18,
∴小华一共走了:18×10=180米.
故选B.
【点睛】
本题考查了多边形的外角与内角,利用多边形外角和除以一个外角得出多边形的边数是解题的关键.
6.C
【分析】
根据多边形的内角和公式,多边形的外角和,可得方程,解方程,即可得答案.
【详解】
设这个多边形的边数是n,由题意得
(n-2)×180°:360°=9:2.
解得n=11,
故选C.
【点睛】
本题考查了多边形的内角与外角,利用了多边形的内角和公式:(n-2)180°,外角和是360.
7.B
【解析】
【分析】
根据n边形从一个顶点出发可引出(n-3)条对角线,可得n-3=3,求出n的值,最后根据多边形内角和公式可得结论.
【详解】
由题意得:n-3=3,解得n=6,
则该n边形的内角和是:(6-2)×180°=720°,
故选B.
【点睛】
本题考查了多边形的对角线和多边形的内角和公式,熟记n边形从一个顶点出发可引出(n-3)条对角线是解答此题的关键.
8.C
【分析】
一个四边形如此操作可得2个三角形;一个五边形如此操作可得3个三角形;一个六边形如此操作可得3个三角形,据此可得规律,如此操作后,得到的三角形数量比其边数少2.
【详解】
解:由规律可知,如此操作后得到的三角形数量比该多边形的边数少2,则该多边形的边数为5+2=7,为七边形,
故选择C.
【点睛】
本题考查了几何图形中的找规律.
9.D
【分析】
根据多边形的外角和等于360°,与边数无关即可解答.
【详解】
∵多边形的外角和等于360°,与边数无关,
∴一个多边形的边数由3增加到n时,其外角度数的和还是360°,保持不变.
故选D.
【点睛】
本题考查了多边形的外角和,熟知多边形的外角和等于360°是解题的关键.
10.C
【分析】
根据平角的定义分别用∠1,∠2,∠3表示阴影部分三角形的三个外角,然后根据三角形的外角和是360°列式即可得到答案.
【详解】
解:如图所示,正三角形、正四边形、正五边形的每个内角的度数分别为false,
∴中间阴影部分的三角形的三个外角的度数分别为false,
∵三角形的外角和为false,
∴false.
false,
故选C.
【点睛】
本题考查的是三角形外角和定理,熟知正三角形、正四边形、正五边形各内角的度数是解答此题的关键.
11.2
【解析】
根据n边形从一个顶点出发可引出(n-3)条对角线可直接得到
从五边形的一个顶点可以引:5?3=2条对角线,
故答案为2.
12.13
【解析】
∵过m边形的一个顶点有7条对角线,n边形没有对角线,
∴m?3=7,n=3,
∴m=10,n=3,
∴m+n=10+3=13,
故答案为13.
13.S=falsen(n﹣3)
【解析】
用n边形的边数n表示对角线总条数S的式子:S=falsen(n?3);
故答案为S=falsen(n?3).
14.120°.
【分析】
根据多边形的外角和求出与∠A相邻的外角的度数,然后根据邻补角的和等于180°列式求解即可.
【详解】
∵∠1=∠2=∠3=∠4=75°,
∴与∠A相邻的外角=360°﹣75°×4=360°﹣300°=60°,
∴∠A=180°﹣60°=120°.
故答案为120°.
【点睛】
本题主要考查了多边形外角和定理,熟练掌握相关概念是解题关键.
15.35;false
【分析】
根据已知条件找出对角线条数与边数的关系,即可得到结论;
【详解】
四边形的对角线条数为false,
五边形的对角线条数为false,
六边形的对角线条数为false,
∴十边形的对角线条数为false,
n边形的对角线条数为false.
【点睛】
本题主要考查了多边形对角线知识点,准确判断是解题的关键.
16.他们在求九边形的内角和;少加的那个内角为120度.
【分析】
根据n边形的内角和公式,则内角和应是180°的倍数,且每一个内角应大于0°而小于180度,根据这些条件进行分析求解即可.
【详解】
解:1140°÷180°=6…60°,
则边数是:6+1+2=9;
他们在求九边形的内角和;
180°﹣60°=120°,
少加的那个内角为120度.
【点睛】
本题主要考查多边形内角和公式的灵活运用,解题的关键是找到相应度数的等量关系.注意多边形的一个内角一定大于0°,并且小于180度.
17.证明见解析
【解析】
分析:根据三角形外角的性质及四边形的内角和为360°,即可解答.
本题解析:
如图,
?
∵∠BPO是△PDC的外角,
∴∠BPO=∠C+∠D,
∵∠POA是△OEF的外角,
∴∠POA=∠E+∠F,
∵∠A+∠B+∠BPO+∠POA=360°,
18.(1)走过的路径是一个边长为6的正六边形;(2)720°.
【详解】
试题分析:1)利用外角和为360°计算出多边形的边数即可;
(2)利用内角和公式直接计算即可.
试题解析:(1)false从A点出发,每走6m向左转60°,
false
false走过的路径是一个边长为6的正六边形;
(2)正六边形的内角和为:(6﹣2)×180°=720°.
