人教五年级上册数学课件-《组合图形的面积》(共31张ppt)
文档属性
| 名称 | 人教五年级上册数学课件-《组合图形的面积》(共31张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-31 17:23:32 | ||
图片预览




文档简介
(共31张PPT)
组合图形面积的计算
人教版
数学
五年级
上册
课堂导入
课堂小结
课堂练习
新知探究
课堂作业
第6单元·多边形的面积
1.结合生活实际认识组合图形,并掌握用分解法或添补法求组合图形的面积。
?
????
2.根据各种组合图形的自身条件,选择有效的计算方法进行面积计算。
?
????
3.能运用组合图形的知识,解决生活中组合图形的实际问题。
学习目标
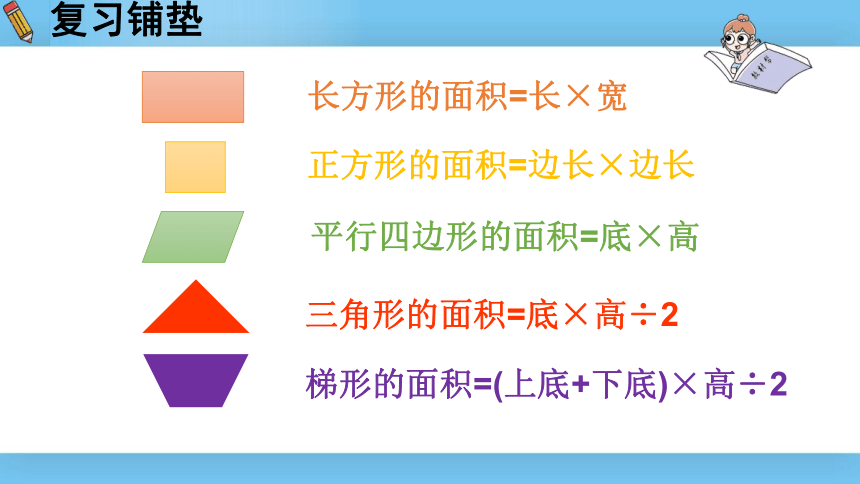
梯形的面积=(上底+下底)×高÷2
长方形的面积=长×宽
正方形的面积=边长×边长
三角形的面积=底×高÷2
平行四边形的面积=底×高
复习铺垫
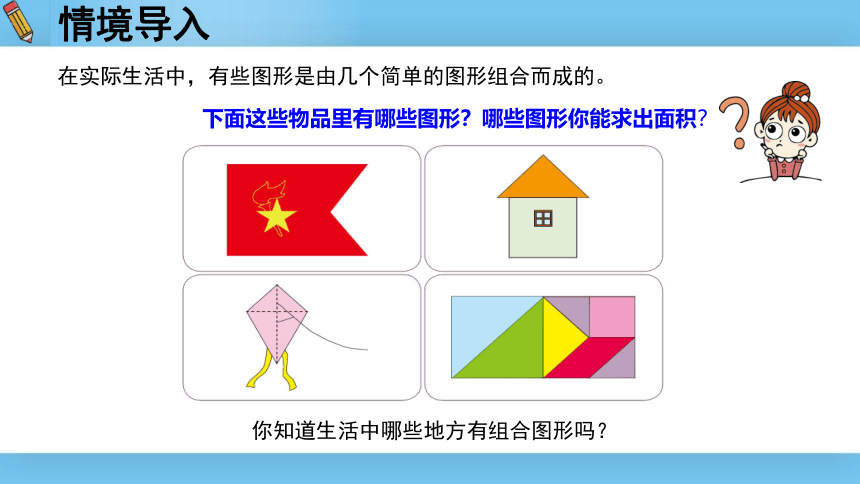
在实际生活中,有些图形是由几个简单的图形组合而成的。
下面这些物品里有哪些图形?哪些图形你能求出面积?
你知道生活中哪些地方有组合图形吗?
情境导入
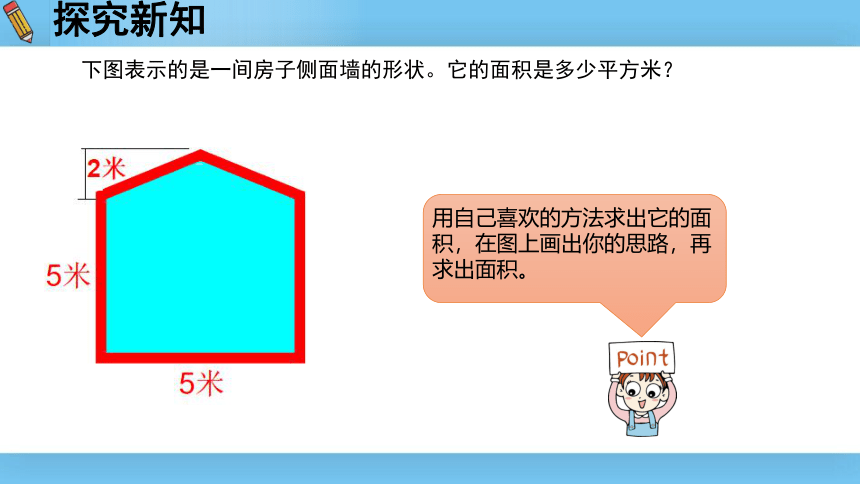
下图表示的是一间房子侧面墙的形状。它的面积是多少平方米?
探究新知
用自己喜欢的方法求出它的面积,在图上画出你的思路,再求出面积。
5米
2米
5米
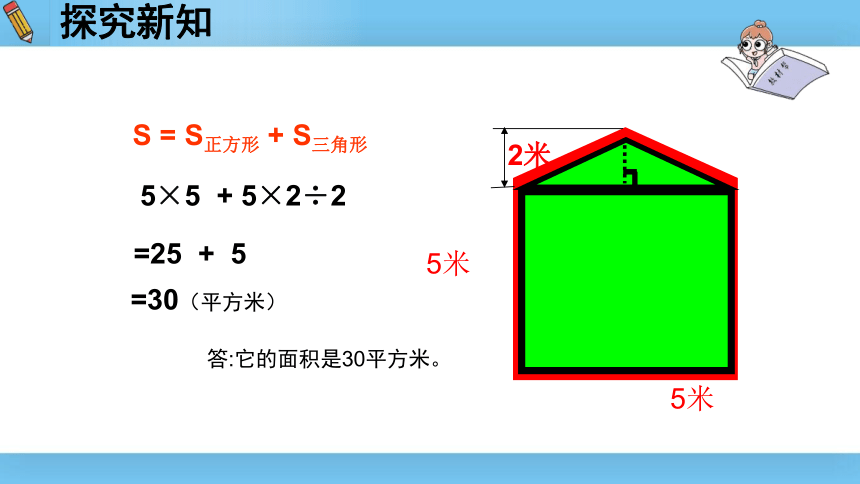
S
=
S正方形
+
S三角形
5×5
+
5×2÷2
=25
+
5
=30(平方米)
答:它的面积是30平方米。
探究新知
5米
5米
2米
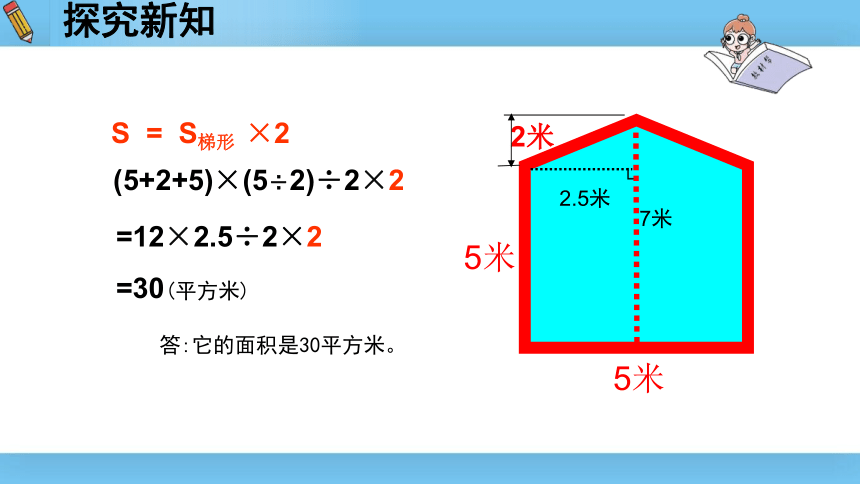
答:它的面积是30平方米。
S
=
S梯形
×2
(5+2+5)×(5÷2)÷2×2
=12×2.5÷2×2
=30(平方米)
探究新知
2.5米
7米
5米
5米
2米
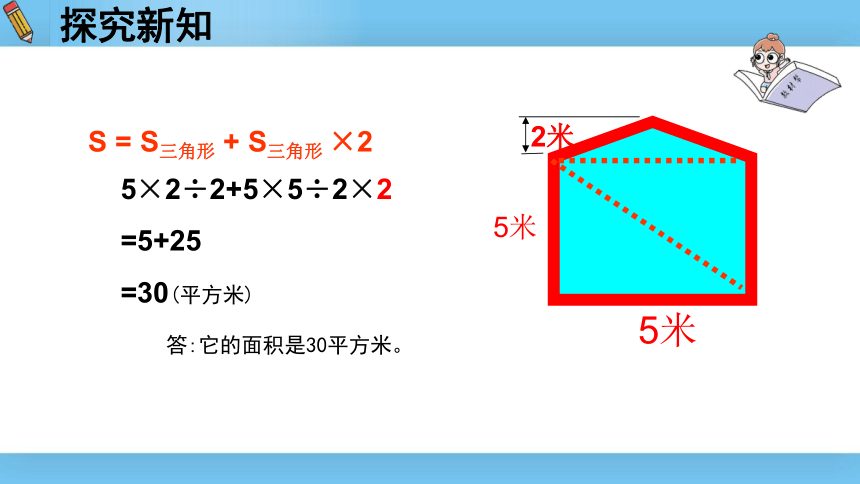
答:它的面积是30平方米。
5×2÷2+5×5÷2×2
=5+25
=30(平方米)
探究新知
S
=
S三角形
+
S三角形
×2
5米
5
米
2米
答:它的面积是30平方米。
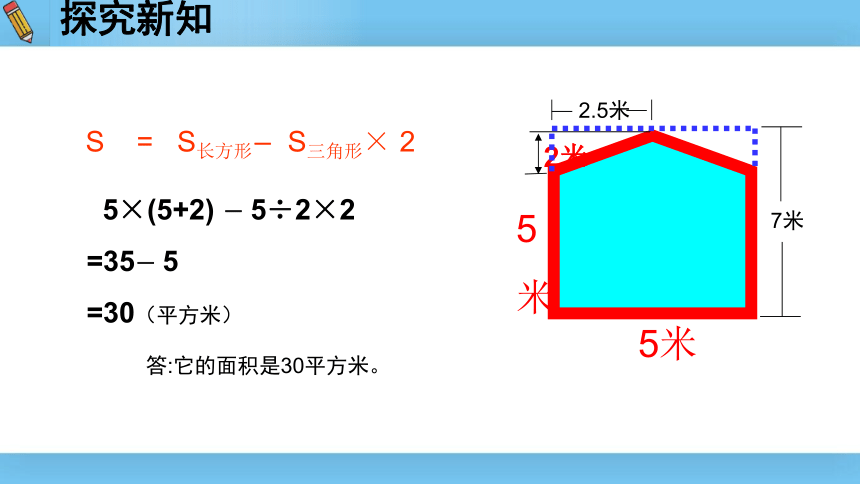
5×(5+2)
-
5÷2×2
=35-
5
=30(平方米)
S
=
S长方形-
S三角形×
2
探究新知
2.5米
7米
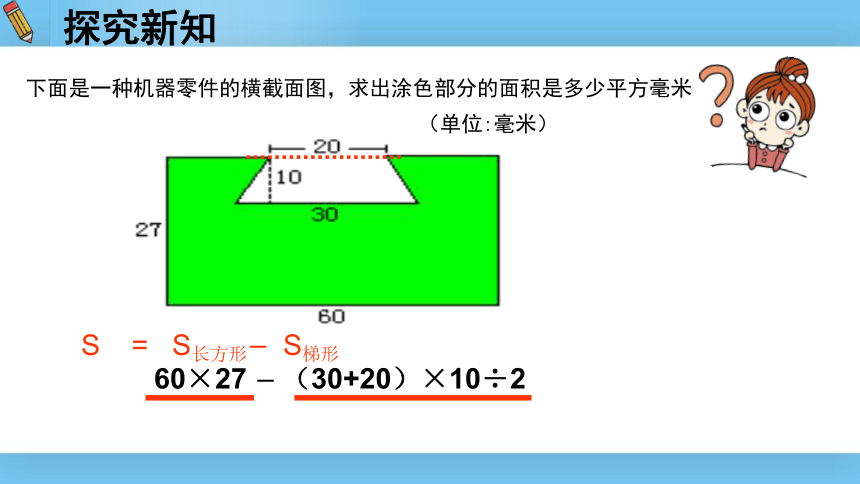
下面是一种机器零件的横截面图,求出涂色部分的面积是多少平方毫米
60×27
-
(30+20)×10÷2
(单位:毫米)
探究新知
S
=
S长方形-
S梯形
探究新知
要计算下图的面积,你认为哪种方法是对的?为什么?(单位:厘米)
10
8
4
5
①10×8-5×4
②8×5+5×4
③(8+4)×5÷2+(10+5)×4÷2
探究新知
10
8
4
5
①10×8-5×4
探究新知
10
8
4
5
②8×5+5×4
5
探究新知
10
8
4
5
③(8+4)×5÷2+(10+5)×4÷2
4
5
探究新知
这是我们少先队的中队旗,怎样算出它的面积。(你能想出不同的方法吗?)
课堂练习
思考题:计算下面图形的面积,你能想出不同的解法吗
(单位:米)
6
5
12
10
(10+5)×6÷2+6×5
S
=
S梯形
+
S长方形
课堂练习
6
5
12
10
5×6÷2+12×5
S
=
S三角形
+
S长方形
6
5
12
10
12×10÷2
+
5×6÷2
S
=
S大三角形
+
S小三角形
6
5
12
10
12×10
-(12+6)×5÷2
S
=
S长方形
-
S梯形
6
5
12
10
6×10
÷2+(12+6)×5÷2
S
=
S三角形
+
S梯形
求组合图形的基本步骤和方法:
(1)观察、分析这个组合图形可以分割成哪些能计算面积的基本图形。
(2)找出计算基本图形面积的条件。
(3)先计算出基本图形的面积,再计算出组合图形的面积。
课堂小结
同学们,组合图形在我们日常生活应用广泛,好好学习吧,发挥你们的智慧和创造力,为美化我们的校园和家园出一份力,让我们生活的环境更加美丽可爱!
组合图形面积的计算
人教版
数学
五年级
上册
课堂导入
课堂小结
课堂练习
新知探究
课堂作业
第6单元·多边形的面积
1.结合生活实际认识组合图形,并掌握用分解法或添补法求组合图形的面积。
?
????
2.根据各种组合图形的自身条件,选择有效的计算方法进行面积计算。
?
????
3.能运用组合图形的知识,解决生活中组合图形的实际问题。
学习目标
梯形的面积=(上底+下底)×高÷2
长方形的面积=长×宽
正方形的面积=边长×边长
三角形的面积=底×高÷2
平行四边形的面积=底×高
复习铺垫
在实际生活中,有些图形是由几个简单的图形组合而成的。
下面这些物品里有哪些图形?哪些图形你能求出面积?
你知道生活中哪些地方有组合图形吗?
情境导入
下图表示的是一间房子侧面墙的形状。它的面积是多少平方米?
探究新知
用自己喜欢的方法求出它的面积,在图上画出你的思路,再求出面积。
5米
2米
5米
S
=
S正方形
+
S三角形
5×5
+
5×2÷2
=25
+
5
=30(平方米)
答:它的面积是30平方米。
探究新知
5米
5米
2米
答:它的面积是30平方米。
S
=
S梯形
×2
(5+2+5)×(5÷2)÷2×2
=12×2.5÷2×2
=30(平方米)
探究新知
2.5米
7米
5米
5米
2米
答:它的面积是30平方米。
5×2÷2+5×5÷2×2
=5+25
=30(平方米)
探究新知
S
=
S三角形
+
S三角形
×2
5米
5
米
2米
答:它的面积是30平方米。
5×(5+2)
-
5÷2×2
=35-
5
=30(平方米)
S
=
S长方形-
S三角形×
2
探究新知
2.5米
7米
下面是一种机器零件的横截面图,求出涂色部分的面积是多少平方毫米
60×27
-
(30+20)×10÷2
(单位:毫米)
探究新知
S
=
S长方形-
S梯形
探究新知
要计算下图的面积,你认为哪种方法是对的?为什么?(单位:厘米)
10
8
4
5
①10×8-5×4
②8×5+5×4
③(8+4)×5÷2+(10+5)×4÷2
探究新知
10
8
4
5
①10×8-5×4
探究新知
10
8
4
5
②8×5+5×4
5
探究新知
10
8
4
5
③(8+4)×5÷2+(10+5)×4÷2
4
5
探究新知
这是我们少先队的中队旗,怎样算出它的面积。(你能想出不同的方法吗?)
课堂练习
思考题:计算下面图形的面积,你能想出不同的解法吗
(单位:米)
6
5
12
10
(10+5)×6÷2+6×5
S
=
S梯形
+
S长方形
课堂练习
6
5
12
10
5×6÷2+12×5
S
=
S三角形
+
S长方形
6
5
12
10
12×10÷2
+
5×6÷2
S
=
S大三角形
+
S小三角形
6
5
12
10
12×10
-(12+6)×5÷2
S
=
S长方形
-
S梯形
6
5
12
10
6×10
÷2+(12+6)×5÷2
S
=
S三角形
+
S梯形
求组合图形的基本步骤和方法:
(1)观察、分析这个组合图形可以分割成哪些能计算面积的基本图形。
(2)找出计算基本图形面积的条件。
(3)先计算出基本图形的面积,再计算出组合图形的面积。
课堂小结
同学们,组合图形在我们日常生活应用广泛,好好学习吧,发挥你们的智慧和创造力,为美化我们的校园和家园出一份力,让我们生活的环境更加美丽可爱!
