5.3 用待定系数法确定二次函数表达式同步练习(含解析)
文档属性
| 名称 | 5.3 用待定系数法确定二次函数表达式同步练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 231.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-31 17:08:18 | ||
图片预览




文档简介
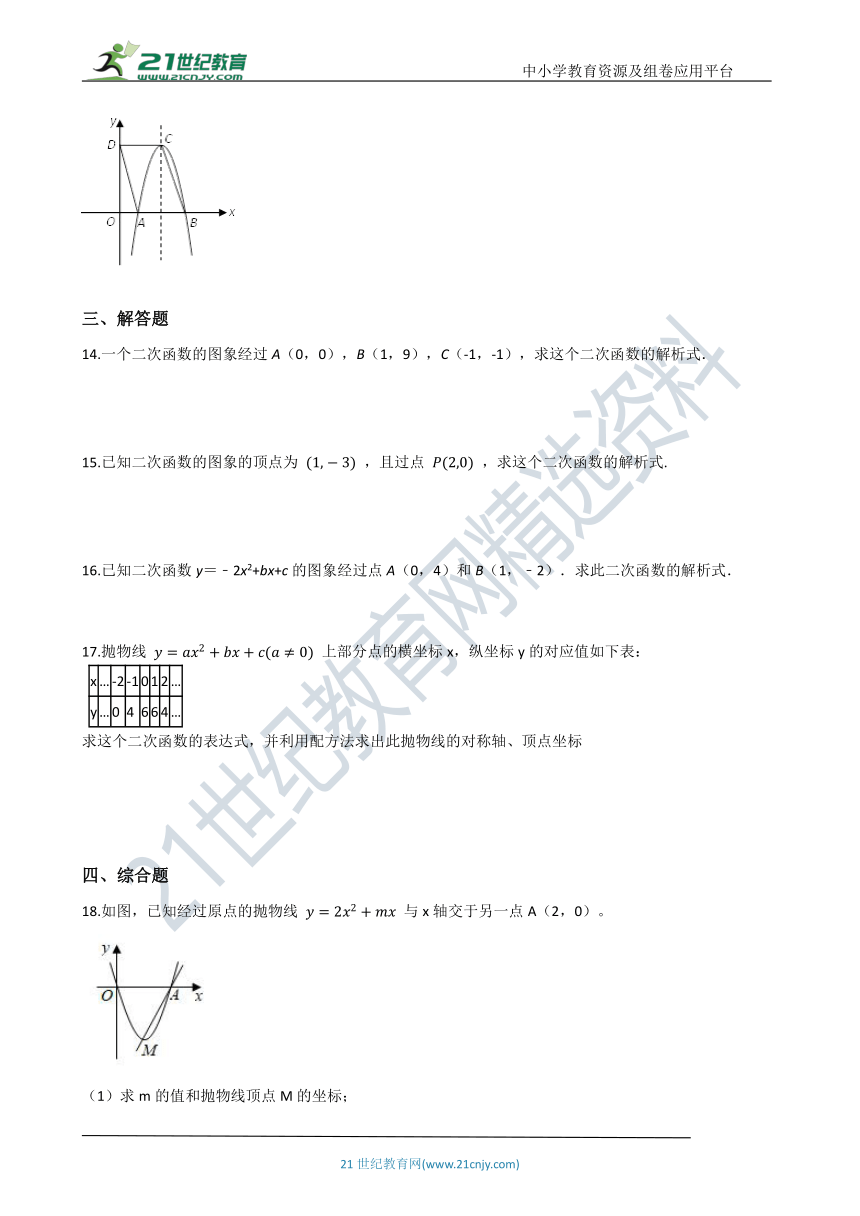
初中数学苏科版九年级下册5.3 用待定系数法确定二次函数表达式 同步练习
一、单选题
1.一个二次函数的图象的顶点坐标是 (2,?3) ,与y轴的交点是 (0,5) ,这个二次函数的解析式是(? )
A.?y=2x2?4x+11???????????B.?y=2x2?4x+5???????????C.?y=2x2?8x+5???????????D.?y=2x2+8x+5
2.二次函数的图象如图所示, 则这个二次函数的表达式为(? )
A.?y=x2+2x?3???????????B.?y=x2?2x?3???????????C.?y=?x2+2x?3???????????D.?y=?x2?2x+3
3.顶点为 (6,?0) ,开口向下,开口的大小与函数 y=13x2 的图象相同的抛物线所对应的函数是(?? )
A.?y=13(x+6)2???????????????B.?y=13(x?6)2???????????????C.?y=?13(x+6)2???????????????D.?y=?13(x?6)2
4.如图,是一条抛物线的图象,则其解析式为( )
A.?y=x2﹣2x+3?????????????????????B.?y=x2﹣2x﹣3?????????????????????C.?y=x2+2x+3?????????????????????D.?y=x2+2x-3
5.已知某二次函数的图象如图所示,则这个二次函数的解析式为( ????)
A.?y=2(x+1)2+8???????????B.?y=18(x+1)2?8???????????C.?y=29(x?1)2+8???????????D.?y=2(x?1)2?8
6.若抛物线经过 (0,1),(?1,0),(1,0) 三点,则此抛物线的表达式为(? )
A.?y=?x2+1???????????????????????B.?y=?x2?1???????????????????????C.?y=x2+1???????????????????????D.?y=x2?1
7.2019年女排世界杯于9月在日本举行,中国女排以十一连胜的骄人成绩卫冕冠军,充分展现了团队协作、顽强拼搏的女排精神.如图是某次比赛中垫球时的动作.若将垫球后排球的运动路线近似的看作抛物线,在同一竖直平面内建立如图所示的直角坐标系,已知运动员垫球时(图中点A)离球网的水平距离为5米,排球与地面的垂直距离为0.5米,排球在球网上端0.26米处(图中点B)越过球网(女子排球赛中球网上端距地面的高度为2.24米),落地时(图中点C)距球网的水平距离为2.5米,则排球运动路线的函数表达式为( ??)
A.?y=﹣ 1475x2?815x+52??????????????????????????????????B.?y=﹣ 1475x2+815x+52
C.?y= 1475x2?815x+52??????????????????????????????????????D.?y= 1475x2+815x+52
二、填空题
8.写出一个图象开口向上,顶点在x轴上的二次函数的解析式________.
9.抛物线 y=ax2+bx+c 与 x 轴的两个交点坐标分别为 (?1,0) , (3,0) ,其形状及开口方向与抛物线 y=?2x2 相同,则 y=ax2+bx+c 的函数解析式为________.
10.如果一个二次函数图象开口向下,对称轴为 x=1 ,则该二次函数表达式可以为________.(任意写出一个符合条件的即可)
11.二次函数y=ax?+bx+c图象上部分点的横坐标x,纵坐标y的对应值如下表:
x
…
﹣2
﹣1
0
1
2
…
m
…
y
…
0
4
6
6
4
…
﹣6
…
则这个二次函数的对称轴为直线x=________,m=________(m>0).
12.如图,经过原点的抛物线是二次函数 y=ax2?3x+a+1 的图象,那么a的值是________.
13.如图,平行四边形ABCD中, AB=4 ,点 D 的坐标是 (0,8) ,以点 C 为顶点的抛物线经过 x 轴上的点A , B , 则此抛物线的解析式为________.
三、解答题
14.一个二次函数的图象经过A(0,0),B(1,9),C(-1,-1),求这个二次函数的解析式.
15.已知二次函数的图象的顶点为 (1,?3) ,且过点 P(2,0) ,求这个二次函数的解析式.
16.已知二次函数y=﹣2x2+bx+c的图象经过点A(0,4)和B(1,﹣2).求此二次函数的解析式.
17.抛物线 y=ax2+bx+c(a≠0) 上部分点的横坐标x,纵坐标y的对应值如下表:
x
…
-2
-1
0
1
2
…
y
…
0
4
6
6
4
…
求这个二次函数的表达式,并利用配方法求出此抛物线的对称轴、顶点坐标
四、综合题
18.如图,已知经过原点的抛物线 y=2x2+mx 与x轴交于另一点A(2,0)。
(1)求m的值和抛物线顶点M的坐标;
(2)求直线AM的解析式。
19.如图,二次函数 y=ax2+bx+c 的图象经过 A,B,C 三点,顶点为D , 已知点B的坐标是 (1,0),OA=OC=3OB .
(1)求这个二次函数的表达式;
(2)若E是线段 AD 上的一个动点(E与 A,D 不重合),过点E作平行于y轴的直线交抛物线于点F , 求线段 EF 长度的最大值;
(3)将(1)中的函数图象平移后,表达式变为 y=ax2+2mx+1 ,若这个函数在 ?2≤x≤1 时的最大值为3,求m的值.
20.抛物线y=ax2+bx+c交x轴于A、B两点,交y轴于点C,已知抛物线的对称轴为x=1,B(3,0),C(0,﹣3),
(1)求二次函数y=ax2+bx+c的解析式;
(2)在抛物线对称轴上是否存在一点P,使点P到B、C两点距离之差最大?若存在,求出P点坐标;若不存在,请说明理由;
(3)平行于x轴的一条直线交抛物线于M、N两点,若以MN为直径的圆恰好与x轴相切,求此圆的半径.
答案解析部分
一、单选题
1.【答案】 C
解:根据题意,设二次函数解析式为 y=a(x?2)2?3 ,
将 (0,5) 代入 y=a(x?2)2?3 中,得
5=a(0?2)2?3
解得:a=2
∴二次函数解析式为 y=2(x?2)2?3 = 2x2?8x+5
故答案为:C.
2.【答案】 B
解:根据题意,二次函数对称轴为 x=1 ,与x轴的一个交点为 (?1,0) ,
则函数与x轴的另一个交点为 (3,0) ,
故设二次函数的表达式为 y=ax2+bx+c ,
函数另外两点坐标 (?1,0) , (1,?4)
可得方程组 {0=9a+3b+c0=a?b+c?4=a+b+c ,
解得方程组得 {a=1b=?2c=?3 ,
所以二次函数表达式为 y=x2?2x?3 .
故答案为B.
3.【答案】 D
解:∵抛物线的顶点为 (6,?0) ,
∴设抛物线的解析式为: y=a(x?6)2 ,
∵抛物线开口向下,开口的大小与函数 y=13x2 的图象相同,
∴a= ?13 .
∴该抛物线的解析式为: y=?13(x?6)2 .
故答案为:D.
4.【答案】 B
解:因为抛物线与x轴的交点坐标为(-1,0),(3,0),
可设交点式为y=a(x+1)(x-3),
把(0,-3)代入y=a(x+1)(x-3),
可得:-3=a(0+1)(0-3),
解得:a=1,
所以解析式为:y=x2-2x-3,
故答案为:B.
5.【答案】 D
解:由图知道,抛物线的顶点坐标是(1,-8)
故二次函数的解析式为y=2(x-1)2-8
故答案为:D.
6.【答案】 A
解:∵抛物线经过 (?1,0),(1,0)
∴设抛物线解析式为 y=a(x+1)(x?1)
把 (0,1) 代入得:
1=a(0+1)(0?1)
a=?1
∴抛物线解析式为 y=?(x+1)(x?1)=?x2+1
故答案为:A.
7.【答案】 A
解:由题意可知点A坐标为(﹣5,0.5),点B坐标为(0,2.5),点C坐标为(2.5,0)
设排球运动路线的函数解析式为:y=ax2+bx+c
∵排球经过A、B、C三点
∴ {0.5=(?5)2a?5b+c0.5=c0=2.52×a+2.5b+c
解得: {a=?1475b=?815c=2.5
∴排球运动路线的函数解析式为y=﹣ 1475x2+815x+52
故答案为:A .
二、填空题
8.【答案】 y=2(x+1)2
解:开口向上,即 a>0 ,
顶点在x轴上时,顶点纵坐标为0,即k=0,
例如 y=2(x+1)2 .(答案不唯一)
故答案为: y=2(x+1)2 .
9.【答案】 y=?2x2+4x+6
解:由题可设抛物线的交点式为: y=a(x+1)(x?3) ,
∵该抛物线的形状和开口与 y=?2x2 相同,
∴ a=?2 ,
∴抛物线的解析式为: y=?2(x+1)(x?3) ,
整理得: y=?2x2+4x+6 ,
故答案为: y=?2x2+4x+6 .
10.【答案】 y=?(x?1)2+1 (答案不唯一)
解:由题意设 y=a(x??)2+k ,
∵二次函数图象开口向下,对称轴为 x=1 ,
∴a=-1,h=1,
当k=1时,函数解析式为 y=?(x?1)2+1 ,
故答案为: y=?(x?1)2+1 .
11.【答案】 12;4
解:由表得,抛物线y=ax2+bx+c(a≠0)过点(0,6),
∴c=6,
∵抛物线y=ax2+bx+6过点(-1,4)和(1,6),
∴ {a?b+6=4a+b+6=6 ,解得: {a=?1b=1 ,
∴二次函数的表达式为:y=-x2+x+6;
∵抛物线y=ax2+bx+c(a≠0)过点(0,6)和(1,6),
∴抛物线的对称轴方程为直线x= 12 ,
当x=m时,y=-6,代入y=-x2+x+6,则有-6=-m2+m+6,
解得:m=-3或m=4,
∵m>0,
∴m=4,
故答案为: 12 ,4.
12.【答案】 -1
解:根据图示知,二次函数 y=ax2?3x+a+1 的图象经过原点(0,0),
∴0=a+1,
解得,a=-1;
故答案为:?1.
13.【答案】 y=?2x2+16x?24
解:∵四边形ABCD为平行四边形
∴CD=AB=4
∴C点坐标为 (4,8)
∴A点坐标为 (2,0) ,B点坐标为 (6,0)
设函数解析式为 y=a(x?2)(x?6) ,代入C点坐标有 8=a(4?2)(4?6)
解得 a=?2
∴函数解析式为 y=?2(x?2)(x?6) ,即 y=?2x2+16x?24
故答案为 y=?2x2+16x?24 .
三、解答题
14.【答案】 解:设二次函数的解析式为 y=ax2+bx+c .
∵抛物线经过 A(0,0) , B(1,9) , C(?1,?1) ,
∴ {c=0a+b+c=9a?b+c=?1 ,解得 {a=4b=5c=0 ,
∴ y=4x2+5x
15.【答案】 解:设所求函数的解析式为: y=a(x+?)2+k
则顶点坐标为 (??,k) ,已知顶点坐标为 (1,?3)
∴?=?1,k=?3,y=a(x?1)2?3
又 ∵ 图像经过点 p(2,0) ,代入得 0=a(2?1)2?3
解得 a=3
故解析式为 y=3(x?1)2?3
即 y=3x2?6x
16.【答案】 解:将点A(0,4)与B(1,﹣2)代入解析式,得: {c=4?2+b+c=?2 ,
解得: {b=?4c=4 ,
则此函数解析式为y=﹣2x2﹣4x+4.
17.【答案】 解:由表得,抛物线y=ax2+bx+c(a≠0)过点(0,6),
∴c=6,
∵抛物线y=ax2+bx+6过点(-1,4)和(1,6),
∴ {a?b+6=4a+b+6=6 ,
解得: {a=?1b=1 ,
∴二次函数的表达式为:y=-x2+x+6;
∴抛物线的对称轴方程为直线x= 12 ,
∵当x= 12 时,y= 254 ,
∴抛物线的顶点坐标为( 12 , 254 );
四、综合题
18.【答案】 (1)解:由题意得
8+2m=0
解之:m=-4
∴y=2x2-4x=2(x-1)2-2
∴点M(1,-2).
(2)解:设直线AM的解析式为y=kx+b
∴2k+b=0k+b=?2
k=2b=?4
∴直线AM的解析式为y=2x-4.
19.【答案】 (1)解:当 x=0 时, y=?x2+bx+c=c ,则 C(0,c) ,
∵OA=OC=3OB ,
∴A(c,0),B(?13c,0) ,
∴y=?(x+13c)(x?c)=?x2+23c+13c2 ,
∴13c2=c ,解得 c=0 (舍去)或 c=3 ,
∴ 代入二次函数 y=ax2+bx+c 解析式中,
y=?x2?2x+3 ;
(2)解: ∵ 抛物线 y=?x2?2x+3=?(x+1)2+4 ,
∴ 顶点D的坐标为 (?1,4) .
设直线 AD 的解析式为 y=kx+b ,
∵A(?3,0),?D(?1,4) ,
∴{?3k+b=0?k+b=4 ,
解得: {k=2b=0 ,
∴ 直线 AD 的解析式为 y=2x+6 .
设点E的横坐标为m,
∴E(m,2m+6),F(m,?m2?2m+3) ,
∴EF=?m2?2m+3?(2m+6)=?m2?4m?3=?(m+2)2+1 ,
∴ 当 m=?2 时, EF 最大值为1.
(3)解: ∵y=ax2+2mx+1 的图象由 y=?x2?2x+3 平移得到,
∴ 表达式可设为 y=?x2+2mx+1 ,对称轴是直线 x=m ;
①若 m解得 m=?1.5 ,不合题意,舍去;
②若 ?2≤m≤1 ,则 x=m 时函数值最大,
把 x=?m,y=3 代入 y=?x2+2mx+1 ,解得 m=±2 ,
∴m=?2 ;
③若 m>1 ,则 x=?1 时函数值最大,
把 x=?1,y=3 代入 y=?x2+2mx+1 ,
解得 m=1.5
综上所述, m=1.5 或 ?2 .
20.【答案】 (1)解:将C(0,﹣3)代入y=ax2+bx+c,
得c=﹣3.
将c=﹣3,B(3,0)代入y=ax2+bx+c,
得9a+3b+c=0.(1)
∵直线x=1是对称轴,
∴ ?b2a=1 .(2)(2分)
将(2)代入(1)得
a=1,b=﹣2.
所以,二次函数得解析式是y=x2﹣2x﹣3.
(2)解:AC与对称轴的交点P即为到B、C的距离之差最大的点.
∵C点的坐标为(0,﹣3),A点的坐标为(﹣1,0),
∴直线AC的解析式是y=﹣3x﹣3,
又∵直线x=1是对称轴,
∴点P的坐标(1,﹣6).
(3)解:设M(x1 , y)、N(x2 , y),所求圆的半径为r,
则x2﹣x1=2r,(1)
∵对称轴为直线x=1,即 x1+x22 =1,
∴x2+x1=2.(2)
由(1)、(2)得:x2=r+1.(3)
将N(r+1,y)代入解析式y=x2﹣2x﹣3,
得y=(r+1)2﹣2(r+1)﹣3.
整理得:y=r2﹣4.
由所求圆与x轴相切,得到r=|y|,即r=±y,
当y>0时,r2﹣r﹣4=0,
解得, r1=1+172 , r2=1?172 (舍去),
当y<0时,r2+r﹣4=0,
解得, r1=?1+172 , r2=?1?172 (舍去).
所以圆的半径是 1+172 或 ?1+172 .
一、单选题
1.一个二次函数的图象的顶点坐标是 (2,?3) ,与y轴的交点是 (0,5) ,这个二次函数的解析式是(? )
A.?y=2x2?4x+11???????????B.?y=2x2?4x+5???????????C.?y=2x2?8x+5???????????D.?y=2x2+8x+5
2.二次函数的图象如图所示, 则这个二次函数的表达式为(? )
A.?y=x2+2x?3???????????B.?y=x2?2x?3???????????C.?y=?x2+2x?3???????????D.?y=?x2?2x+3
3.顶点为 (6,?0) ,开口向下,开口的大小与函数 y=13x2 的图象相同的抛物线所对应的函数是(?? )
A.?y=13(x+6)2???????????????B.?y=13(x?6)2???????????????C.?y=?13(x+6)2???????????????D.?y=?13(x?6)2
4.如图,是一条抛物线的图象,则其解析式为( )
A.?y=x2﹣2x+3?????????????????????B.?y=x2﹣2x﹣3?????????????????????C.?y=x2+2x+3?????????????????????D.?y=x2+2x-3
5.已知某二次函数的图象如图所示,则这个二次函数的解析式为( ????)
A.?y=2(x+1)2+8???????????B.?y=18(x+1)2?8???????????C.?y=29(x?1)2+8???????????D.?y=2(x?1)2?8
6.若抛物线经过 (0,1),(?1,0),(1,0) 三点,则此抛物线的表达式为(? )
A.?y=?x2+1???????????????????????B.?y=?x2?1???????????????????????C.?y=x2+1???????????????????????D.?y=x2?1
7.2019年女排世界杯于9月在日本举行,中国女排以十一连胜的骄人成绩卫冕冠军,充分展现了团队协作、顽强拼搏的女排精神.如图是某次比赛中垫球时的动作.若将垫球后排球的运动路线近似的看作抛物线,在同一竖直平面内建立如图所示的直角坐标系,已知运动员垫球时(图中点A)离球网的水平距离为5米,排球与地面的垂直距离为0.5米,排球在球网上端0.26米处(图中点B)越过球网(女子排球赛中球网上端距地面的高度为2.24米),落地时(图中点C)距球网的水平距离为2.5米,则排球运动路线的函数表达式为( ??)
A.?y=﹣ 1475x2?815x+52??????????????????????????????????B.?y=﹣ 1475x2+815x+52
C.?y= 1475x2?815x+52??????????????????????????????????????D.?y= 1475x2+815x+52
二、填空题
8.写出一个图象开口向上,顶点在x轴上的二次函数的解析式________.
9.抛物线 y=ax2+bx+c 与 x 轴的两个交点坐标分别为 (?1,0) , (3,0) ,其形状及开口方向与抛物线 y=?2x2 相同,则 y=ax2+bx+c 的函数解析式为________.
10.如果一个二次函数图象开口向下,对称轴为 x=1 ,则该二次函数表达式可以为________.(任意写出一个符合条件的即可)
11.二次函数y=ax?+bx+c图象上部分点的横坐标x,纵坐标y的对应值如下表:
x
…
﹣2
﹣1
0
1
2
…
m
…
y
…
0
4
6
6
4
…
﹣6
…
则这个二次函数的对称轴为直线x=________,m=________(m>0).
12.如图,经过原点的抛物线是二次函数 y=ax2?3x+a+1 的图象,那么a的值是________.
13.如图,平行四边形ABCD中, AB=4 ,点 D 的坐标是 (0,8) ,以点 C 为顶点的抛物线经过 x 轴上的点A , B , 则此抛物线的解析式为________.
三、解答题
14.一个二次函数的图象经过A(0,0),B(1,9),C(-1,-1),求这个二次函数的解析式.
15.已知二次函数的图象的顶点为 (1,?3) ,且过点 P(2,0) ,求这个二次函数的解析式.
16.已知二次函数y=﹣2x2+bx+c的图象经过点A(0,4)和B(1,﹣2).求此二次函数的解析式.
17.抛物线 y=ax2+bx+c(a≠0) 上部分点的横坐标x,纵坐标y的对应值如下表:
x
…
-2
-1
0
1
2
…
y
…
0
4
6
6
4
…
求这个二次函数的表达式,并利用配方法求出此抛物线的对称轴、顶点坐标
四、综合题
18.如图,已知经过原点的抛物线 y=2x2+mx 与x轴交于另一点A(2,0)。
(1)求m的值和抛物线顶点M的坐标;
(2)求直线AM的解析式。
19.如图,二次函数 y=ax2+bx+c 的图象经过 A,B,C 三点,顶点为D , 已知点B的坐标是 (1,0),OA=OC=3OB .
(1)求这个二次函数的表达式;
(2)若E是线段 AD 上的一个动点(E与 A,D 不重合),过点E作平行于y轴的直线交抛物线于点F , 求线段 EF 长度的最大值;
(3)将(1)中的函数图象平移后,表达式变为 y=ax2+2mx+1 ,若这个函数在 ?2≤x≤1 时的最大值为3,求m的值.
20.抛物线y=ax2+bx+c交x轴于A、B两点,交y轴于点C,已知抛物线的对称轴为x=1,B(3,0),C(0,﹣3),
(1)求二次函数y=ax2+bx+c的解析式;
(2)在抛物线对称轴上是否存在一点P,使点P到B、C两点距离之差最大?若存在,求出P点坐标;若不存在,请说明理由;
(3)平行于x轴的一条直线交抛物线于M、N两点,若以MN为直径的圆恰好与x轴相切,求此圆的半径.
答案解析部分
一、单选题
1.【答案】 C
解:根据题意,设二次函数解析式为 y=a(x?2)2?3 ,
将 (0,5) 代入 y=a(x?2)2?3 中,得
5=a(0?2)2?3
解得:a=2
∴二次函数解析式为 y=2(x?2)2?3 = 2x2?8x+5
故答案为:C.
2.【答案】 B
解:根据题意,二次函数对称轴为 x=1 ,与x轴的一个交点为 (?1,0) ,
则函数与x轴的另一个交点为 (3,0) ,
故设二次函数的表达式为 y=ax2+bx+c ,
函数另外两点坐标 (?1,0) , (1,?4)
可得方程组 {0=9a+3b+c0=a?b+c?4=a+b+c ,
解得方程组得 {a=1b=?2c=?3 ,
所以二次函数表达式为 y=x2?2x?3 .
故答案为B.
3.【答案】 D
解:∵抛物线的顶点为 (6,?0) ,
∴设抛物线的解析式为: y=a(x?6)2 ,
∵抛物线开口向下,开口的大小与函数 y=13x2 的图象相同,
∴a= ?13 .
∴该抛物线的解析式为: y=?13(x?6)2 .
故答案为:D.
4.【答案】 B
解:因为抛物线与x轴的交点坐标为(-1,0),(3,0),
可设交点式为y=a(x+1)(x-3),
把(0,-3)代入y=a(x+1)(x-3),
可得:-3=a(0+1)(0-3),
解得:a=1,
所以解析式为:y=x2-2x-3,
故答案为:B.
5.【答案】 D
解:由图知道,抛物线的顶点坐标是(1,-8)
故二次函数的解析式为y=2(x-1)2-8
故答案为:D.
6.【答案】 A
解:∵抛物线经过 (?1,0),(1,0)
∴设抛物线解析式为 y=a(x+1)(x?1)
把 (0,1) 代入得:
1=a(0+1)(0?1)
a=?1
∴抛物线解析式为 y=?(x+1)(x?1)=?x2+1
故答案为:A.
7.【答案】 A
解:由题意可知点A坐标为(﹣5,0.5),点B坐标为(0,2.5),点C坐标为(2.5,0)
设排球运动路线的函数解析式为:y=ax2+bx+c
∵排球经过A、B、C三点
∴ {0.5=(?5)2a?5b+c0.5=c0=2.52×a+2.5b+c
解得: {a=?1475b=?815c=2.5
∴排球运动路线的函数解析式为y=﹣ 1475x2+815x+52
故答案为:A .
二、填空题
8.【答案】 y=2(x+1)2
解:开口向上,即 a>0 ,
顶点在x轴上时,顶点纵坐标为0,即k=0,
例如 y=2(x+1)2 .(答案不唯一)
故答案为: y=2(x+1)2 .
9.【答案】 y=?2x2+4x+6
解:由题可设抛物线的交点式为: y=a(x+1)(x?3) ,
∵该抛物线的形状和开口与 y=?2x2 相同,
∴ a=?2 ,
∴抛物线的解析式为: y=?2(x+1)(x?3) ,
整理得: y=?2x2+4x+6 ,
故答案为: y=?2x2+4x+6 .
10.【答案】 y=?(x?1)2+1 (答案不唯一)
解:由题意设 y=a(x??)2+k ,
∵二次函数图象开口向下,对称轴为 x=1 ,
∴a=-1,h=1,
当k=1时,函数解析式为 y=?(x?1)2+1 ,
故答案为: y=?(x?1)2+1 .
11.【答案】 12;4
解:由表得,抛物线y=ax2+bx+c(a≠0)过点(0,6),
∴c=6,
∵抛物线y=ax2+bx+6过点(-1,4)和(1,6),
∴ {a?b+6=4a+b+6=6 ,解得: {a=?1b=1 ,
∴二次函数的表达式为:y=-x2+x+6;
∵抛物线y=ax2+bx+c(a≠0)过点(0,6)和(1,6),
∴抛物线的对称轴方程为直线x= 12 ,
当x=m时,y=-6,代入y=-x2+x+6,则有-6=-m2+m+6,
解得:m=-3或m=4,
∵m>0,
∴m=4,
故答案为: 12 ,4.
12.【答案】 -1
解:根据图示知,二次函数 y=ax2?3x+a+1 的图象经过原点(0,0),
∴0=a+1,
解得,a=-1;
故答案为:?1.
13.【答案】 y=?2x2+16x?24
解:∵四边形ABCD为平行四边形
∴CD=AB=4
∴C点坐标为 (4,8)
∴A点坐标为 (2,0) ,B点坐标为 (6,0)
设函数解析式为 y=a(x?2)(x?6) ,代入C点坐标有 8=a(4?2)(4?6)
解得 a=?2
∴函数解析式为 y=?2(x?2)(x?6) ,即 y=?2x2+16x?24
故答案为 y=?2x2+16x?24 .
三、解答题
14.【答案】 解:设二次函数的解析式为 y=ax2+bx+c .
∵抛物线经过 A(0,0) , B(1,9) , C(?1,?1) ,
∴ {c=0a+b+c=9a?b+c=?1 ,解得 {a=4b=5c=0 ,
∴ y=4x2+5x
15.【答案】 解:设所求函数的解析式为: y=a(x+?)2+k
则顶点坐标为 (??,k) ,已知顶点坐标为 (1,?3)
∴?=?1,k=?3,y=a(x?1)2?3
又 ∵ 图像经过点 p(2,0) ,代入得 0=a(2?1)2?3
解得 a=3
故解析式为 y=3(x?1)2?3
即 y=3x2?6x
16.【答案】 解:将点A(0,4)与B(1,﹣2)代入解析式,得: {c=4?2+b+c=?2 ,
解得: {b=?4c=4 ,
则此函数解析式为y=﹣2x2﹣4x+4.
17.【答案】 解:由表得,抛物线y=ax2+bx+c(a≠0)过点(0,6),
∴c=6,
∵抛物线y=ax2+bx+6过点(-1,4)和(1,6),
∴ {a?b+6=4a+b+6=6 ,
解得: {a=?1b=1 ,
∴二次函数的表达式为:y=-x2+x+6;
∴抛物线的对称轴方程为直线x= 12 ,
∵当x= 12 时,y= 254 ,
∴抛物线的顶点坐标为( 12 , 254 );
四、综合题
18.【答案】 (1)解:由题意得
8+2m=0
解之:m=-4
∴y=2x2-4x=2(x-1)2-2
∴点M(1,-2).
(2)解:设直线AM的解析式为y=kx+b
∴2k+b=0k+b=?2
k=2b=?4
∴直线AM的解析式为y=2x-4.
19.【答案】 (1)解:当 x=0 时, y=?x2+bx+c=c ,则 C(0,c) ,
∵OA=OC=3OB ,
∴A(c,0),B(?13c,0) ,
∴y=?(x+13c)(x?c)=?x2+23c+13c2 ,
∴13c2=c ,解得 c=0 (舍去)或 c=3 ,
∴ 代入二次函数 y=ax2+bx+c 解析式中,
y=?x2?2x+3 ;
(2)解: ∵ 抛物线 y=?x2?2x+3=?(x+1)2+4 ,
∴ 顶点D的坐标为 (?1,4) .
设直线 AD 的解析式为 y=kx+b ,
∵A(?3,0),?D(?1,4) ,
∴{?3k+b=0?k+b=4 ,
解得: {k=2b=0 ,
∴ 直线 AD 的解析式为 y=2x+6 .
设点E的横坐标为m,
∴E(m,2m+6),F(m,?m2?2m+3) ,
∴EF=?m2?2m+3?(2m+6)=?m2?4m?3=?(m+2)2+1 ,
∴ 当 m=?2 时, EF 最大值为1.
(3)解: ∵y=ax2+2mx+1 的图象由 y=?x2?2x+3 平移得到,
∴ 表达式可设为 y=?x2+2mx+1 ,对称轴是直线 x=m ;
①若 m解得 m=?1.5 ,不合题意,舍去;
②若 ?2≤m≤1 ,则 x=m 时函数值最大,
把 x=?m,y=3 代入 y=?x2+2mx+1 ,解得 m=±2 ,
∴m=?2 ;
③若 m>1 ,则 x=?1 时函数值最大,
把 x=?1,y=3 代入 y=?x2+2mx+1 ,
解得 m=1.5
综上所述, m=1.5 或 ?2 .
20.【答案】 (1)解:将C(0,﹣3)代入y=ax2+bx+c,
得c=﹣3.
将c=﹣3,B(3,0)代入y=ax2+bx+c,
得9a+3b+c=0.(1)
∵直线x=1是对称轴,
∴ ?b2a=1 .(2)(2分)
将(2)代入(1)得
a=1,b=﹣2.
所以,二次函数得解析式是y=x2﹣2x﹣3.
(2)解:AC与对称轴的交点P即为到B、C的距离之差最大的点.
∵C点的坐标为(0,﹣3),A点的坐标为(﹣1,0),
∴直线AC的解析式是y=﹣3x﹣3,
又∵直线x=1是对称轴,
∴点P的坐标(1,﹣6).
(3)解:设M(x1 , y)、N(x2 , y),所求圆的半径为r,
则x2﹣x1=2r,(1)
∵对称轴为直线x=1,即 x1+x22 =1,
∴x2+x1=2.(2)
由(1)、(2)得:x2=r+1.(3)
将N(r+1,y)代入解析式y=x2﹣2x﹣3,
得y=(r+1)2﹣2(r+1)﹣3.
整理得:y=r2﹣4.
由所求圆与x轴相切,得到r=|y|,即r=±y,
当y>0时,r2﹣r﹣4=0,
解得, r1=1+172 , r2=1?172 (舍去),
当y<0时,r2+r﹣4=0,
解得, r1=?1+172 , r2=?1?172 (舍去).
所以圆的半径是 1+172 或 ?1+172 .
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
