5.5 用二次函数解决问题同步练习(含解析)
文档属性
| 名称 | 5.5 用二次函数解决问题同步练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 344.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-31 17:11:15 | ||
图片预览




文档简介
初中数学苏科版九年级下册5.5 用二次函数解决问题 同步练习
一、单选题
1.从地面竖直向上抛出一小球,小球的高度h(单位:m)与小球运动时间t(单位:s)之间的函数关系如图所示.下列结论:①小球抛出3秒时达到最高点;②小球从抛出到落地经过的路程是80m;③小球的高度h=20时,t=1s或5s.④小球抛出2秒后的高度是35m.其中正确的有(?? )
A.?①②??????????????????????????????????B.?②③??????????????????????????????????C.?①③④??????????????????????????????????D.?①②③
2.图(1)是一个横断面为抛物线形状的拱桥,当水面在L时,拱顶(拱桥洞的最高点)离水面2m,水面宽为4m.如果水面宽度为6m,则水面下降 (?? )
A.?3.5 m????????????????????????????????????B.?3 m????????????????????????????????????C.?2.5 m????????????????????????????????????D.?2 m
3.竖直向上的小球离地面的高度h(米)与时间t(秒)的关系函数关系式为h=-2t2+mt+ 258 ,若小球经过 74 秒落地,则小球在上抛过程中,第(?? )秒离地面最高.
A.?37??????????????????????????????????????????B.?47??????????????????????????????????????????C.?34??????????????????????????????????????????D.?43
4.如图,已知二次函数y=mx2-4mx+3m(m>0)的图像与x轴交于A,B两点,与y轴交于点C,连接AC、BC,若CA平分∠OCB,则m的值为(??? )
A.?3??????????????????????????????????????B.?2??????????????????????????????????????C.?22??????????????????????????????????????D.?33
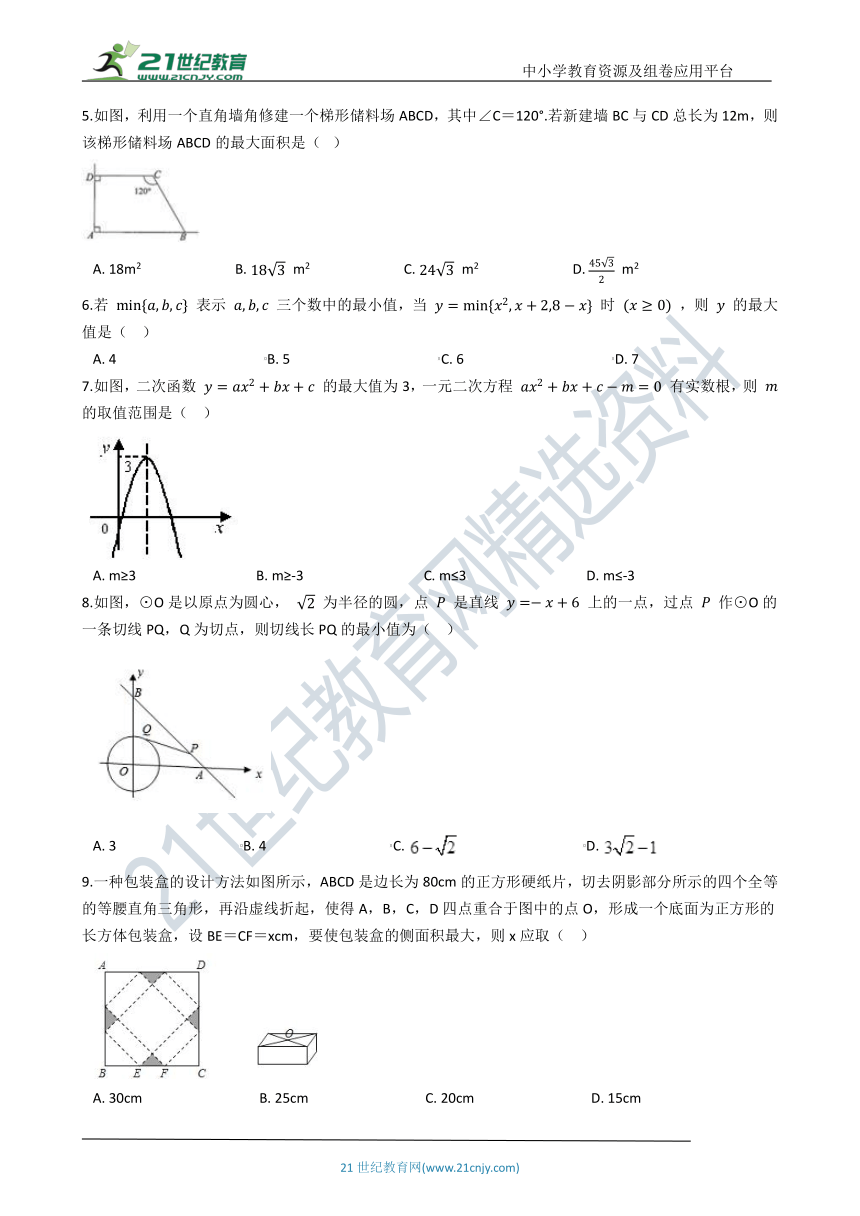
5.如图,利用一个直角墙角修建一个梯形储料场ABCD,其中∠C=120°.若新建墙BC与CD总长为12m,则该梯形储料场ABCD的最大面积是(? )
A.?18m2???????????????????????????B.?183 m2???????????????????????????C.?243 m2???????????????????????????D.?4532 m2
6.若 min{a,b,c} 表示 a,b,c 三个数中的最小值,当 y=min{x2,x+2,8?x} 时 (x≥0) ,则 y 的最大值是(?? )
A.?4???????????????????????????????????????????B.?5???????????????????????????????????????????C.?6???????????????????????????????????????????D.?7
7.如图,二次函数 y=ax2+bx+c 的最大值为3,一元二次方程 ax2+bx+c?m=0 有实数根,则 m 的取值范围是(?? )
A.?m≥3???????????????????????????????????B.?m≥-3???????????????????????????????????C.?m≤3???????????????????????????????????D.?m≤-3
8.如图,⊙O是以原点为圆心, 2 为半径的圆,点 P 是直线 y=?x+6 上的一点,过点 P 作⊙O的一条切线PQ,Q为切点,则切线长PQ的最小值为(?? )
A.?3????????????????????????????????????B.?4????????????????????????????????????C.?????????????????????????????????????D.?
9.一种包装盒的设计方法如图所示,ABCD是边长为80cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得A,B,C,D四点重合于图中的点O,形成一个底面为正方形的长方体包装盒,设BE=CF=xcm,要使包装盒的侧面积最大,则x应取( ??)
A.?30cm??????????????????????????????????B.?25cm??????????????????????????????????C.?20cm??????????????????????????????????D.?15cm
二、填空题
10.王翔同学在一次跳高训练中采用了背跃式,跳跃路线正好和抛物线 y=?35x2+65x+1 相吻合,那么他能跳过的最大高度为________m.
11.道路的隔离栏通常会涂上醒目的颜色,呈抛物线形状(如图 1 ),图 2 是一个长为 2 米,宽为 1 米的矩形隔离栏,中间被 4 根栏杆五等分,每根栏杆的下面一部分涂上醒目的蓝色,颜色的分界处(点 E ,点 P )以及点 A ,点 B 落在同一条抛物线上,若第 1 根栏杆涂色部分( EF )与第 2 根栏杆未涂色部分( PQ )长度相等,则 EF 的长度是________.
12.如图,某大桥有一段抛物线形的拱梁,抛物线的解析式为y=ax2+bx,小强骑自行车从拱梁一端O匀速穿过拱梁部分的桥面OC,当小强骑自行车行驶到6分钟和14分钟时拱梁的高度相同,则小强骑自行车通过拱梁部分的桥面OC共需________分钟.
13.某大学的校门如图所示是抛物线形水泥建筑物,大门内侧的地面宽度为8米,两侧距地面4米高处各有一个挂校名横匾用的铁环,两铁环的水平距离为6米,那么校门内侧距地面的高是________米.
三、解答题
14.某汽车出租公司以每辆汽车月租费3000元,100辆汽车可以全部租出.若每辆汽车的月租费每增加50元,则将少租1辆汽车.已知每辆租出的汽车支付月维护费200元,问每月租出多少辆汽车时,该出租公司的月收益最大?最大月收益是多少?
15.如图所示,公园要造圆形的喷水池,在水池中央垂直于水面处安装一个柱子OA,O恰在水面中心,OA=1.25m,由柱子顶端A处的喷头向外喷水,水流在各个方向沿形状相同的抛物线路线落下,为使水流形状较为漂亮,要求设计成水流在离OA距离为1m处达到距水面距离最大,高度2.25m.若不计其他因素,那么水池的半径至少要多少米才能使喷出的水流不致落到池外?
16.某商场将进价40元一个的某种商品按50元一个售出时,每月能卖出500个.商场想了两个方案来增加利润:
方案一:提高价格,但这种商品每个售价涨价1元,销售量就减少10个;
方案二:售价不变,但发资料做广告.已知当这种商品每月的广告费用为m(千元)时,每月销售量将是原销售量的p倍,且p = .
试通过计算,请你判断商场为赚得更大的利润应选择哪种方案?请说明你判断的理由!
17.公司投资750万元,成功研制出一种市场需求量较大的产品,并再投入资金1750万元进行相关生产设备的改进.已知生产过程中,每件产品的成本为60元.在销售过程中发现,当销售单价定为120元时,年销售量为24万件;销售单价每增加10元,年销售量将减少1万件.设销售单价为x(元)(x>120),年销售量为y(万件),第一年年获利(年获利=年销售额﹣生产成本)为z(万元).
(1)求出y与x之间,z与x之间的函数关系式;
(2)该公司能否在第一年收回投资.
18.如图,抛物线y=ax2+bx+c与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于C(0,﹣3).
(1)求抛物线的解析式;
(2)D是y轴正半轴上的点,OD=3,在线段BD上任取一点E(不与B,D重合),经过A,B,E三点的圆交直线BC于点F,
①试说明EF是圆的直径;
②判断△AEF的形状,并说明理由.
四、综合题
19.某商场经营某种品牌的玩具,购进时的单价是40元,根据市场调查:在一段时间内,销售单价是50元时,销售量是600件,而销售单价每涨2元,就会少售出20件玩具.
(1)不妨设该种品牌玩具的销售单价为x元(x>50),请你分别用x的代数式来表示销售量y件和销售该品牌玩具获得利润ω元,并把结果填写在表格中:
销售单价(元)
x
销售量y(件)
________
销售玩具获得利润ω(元)
________
(2)在(1)问条件下,若玩具厂规定该品牌玩具销售单价不低于54元,且商场要完成不少于400件的销售任务,求商场销售该品牌玩具获得的最大利润是多少元?
20.某水果销售店在草莓销售旺季,试销售成本为每千克20元的草莓,规定试销期间销售单价不低于成本单价,也不高于每千克40元,经试销发现,销售量y(千克)与销售单价x(元)符合一次函数关系,如图是y与x的函数关系图象.
(1)求y与x的函数解析式;
(2)设该水果销售店试销草莓获得的利润为W元,求W的最大值.
21.如图,在一次高尔夫球的比赛中,某运动员在原点O处击球,目标是离击球点10米远的球洞,球的飞行路线是一条抛物线,结果球的落地点距离球洞2米,(击球点、落地点、球洞三点共线)球在空中最高处达3.2米.
(1)求表示球飞行的高度y(单位:米)与表示球飞出的水平距离x(单位:米)之间的函数关系式;
(2)当球的飞行高度不低于3米时,求x的取值范围.
答案解析部分
一、单选题
1.【答案】 A
解:由图象可知,点(0,0),(6,0),(3,40)在抛物线上,顶点为(3,40),
设函数解析式为h=a(t﹣3)2+40,
将(0,0)代入得:0=a(0﹣3)2+40,
解得:a= ?409 ,
∴h= ?409 (t﹣3)2+40.
①∵顶点为(3,40),
∴小球抛出3秒时达到最高点,故①正确;
②小球从抛出到落地经过的路程应为该小球从上升到落下的长度,故为40×2=80m,故②正确;
③令h=20,则20= ?409 (t﹣3)2+40,
解得t=3± 322 ,故③错误;
④令t=2,则h= ?409 (2﹣3)2+40= 3209 m,故④错误.
综上,正确的有①②.
故答案为:A.
2.【答案】 C
解:设此函数解析式为: y=ax2 , a≠0 ;
那么 (2,?2) 应在此函数解析式上.
则 ?2=4a
即得 a=?12 ,
那么 y=?12x2 .
当x=3时, y=?12×32=?4.5
∴水面下降(-2)-(-4.5)=2.5(米)
故答案为:C.
3.【答案】 A
解:∵竖直上抛的小球离地面的高度h(米)与时间t(秒)的函数关系式为h=﹣2t2+mt+ 258 ,小球经过 74 秒落地,
∴t= 74 时,h=0,
则0=﹣2×( 74 )2+ 74 m+ 258 ,
解得:m= 127 ,
当t= ?b2a = ?1272×(?2) = 37 时,h最大,
故答案为: 37 .
4.【答案】 D
解:过点A作AD∥BC
∴∠DAC=∠ACB
∵CA平分∠OCB
∴∠OCA=∠ACB
∴∠DCA=∠DAC
∴DA=CD
当x=0时y=3m
∴点C(0,3m)
∴OC=3m,
当y=0时mx2-4mx+3m=0??
∵m≠0
∴x2-4x+3=0
解之:x1=1,x2=3
∴点A(1,0),点B(3,0)
∴OA=1,OB=3.
∵AD∥BC
∴ODOC=OAOB即OD3m=13
解之:OD=m,
∴AD=CD=OC-OD=3m-m=2m,
在Rt△OAD中,
AD2-OD2=OA2
∴(2m)2-m2=12
解之:m1=33 , m2=?33<0(舍去).
故答案为:D.
5.【答案】 C
解:如图,过点C作CE⊥AB于E,?
则四边形ADCE为矩形,设CD=AE=x,∠DCE=∠CEB=90°,?则∠BCE=∠BCD-∠DCE=30°,BC=12-x,
在Rt△CBE中,∵∠CEB=90°,
∴BE=12BC=6?12x
∴AD=CE=3BE=63?32x,AB=AE+BE=x+6?12x=12x+6
∴梯形ABCD面积 S=12(CD+AB)?CE=12(x+12x+6)?(63?32x)=?338x2+33x+183=?3388 (x?4)2+243
∴当x=4时,S最大=24 3 .?
即CD长为4 m时,使梯形储料场ABCD的面积最大为24 3 ?m2。
故答案为:C。
6.【答案】 B
解:如图,
当x+2=8-x时,y有最大值,
即:x=3,y最大=3+2=5.
故答案为:B.
7.【答案】 C
解:方程ax2+bx+c-m=0有实数根,相当于y=ax2+bx+c(a≠0)平移m个单位与x轴有交点,
又∵图象最高点y=3,
∴二次函数最多可以向下平移三个单位,
∴m≤3,
故答案为:C.
8.【答案】 B
解:∵P在直线y=-x+6上,
∴设P坐标为(m,6-m),
连接OQ,OP,由PQ为圆O的切线,得到PQ⊥OQ,
在Rt△OPQ中,根据勾股定理得:OP2=PQ2+OQ2 ,
∴PQ2=m2+(6-m)2-2=2m2-12m+34=2(m-3)2+16,
则当m=3时,切线长PQ的最小值为4.
故答案为:B.
9.【答案】 C
解:设包装盒的高为h(cm),底面边长为a(cm),则a= 2 x,h= 2 (40﹣x),0<x<40.S=4ah=8x(40﹣x)=﹣8(x﹣20)2+3200,∴当x=20cm时,S取最大值.故答案为:C.
二、填空题
10.【答案】 85
解:∵ y=?35x2+65x+1
= ?35(x2?2x?53)
= ?35[(x?1)2?83]
= ?35(x?1)2+85
∴抛物线的最大值为 85 ,
故他能跳过的最大高度为 85 .
11.【答案】 0.4
解:如图,
令P下方的点为H,以AB中点为原点,建立坐标系xOy,则A(1,0),B(-1,O),
设抛物线的方程为y=ax2+bx+c
∴抛物线的对称轴为x=0,则 ?b2a =0,即b=0.
∴y=ax2 +c.
将A(1,0)代入得a+c=0,则c=-a.
∴y=ax2-a.
∵OH=2× 15 × 12 =0.2,则点H的坐标为(-0.2,0)
同理可得:点F的坐标为(-0.6,0).
∴PH=a×(-0.2)2-a=-0.96a
EF=a×(-0.6)2-a=-0.64a.
又∵PQ=EF=1-(-0.96a)=-0.64a
∴1+0.96a=-0.64a.
解得a= ?58 .
∴y= ?58 x2+ 58 .
∴EF=( ?58 )×(-0.6)2+ 58 = 25 .
故答案为:0.4.
12.【答案】 20
解:如图所示:
设在6分钟时到达A点,在14分钟时到达B,
∵6分钟和14分钟时拱梁的高度相同,
∴A,B关于对称轴对称.则从A到B需要8分钟,则从A到D需要4分钟.
∴从O到D需要6+4=10分.
∴从O到C需要2×10=20分.
故答案为:20.
13.【答案】 647
解:建立如图所示的平面直角坐标系,
设抛物线的解析式为 y=ax2+c ,
由题意得:此抛物线的图象经过点 (82,0) 和点 (62,4) ,即点 (4,0) 和点 (3,4) ,
将点 (4,0) 和点 (3,4) 代入得: {16a+c=09a+c=4 ,
解得 {a=?47c=647 ,
则抛物线的解析式为 y=?47x2+647 ,
当 x=0 时, y=647 ,
即校门内侧距地面的高是 647 米,
故答案为: 647 .
三、解答题
14.【答案】 解:设每月租出 x 辆汽车时,该出租公司的月收益最大,月收益为 y 元.
根据题意得: y=[3000+50(100?x)]x?200x ,
即: y=?50x2+7800x .
配方得: y=?50(x?78)2+304200 .
故每月租出78辆汽车时,该出租公司的月收益最大,最大月收益是304200元.
15.【答案】 解:以地面上任一条直线为x轴,OA为y轴建立直角坐标系,
设y=a(x-1)2+2.25,则当x=0时,y=1.25,故a+2.25=1,a=-1.
由y=0得-(x-1)2+2.25=0,得(x-1)2=2.25,解得x1=2.5,x2=-0.5(舍去)
故水池的半径至少要2.5米.
16.【答案】 解:设涨价x元,利润为y元,则
方案一:涨价x元时,该商品每一件利润为:50+x?40,销售量为:500?10x,
∴ y=(50+x?40)(500?10x)=?10x2+400x+5000=?10(x?20)2+9000 ,
∵当x=20时,y最大=9000,
∴方案一的最大利润为9000元;
方案二:该商品售价利润为=(50?40)×500p,广告费用为:1000m元,
∴ y=(50?40)×500p?1000m=?2000m2+9000m=?2000(m?2.25)2+10125 ,
∴方案二的最大利润为10125元;
∴选择方案二能获得更大的利润.
17.【答案】 解:由题意得,
y=24﹣x?12010 , 即y=﹣110x+36,
z=(x﹣60)(﹣110x+36)=﹣110x2+42x﹣2160;
(2)z=﹣110x2+42x﹣2160=﹣110(x﹣210)2+2250,
当x=210时,第一年的年最大利润为2250万元,
∵2250<750+1750,
∴公司不能在第一年收回投资.
18.【答案】 解:(1)∵抛物线y=ax2+bx+c与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于C(0,﹣3),
∴有0=a?b+c0=9a+3b+c?3=c , 解得a=1b=?2c=?3 ,
∴抛物线的解析式为y=x2﹣2x﹣3.
(2)按照题意画出图形,如下图,
①∵B点坐标(3,0)、C点坐标(0,﹣3),
∴OB=OC=3,
∴△BOC为等腰直角三角形,
∴∠CBO=45°,
又∵D是y轴正半轴上的点,OD=3,
∴△BOD为等腰直接三角形,
∴∠OBD=45°,
∠CBD=∠CBO+∠OBD=45°+45°=90°,
即∠FBE=90°,
∴EF是圆的直径.
②∵∠CBO=∠OBD=45°,∠AFE=∠OBD,∠AEF=∠CBO(在同圆中,同弧所对的圆周角相等),
∴∠AEF=∠AFE=45°,
∴∠FAE=90°,AE=AF,
∴△AEF是等腰直角三角形.
四、综合题
19.【答案】 (1)-10x+1100;?10x2+1500x?44000
(2)解:由题得 {x≥54?10x+1100≥400 ,解得: 54≤x≤70 ?
w=?10(x?75)2+12250 ,
∴ x=70 时取最大值,最大值为12000.
答:商场的最大利润为12000元
解:(1)由销售单价每涨1元,就会少售出10件玩具得,
①: y=600?(x?50)×10=1100?10x,
②: w=(1100?10x)(x?40)=?10x2+1500x?44000;
故答案为:① ?10x+1100;②?10x2+1500x?44000;
20.【答案】 (1)解:设y与x的函数关系式为y=kx+b,
根据题意,得: {20k+b=30030k+b=280 ,解得: {k=?2b=340 ,
∴y与x的函数解析式为y=-2x+340(20≤x≤40).
(2)解:由已知得:W=(x-20)(-2x+340)
=-2x2+380x-6800
=-2×(x-95)2+11250,
∵-2<0,
∴当x≤95时,W随x的增大而增大,
∵20≤x≤40,
∴当x=40时,W最大,最大值为-2×(40-95)2+11250=5200元.
21.【答案】 (1)解:抛物线过原点 ,设抛物线解析式为: y=ax2+bx ,
球的落地点距离=10-2=8米,则落地点坐标为(8,0),
∴ 64a+8b=0 ,
∴ 8a+b=0 ,
球在空中最高处达3.2米,
∴ ?b24a=3.2 ,
∴ b2+12.8a=0 ,
∴ {8a+b=0b2+12.8a=0 ,
解得: {a=?0.2b=1.6 ,
∴ y=?0.2x2+1.6x ;
(2)解:当y=3时, ?0.2x2+1.6x=3 ,
整理得: x2?8x+15=0 ,
∴ (x?3)(x?5)=0 ,
∴ x=3 或 x=5 ,
∵ a=?0.2<0 ,抛物线开口向下,球的飞行高度不低于3米应在两根之间,
∴球的飞行高度不低于3米, x的取值范围是 3≤x≤5 .
一、单选题
1.从地面竖直向上抛出一小球,小球的高度h(单位:m)与小球运动时间t(单位:s)之间的函数关系如图所示.下列结论:①小球抛出3秒时达到最高点;②小球从抛出到落地经过的路程是80m;③小球的高度h=20时,t=1s或5s.④小球抛出2秒后的高度是35m.其中正确的有(?? )
A.?①②??????????????????????????????????B.?②③??????????????????????????????????C.?①③④??????????????????????????????????D.?①②③
2.图(1)是一个横断面为抛物线形状的拱桥,当水面在L时,拱顶(拱桥洞的最高点)离水面2m,水面宽为4m.如果水面宽度为6m,则水面下降 (?? )
A.?3.5 m????????????????????????????????????B.?3 m????????????????????????????????????C.?2.5 m????????????????????????????????????D.?2 m
3.竖直向上的小球离地面的高度h(米)与时间t(秒)的关系函数关系式为h=-2t2+mt+ 258 ,若小球经过 74 秒落地,则小球在上抛过程中,第(?? )秒离地面最高.
A.?37??????????????????????????????????????????B.?47??????????????????????????????????????????C.?34??????????????????????????????????????????D.?43
4.如图,已知二次函数y=mx2-4mx+3m(m>0)的图像与x轴交于A,B两点,与y轴交于点C,连接AC、BC,若CA平分∠OCB,则m的值为(??? )
A.?3??????????????????????????????????????B.?2??????????????????????????????????????C.?22??????????????????????????????????????D.?33
5.如图,利用一个直角墙角修建一个梯形储料场ABCD,其中∠C=120°.若新建墙BC与CD总长为12m,则该梯形储料场ABCD的最大面积是(? )
A.?18m2???????????????????????????B.?183 m2???????????????????????????C.?243 m2???????????????????????????D.?4532 m2
6.若 min{a,b,c} 表示 a,b,c 三个数中的最小值,当 y=min{x2,x+2,8?x} 时 (x≥0) ,则 y 的最大值是(?? )
A.?4???????????????????????????????????????????B.?5???????????????????????????????????????????C.?6???????????????????????????????????????????D.?7
7.如图,二次函数 y=ax2+bx+c 的最大值为3,一元二次方程 ax2+bx+c?m=0 有实数根,则 m 的取值范围是(?? )
A.?m≥3???????????????????????????????????B.?m≥-3???????????????????????????????????C.?m≤3???????????????????????????????????D.?m≤-3
8.如图,⊙O是以原点为圆心, 2 为半径的圆,点 P 是直线 y=?x+6 上的一点,过点 P 作⊙O的一条切线PQ,Q为切点,则切线长PQ的最小值为(?? )
A.?3????????????????????????????????????B.?4????????????????????????????????????C.?????????????????????????????????????D.?
9.一种包装盒的设计方法如图所示,ABCD是边长为80cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得A,B,C,D四点重合于图中的点O,形成一个底面为正方形的长方体包装盒,设BE=CF=xcm,要使包装盒的侧面积最大,则x应取( ??)
A.?30cm??????????????????????????????????B.?25cm??????????????????????????????????C.?20cm??????????????????????????????????D.?15cm
二、填空题
10.王翔同学在一次跳高训练中采用了背跃式,跳跃路线正好和抛物线 y=?35x2+65x+1 相吻合,那么他能跳过的最大高度为________m.
11.道路的隔离栏通常会涂上醒目的颜色,呈抛物线形状(如图 1 ),图 2 是一个长为 2 米,宽为 1 米的矩形隔离栏,中间被 4 根栏杆五等分,每根栏杆的下面一部分涂上醒目的蓝色,颜色的分界处(点 E ,点 P )以及点 A ,点 B 落在同一条抛物线上,若第 1 根栏杆涂色部分( EF )与第 2 根栏杆未涂色部分( PQ )长度相等,则 EF 的长度是________.
12.如图,某大桥有一段抛物线形的拱梁,抛物线的解析式为y=ax2+bx,小强骑自行车从拱梁一端O匀速穿过拱梁部分的桥面OC,当小强骑自行车行驶到6分钟和14分钟时拱梁的高度相同,则小强骑自行车通过拱梁部分的桥面OC共需________分钟.
13.某大学的校门如图所示是抛物线形水泥建筑物,大门内侧的地面宽度为8米,两侧距地面4米高处各有一个挂校名横匾用的铁环,两铁环的水平距离为6米,那么校门内侧距地面的高是________米.
三、解答题
14.某汽车出租公司以每辆汽车月租费3000元,100辆汽车可以全部租出.若每辆汽车的月租费每增加50元,则将少租1辆汽车.已知每辆租出的汽车支付月维护费200元,问每月租出多少辆汽车时,该出租公司的月收益最大?最大月收益是多少?
15.如图所示,公园要造圆形的喷水池,在水池中央垂直于水面处安装一个柱子OA,O恰在水面中心,OA=1.25m,由柱子顶端A处的喷头向外喷水,水流在各个方向沿形状相同的抛物线路线落下,为使水流形状较为漂亮,要求设计成水流在离OA距离为1m处达到距水面距离最大,高度2.25m.若不计其他因素,那么水池的半径至少要多少米才能使喷出的水流不致落到池外?
16.某商场将进价40元一个的某种商品按50元一个售出时,每月能卖出500个.商场想了两个方案来增加利润:
方案一:提高价格,但这种商品每个售价涨价1元,销售量就减少10个;
方案二:售价不变,但发资料做广告.已知当这种商品每月的广告费用为m(千元)时,每月销售量将是原销售量的p倍,且p = .
试通过计算,请你判断商场为赚得更大的利润应选择哪种方案?请说明你判断的理由!
17.公司投资750万元,成功研制出一种市场需求量较大的产品,并再投入资金1750万元进行相关生产设备的改进.已知生产过程中,每件产品的成本为60元.在销售过程中发现,当销售单价定为120元时,年销售量为24万件;销售单价每增加10元,年销售量将减少1万件.设销售单价为x(元)(x>120),年销售量为y(万件),第一年年获利(年获利=年销售额﹣生产成本)为z(万元).
(1)求出y与x之间,z与x之间的函数关系式;
(2)该公司能否在第一年收回投资.
18.如图,抛物线y=ax2+bx+c与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于C(0,﹣3).
(1)求抛物线的解析式;
(2)D是y轴正半轴上的点,OD=3,在线段BD上任取一点E(不与B,D重合),经过A,B,E三点的圆交直线BC于点F,
①试说明EF是圆的直径;
②判断△AEF的形状,并说明理由.
四、综合题
19.某商场经营某种品牌的玩具,购进时的单价是40元,根据市场调查:在一段时间内,销售单价是50元时,销售量是600件,而销售单价每涨2元,就会少售出20件玩具.
(1)不妨设该种品牌玩具的销售单价为x元(x>50),请你分别用x的代数式来表示销售量y件和销售该品牌玩具获得利润ω元,并把结果填写在表格中:
销售单价(元)
x
销售量y(件)
________
销售玩具获得利润ω(元)
________
(2)在(1)问条件下,若玩具厂规定该品牌玩具销售单价不低于54元,且商场要完成不少于400件的销售任务,求商场销售该品牌玩具获得的最大利润是多少元?
20.某水果销售店在草莓销售旺季,试销售成本为每千克20元的草莓,规定试销期间销售单价不低于成本单价,也不高于每千克40元,经试销发现,销售量y(千克)与销售单价x(元)符合一次函数关系,如图是y与x的函数关系图象.
(1)求y与x的函数解析式;
(2)设该水果销售店试销草莓获得的利润为W元,求W的最大值.
21.如图,在一次高尔夫球的比赛中,某运动员在原点O处击球,目标是离击球点10米远的球洞,球的飞行路线是一条抛物线,结果球的落地点距离球洞2米,(击球点、落地点、球洞三点共线)球在空中最高处达3.2米.
(1)求表示球飞行的高度y(单位:米)与表示球飞出的水平距离x(单位:米)之间的函数关系式;
(2)当球的飞行高度不低于3米时,求x的取值范围.
答案解析部分
一、单选题
1.【答案】 A
解:由图象可知,点(0,0),(6,0),(3,40)在抛物线上,顶点为(3,40),
设函数解析式为h=a(t﹣3)2+40,
将(0,0)代入得:0=a(0﹣3)2+40,
解得:a= ?409 ,
∴h= ?409 (t﹣3)2+40.
①∵顶点为(3,40),
∴小球抛出3秒时达到最高点,故①正确;
②小球从抛出到落地经过的路程应为该小球从上升到落下的长度,故为40×2=80m,故②正确;
③令h=20,则20= ?409 (t﹣3)2+40,
解得t=3± 322 ,故③错误;
④令t=2,则h= ?409 (2﹣3)2+40= 3209 m,故④错误.
综上,正确的有①②.
故答案为:A.
2.【答案】 C
解:设此函数解析式为: y=ax2 , a≠0 ;
那么 (2,?2) 应在此函数解析式上.
则 ?2=4a
即得 a=?12 ,
那么 y=?12x2 .
当x=3时, y=?12×32=?4.5
∴水面下降(-2)-(-4.5)=2.5(米)
故答案为:C.
3.【答案】 A
解:∵竖直上抛的小球离地面的高度h(米)与时间t(秒)的函数关系式为h=﹣2t2+mt+ 258 ,小球经过 74 秒落地,
∴t= 74 时,h=0,
则0=﹣2×( 74 )2+ 74 m+ 258 ,
解得:m= 127 ,
当t= ?b2a = ?1272×(?2) = 37 时,h最大,
故答案为: 37 .
4.【答案】 D
解:过点A作AD∥BC
∴∠DAC=∠ACB
∵CA平分∠OCB
∴∠OCA=∠ACB
∴∠DCA=∠DAC
∴DA=CD
当x=0时y=3m
∴点C(0,3m)
∴OC=3m,
当y=0时mx2-4mx+3m=0??
∵m≠0
∴x2-4x+3=0
解之:x1=1,x2=3
∴点A(1,0),点B(3,0)
∴OA=1,OB=3.
∵AD∥BC
∴ODOC=OAOB即OD3m=13
解之:OD=m,
∴AD=CD=OC-OD=3m-m=2m,
在Rt△OAD中,
AD2-OD2=OA2
∴(2m)2-m2=12
解之:m1=33 , m2=?33<0(舍去).
故答案为:D.
5.【答案】 C
解:如图,过点C作CE⊥AB于E,?
则四边形ADCE为矩形,设CD=AE=x,∠DCE=∠CEB=90°,?则∠BCE=∠BCD-∠DCE=30°,BC=12-x,
在Rt△CBE中,∵∠CEB=90°,
∴BE=12BC=6?12x
∴AD=CE=3BE=63?32x,AB=AE+BE=x+6?12x=12x+6
∴梯形ABCD面积 S=12(CD+AB)?CE=12(x+12x+6)?(63?32x)=?338x2+33x+183=?3388 (x?4)2+243
∴当x=4时,S最大=24 3 .?
即CD长为4 m时,使梯形储料场ABCD的面积最大为24 3 ?m2。
故答案为:C。
6.【答案】 B
解:如图,
当x+2=8-x时,y有最大值,
即:x=3,y最大=3+2=5.
故答案为:B.
7.【答案】 C
解:方程ax2+bx+c-m=0有实数根,相当于y=ax2+bx+c(a≠0)平移m个单位与x轴有交点,
又∵图象最高点y=3,
∴二次函数最多可以向下平移三个单位,
∴m≤3,
故答案为:C.
8.【答案】 B
解:∵P在直线y=-x+6上,
∴设P坐标为(m,6-m),
连接OQ,OP,由PQ为圆O的切线,得到PQ⊥OQ,
在Rt△OPQ中,根据勾股定理得:OP2=PQ2+OQ2 ,
∴PQ2=m2+(6-m)2-2=2m2-12m+34=2(m-3)2+16,
则当m=3时,切线长PQ的最小值为4.
故答案为:B.
9.【答案】 C
解:设包装盒的高为h(cm),底面边长为a(cm),则a= 2 x,h= 2 (40﹣x),0<x<40.S=4ah=8x(40﹣x)=﹣8(x﹣20)2+3200,∴当x=20cm时,S取最大值.故答案为:C.
二、填空题
10.【答案】 85
解:∵ y=?35x2+65x+1
= ?35(x2?2x?53)
= ?35[(x?1)2?83]
= ?35(x?1)2+85
∴抛物线的最大值为 85 ,
故他能跳过的最大高度为 85 .
11.【答案】 0.4
解:如图,
令P下方的点为H,以AB中点为原点,建立坐标系xOy,则A(1,0),B(-1,O),
设抛物线的方程为y=ax2+bx+c
∴抛物线的对称轴为x=0,则 ?b2a =0,即b=0.
∴y=ax2 +c.
将A(1,0)代入得a+c=0,则c=-a.
∴y=ax2-a.
∵OH=2× 15 × 12 =0.2,则点H的坐标为(-0.2,0)
同理可得:点F的坐标为(-0.6,0).
∴PH=a×(-0.2)2-a=-0.96a
EF=a×(-0.6)2-a=-0.64a.
又∵PQ=EF=1-(-0.96a)=-0.64a
∴1+0.96a=-0.64a.
解得a= ?58 .
∴y= ?58 x2+ 58 .
∴EF=( ?58 )×(-0.6)2+ 58 = 25 .
故答案为:0.4.
12.【答案】 20
解:如图所示:
设在6分钟时到达A点,在14分钟时到达B,
∵6分钟和14分钟时拱梁的高度相同,
∴A,B关于对称轴对称.则从A到B需要8分钟,则从A到D需要4分钟.
∴从O到D需要6+4=10分.
∴从O到C需要2×10=20分.
故答案为:20.
13.【答案】 647
解:建立如图所示的平面直角坐标系,
设抛物线的解析式为 y=ax2+c ,
由题意得:此抛物线的图象经过点 (82,0) 和点 (62,4) ,即点 (4,0) 和点 (3,4) ,
将点 (4,0) 和点 (3,4) 代入得: {16a+c=09a+c=4 ,
解得 {a=?47c=647 ,
则抛物线的解析式为 y=?47x2+647 ,
当 x=0 时, y=647 ,
即校门内侧距地面的高是 647 米,
故答案为: 647 .
三、解答题
14.【答案】 解:设每月租出 x 辆汽车时,该出租公司的月收益最大,月收益为 y 元.
根据题意得: y=[3000+50(100?x)]x?200x ,
即: y=?50x2+7800x .
配方得: y=?50(x?78)2+304200 .
故每月租出78辆汽车时,该出租公司的月收益最大,最大月收益是304200元.
15.【答案】 解:以地面上任一条直线为x轴,OA为y轴建立直角坐标系,
设y=a(x-1)2+2.25,则当x=0时,y=1.25,故a+2.25=1,a=-1.
由y=0得-(x-1)2+2.25=0,得(x-1)2=2.25,解得x1=2.5,x2=-0.5(舍去)
故水池的半径至少要2.5米.
16.【答案】 解:设涨价x元,利润为y元,则
方案一:涨价x元时,该商品每一件利润为:50+x?40,销售量为:500?10x,
∴ y=(50+x?40)(500?10x)=?10x2+400x+5000=?10(x?20)2+9000 ,
∵当x=20时,y最大=9000,
∴方案一的最大利润为9000元;
方案二:该商品售价利润为=(50?40)×500p,广告费用为:1000m元,
∴ y=(50?40)×500p?1000m=?2000m2+9000m=?2000(m?2.25)2+10125 ,
∴方案二的最大利润为10125元;
∴选择方案二能获得更大的利润.
17.【答案】 解:由题意得,
y=24﹣x?12010 , 即y=﹣110x+36,
z=(x﹣60)(﹣110x+36)=﹣110x2+42x﹣2160;
(2)z=﹣110x2+42x﹣2160=﹣110(x﹣210)2+2250,
当x=210时,第一年的年最大利润为2250万元,
∵2250<750+1750,
∴公司不能在第一年收回投资.
18.【答案】 解:(1)∵抛物线y=ax2+bx+c与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于C(0,﹣3),
∴有0=a?b+c0=9a+3b+c?3=c , 解得a=1b=?2c=?3 ,
∴抛物线的解析式为y=x2﹣2x﹣3.
(2)按照题意画出图形,如下图,
①∵B点坐标(3,0)、C点坐标(0,﹣3),
∴OB=OC=3,
∴△BOC为等腰直角三角形,
∴∠CBO=45°,
又∵D是y轴正半轴上的点,OD=3,
∴△BOD为等腰直接三角形,
∴∠OBD=45°,
∠CBD=∠CBO+∠OBD=45°+45°=90°,
即∠FBE=90°,
∴EF是圆的直径.
②∵∠CBO=∠OBD=45°,∠AFE=∠OBD,∠AEF=∠CBO(在同圆中,同弧所对的圆周角相等),
∴∠AEF=∠AFE=45°,
∴∠FAE=90°,AE=AF,
∴△AEF是等腰直角三角形.
四、综合题
19.【答案】 (1)-10x+1100;?10x2+1500x?44000
(2)解:由题得 {x≥54?10x+1100≥400 ,解得: 54≤x≤70 ?
w=?10(x?75)2+12250 ,
∴ x=70 时取最大值,最大值为12000.
答:商场的最大利润为12000元
解:(1)由销售单价每涨1元,就会少售出10件玩具得,
①: y=600?(x?50)×10=1100?10x,
②: w=(1100?10x)(x?40)=?10x2+1500x?44000;
故答案为:① ?10x+1100;②?10x2+1500x?44000;
20.【答案】 (1)解:设y与x的函数关系式为y=kx+b,
根据题意,得: {20k+b=30030k+b=280 ,解得: {k=?2b=340 ,
∴y与x的函数解析式为y=-2x+340(20≤x≤40).
(2)解:由已知得:W=(x-20)(-2x+340)
=-2x2+380x-6800
=-2×(x-95)2+11250,
∵-2<0,
∴当x≤95时,W随x的增大而增大,
∵20≤x≤40,
∴当x=40时,W最大,最大值为-2×(40-95)2+11250=5200元.
21.【答案】 (1)解:抛物线过原点 ,设抛物线解析式为: y=ax2+bx ,
球的落地点距离=10-2=8米,则落地点坐标为(8,0),
∴ 64a+8b=0 ,
∴ 8a+b=0 ,
球在空中最高处达3.2米,
∴ ?b24a=3.2 ,
∴ b2+12.8a=0 ,
∴ {8a+b=0b2+12.8a=0 ,
解得: {a=?0.2b=1.6 ,
∴ y=?0.2x2+1.6x ;
(2)解:当y=3时, ?0.2x2+1.6x=3 ,
整理得: x2?8x+15=0 ,
∴ (x?3)(x?5)=0 ,
∴ x=3 或 x=5 ,
∵ a=?0.2<0 ,抛物线开口向下,球的飞行高度不低于3米应在两根之间,
∴球的飞行高度不低于3米, x的取值范围是 3≤x≤5 .
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
