北师大版八年级数学上册2.3立方根一课一练习题1(Word版,含答案)
文档属性
| 名称 | 北师大版八年级数学上册2.3立方根一课一练习题1(Word版,含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 243.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-02 00:00:00 | ||
图片预览




文档简介
2.3《立方根》习题1
一、填空题
1.下列等式:①=±12,②=﹣2,③=2,④=-,⑤=﹣2;其中正确的有________.只填序号)
2.如果x2=1,那么的值是_____.
3.若是的立方根,则___________.
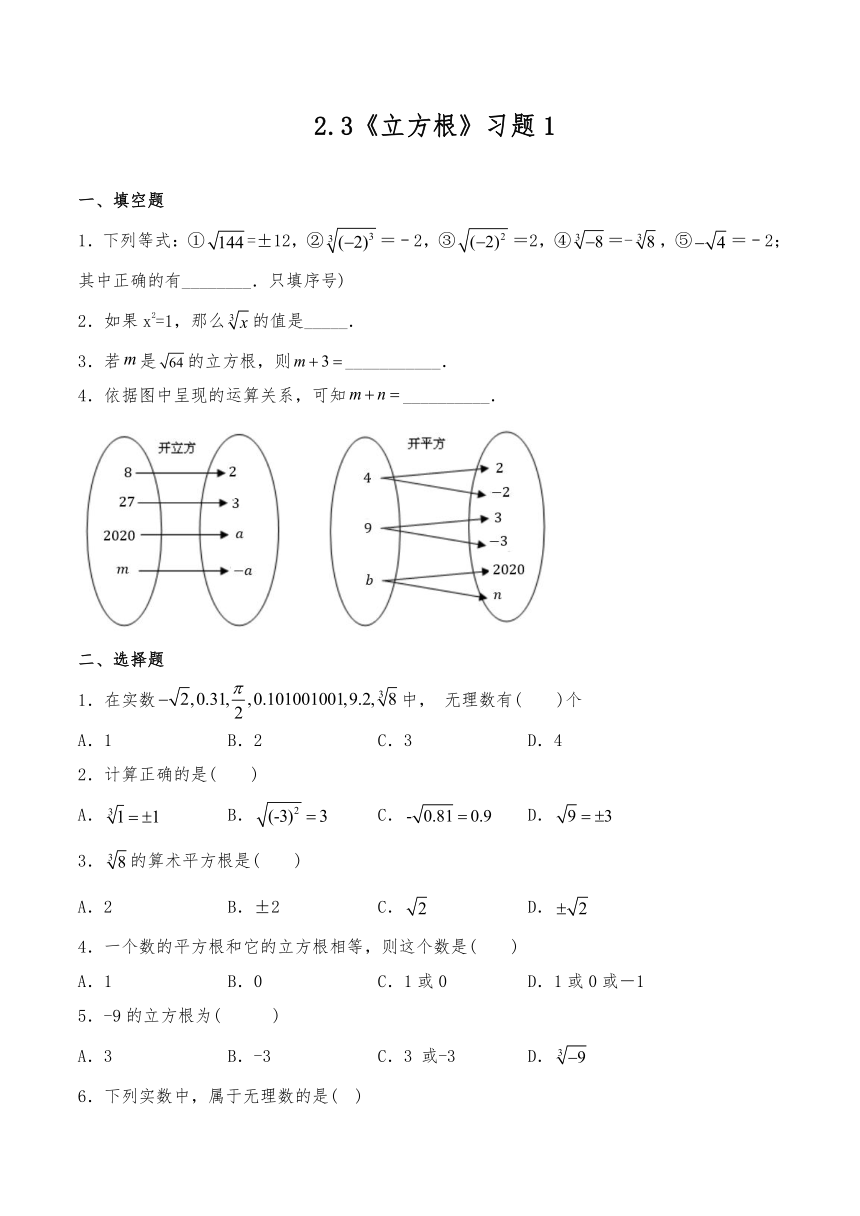
4.依据图中呈现的运算关系,可知__________.
二、选择题
1.在实数中,
无理数有(
)个
A.1
B.2
C.3
D.4
2.计算正确的是( )
A.
B.
C.
D.
3.的算术平方根是( )
A.2
B.±2
C.
D.
4.一个数的平方根和它的立方根相等,则这个数是(
)
A.1
B.0
C.1或0
D.1或0或-1
5.-9的立方根为(
)
A.3
B.-3
C.3
或-3
D.
6.下列实数中,属于无理数的是(
)
A.
B.
C.
D.
7.下列说法错误的是( )
A.3的平方根是
B.﹣1的立方根是﹣1
C.0.1是0.01的一个平方根
D.算术平方根是本身的数只有0和1
8.下列说法:①一个数的平方根一定有两个;②一个正数的平方根一定是它的算术平方根;③负数没有立方根.其中正确的个数有(
)
A.0个
B.1个
C.2个
D.3个
9.下列说法正确的是(
)
A.a的平方根是±
B.a的立方根是
C.的平方根是0.1
D.
10.一个自然数的立方根为a,则下一个自然数的立方根是( )
A.a+1
B.
C.
D.a3+1
11.一个数的算术平方根是2,则这个数的立方根是(
)
A.-
B.
C.
D.±
12.已知一个正数的两个平方根分别是3a+1和a+11,这个数的立方根为(
)
A.4
B.3
C.2
D.0
13.-27的立方根与的平方根之和为(
)
A.6
B.6或-12
C.0或-6
D.0或6
14.小幸学习了在数轴上画出表示无理数的点的方法后,进行以下练习:首先画出数轴,原点为O,在数轴上找到表示数2的点A,然后过点A作AB⊥OA,使AB=3.以点O为圆心,OB为半径作弧,交数轴正半轴于点P,则点P所表示的数介于( )
A.3和3.5之间
B.3.5和4之间
C.4和4.5之间
D.4.5和5之间
三、解答题
1.求下列各式中的的值
(1)
(2)
2.计算:
(1)﹣;
(2)﹣|﹣3|+.
(3)已知a=,b3=﹣1,c=,求a﹣b+c的值.
3.一种长方体的书,长与宽相等,四本同样的书叠在一起成一个正方体,体积为216立方厘米,求这本书的高度.
4.已知某正数的平方根是2a﹣7和a+4,b﹣12的立方根为﹣2.
(1)求a、b的值;
(2)求a+b的平方根.
5.我国数学家华罗庚在一次出国访问途中,看到飞机上邻座的乘客阅读的杂志上有一道智力题:求59319的立方根,华罗庚脱口说出答案,众人十分惊奇,忙问计算的奥妙.你知道他是怎样迅速准确地计算出结果的吗?
下面是小超的探究过程,请补充完整:
(1)求;
①由103=1000,1003=1
000
000,可以确定是
位数;
②由59319的个位上的数是9,可以确定的个位上的数是
;
③如果划去59319后面的三位319得到数59,而33=27,43=64,可以确定的十位上的数是
;
由此求得=
.
(2)已知103823也是一个整数的立方,用类似的方法可以求得=
.
6.某地气象资料表明:当地雷雨持续的时间t(h)可
以用下面的公式来估计:
,其中d(km)是雷雨区域的直径.
(1)如果雷雨区域的直径为6km,那么这场雷雨大约能持续多长时间?
(结果如果有根号,请保留根号)
(2)如果一场雷雨持续了0.9h,那么这场雷雨区域的直径大约是多少?
7.(1)已知2a-1的算术平方根是3,14-3b的立方根2,,求a+2b的平方根;
(2)若2x-4与3x+1是同一个正数的平方根,求x的值.
8.阅读下面的文字后回答问题:
我们知道无理数是无限不循环小数,例如=1.414…,的小数部分我们无法全部出来,但可以用﹣1来表示.
请解答下列问题:
(1)的整数部分是
,小数部分是
.
(2)若的小数部分是a,的整数部分是b,求a(b+)的值.
(3)9﹣的小数部分是a,4+的整数部分是b,求a(b+)的立方根.
答案
一、填空题
1.②③④⑤
2.±1.
3.5.
4.
二、选择题
1.B.2.B.3.C.4.B.5.D.6.B.7.A
8.A.9.B.
10.C.11.B.
12.A
13.C.14.B
三、解答题
1.解:(1)∵;
∴,
∴,
∴;
(2)∵,
∴,
解得:.
2.(1)﹣
;
(2)﹣|﹣3|+
;
(3)
∵a==3,b=-1,c==-2,
∴.
3.解:设书的高为xcm,
由题意得:(4x)3=216,
解得:x=1.5.
答:这本书的高度为1.5cm.
4.解:(1)由题意得,2a?7+a+4=0,
解得:a=1,
b?12=?8,
解得:b=4;
(2)a+b=5,
a+b的平方根为
5.解:(1)①∵103=1000,1003=1
000
000,而1000<59319<100000,
∴10<<100,
因此结果为两位数;
②因为只有9的立方的个位数字才是9,因此结果的个位数字为9,
③33<59<43,因此可以确定的十位上的数是3,
最后得出=39,
故答案为:两,9,3、39;
(2)∵103=1000,1003=1
000
000,而1000<103823<1000000,
∴10<<100,
因此结果为两位数;
只有7的立方的个位数字是3,因此结果的个位数字是7;
如果划去103823后面的三位823得到数103,而43=64,53=125,可以确定的十位数字为4,
于是可得=47;
故答案为:47.
6.解:(1)∵,
∴,
当d=6时,,
即这场雷雨大约能持续h;
(2)当t=0.9时,
即这场雷雨区域的直径大约是9km.
7.解:(1)∵2a-1的算术平方根是3
∴,解得:
又∵14-3b的立方根2
∴,解得:
∴
∴a+2b的平方根是;
(2)∵2x-4与3x+1是同一个正数的平方根
①当2x-4与3x+1相反时:
∴,解得:
②当2x-4与3x+1相等时:
∴,解得:
综上所述:或
8.(1)∵4<<5,
∴的整数部分是4,小数部分是
﹣4,
故答案为:4,﹣4;
(2)∵2<<3,
∴a=﹣2,
∵2<<3,
∴b=2,
∴a(b+)=(﹣2)(2+)=1;
(3)∵9﹣的整数部分是4,
∴9﹣的小数部分:a=9﹣﹣4=5﹣,
4+的整数部分:b=5,
∴a(b+)=(5﹣)(5+)=8,
∴a(b+)的立方根是:2.
一、填空题
1.下列等式:①=±12,②=﹣2,③=2,④=-,⑤=﹣2;其中正确的有________.只填序号)
2.如果x2=1,那么的值是_____.
3.若是的立方根,则___________.
4.依据图中呈现的运算关系,可知__________.
二、选择题
1.在实数中,
无理数有(
)个
A.1
B.2
C.3
D.4
2.计算正确的是( )
A.
B.
C.
D.
3.的算术平方根是( )
A.2
B.±2
C.
D.
4.一个数的平方根和它的立方根相等,则这个数是(
)
A.1
B.0
C.1或0
D.1或0或-1
5.-9的立方根为(
)
A.3
B.-3
C.3
或-3
D.
6.下列实数中,属于无理数的是(
)
A.
B.
C.
D.
7.下列说法错误的是( )
A.3的平方根是
B.﹣1的立方根是﹣1
C.0.1是0.01的一个平方根
D.算术平方根是本身的数只有0和1
8.下列说法:①一个数的平方根一定有两个;②一个正数的平方根一定是它的算术平方根;③负数没有立方根.其中正确的个数有(
)
A.0个
B.1个
C.2个
D.3个
9.下列说法正确的是(
)
A.a的平方根是±
B.a的立方根是
C.的平方根是0.1
D.
10.一个自然数的立方根为a,则下一个自然数的立方根是( )
A.a+1
B.
C.
D.a3+1
11.一个数的算术平方根是2,则这个数的立方根是(
)
A.-
B.
C.
D.±
12.已知一个正数的两个平方根分别是3a+1和a+11,这个数的立方根为(
)
A.4
B.3
C.2
D.0
13.-27的立方根与的平方根之和为(
)
A.6
B.6或-12
C.0或-6
D.0或6
14.小幸学习了在数轴上画出表示无理数的点的方法后,进行以下练习:首先画出数轴,原点为O,在数轴上找到表示数2的点A,然后过点A作AB⊥OA,使AB=3.以点O为圆心,OB为半径作弧,交数轴正半轴于点P,则点P所表示的数介于( )
A.3和3.5之间
B.3.5和4之间
C.4和4.5之间
D.4.5和5之间
三、解答题
1.求下列各式中的的值
(1)
(2)
2.计算:
(1)﹣;
(2)﹣|﹣3|+.
(3)已知a=,b3=﹣1,c=,求a﹣b+c的值.
3.一种长方体的书,长与宽相等,四本同样的书叠在一起成一个正方体,体积为216立方厘米,求这本书的高度.
4.已知某正数的平方根是2a﹣7和a+4,b﹣12的立方根为﹣2.
(1)求a、b的值;
(2)求a+b的平方根.
5.我国数学家华罗庚在一次出国访问途中,看到飞机上邻座的乘客阅读的杂志上有一道智力题:求59319的立方根,华罗庚脱口说出答案,众人十分惊奇,忙问计算的奥妙.你知道他是怎样迅速准确地计算出结果的吗?
下面是小超的探究过程,请补充完整:
(1)求;
①由103=1000,1003=1
000
000,可以确定是
位数;
②由59319的个位上的数是9,可以确定的个位上的数是
;
③如果划去59319后面的三位319得到数59,而33=27,43=64,可以确定的十位上的数是
;
由此求得=
.
(2)已知103823也是一个整数的立方,用类似的方法可以求得=
.
6.某地气象资料表明:当地雷雨持续的时间t(h)可
以用下面的公式来估计:
,其中d(km)是雷雨区域的直径.
(1)如果雷雨区域的直径为6km,那么这场雷雨大约能持续多长时间?
(结果如果有根号,请保留根号)
(2)如果一场雷雨持续了0.9h,那么这场雷雨区域的直径大约是多少?
7.(1)已知2a-1的算术平方根是3,14-3b的立方根2,,求a+2b的平方根;
(2)若2x-4与3x+1是同一个正数的平方根,求x的值.
8.阅读下面的文字后回答问题:
我们知道无理数是无限不循环小数,例如=1.414…,的小数部分我们无法全部出来,但可以用﹣1来表示.
请解答下列问题:
(1)的整数部分是
,小数部分是
.
(2)若的小数部分是a,的整数部分是b,求a(b+)的值.
(3)9﹣的小数部分是a,4+的整数部分是b,求a(b+)的立方根.
答案
一、填空题
1.②③④⑤
2.±1.
3.5.
4.
二、选择题
1.B.2.B.3.C.4.B.5.D.6.B.7.A
8.A.9.B.
10.C.11.B.
12.A
13.C.14.B
三、解答题
1.解:(1)∵;
∴,
∴,
∴;
(2)∵,
∴,
解得:.
2.(1)﹣
;
(2)﹣|﹣3|+
;
(3)
∵a==3,b=-1,c==-2,
∴.
3.解:设书的高为xcm,
由题意得:(4x)3=216,
解得:x=1.5.
答:这本书的高度为1.5cm.
4.解:(1)由题意得,2a?7+a+4=0,
解得:a=1,
b?12=?8,
解得:b=4;
(2)a+b=5,
a+b的平方根为
5.解:(1)①∵103=1000,1003=1
000
000,而1000<59319<100000,
∴10<<100,
因此结果为两位数;
②因为只有9的立方的个位数字才是9,因此结果的个位数字为9,
③33<59<43,因此可以确定的十位上的数是3,
最后得出=39,
故答案为:两,9,3、39;
(2)∵103=1000,1003=1
000
000,而1000<103823<1000000,
∴10<<100,
因此结果为两位数;
只有7的立方的个位数字是3,因此结果的个位数字是7;
如果划去103823后面的三位823得到数103,而43=64,53=125,可以确定的十位数字为4,
于是可得=47;
故答案为:47.
6.解:(1)∵,
∴,
当d=6时,,
即这场雷雨大约能持续h;
(2)当t=0.9时,
即这场雷雨区域的直径大约是9km.
7.解:(1)∵2a-1的算术平方根是3
∴,解得:
又∵14-3b的立方根2
∴,解得:
∴
∴a+2b的平方根是;
(2)∵2x-4与3x+1是同一个正数的平方根
①当2x-4与3x+1相反时:
∴,解得:
②当2x-4与3x+1相等时:
∴,解得:
综上所述:或
8.(1)∵4<<5,
∴的整数部分是4,小数部分是
﹣4,
故答案为:4,﹣4;
(2)∵2<<3,
∴a=﹣2,
∵2<<3,
∴b=2,
∴a(b+)=(﹣2)(2+)=1;
(3)∵9﹣的整数部分是4,
∴9﹣的小数部分:a=9﹣﹣4=5﹣,
4+的整数部分:b=5,
∴a(b+)=(5﹣)(5+)=8,
∴a(b+)的立方根是:2.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
