三角形中的边角关系
图片预览






文档简介
(共28张PPT)
亳州四中吴拉连
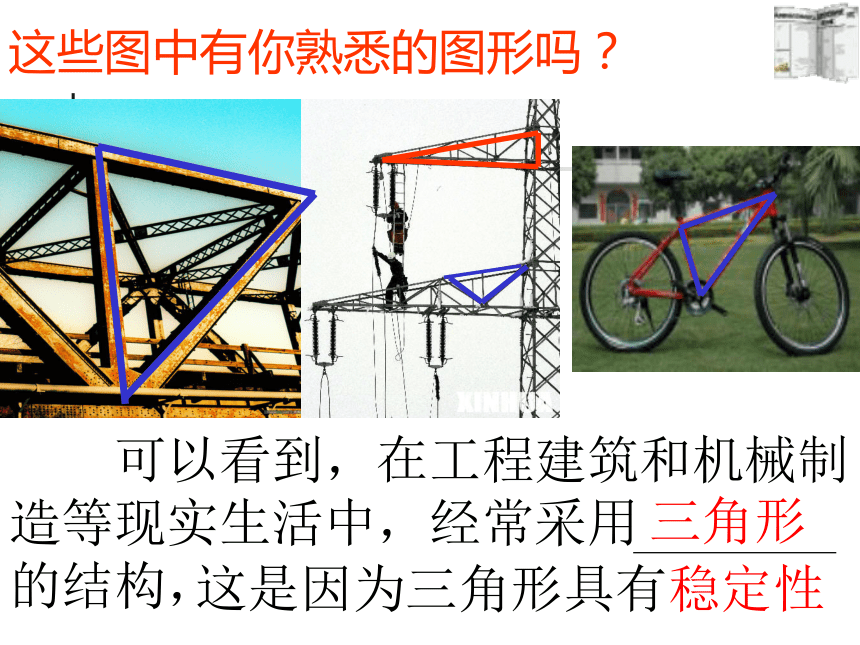
这些图中有你熟悉的图形吗?
可以看到,在工程建筑和机械制造等现实生活中,经常采用 的结构,
三角形
这是因为三角形具有稳定性
第一课时
请同学们对照提纲阅读教科书第68页
阅读提纲:
1.知道三角形的定义,会用几何符号表示一个三角形
2.知道三角形的顶点、角、边等概念,并会用几何符号表示。
3.会把三角形按边进行分类,知道每类三角形的特征
4.知道等腰三角形的腰、底边、顶角、底角等概念。
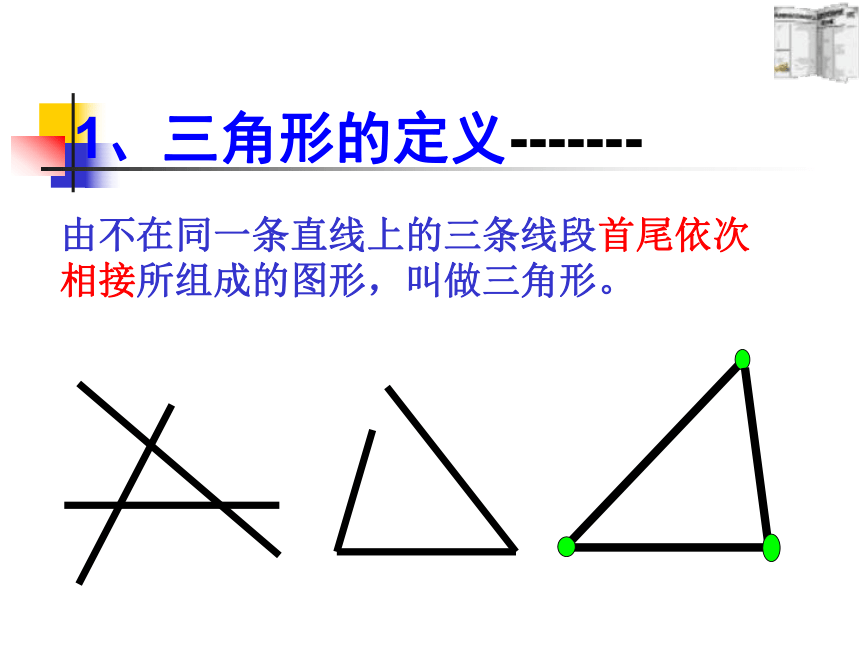
1、三角形的定义-------
由不在同一条直线上的三条线段首尾依次相接所组成的图形,叫做三角形。
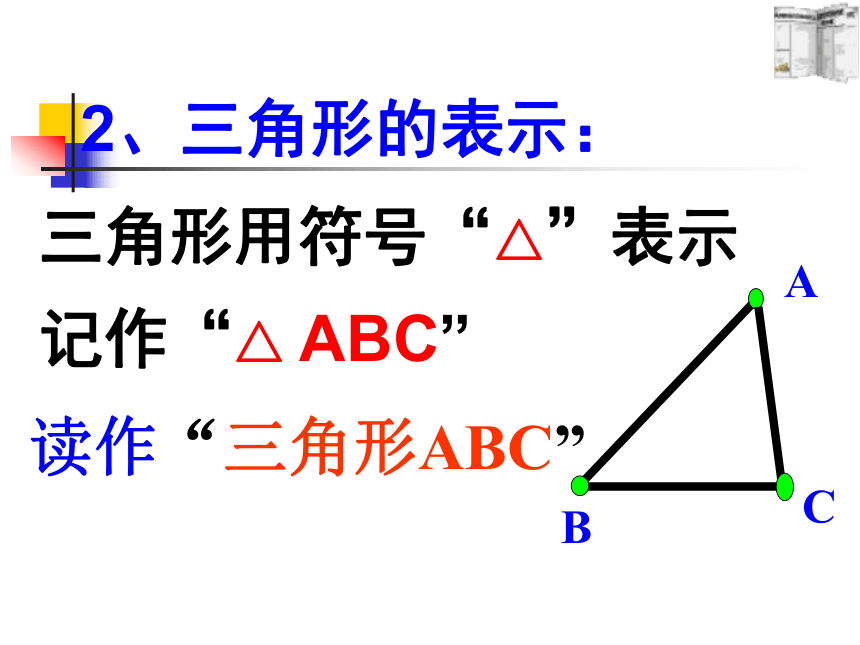
2、三角形的表示:
三角形用符号“△”表示
记作“△ ABC”
B
C
A
读作“三角形ABC”
练习:用符号表示图中的各个三角形.
A
D
B
E
C
△ ABE
△ CDE
△ BCE
△ ABC
△ BCD
三角形相邻两边的公共端点叫做三角形的顶点。
如图,三角形ABC有 个顶点, 它们分别是 。
3、三角形的顶点
A
B
C
三角形的形状、大小和位置由它的 确定。
A、B、C
三个顶点
3
4、三角形的角:
三角形相邻两边所组成的角叫做三角形的内角,简称三角形的角。
如图,三角形ABC有 个角,它们分别是
∠A、∠B、∠C
⌒
⌒
⌒
3
B
C
A
组成三角形的三条线 段叫做三角形的边。
如图,三角形ABC有 条边,它们分别是______________。
5、三角形的边
A
B
C
△ABC的三边,有时也用a、b、c来表示.
AB、
△ABC的三边还有其他表示方法吗?
一般的顶点A所对的边记作a,
3
顶点B所对的边记作b,
顶点C所对的边记作c
AC、
BC
观察:下列每个三角形中,三边长短有何关系?
不等边三角形
等腰三角形
等边三角形
三条边各不相等的三角形叫做不等边三角形 .
有两条边相等的三角形叫做等腰三角形,其中相等的两边都叫做腰,另外一边叫做底边,两腰的夹角叫做顶角,腰和底边的夹角叫做底角
三条边都相等的三角形叫做等边三角形.
等边三角形是等腰三角形吗?
腰
腰
底边
⌒
⌒
⌒
顶角
底角
底角
三角形
按边分类
不等边三角形
等腰三角形
于是我们可以把三角形按照三边情况进行分类
两边相等的等腰三角形
等边三角形
(三边都相等的等腰三角形)
(1)如果腰长是底边长的2倍,求各边长.
答:此三角形的各边长分别是7.2cm、7.2cm、3.6cm
已知:等腰三角形中,周长是18cm
解:
设底边长为xcm,则腰为2xcm,根据题意得
2x+2x+x=18
解得:
x=3.6
7.2
∴腰长2x=
如图,在△ABC中,假设有一只蚂蚁,要从顶点B出发,沿三角形的边爬到顶点C,它有几条路线可选择?哪条路线最短?为什么?
B
C
A
因为“两点之间,线段最短”。
解:有 条路线可选择:
①从B A C
即: AB+AC
②从B C
即: 线段BC
长
短
两
能用不等式表示两条路线的关系吗
B
C
A
AB+AC>BC
同理:
三角形任何两边的和大于第三边!
思考:三角形的三边有怎样的关系
两条路线的关系用不等式表示为:
BC+AC>AB
AB+BC>AC,
AB+AC>BC
你能根据上面的结论,利用不等式的性质,加以说明三角形中任意两边的差与第三边的大小关系吗
三角形任何两边的差小于第三边!
交流:
三角形任何两边的和大于第三边!
AB+BC>AC
BC+AC>AB
1.某村庄和小学分别位于两条交叉的大路边(如图)。可是,每年冬天麦田弄不好就会走出一条小路来。你说小学生为什么会这样走呢?
村庄
学校
麦
田
三角形任何两边的和大于第三边!
2. 用长度分别为4cm、5cm、6cm、10cm的四根木棒,取其中三根搭成三角形。哪些能,哪些不能?你能搭成几个三角形?
①4cm、5cm、6cm
②4cm、5cm、10cm
③4cm、6cm、10cm
④5cm、6cm、10cm
不能
能
不能
能
判断三条线段能否组成三角形,是否一定要检验三条线段中任何两条的和都大于第三条?根据你刚才解题经验,有没有更简便的判断方法?
若两条短线段之和大于最长线段,则能构成三角形;
若不满足,则不能构成三角形
解题技巧:
(2)如果一边长为4cm,求另两边长.
已知:等腰三角形中,周长是18cm
解:
若底边长为4cm,设腰长为xcm,则有
2x+4=18
解得:x =7
若一条腰长为4cm,设底边长为xcm,则有
解得:x =10
因为4+4<10,
所以,以4cm为一腰不能构成三角形
所以,三角形的另两边长都是7cm
“一边长”是指哪边长?底边还是腰?
所以三角形的另两边长是7cm、 7cm或4cm、10cm
(7,7,4)
(4,4,10)
有人说,姚明步子大,一步能走3米多,你相信吗?说说你的理由!
考考你!
大姚的腿到底有多长呢?
由三角形三边的关系得,此人两腿的长度和要超过3米
噢,我懂了!
哇噻!他单腿超过1.5米,腿真长!
小颖要制作一个三角形木架,现有两根长度为8cm和5cm的木棒,如果要求第三根木棒的长度是偶数,小颖有几种选法?第三根的长度可以是多少?
解:设第三根木棒的长度是X cm.则
根据三角形任何两边的和大于第三边,则:8+5>X
根据三角形任何两边的差小于第三边,则:8-5<X
噢!我知道:
两边之差<第三边<两边之和 即:8-5<X<8+5
是小于13的偶数
是大于3的偶数
小颖要制作一个三角形木架,现有两根长度为8cm和5cm的木棒,如果要求第三根木棒的长度是偶数,小颖有几种选法?第三根的长度可以是多少?
∴小颖有5种选法。
第三根木棒的长度可以是:4cm,6cm,8cm,10cm,12cm
解:设第三根木棒的长度是X cm.则
3∵X是偶数
通过本节课的学习,你有哪些收获?
1.三角形的概念
2.三角形的三要素
3.三角形的表示方法
4.三角形按边分类
5.三角形三边之间的关系
P70
习题14.1
1、2、3
亳州四中吴拉连
这些图中有你熟悉的图形吗?
可以看到,在工程建筑和机械制造等现实生活中,经常采用 的结构,
三角形
这是因为三角形具有稳定性
第一课时
请同学们对照提纲阅读教科书第68页
阅读提纲:
1.知道三角形的定义,会用几何符号表示一个三角形
2.知道三角形的顶点、角、边等概念,并会用几何符号表示。
3.会把三角形按边进行分类,知道每类三角形的特征
4.知道等腰三角形的腰、底边、顶角、底角等概念。
1、三角形的定义-------
由不在同一条直线上的三条线段首尾依次相接所组成的图形,叫做三角形。
2、三角形的表示:
三角形用符号“△”表示
记作“△ ABC”
B
C
A
读作“三角形ABC”
练习:用符号表示图中的各个三角形.
A
D
B
E
C
△ ABE
△ CDE
△ BCE
△ ABC
△ BCD
三角形相邻两边的公共端点叫做三角形的顶点。
如图,三角形ABC有 个顶点, 它们分别是 。
3、三角形的顶点
A
B
C
三角形的形状、大小和位置由它的 确定。
A、B、C
三个顶点
3
4、三角形的角:
三角形相邻两边所组成的角叫做三角形的内角,简称三角形的角。
如图,三角形ABC有 个角,它们分别是
∠A、∠B、∠C
⌒
⌒
⌒
3
B
C
A
组成三角形的三条线 段叫做三角形的边。
如图,三角形ABC有 条边,它们分别是______________。
5、三角形的边
A
B
C
△ABC的三边,有时也用a、b、c来表示.
AB、
△ABC的三边还有其他表示方法吗?
一般的顶点A所对的边记作a,
3
顶点B所对的边记作b,
顶点C所对的边记作c
AC、
BC
观察:下列每个三角形中,三边长短有何关系?
不等边三角形
等腰三角形
等边三角形
三条边各不相等的三角形叫做不等边三角形 .
有两条边相等的三角形叫做等腰三角形,其中相等的两边都叫做腰,另外一边叫做底边,两腰的夹角叫做顶角,腰和底边的夹角叫做底角
三条边都相等的三角形叫做等边三角形.
等边三角形是等腰三角形吗?
腰
腰
底边
⌒
⌒
⌒
顶角
底角
底角
三角形
按边分类
不等边三角形
等腰三角形
于是我们可以把三角形按照三边情况进行分类
两边相等的等腰三角形
等边三角形
(三边都相等的等腰三角形)
(1)如果腰长是底边长的2倍,求各边长.
答:此三角形的各边长分别是7.2cm、7.2cm、3.6cm
已知:等腰三角形中,周长是18cm
解:
设底边长为xcm,则腰为2xcm,根据题意得
2x+2x+x=18
解得:
x=3.6
7.2
∴腰长2x=
如图,在△ABC中,假设有一只蚂蚁,要从顶点B出发,沿三角形的边爬到顶点C,它有几条路线可选择?哪条路线最短?为什么?
B
C
A
因为“两点之间,线段最短”。
解:有 条路线可选择:
①从B A C
即: AB+AC
②从B C
即: 线段BC
长
短
两
能用不等式表示两条路线的关系吗
B
C
A
AB+AC>BC
同理:
三角形任何两边的和大于第三边!
思考:三角形的三边有怎样的关系
两条路线的关系用不等式表示为:
BC+AC>AB
AB+BC>AC,
AB+AC>BC
你能根据上面的结论,利用不等式的性质,加以说明三角形中任意两边的差与第三边的大小关系吗
三角形任何两边的差小于第三边!
交流:
三角形任何两边的和大于第三边!
AB+BC>AC
BC+AC>AB
1.某村庄和小学分别位于两条交叉的大路边(如图)。可是,每年冬天麦田弄不好就会走出一条小路来。你说小学生为什么会这样走呢?
村庄
学校
麦
田
三角形任何两边的和大于第三边!
2. 用长度分别为4cm、5cm、6cm、10cm的四根木棒,取其中三根搭成三角形。哪些能,哪些不能?你能搭成几个三角形?
①4cm、5cm、6cm
②4cm、5cm、10cm
③4cm、6cm、10cm
④5cm、6cm、10cm
不能
能
不能
能
判断三条线段能否组成三角形,是否一定要检验三条线段中任何两条的和都大于第三条?根据你刚才解题经验,有没有更简便的判断方法?
若两条短线段之和大于最长线段,则能构成三角形;
若不满足,则不能构成三角形
解题技巧:
(2)如果一边长为4cm,求另两边长.
已知:等腰三角形中,周长是18cm
解:
若底边长为4cm,设腰长为xcm,则有
2x+4=18
解得:x =7
若一条腰长为4cm,设底边长为xcm,则有
解得:x =10
因为4+4<10,
所以,以4cm为一腰不能构成三角形
所以,三角形的另两边长都是7cm
“一边长”是指哪边长?底边还是腰?
所以三角形的另两边长是7cm、 7cm或4cm、10cm
(7,7,4)
(4,4,10)
有人说,姚明步子大,一步能走3米多,你相信吗?说说你的理由!
考考你!
大姚的腿到底有多长呢?
由三角形三边的关系得,此人两腿的长度和要超过3米
噢,我懂了!
哇噻!他单腿超过1.5米,腿真长!
小颖要制作一个三角形木架,现有两根长度为8cm和5cm的木棒,如果要求第三根木棒的长度是偶数,小颖有几种选法?第三根的长度可以是多少?
解:设第三根木棒的长度是X cm.则
根据三角形任何两边的和大于第三边,则:8+5>X
根据三角形任何两边的差小于第三边,则:8-5<X
噢!我知道:
两边之差<第三边<两边之和 即:8-5<X<8+5
是小于13的偶数
是大于3的偶数
小颖要制作一个三角形木架,现有两根长度为8cm和5cm的木棒,如果要求第三根木棒的长度是偶数,小颖有几种选法?第三根的长度可以是多少?
∴小颖有5种选法。
第三根木棒的长度可以是:4cm,6cm,8cm,10cm,12cm
解:设第三根木棒的长度是X cm.则
3
通过本节课的学习,你有哪些收获?
1.三角形的概念
2.三角形的三要素
3.三角形的表示方法
4.三角形按边分类
5.三角形三边之间的关系
P70
习题14.1
1、2、3
