一次函数复习课件

(共26张PPT)
第25章一次函数
（章末复习）
25章 一次函数
（章末复习课）
复习目标
１.梳理本章知识脉络，加强知识点的巩固和理解．
２.进一步学会函数的研究方法，提高解题的灵活性．
３.对综合性题目，会合理使用数学思想方法探究解决．
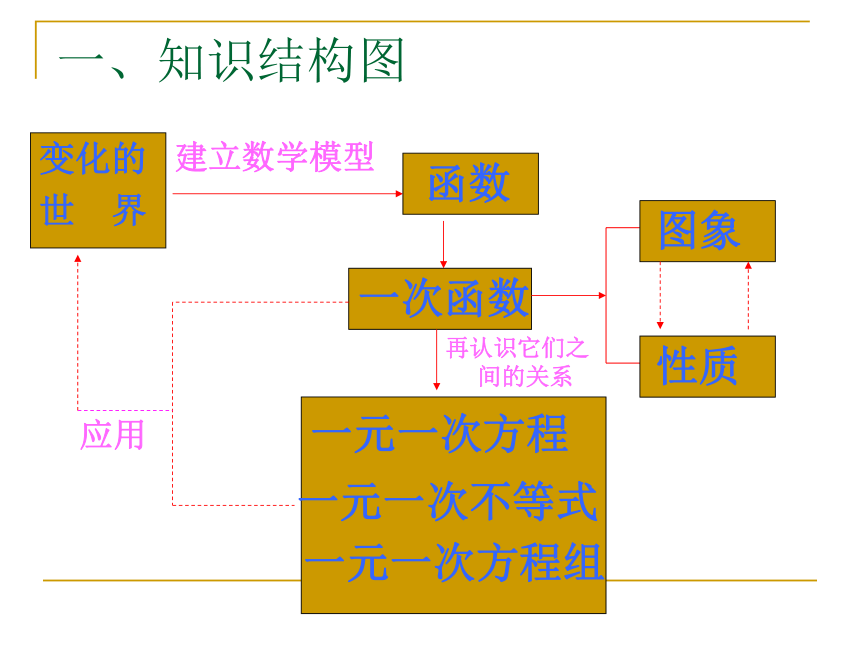
一、知识结构图
变化的
世　界
函数
一次函数
图象
性质
一元一次方程
一元一次不等式
一元一次方程组
再认识它们之间的关系
建立数学模型
应用
二、基本知识点（21章）
1. 叫变量，
叫常量.
2.函数定义：
在一个变化过程中数值发生变化的量
数值始终不变的量
在一个变化过程中，如果有两个变量x与y，并且对于x的每一个确定的值，y都有唯一确定的值与其对应，那么我们就说x是自变量，y是x的函数.
回顾 小结
3.函数的图象：对于一个函数，如果把自变量与函数的每对对应值分别作为点的横坐标和纵坐标，那么坐标平面内由这些点组成的图形，就是这个函数的图象。
列表法，
表达式（解析式）法，
图象法.
4.函数的三种表示方法：
5、自变量的取值范围
（1）分母不为0，（2）开偶次方的被开方数大于或等于0，（3）使实际问题有意义。
x
y
o
.
.
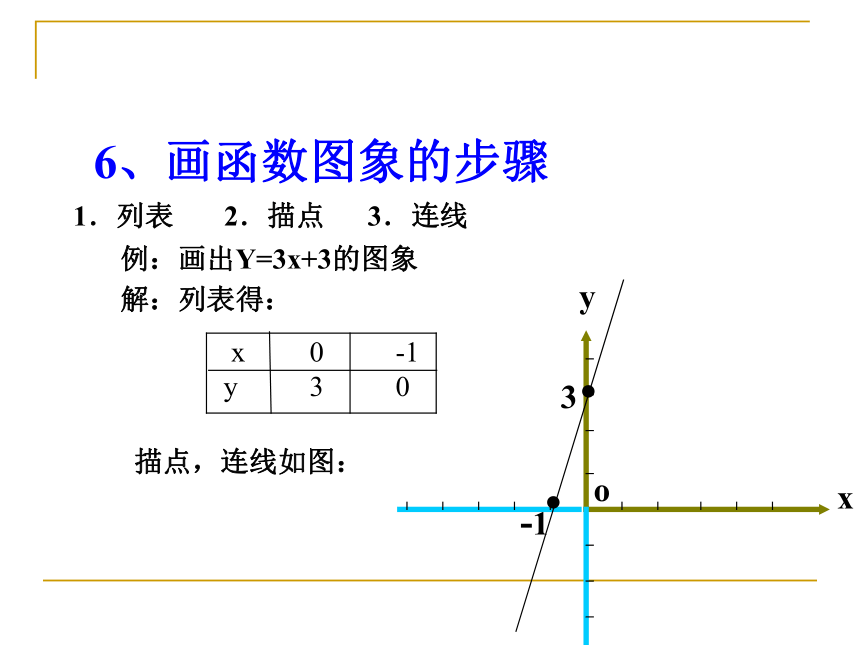
6、画函数图象的步骤
1．列表 2．描点 3．连线
例：画出Y=3x+3的图象
x 0 -1
y 3 0
描点，连线如图：
解：列表得：
3
-1
练习：求下列函数中自变量x的取值范围
（1）y= x（x+3）； （2）y=
（3）y= （4）y=
（5）y=
解：（1）全体实数；
（2）
；
（3）
;
（4）
；
（5）
.
三、知识要点：（25章）
　　1、一次函数的概念：函数y=_______(k、b为常数，k______)叫做一次函数。当b_____时，函数y=____(k____)叫做正比例函数。
kx ＋b
≠０
=０
≠０
kx
★理解一次函数概念应注意下面两点：
　　⑴、表达式中自变量x的次数是___次，⑵、其系数_____。
1
K≠0
　　2、正比例函数y=kx(k≠0)的图象是过点（_____），(______)的_________。
　　 3、一次函数y=kx+b(k≠0)的图象是过点（0，___),（____，0)的__________。
0，0
1，k
一条直线
b
一条直线
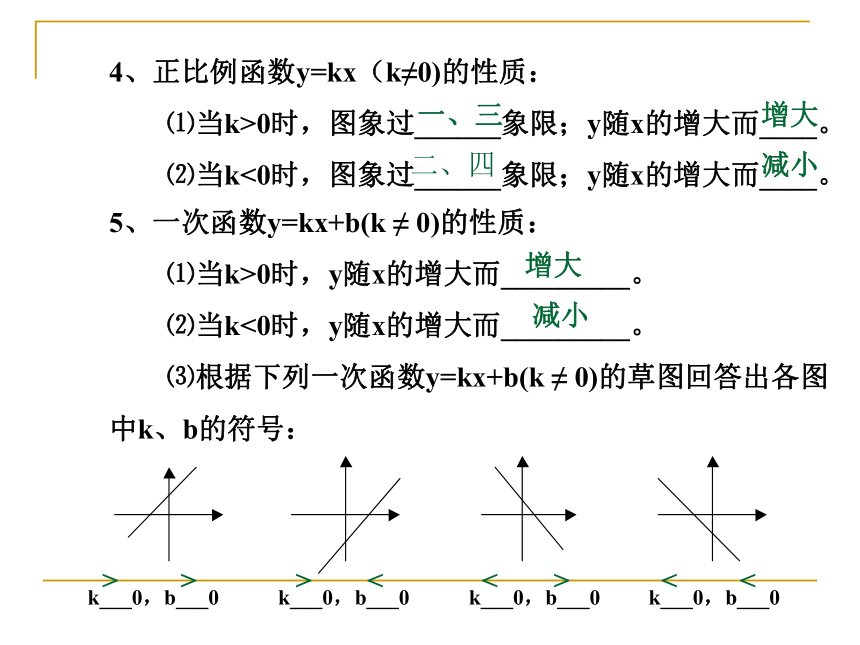
4、正比例函数y=kx（k≠0)的性质：
　　⑴当k>0时，图象过______象限；y随x的增大而____。
　　⑵当k<0时，图象过______象限；y随x的增大而____。
一、三
增大
二、四
减小
5、一次函数y=kx+b(k ≠ 0)的性质：
　　⑴当k>0时，y随x的增大而_________。
　　⑵当k<0时，y随x的增大而_________。
　　⑶根据下列一次函数y=kx+b(k ≠ 0)的草图回答出各图
中k、b的符号：
增大
减小
k___0，b___0 k___0，b___0 k___0，b___0 k___0，b___0
<
<
>
<
<
>
>
>
6、正比例函数和一次函数的比较
正比
例函
数
一次函数
y=kx+b
(k≠0)
当b=0时,一次函数变为正比例函数。也就是说;正比例函数是一次函数的特殊情况
(0,0)
(1,k)
(- ,0)
(0,b)
k>0
一.三
二.四
一.二.三
一.三.四
一.二.四
二.三.四
当k>0,
Y随x的增大而增大.
当k<0,
Y随x的增大而减小.
y=kx (k≠0)
函数 解析式 关系 图象画法 k 、b
符号 草图 所过
象限 性质
k<0
k>0
b>0
k>0
b<0
k<0
b>0
k<0
b<0
y=kx+b 示意图 直线经过的象限 性质
k>0 b=0
b>0
b<0
6.一次函数的图象及性质（K＞0）
x
y
o
x
y
o
x
y
o
一、三
一、二、三
一、三、四
图象从左向右上升即y随 x 的增大而增大
6.一次函数的图象及性质（K ＜ 0）
y=kx+b 示意图 直线经过的象限 性质
k<0 b=0
b>0
b<0
x
y
o
x
y
o
x
y
o
二、四
一、二、四
二、三、四
图象从左向右下降即y随 x 的增大而减小
回顾 小结
7.两函数图像（直线）的位置关系
若直线l1和l2的表达式为y=k1X+b1和y=k2X+b2，它们的位置关系可由其系数确定：
k1 ≠k2
＜
＞
k1 ＝k2
＜
＞
b1 ≠b2
k1 ＝k2
＜
＞
b1 ＝b2
l1和l2相交（ l1和l2有且只有一个交点）
l1和l2平行（ l1和l2没有交点）
l1和l2重合
8.一次函数与方程(组)、不等式之间的完美结合
一次函数
y=kx+b(k≠0)
从数的角度
从形的角度
解一元一次方程
kx+b=0
一次函数
y=kx+b
解一元一次不等式
kx+b>0或kx+b<0
当y=0时
相应的自变量的值
当y>0 或y<0时
自变量相应的取值范围
一次函数与x轴
交点的横坐标
图象在 x 轴的上
方(或下方)的点
的横坐标的集合
两个一次函数
解二元一次方程组
两个一次函数
自变量为何值时
两个函数值相等
以及这时函数值
是多少
两条直线的
交点坐标
解：一次函数当x=1时，y=5。且它的图象与x轴交点
是（６，０）。由题意得
解得
∴一次函数的解析式为　y= - x+6。
点评：用待定系数法求一次函数y=kx+b的解析式，可由已知条件给出的两对x、y的值，列出关于k、b的二元一次方程组。由此求出k、b的值，就可以得到所求的一次函数的解析式。
例1、已知一次函数y=kx+b(k≠0)，当x=1时，y=5，且
它的图象与x轴交点的横坐标是６，求这个一次函数的
解析式。
　例2　柴油机在工作时油箱中的余油量Q(千克）
与工作时间t（小时）成一次函数关系，当工作开始时
油箱中有油40千克，工作3.5小时后，油箱中余油22.5
千克(1)写出余油量Q与时间t的函数关系式；（2）画出
这个函数的图象。
解：（１）设一次函数Ｑ＝kt＋b。
解得
解析式为：Q＝－５t+40　　(0≤t≤8)
把t=0，Q=40；t=3.5，Q=22.5分别代入上式，得
（２）、
点评：（1）求出函数关系式时，
必须找出自变量的取值范围。
（2）画函数图象时，应
根据函数自变量的取值范围来
确定图象的范围。
20
40
8
0
t (小时)
Q (千克）
图象是包括
两端点的线段
.
.
A
B
t 0 8
Q 40 0
例3、已知一次函数y= – 2x – 1与x轴、y轴分别交于Ａ、
求Ｓ AOB。
Ｂ两点，
y
o
A
B
x
解： y= – 2x – 1 与x轴
相交于A点,
– 2x – 1=0
x= –
A( – ，0）。
y= – 2x – 1 与y轴交于
B(0 ， – 1)点，
又
且OA OB，OA=| – | = ，OB=| – 1|=1，
(– ,0)
(0, – 1)
Ｓ AOB = OA OB = .1= 。
注意：平面直角坐标系中，线段的长度为正，须给坐标
加绝对值。如，OA=| – | = ，OB=| – 1|=1。
例4已知：函数y = (m+1) x+2 m﹣6
（1）若函数图象过（﹣1 ，2），求此函数的解析式。
（2）若函数图象与直线 y = 2 x + 5 平行，求其函数的解析式。
（3）求满足（2）条件的直线与此同时y = ﹣3 x + 1 的交点
并求这两条直线 与y 轴所围成的三角形面积
解：（1）由题意:
2=﹣(m+1）+2m﹣6
解得 m = 9
∴ y = 10x+12
(2) 由题意，m +1= 2
解得 m = 1
∴ y = 2x﹣4
(3) 由题意得
解得: x =1 , y = ﹣2
∴ 这两直线的交点是（1 ，﹣2）
y = 2x﹣4 与y 轴交于( 0 , 4 )
y = ﹣3x + 1与y 轴交于( 0 , 1）
●
x
y
o
1
1
﹣4
(1, ﹣2)
S△=
-2
利用数学模型解决实际问题
例5.某商场文具部的某种笔售价25元，练习本每本售价5元。该商场为了促销制定了两种优惠方案供顾客选择。甲：买一支笔赠送一本练习本。乙：按购买金额打九折付款。某校欲购这种笔10支，练习本x（x ≥10)本，如何选择方案购买呢？
解：甲、乙两种方案的实际金额y元与练习本x本之间的关系式是：
y甲=(x-10)××5+25×10=5x+200 (x ≥10)
y乙=(10×25+5x) ×0.9=4.5x+225 (x ≥10)
解方程组
y=5x+200
y=4.5x+225
得
x=50
y=450
o
x
y
10
50
200
由图象可以得出同样结果
当10 ≤ x<50时，y甲当x=50时，y甲=y乙
当x>50时，y甲>y乙
所以我的建议为：……
练习：1.下列函数关系式中，那些是一次函数？
哪些是正比例函数？
（1）y= - x - 4
（2）y=x2
（3）y=2πx
（4）y=
1
——
x
(5)y= (6)y=
(7)y=5x-3 (8)y=6x2-2x-1
2、填空题:
　　(1)、直线y=－　x+1与x轴的交点坐标为（_______），
与Y轴的交点坐标为（_______）。
　　(2)、如果一次函数y=kx-3k+6的图象经过原点，那么
k的值为_________。
　　(3)、已知y-1与x成正比例，且x=－2时，y=4，那么y与
x之间的函数关系式为_________________。
2，0
0，1
k=2
　2、一次函数y=ax+b与y=ax+c(a>0)在同一坐标系中的图象可能是（　 　）
x
y
o
x
y
o
x
y
o
x
y
o
A
B
C
D
1.已知一次函数y=kx+b,y随着x的增大而减小,且kb<0,则在直角坐标系内它的大致图象是( 　)
　(A) 　　　　　(B) 　（C） 　　（D）
A
图象辨析
A
3、如图，已知一次函数y=kx+b的图像,当x<0 ，y的取值范围是（ ）
A.y>0 B.y<0
C.-2.
4、一次函数y=(m-4)x-1和y=(m+2)x+(m2-3)的图像与y轴分别交于P，Q两点，若P、Q两点关于x轴对称，则
m= 。
2
D
5、已知函数y=-x+2.当-11≤y<3
练习； 小星以2米/秒的速度起跑后，先匀速跑5秒，然后突然把速度提高4米/秒，又匀速跑5秒。试写出这段时间里他的跑步路程s（单位：米）随跑步时间x（单位：秒）变化的函数关系式，并画出函数图象。
解:依题意得
{
s=2x
(0≤x≤5)
s=10+6(x-5)
(510
0
s(米)
5
0
x(秒)
①
40
10
s(米)
10
5
x(秒)
②
x(秒）
s(米)
o
·
·
·
·
5
10
10
40
·
·
·
s=2x (0≤x≤5)
s=10+6(x-5) (5