用坐标表示轴对称
图片预览




文档简介
(共31张PPT)
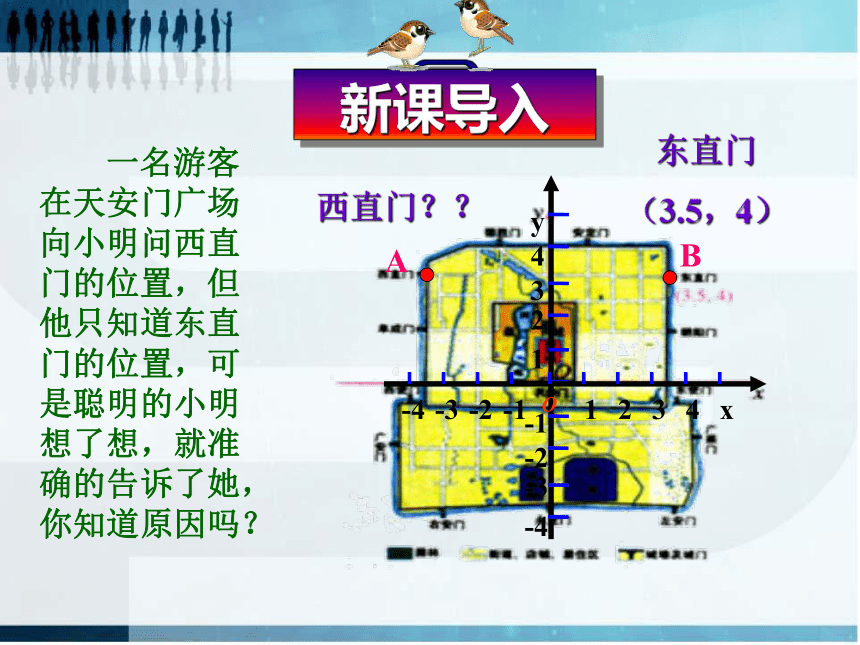
一名游客在天安门广场向小明问西直门的位置,但他只知道东直门的位置,可是聪明的小明想了想,就准确的告诉了她,你知道原因吗?
东直门
(3.5,4)
西直门??
3
1
4
2
y
-2
-4
-1
-3
O
1
2
3
4
x
-4
-3
-2
-1
A
B
新课导入
知识与能力
教学目标
1.能在平面直角坐标系中画出点关于坐标轴对称的点;
2.掌握在平面直角坐标系中,关于x轴和y轴对称点的坐标特点,并能运用它解决简单的问题;
3.能在平面直角坐标系中画出一些简单的关于x轴和y轴的对称图形.
在找关于坐标轴对称的点的坐标之间规律并检验其正确性的过程中,培养语言表达能力、观察能力、归纳能力,养成良好的科学研究方法.
过程与方法
情感态度与价值观
在找点,绘图的过程中体验数形结合思想,体验学习的乐趣.
重点
难点
教学重难点
用坐标表示点关于坐标轴对称的点的坐标.
利用转化的思想,确定能代表轴对称图形的关键点.
·
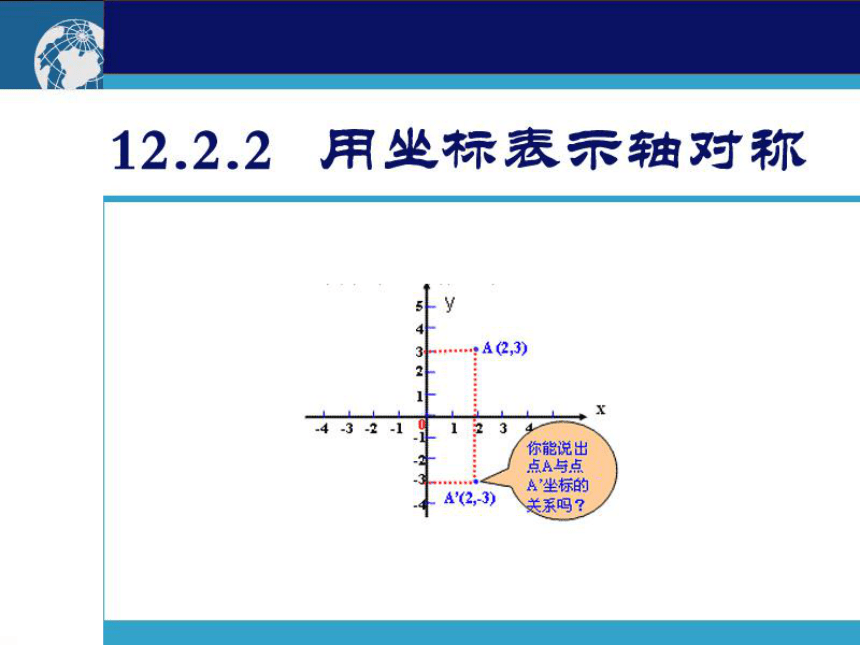
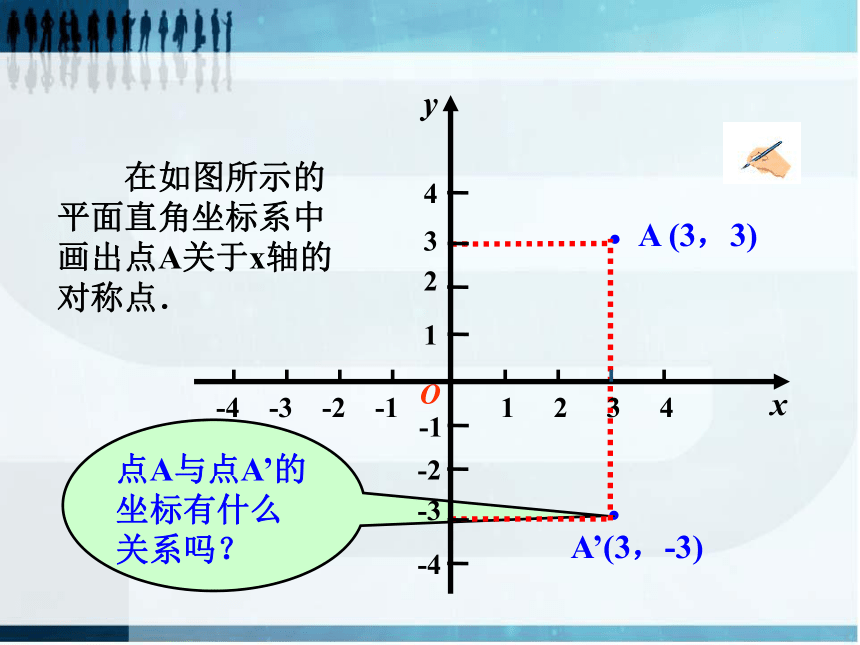
A (3,3)
·
A’(3,-3)
点A与点A’的坐标有什么关系吗?
在如图所示的平面直角坐标系中画出点A关于x轴的对称点.
3
1
4
2
-2
-4
-1
-3
O
1
2
3
4
-4
-3
-2
-1
x
y
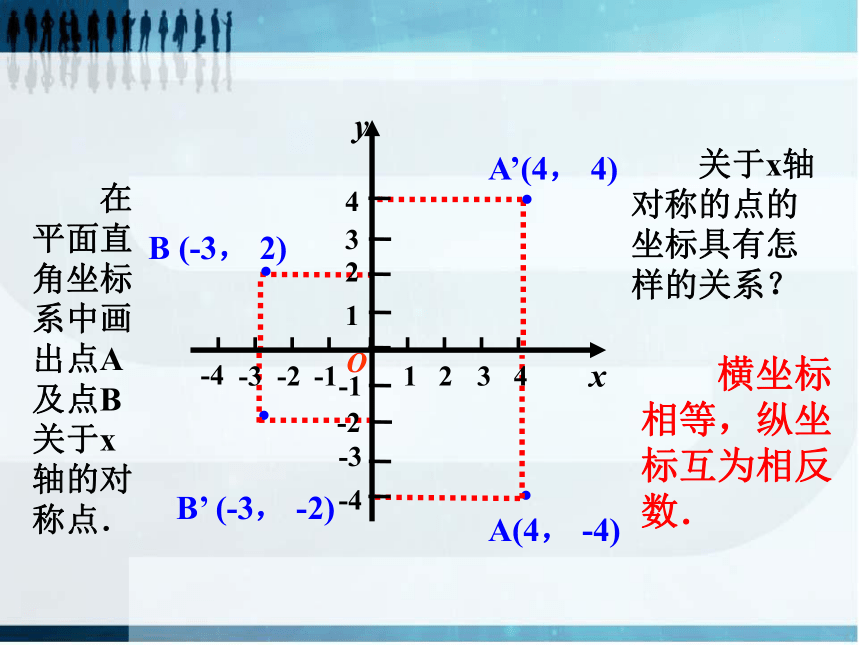
B (-3, 2)
·
·
A(4, -4)
·
B’ (-3, -2)
·
A’(4, 4)
在平面直角坐标系中画出点A及点B关于x轴的对称点.
关于x轴对称的点的坐标具有怎样的关系?
横坐标相等,纵坐标互为相反数.
3
1
4
2
-2
-4
-1
-3
O
1
2
3
4
-4
-3
-2
-1
x
y
·
A (3,3)
·
A’(-3,3)
在如图所示的平面直角坐标系中画出点A关于y轴的对称点.
3
1
4
2
-2
-4
-1
-3
O
1
2
3
4
-4
-3
-2
-1
x
y
点A与点A’的坐标有什么关系吗?
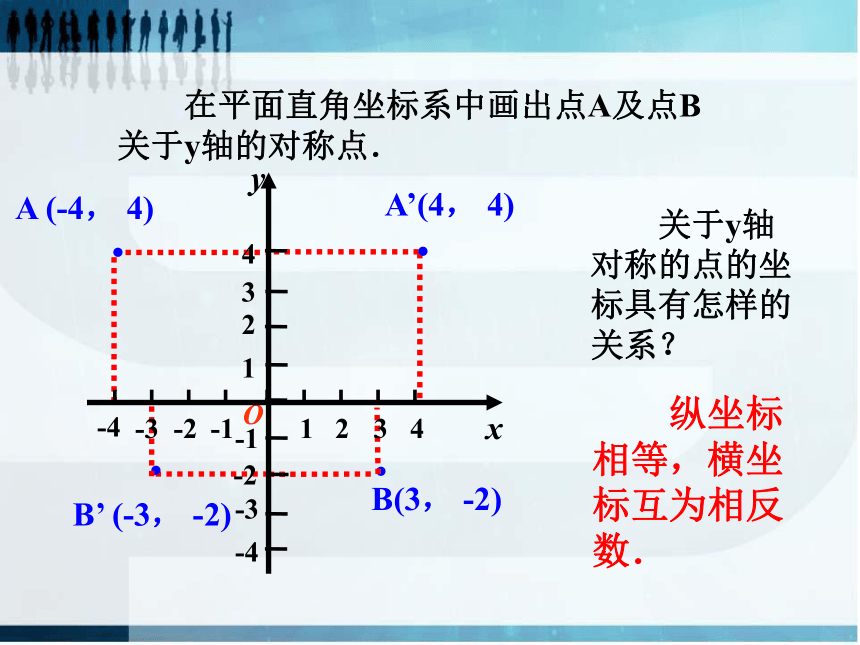
A (-4, 4)
·
·
B(3, -2)
·
B’ (-3, -2)
·
A’(4, 4)
在平面直角坐标系中画出点A及点B关于y轴的对称点.
关于y轴对称的点的坐标具有怎样的关系?
纵坐标相等,横坐标互为相反数.
3
1
4
2
-2
-4
-1
-3
O
1
2
3
4
-4
-3
-2
-1
x
y
在平面直角坐标系中,关于 x 轴对称的点的横坐标相等,纵坐标互为相反数.关于 y 轴对称的点的纵坐标相等,横坐标互为相反数.
即:
点(x,y)关于x轴对称的点的坐标为 ;
点(x,y)关于y轴对称的点的坐标为 .
(x,-y)
(-x,y)
结论
1.完成下表.
已知点 (7,-5) (-9,2) (-3,-1) (0,-8) (3,0)
关于x轴的对称点
关于y轴的对称点
(-7, -5)
(7,-5)
(-9,-2)
(9, 2)
(3, -1)
(-3, 1)
(0,-8)
(0,8)
(-3,0)
(3,0)
2.已知点A(2a,3b)与点A’(8,b+8).
若点A 与点A ’关于x轴对称,则a=____ b=_____.
若点A与点A’关于y轴对称,则a=____ b=_____.
4
-2
-4
4
练一练
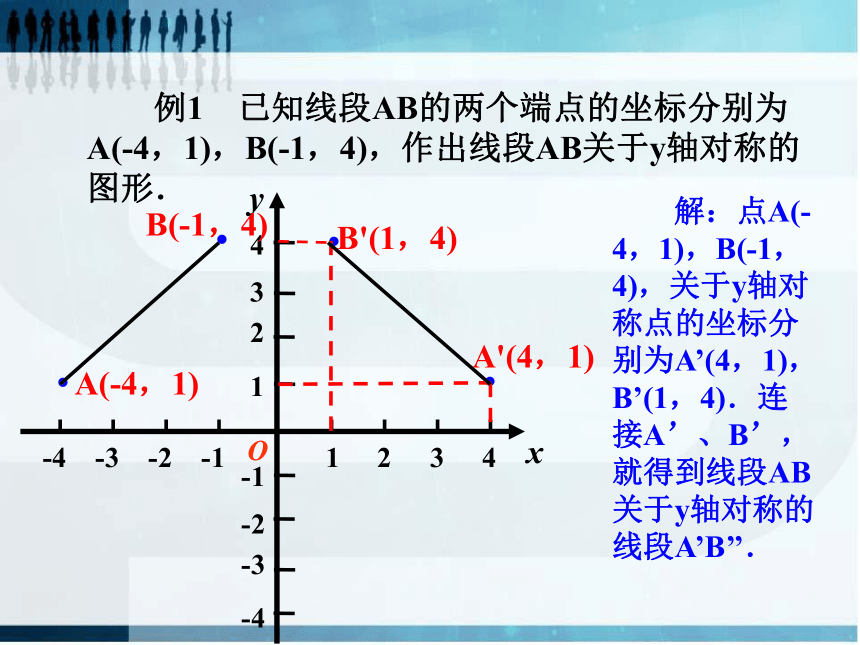
例1 已知线段AB的两个端点的坐标分别为A(-4,1),B(-1,4),作出线段AB关于y轴对称的图形.
3
1
4
2
-2
-4
-1
-3
O
1
2
3
4
-4
-3
-2
-1
x
y
·
·
A(-4,1)
B(-1,4)
·
·
A'(4,1)
B'(1,4)
解:点A(-4,1),B(-1,4),关于y轴对称点的坐标分别为A’(4,1),B’(1,4).连接A’、B’,就得到线段AB关于y轴对称的线段A’B’’.
例2 已知△ABC的三个顶点的坐标分别为A (-4,-1),B(- 1,2),C(-3,4),分别作出△ABC关于y轴和x轴对称的图形.
3
1
4
2
-2
-4
-1
-3
O
1
2
3
4
-4
-3
-2
-1
x
y
-3
-5
5
5
-5
·
·
·
A
C
B
·
·
·
·
·
·
C′
C″
A′
A″
B′
B″
解:点A(-4,-1),B(-1,2),C(-3,4),关于y轴对称点的坐标分别为A’(4,-1), B’(1,2),C’(3,4),依次连接A’、B’、C’三点,就得到△ABC关于y轴对称的△A’B’C’.
点A(-4,-1),B(-1,2),C(-3,4),关于x轴对称点的坐标分别为A″ (-4,1), B″ (-1,-2),C″ (-3,-4).依次连接A″、B″、C″三点,就得到△ABC关于y轴对称的△A″B″C″.
①先求出已知图形中的一些特殊点(如多边形的顶点)的对应点的坐标;
②描出这些对称点;
③依次连接各对称点就可以得到这个图形的轴对称图形.
结论
根据已知图形作关于x轴或y轴对称图形的步骤:
·
A
B
C
D
A′
B′
C′
D′
·
·
·
·
·
·
·
x
O
2 4
-4 -2
y
4
2
例3 四边形ABCD的四个顶点的坐标分别是A(-5,1),B(-2,1),C(-2,5),D(-5,4),分别作出与四边形ABCD关于y轴和x轴对称的图形.
解:点(x,y)关于y轴对称的点的坐标为(-x,y),因此四边形ABCD的顶点A、B、C、D关于y轴对称的点分别为A′(5,1)、B′(2,1)、C ′(2,5)、D ′ (5,4),依次连接A ′B ′,B ′C ′,C ′D ′,D ′A ′,就可得到四边形ABCD关于y 轴对称的四边形A ′B ′C ′D ′.
如图,分别作出点P,M,N关于直线x=1以及关于直线x=-1的对称点, 你能发现它们坐标之间分别有什么关系吗?
探究
·
C″(-1,-2)
·
x=1
·
·
·
·
·
A(-2,4)
C(-1, -2)
B’(5,-1)
B(-3,-1)
C’(3,-2)
A’(4,4)
3
1
4
2
5
-2
-4
-1
-3
1
2
3
4
5
-4
-3
-2
-1
y
x
O
x=-1
·
·
B″(1,-1)
A″(0,4)
点A(x, y)关于直线x=1对称的点的坐标为(-x+2,y);
点A (x, y)关于直线x= -1对称的点的坐标为(-x-2,y).
已知点 A(-2,4) B(-3,-1) C(-1,-2)
关于x=1对称点
关于x=-1对称点
B’(5,-1)
C’(3,-2)
A’(4,4)
B″(1,-1)
A″(0,4)
C″(-1,-2)
结论
1.在平面直角坐标系中,点 (x,y)关于
y轴对称点的坐标是________. 2.在平面直角坐标系中,点(x,y)关于
直线x=1对称点的坐标是________. 3.在平面直角坐标系中,点(x, y)关于
直线x=-1对称点的坐标是________. 4.在平面直角坐标系中,点 (x,y)关于
x轴对称点的坐标是________. 5.在平面直角坐标系中,点(x,y)关于
直线y=1对称点的坐标是________. 6.在平面直角坐标系中,点(x,y)关于
直线y=-1对称点的坐标是________.
(-x+2,y)
(-x-2,y)
(x,-y+2)
(x,-y-2)
在平面直角坐标系中,关于坐标轴和x=±1,y=±1 对称的点的坐标的特点:
(-x,y)
(x,-y)
①关于y轴对称点的坐标是(-x,y).
②关于直线x=1对称点的坐标是(-x+2,y).
③关于直线x=-1对称点的坐标是(-x-2,y).
④关于x轴对称点的坐标是(x,-y).
⑤关于直线y=1对称点的坐标是(x,-y+2) .
⑥关于直线y=-1对称点的坐标是(x,-y-2).
在平面直角坐标系中,点 (x,y)关于坐标轴和x=±1 ,y=±1 对称的点的坐标:
课堂小结
在平面直角坐标系中,根据已知图形的点的坐标作它的轴对称图形的步骤:
①先求出已知图形中的一些特殊点(如多边形的顶点)的对应点的坐标;
②描出这些对称点;
③依次连接各对称点就可以得到这个图形的轴对称图形.
已知点 (-2,9) (3,-4) (-2,5) (-1,-4) (0,-6) (6,0)
关于x轴的对称点
关于y轴的对称点
(-2,-9)
(2,9)
(3,4)
(-3,-4)
(-2,-5)
(2,5)
(-1,4)
(1,-4)
(0,6)
(0,-6)
(6,0)
(-6,0)
1.说出下列点关于x轴和y轴对称的点的坐标.
随堂练习
2.点M(a, 6)与点N(4, a+b)关于y轴对称,则
a=_____, b =_____.
-4
10
3.如图,已知△ABC三点的坐标,求作△ABC
关于x轴和y轴的对称图形.
3
1
4
2
-2
-4
-1
-3
O
1
2
3
4
-4
-3
-2
-1
x
y
-3
-5
5
5
-5
B(3,3)
·
·
·
A(-2,4)
C(4,-1)
2.
点 (3,6) (-7,9) (6,-1) (-3,-5) (0,10)
关于x轴对称 (3,-6) (-7,-9) (6,1) (-3,5) (0,-10)
关于y轴对称 (-3,6) (7,9) (-6,-1) (3,-5) (0,10)
习题答案
3.B(1,-1),C(-1,-1),D(-1,1).
6.(1)关于x轴对称;(2)向上平移5个单位长
度;
(3)关于y轴对称;(4)先关于x轴,再关于y轴
做轴对称.
7.小球运动轨迹是(3,0)→(0,3)→ (1,4)
→(5,0) → (8,3)→(7,4)→(3,0);
其中关于直线l对称的点有(1,4)与(7,4),
(0,3)与(8,3),(3,0)与(5,0).
8.点(x,y)关于直线m对称的点的坐标为(-
x+2,y),关于直线n对称的点的坐标为
(x,-y-2).
9.分别作出点A,B关于MN和l的对称点A′,
B′,连接A′B′,与MN和l分别相交于点
C,D,则路线ACDB即为所求.
一名游客在天安门广场向小明问西直门的位置,但他只知道东直门的位置,可是聪明的小明想了想,就准确的告诉了她,你知道原因吗?
东直门
(3.5,4)
西直门??
3
1
4
2
y
-2
-4
-1
-3
O
1
2
3
4
x
-4
-3
-2
-1
A
B
新课导入
知识与能力
教学目标
1.能在平面直角坐标系中画出点关于坐标轴对称的点;
2.掌握在平面直角坐标系中,关于x轴和y轴对称点的坐标特点,并能运用它解决简单的问题;
3.能在平面直角坐标系中画出一些简单的关于x轴和y轴的对称图形.
在找关于坐标轴对称的点的坐标之间规律并检验其正确性的过程中,培养语言表达能力、观察能力、归纳能力,养成良好的科学研究方法.
过程与方法
情感态度与价值观
在找点,绘图的过程中体验数形结合思想,体验学习的乐趣.
重点
难点
教学重难点
用坐标表示点关于坐标轴对称的点的坐标.
利用转化的思想,确定能代表轴对称图形的关键点.
·
A (3,3)
·
A’(3,-3)
点A与点A’的坐标有什么关系吗?
在如图所示的平面直角坐标系中画出点A关于x轴的对称点.
3
1
4
2
-2
-4
-1
-3
O
1
2
3
4
-4
-3
-2
-1
x
y
B (-3, 2)
·
·
A(4, -4)
·
B’ (-3, -2)
·
A’(4, 4)
在平面直角坐标系中画出点A及点B关于x轴的对称点.
关于x轴对称的点的坐标具有怎样的关系?
横坐标相等,纵坐标互为相反数.
3
1
4
2
-2
-4
-1
-3
O
1
2
3
4
-4
-3
-2
-1
x
y
·
A (3,3)
·
A’(-3,3)
在如图所示的平面直角坐标系中画出点A关于y轴的对称点.
3
1
4
2
-2
-4
-1
-3
O
1
2
3
4
-4
-3
-2
-1
x
y
点A与点A’的坐标有什么关系吗?
A (-4, 4)
·
·
B(3, -2)
·
B’ (-3, -2)
·
A’(4, 4)
在平面直角坐标系中画出点A及点B关于y轴的对称点.
关于y轴对称的点的坐标具有怎样的关系?
纵坐标相等,横坐标互为相反数.
3
1
4
2
-2
-4
-1
-3
O
1
2
3
4
-4
-3
-2
-1
x
y
在平面直角坐标系中,关于 x 轴对称的点的横坐标相等,纵坐标互为相反数.关于 y 轴对称的点的纵坐标相等,横坐标互为相反数.
即:
点(x,y)关于x轴对称的点的坐标为 ;
点(x,y)关于y轴对称的点的坐标为 .
(x,-y)
(-x,y)
结论
1.完成下表.
已知点 (7,-5) (-9,2) (-3,-1) (0,-8) (3,0)
关于x轴的对称点
关于y轴的对称点
(-7, -5)
(7,-5)
(-9,-2)
(9, 2)
(3, -1)
(-3, 1)
(0,-8)
(0,8)
(-3,0)
(3,0)
2.已知点A(2a,3b)与点A’(8,b+8).
若点A 与点A ’关于x轴对称,则a=____ b=_____.
若点A与点A’关于y轴对称,则a=____ b=_____.
4
-2
-4
4
练一练
例1 已知线段AB的两个端点的坐标分别为A(-4,1),B(-1,4),作出线段AB关于y轴对称的图形.
3
1
4
2
-2
-4
-1
-3
O
1
2
3
4
-4
-3
-2
-1
x
y
·
·
A(-4,1)
B(-1,4)
·
·
A'(4,1)
B'(1,4)
解:点A(-4,1),B(-1,4),关于y轴对称点的坐标分别为A’(4,1),B’(1,4).连接A’、B’,就得到线段AB关于y轴对称的线段A’B’’.
例2 已知△ABC的三个顶点的坐标分别为A (-4,-1),B(- 1,2),C(-3,4),分别作出△ABC关于y轴和x轴对称的图形.
3
1
4
2
-2
-4
-1
-3
O
1
2
3
4
-4
-3
-2
-1
x
y
-3
-5
5
5
-5
·
·
·
A
C
B
·
·
·
·
·
·
C′
C″
A′
A″
B′
B″
解:点A(-4,-1),B(-1,2),C(-3,4),关于y轴对称点的坐标分别为A’(4,-1), B’(1,2),C’(3,4),依次连接A’、B’、C’三点,就得到△ABC关于y轴对称的△A’B’C’.
点A(-4,-1),B(-1,2),C(-3,4),关于x轴对称点的坐标分别为A″ (-4,1), B″ (-1,-2),C″ (-3,-4).依次连接A″、B″、C″三点,就得到△ABC关于y轴对称的△A″B″C″.
①先求出已知图形中的一些特殊点(如多边形的顶点)的对应点的坐标;
②描出这些对称点;
③依次连接各对称点就可以得到这个图形的轴对称图形.
结论
根据已知图形作关于x轴或y轴对称图形的步骤:
·
A
B
C
D
A′
B′
C′
D′
·
·
·
·
·
·
·
x
O
2 4
-4 -2
y
4
2
例3 四边形ABCD的四个顶点的坐标分别是A(-5,1),B(-2,1),C(-2,5),D(-5,4),分别作出与四边形ABCD关于y轴和x轴对称的图形.
解:点(x,y)关于y轴对称的点的坐标为(-x,y),因此四边形ABCD的顶点A、B、C、D关于y轴对称的点分别为A′(5,1)、B′(2,1)、C ′(2,5)、D ′ (5,4),依次连接A ′B ′,B ′C ′,C ′D ′,D ′A ′,就可得到四边形ABCD关于y 轴对称的四边形A ′B ′C ′D ′.
如图,分别作出点P,M,N关于直线x=1以及关于直线x=-1的对称点, 你能发现它们坐标之间分别有什么关系吗?
探究
·
C″(-1,-2)
·
x=1
·
·
·
·
·
A(-2,4)
C(-1, -2)
B’(5,-1)
B(-3,-1)
C’(3,-2)
A’(4,4)
3
1
4
2
5
-2
-4
-1
-3
1
2
3
4
5
-4
-3
-2
-1
y
x
O
x=-1
·
·
B″(1,-1)
A″(0,4)
点A(x, y)关于直线x=1对称的点的坐标为(-x+2,y);
点A (x, y)关于直线x= -1对称的点的坐标为(-x-2,y).
已知点 A(-2,4) B(-3,-1) C(-1,-2)
关于x=1对称点
关于x=-1对称点
B’(5,-1)
C’(3,-2)
A’(4,4)
B″(1,-1)
A″(0,4)
C″(-1,-2)
结论
1.在平面直角坐标系中,点 (x,y)关于
y轴对称点的坐标是________. 2.在平面直角坐标系中,点(x,y)关于
直线x=1对称点的坐标是________. 3.在平面直角坐标系中,点(x, y)关于
直线x=-1对称点的坐标是________. 4.在平面直角坐标系中,点 (x,y)关于
x轴对称点的坐标是________. 5.在平面直角坐标系中,点(x,y)关于
直线y=1对称点的坐标是________. 6.在平面直角坐标系中,点(x,y)关于
直线y=-1对称点的坐标是________.
(-x+2,y)
(-x-2,y)
(x,-y+2)
(x,-y-2)
在平面直角坐标系中,关于坐标轴和x=±1,y=±1 对称的点的坐标的特点:
(-x,y)
(x,-y)
①关于y轴对称点的坐标是(-x,y).
②关于直线x=1对称点的坐标是(-x+2,y).
③关于直线x=-1对称点的坐标是(-x-2,y).
④关于x轴对称点的坐标是(x,-y).
⑤关于直线y=1对称点的坐标是(x,-y+2) .
⑥关于直线y=-1对称点的坐标是(x,-y-2).
在平面直角坐标系中,点 (x,y)关于坐标轴和x=±1 ,y=±1 对称的点的坐标:
课堂小结
在平面直角坐标系中,根据已知图形的点的坐标作它的轴对称图形的步骤:
①先求出已知图形中的一些特殊点(如多边形的顶点)的对应点的坐标;
②描出这些对称点;
③依次连接各对称点就可以得到这个图形的轴对称图形.
已知点 (-2,9) (3,-4) (-2,5) (-1,-4) (0,-6) (6,0)
关于x轴的对称点
关于y轴的对称点
(-2,-9)
(2,9)
(3,4)
(-3,-4)
(-2,-5)
(2,5)
(-1,4)
(1,-4)
(0,6)
(0,-6)
(6,0)
(-6,0)
1.说出下列点关于x轴和y轴对称的点的坐标.
随堂练习
2.点M(a, 6)与点N(4, a+b)关于y轴对称,则
a=_____, b =_____.
-4
10
3.如图,已知△ABC三点的坐标,求作△ABC
关于x轴和y轴的对称图形.
3
1
4
2
-2
-4
-1
-3
O
1
2
3
4
-4
-3
-2
-1
x
y
-3
-5
5
5
-5
B(3,3)
·
·
·
A(-2,4)
C(4,-1)
2.
点 (3,6) (-7,9) (6,-1) (-3,-5) (0,10)
关于x轴对称 (3,-6) (-7,-9) (6,1) (-3,5) (0,-10)
关于y轴对称 (-3,6) (7,9) (-6,-1) (3,-5) (0,10)
习题答案
3.B(1,-1),C(-1,-1),D(-1,1).
6.(1)关于x轴对称;(2)向上平移5个单位长
度;
(3)关于y轴对称;(4)先关于x轴,再关于y轴
做轴对称.
7.小球运动轨迹是(3,0)→(0,3)→ (1,4)
→(5,0) → (8,3)→(7,4)→(3,0);
其中关于直线l对称的点有(1,4)与(7,4),
(0,3)与(8,3),(3,0)与(5,0).
8.点(x,y)关于直线m对称的点的坐标为(-
x+2,y),关于直线n对称的点的坐标为
(x,-y-2).
9.分别作出点A,B关于MN和l的对称点A′,
B′,连接A′B′,与MN和l分别相交于点
C,D,则路线ACDB即为所求.
