11.4算法案例_课件1(1)-湘教版数学必修5(31张PPT)
文档属性
| 名称 | 11.4算法案例_课件1(1)-湘教版数学必修5(31张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 602.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-01 00:00:00 | ||
图片预览











文档简介
【课标要求】
1.理解辗转相除法与二分法及中国剩余定理的含义,了解其执行过程.
2.掌握秦九韶算法的计算过程,并了解它提高计算效率的实质.
算法案例
自学导引
1.辗转相除法是用于求 的一种方法.
所谓辗转相除法,就是对于给定的两个正整数,用较大的数除以较小的数.若余数 ,则将余数和较小的数构成新的一对数,继续上面的除法,直到大数被小数 ,则这时的小数就是原来两个数的最大公约数.
两个数的最大公约数
不为零
除尽
x0
x0
(a,x0)
4.秦九韶算法是我国南宋数学家 在他的代表作 中提出的一种用于计算 的方法.
对于任意一元n次多项式,秦九韶算法的步骤是:
首先将多项式改写为
P(x)=anxn+an-1xn-1+…+a1x+a0
=(anxn-1+an-1xn-2+…+a1)x+a0
=((anxn-2+an-1xn-3+…+a2)x+a1)x+a0
=(…((anx+an-1)x+an-2)x+…+a1)x+a0.
令vk=(…(anx+an-1)x+…+an-(k-1))x+an-k,
秦九韶
《数学九章》
一元n次多项式的值
an
vk-1x+ a n-k
说明:①计算时,首先计算最内层的括号,然后由内向外逐层计算,直到最外层的一个括号,然后加上常数项.
②利用上面方法求一元n次多项式值的计算量仅需n次乘法和n次加法.
自主探究
1.任意给定两个正整数,用辗转相除法和更相减损术是否都可以求它们的最大公约数?
答案 是.更相减损术与辗转相除法都能在有限步内结束,故均可以用来求两个正整数的最大公约数.
2.秦九韶算法与直接计算相比有什么优缺点?
(2)秦九韶算法:利用秦九韶算法求上述f(5)时只需要进行4次乘法运算和5次加减运算即可.与直接计算相比大大节省了乘法运算的次数,还避免了对自变量x单独做幂的计算,而与系数一起逐步增长幂次,从而提高计算的精度.又如利用秦九韶算法求多项式f(x)=anxn+an-1xn-1+…+a1x+a0的值时,通过转化把乘法运算的次数减少到最多n次,加减运算最多n次.
预习测评
1.用辗转相除法求36与134的最大公约数,第一步是( ).
A.134-36=98
B.134=3×36+26
C.先除以2,得到18与67
D.134÷36=3(余26)
答案 B
2.求数320和2 400的最大公约数为________.
答案 160
答案 an-k 循环
要点阐释
1.辗转相除法
(1)所谓辗转相除法,就是对于给定的两个数,用较大的数除以较小的数.若余数不为零,则将余数和较小的数构成新的一对数,继续上面的除法,直到大数被小数除尽,则这时的较小的数就是原来两个数的最大公约数.
(2)算法步骤:(以求两正整数a,b的最大公约数为例)
S1:输入两个正整数a,b(a>b);
S2:把a÷b的余数赋予r;
S3:如果r≠0,那么把b赋予a,把r赋予b,转到第二步,否则转到第四步;
S4:输出最大公约数b.
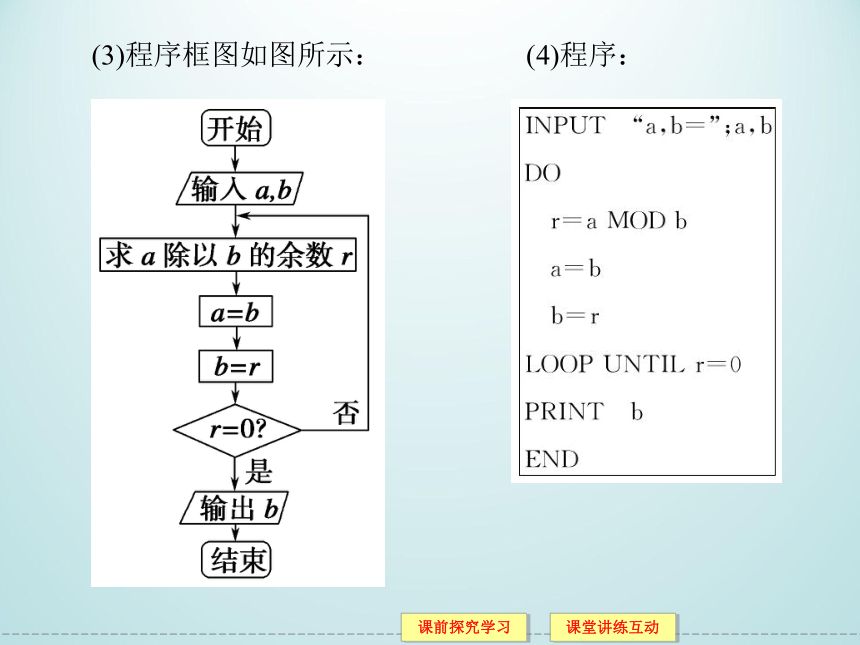
(3)程序框图如图所示: (4)程序:
程序框图如图 伪代码:
程序框图,如图 伪代码:
4.秦九韶算法
(1)特点:通过一次式的反复计算,逐步得出高次多项式的值,对于一个n次多项式,只需做n次乘法和n次加法即可.
(2)算法步骤:
设Pn(x)=anxn+an-1xn-1+…+a1x+a0,将其改写为
Pn(x)=(anxn-1+an-1xn-2+…+a1)x+a0
=((anxn-2+an-1xn-3+…+a2)x+a1)x+a0
=(…((anx+an-1)x+an-2)x+…+a1)x+a0.
S1:计算最内层anx+an-1的值,将anx+an-1的值赋给一个变量v1(为方便将an赋予变量v0);
S2:计算(anx+an-1)x+an-2的值,可以改写为v1x+an-2,将v1x+an-2的值赋给一个变量v2;
依次类推,即每一步的计算之后都赋予一个新值vk,即从最内层的括号到最外层括号的值依次赋予变量v1,v2,…,vk,…,vn,第n步所求值vn=vn-1x+a0即为所求多项式的值.
典例剖析
题型一 最大公约数的求法
【例1】 用辗转相除法求下列两组数的最大公约数,并用更相减损术检验你的结果.
(1)80,36;(2)294,84.
解 (1)80=36×2+8,
36=8×4+4,8=4×2+0,
即80与36的最大公约数是4.
验证:
80÷2=40 36÷2=18
40÷2=20 18÷2=9
20—9=11 11-9=2
9-2=7 7-2=5
5-2=3 3-2=1
2-1=1 1×2×2=4
所以80与36的最大公约数为4.
(2)294=84×3+42,84=42×2,
即294与84的最大公约数是42.
验证:因为294与84都是偶数,可同时除以2,
即取147与42的最大公约数后再乘2.
147-42=105 105-42=63
63-42=21 42-21=21
所以294与84的最大公约数为21×2=42.
方法点评 使用辗转相除法,我们可依据a=nb+r这个式子,反复执行,直到r=0为止,用更相减损术就是根据r=a-b这个式子,反复执行,直到r=b为止.
1.求261,319的最大公约数.
解 法一 (辗转相除法)
319=261×1+58,
261=58×4+29,
58=29×2,
∴319与261的最大公约数是29.
法二 (更相减损术)
319-261=58
261-58=203
203-58=145
145-58=87
87-58=29
58-29=29
∴319与261的最大公约数是29.
题型二 中国剩余定理及二分法
【例2】 写出下列程序框图的用途,并将其伪代码写出.
2.写出用二分法求方程x2-2=0的近似解的一个算法,并假设所求近似解与精确解的差的绝对值不超过0.005.
题型三 秦九韶算法的应用
【例3】 用秦九韶算法求多项式f(x)=1+x+0.5x2+0.16 667x3+0.04 167x4+0.00 833x5,当x=-0.2时的值.
解 根据秦九韶算法,把多项式改写成如下形式:
f(x)=((((0.00 833x+0.04 167)x+0.16 667)x+0.5)x+1)x+1.
按照从内到外的顺序依次计算一次多项式当x=-0.2时的值:
v0=0.00 833;
v1=0.00 833×(-0.2)+0.04 167=0.04:
v2=0.04×(-0.2)+0.16 667=0.15 867:
v3=0.15 867×(-0.2)+0.5=0.46 827:
v4=0.46 827×(-0.2)+1=0.90 635:
v5=0.90 635×(-0.2)+1=0.81 873.
所以当x=-0.2时,多项式的值为0.81 873.
方法点评 秦九韶算法减少了运算的次数,因此它是多项式求值的简捷方法.此类题目的易错点有二,一是初始值的确定,即v0=an,易错写成v0=a0;二是vk的计算,即vk=vk-1x+an-k(k=1,2,…,n),易错写成vk=vk-1x+ak.
3.用秦九韶算法求多项式f(x)=8x7+5x6+3x4+2x+1当x=2时的值.
解 根据秦九韶算法,把多项式改写成如下形式:
f(x)=8x7+5x6+0·x5+3x4+0·x3+0·x2+2x+1=((((((8x+5)x+0)x+3)x+0)x+0)x+2)x+1.
按照从内到外的顺序,依次计算一次多项式当x=2时的值.
v0=8;
v1=8×2+5=21;
v2=21×2+0=42;
v3=42×2+3=87;
v4=87×2+0=174;
v5=174×2+0=348;
v6=348×2+2=698:
v7=698×2+1=1 397.
所以当x=2时,多项式的值为1 397.
误区警示 由于对秦九韶算法的步骤使用不当而致误
【例4】 f(x)=3x4+2x2+4x+2,求f(-2)的值.
[错解] f(x)=((3x2+2)x+4)x+2,
v1=3×(-2)2+2=14,
v2=14×(-2)+4=-24,
v3=-24×(-2)+2=50,
∴f(-2)=50.
错因分析 错解中v1中含有x的二次式,不符合“秦九韶算法”.
[正解] f(x)=3x4+0·x3+2x2+4x+2
=(((3x+0)x+2)x+4)x+2,
v0=3,
v1=3×(-2)+0=-6,
v2=-6×(-2)+2=14,
v3=14×(-2)+4=-24,
v4=-24×(-2)+2=50,
∴f(-2)=50.
纠错心得 当一元多项式函数中出现空项时要把系数为零的相应项补齐,否则,在处理问题时,多项式的运算的次数不会达到对应的次数,从而得出错误的结果.
1.理解辗转相除法与二分法及中国剩余定理的含义,了解其执行过程.
2.掌握秦九韶算法的计算过程,并了解它提高计算效率的实质.
算法案例
自学导引
1.辗转相除法是用于求 的一种方法.
所谓辗转相除法,就是对于给定的两个正整数,用较大的数除以较小的数.若余数 ,则将余数和较小的数构成新的一对数,继续上面的除法,直到大数被小数 ,则这时的小数就是原来两个数的最大公约数.
两个数的最大公约数
不为零
除尽
x0
x0
(a,x0)
4.秦九韶算法是我国南宋数学家 在他的代表作 中提出的一种用于计算 的方法.
对于任意一元n次多项式,秦九韶算法的步骤是:
首先将多项式改写为
P(x)=anxn+an-1xn-1+…+a1x+a0
=(anxn-1+an-1xn-2+…+a1)x+a0
=((anxn-2+an-1xn-3+…+a2)x+a1)x+a0
=(…((anx+an-1)x+an-2)x+…+a1)x+a0.
令vk=(…(anx+an-1)x+…+an-(k-1))x+an-k,
秦九韶
《数学九章》
一元n次多项式的值
an
vk-1x+ a n-k
说明:①计算时,首先计算最内层的括号,然后由内向外逐层计算,直到最外层的一个括号,然后加上常数项.
②利用上面方法求一元n次多项式值的计算量仅需n次乘法和n次加法.
自主探究
1.任意给定两个正整数,用辗转相除法和更相减损术是否都可以求它们的最大公约数?
答案 是.更相减损术与辗转相除法都能在有限步内结束,故均可以用来求两个正整数的最大公约数.
2.秦九韶算法与直接计算相比有什么优缺点?
(2)秦九韶算法:利用秦九韶算法求上述f(5)时只需要进行4次乘法运算和5次加减运算即可.与直接计算相比大大节省了乘法运算的次数,还避免了对自变量x单独做幂的计算,而与系数一起逐步增长幂次,从而提高计算的精度.又如利用秦九韶算法求多项式f(x)=anxn+an-1xn-1+…+a1x+a0的值时,通过转化把乘法运算的次数减少到最多n次,加减运算最多n次.
预习测评
1.用辗转相除法求36与134的最大公约数,第一步是( ).
A.134-36=98
B.134=3×36+26
C.先除以2,得到18与67
D.134÷36=3(余26)
答案 B
2.求数320和2 400的最大公约数为________.
答案 160
答案 an-k 循环
要点阐释
1.辗转相除法
(1)所谓辗转相除法,就是对于给定的两个数,用较大的数除以较小的数.若余数不为零,则将余数和较小的数构成新的一对数,继续上面的除法,直到大数被小数除尽,则这时的较小的数就是原来两个数的最大公约数.
(2)算法步骤:(以求两正整数a,b的最大公约数为例)
S1:输入两个正整数a,b(a>b);
S2:把a÷b的余数赋予r;
S3:如果r≠0,那么把b赋予a,把r赋予b,转到第二步,否则转到第四步;
S4:输出最大公约数b.
(3)程序框图如图所示: (4)程序:
程序框图如图 伪代码:
程序框图,如图 伪代码:
4.秦九韶算法
(1)特点:通过一次式的反复计算,逐步得出高次多项式的值,对于一个n次多项式,只需做n次乘法和n次加法即可.
(2)算法步骤:
设Pn(x)=anxn+an-1xn-1+…+a1x+a0,将其改写为
Pn(x)=(anxn-1+an-1xn-2+…+a1)x+a0
=((anxn-2+an-1xn-3+…+a2)x+a1)x+a0
=(…((anx+an-1)x+an-2)x+…+a1)x+a0.
S1:计算最内层anx+an-1的值,将anx+an-1的值赋给一个变量v1(为方便将an赋予变量v0);
S2:计算(anx+an-1)x+an-2的值,可以改写为v1x+an-2,将v1x+an-2的值赋给一个变量v2;
依次类推,即每一步的计算之后都赋予一个新值vk,即从最内层的括号到最外层括号的值依次赋予变量v1,v2,…,vk,…,vn,第n步所求值vn=vn-1x+a0即为所求多项式的值.
典例剖析
题型一 最大公约数的求法
【例1】 用辗转相除法求下列两组数的最大公约数,并用更相减损术检验你的结果.
(1)80,36;(2)294,84.
解 (1)80=36×2+8,
36=8×4+4,8=4×2+0,
即80与36的最大公约数是4.
验证:
80÷2=40 36÷2=18
40÷2=20 18÷2=9
20—9=11 11-9=2
9-2=7 7-2=5
5-2=3 3-2=1
2-1=1 1×2×2=4
所以80与36的最大公约数为4.
(2)294=84×3+42,84=42×2,
即294与84的最大公约数是42.
验证:因为294与84都是偶数,可同时除以2,
即取147与42的最大公约数后再乘2.
147-42=105 105-42=63
63-42=21 42-21=21
所以294与84的最大公约数为21×2=42.
方法点评 使用辗转相除法,我们可依据a=nb+r这个式子,反复执行,直到r=0为止,用更相减损术就是根据r=a-b这个式子,反复执行,直到r=b为止.
1.求261,319的最大公约数.
解 法一 (辗转相除法)
319=261×1+58,
261=58×4+29,
58=29×2,
∴319与261的最大公约数是29.
法二 (更相减损术)
319-261=58
261-58=203
203-58=145
145-58=87
87-58=29
58-29=29
∴319与261的最大公约数是29.
题型二 中国剩余定理及二分法
【例2】 写出下列程序框图的用途,并将其伪代码写出.
2.写出用二分法求方程x2-2=0的近似解的一个算法,并假设所求近似解与精确解的差的绝对值不超过0.005.
题型三 秦九韶算法的应用
【例3】 用秦九韶算法求多项式f(x)=1+x+0.5x2+0.16 667x3+0.04 167x4+0.00 833x5,当x=-0.2时的值.
解 根据秦九韶算法,把多项式改写成如下形式:
f(x)=((((0.00 833x+0.04 167)x+0.16 667)x+0.5)x+1)x+1.
按照从内到外的顺序依次计算一次多项式当x=-0.2时的值:
v0=0.00 833;
v1=0.00 833×(-0.2)+0.04 167=0.04:
v2=0.04×(-0.2)+0.16 667=0.15 867:
v3=0.15 867×(-0.2)+0.5=0.46 827:
v4=0.46 827×(-0.2)+1=0.90 635:
v5=0.90 635×(-0.2)+1=0.81 873.
所以当x=-0.2时,多项式的值为0.81 873.
方法点评 秦九韶算法减少了运算的次数,因此它是多项式求值的简捷方法.此类题目的易错点有二,一是初始值的确定,即v0=an,易错写成v0=a0;二是vk的计算,即vk=vk-1x+an-k(k=1,2,…,n),易错写成vk=vk-1x+ak.
3.用秦九韶算法求多项式f(x)=8x7+5x6+3x4+2x+1当x=2时的值.
解 根据秦九韶算法,把多项式改写成如下形式:
f(x)=8x7+5x6+0·x5+3x4+0·x3+0·x2+2x+1=((((((8x+5)x+0)x+3)x+0)x+0)x+2)x+1.
按照从内到外的顺序,依次计算一次多项式当x=2时的值.
v0=8;
v1=8×2+5=21;
v2=21×2+0=42;
v3=42×2+3=87;
v4=87×2+0=174;
v5=174×2+0=348;
v6=348×2+2=698:
v7=698×2+1=1 397.
所以当x=2时,多项式的值为1 397.
误区警示 由于对秦九韶算法的步骤使用不当而致误
【例4】 f(x)=3x4+2x2+4x+2,求f(-2)的值.
[错解] f(x)=((3x2+2)x+4)x+2,
v1=3×(-2)2+2=14,
v2=14×(-2)+4=-24,
v3=-24×(-2)+2=50,
∴f(-2)=50.
错因分析 错解中v1中含有x的二次式,不符合“秦九韶算法”.
[正解] f(x)=3x4+0·x3+2x2+4x+2
=(((3x+0)x+2)x+4)x+2,
v0=3,
v1=3×(-2)+0=-6,
v2=-6×(-2)+2=14,
v3=14×(-2)+4=-24,
v4=-24×(-2)+2=50,
∴f(-2)=50.
纠错心得 当一元多项式函数中出现空项时要把系数为零的相应项补齐,否则,在处理问题时,多项式的运算的次数不会达到对应的次数,从而得出错误的结果.
同课章节目录
