12.4.2回归直线_课件1-湘教版数学必修5(39张PPT)
文档属性
| 名称 | 12.4.2回归直线_课件1-湘教版数学必修5(39张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-01 00:00:00 | ||
图片预览










文档简介
数据的相关性
相关性
回归直线
回
归
直
线
课堂互动讲练
课前自主学案
学习目标
1.理解两个变量的相关关系的概念;
2.会作散点图,并利用散点图判断两个变量之间是否具有相关关系;
3.会求回归直线方程.
课前自主学案
1.用样本估计总体主要有:用样本的_____________估计总体的频率分布;用样本的_____________估计总体的数字特征.
2.样本的数字特征主要有_________、________、__________、________及____________。
3.在现实生活中两个变量之间的函数关系是一种_______的关系.
温故夯基
频率分布
数字特征
平均数
众数
中位数
方差
标准差
确定
1.相关关系
与函数关系不同,相关关系是一种_________性关系.
2.两个变量的线性相关
(1)散点图:将样本中n个数据点(xi,yi)(i=1,2,…,n)描在平面直角坐标系中得到的图形.
(2)正相关与负相关
①正相关:散点图中的点散布在从________到___________的区域.
非确定
左下角
右上角
知新益能
②负相关:散点图中的点散布在从__________到__________的区域.
3.回归直线的方程
(1)回归直线:如果散点图中点的分布从整体上看大致在____________附近,就称这两个变量之间具有______________关系,这条直线叫做回归直线.
(2)回归方程:_____________对应的方程叫回归直线的方程,简称回归方程.
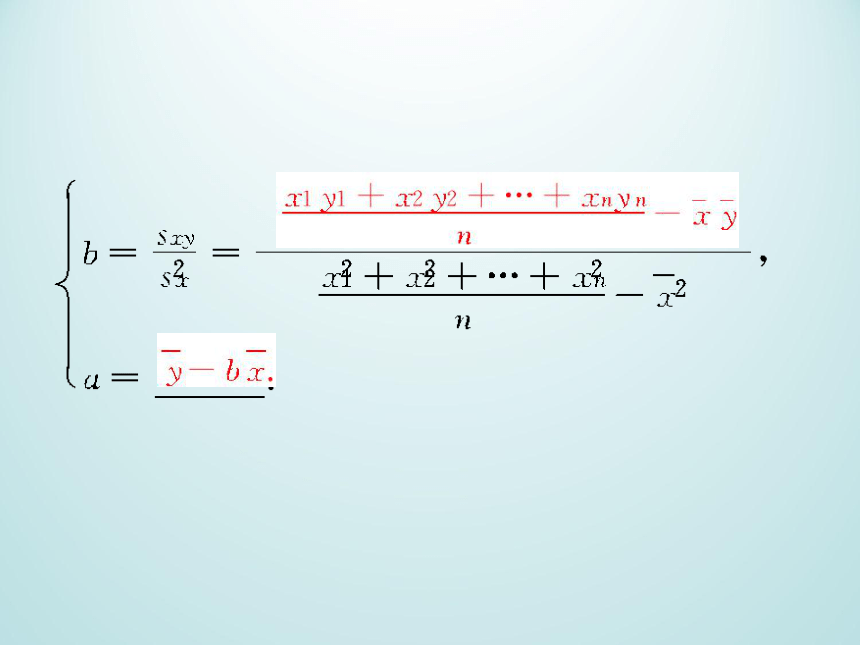
(3)回归直线方程y=bx+a,其中
左上角
右下角
一条直线
线性相关
回归直线
b是回归方程的斜率,a是截距.
4.最小二乘估计
我们可以求Q(a,b)=_________________的最小值,如果常数a,b使Q(a,b)达到最小,就称直线l:y=bx+a为{xi}与{yi}的回归直线,回归直线中的a、b分别是固有值a0、b0的最小二乘估计.
1.相关关系与函数关系有什么不同?
提示:函数关系是一种确定的关系,相关关系是一种非确定的关系.函数关系是一种因果关系,而相关关系不一定是因果关系,也可能是伴随关系.
2.回归直线通过样本点的中心,对照平均数与样本数据之间的关系,你能说说回归直线与散点图中各点之间的关系吗?
问题探究
3.“回归直线”方程能否按解析几何中求直线方程的方法来求?
提示:不能.求回归直线方程的方法是用最小二乘估计.因为所有数据点都分布在一条直线附近时,这样的直线可画出许多条,而“回归直线”是这些直线中“最贴近”已知数据的,但并不一定过数据中的某个点,故一般不按解析几何中求直线方程的方法来求.
课堂互动讲练
相关关系的判断
考点突破
在现实生活中存在着大量的相关关系,如何判断和描述相关关系,统计学发挥着非常重要的作用.由于变量间的相关关系带有不确定性,这就需要通过收集大量的数据,对数据进行统计分析,发现规律,从而作出科学的判断.
以下是在某地搜集到的不同楼盘新房屋的销售价格y(单位:万元)和房屋面积x(单位:m2)的数据:
例1
房屋面积x(m2)
115
110
80
135
105
销售价格y(万元)
24.8
21.6
19.4
29.2
22
(1)画出数据对应的散点图;
(2)判断新房屋的销售价格和房屋面积之间是否具有相关关系?如果有相关关系,是正相关还是负相关?
【思路点拨】 先建立直角坐标系,画出散点图,再判断相关关系.
【解】 (1)数据对应的散点图如图所示.
(2)通过以上数据对应的散点图可以判断,新房屋的销售价格和房屋的面积之间具有相关关系,且是正相关.
【名师点评】 两个随机变量x和y相关关系的确定方法:
(1)散点图法:通过散点图,观察它们的分布是否存在一定规律,直观地判断;
(2)表格、关系式法:结合表格或关系式进行判断;
(3)经验法:借助积累的经验进行分析判断.
变式训练1 某地农业技术指导站的技术员,经过在7块并排大小相同的试验田上进行施化肥量对水稻产量影响的试验,得到如下表所示的一组数据:(单位:千克)
施化肥量x
15
20
25
30
35
40
45
水稻产量y
330
345
365
405
445
450
455
施化肥量x和水稻产量y是否具有相关关系?
解:作出散点图进行分析.散点图如下:
从散点图可以看出施化肥量x和水稻产量y的确存在一定相关关系,大体上随着施化肥量的增加,水稻的产量也在增加.
求回归直线方程
据最小二乘估计思想的公式,用待定系数法求出a,b,从而确定回归直线方程.
5个学生的数学和物理成绩(单位:分)如下表:
例2
学生
学科
A
B
C
D
E
数学
80
75
70
65
60
物理
70
66
68
64
62
画出散点图,判断它们是否具有相关关系,若相关,求出回归方程.
【解】 以x轴表示数学成绩,y轴表示物理成绩,可得到相应的散点图如图所示.
由散点图可知,两者之间具有相关关系,且为线性相关.
列表,计算
i
1
2
3
4
5
xi
80
75
70
65
60
yi
70
66
68
64
62
x i y i
5600
4950
4760
4160
3720
6400
5625
4900
4225
3600
变式训练2 随着我国经济的快速发展,城乡居民的生活水平不断提高,为研究某市家庭平均收入与月平均生活支出的关系,该市统计部门随机调查10个家庭,得数据如下表:
家庭编号
1
2
3
4
5
6
7
8
9
10
xi(收入)/千元
0.8
1.1
1.3
1.5
1.5
1.8
2.0
2.2
2.4
2.8
yi(支出)/千元
0.7
1.0
1.2
1.0
1.3
1.5
1.3
1.7
2.0
2.5
(1)判断家庭平均收入与月平均生活支出是否相关;
(2)若二者线性相关,求回归直线方程.
解:(1)作出散点图:
观察发现各个数据对应的点都在一条直线附近,所以二者有线性相关关系
利用回归直线,我们可以进行预测.若回归直线方程为y=bx+a,则x=x0处的估计值为:y=bx0+a.
某5名学生总成绩和数学成绩(单位:分)如下表所示:
利用回归方程对总体进行估计
例3
学生
A
B
C
D
E
总成绩(x)
482
383
421
364
362
数学成绩(y)
78
65
71
64
61
(1)作出散点图;
(2)求数学成绩y对总成绩x的回归方程;
(3)如果一个学生的总成绩为450分,试预测这个学生的数学成绩.
【思路点拨】 进行线性回归分析的关键是求出线性回归直线方程.由于求回归系数a、b的运算量很大,故可用列表法并借助计算器求解.
【解】 (1)散点图如图所示:
(2)列表:
i
1
2
3
4
5
xi
482
383
421
364
362
yi
78
65
71
64
61
x i y i
37596
24895
29891
23296
22082
【名师点评】 (1)回归分析是寻找相关关系中非确定性关系的某种确定性;
(2)求回归直线方程,关键在于正确地求出系数a,b,由于a,b的计算量大,计算时要仔细,避免计算失误.
变式训练3 一台机器由于使用时间较长,生产的零件有一些会缺损,按不同转速生产出来的零件有缺损的统计数据如下表:
转速x(转/秒)
16
14
12
8
每小时生产缺损零件数y(件)
11
9
8
5
(1)作出散点图;
(2)如果y与x线性相关,求出回归直线方程;
(3)若实际生产中,允许每小时的产品中有缺损的零件最多为10个,那么,机器的运转速度应控制在什么范围?
解:(1)根据表中的数据画出散点图如图:
(2)设回归直线方程为:y=bx+a,并列表如下:
i
1
2
3
4
xi
16
14
12
8
yi
11
9
8
5
xiyi
176
126
96
40
1.在研究两个变量是否存在某种关系时,必须从散点图入手,对于散点图,可以做出如下判断:(1)如果所有的样本点都落在某一函数曲线上,那么就用该函数来描述变量之间的关系,即变量之间具有函数关系;(2)如果所有的样本点都落在某一函数曲线附近,那么变量之间具有相关关系;(3)如果所有的样本点都落在某一直线附近,那么变量之间具有线性相关关系.
方法感悟
2.知道x与y呈线性相关关系,无需进行相关性检验,否则,应首先进行相关性检验,如果本身两个变量不具备相关关系,或者说,它们之间相关关系不显著,即使求出回归直线方程也是毫无意义的,而且用其估计和预测的量也是不可信的.
3.利用回归方程估计总体,只是反映了x与y的一种近似的相关关系,即y值并不一定是真实值.
相关性
回归直线
回
归
直
线
课堂互动讲练
课前自主学案
学习目标
1.理解两个变量的相关关系的概念;
2.会作散点图,并利用散点图判断两个变量之间是否具有相关关系;
3.会求回归直线方程.
课前自主学案
1.用样本估计总体主要有:用样本的_____________估计总体的频率分布;用样本的_____________估计总体的数字特征.
2.样本的数字特征主要有_________、________、__________、________及____________。
3.在现实生活中两个变量之间的函数关系是一种_______的关系.
温故夯基
频率分布
数字特征
平均数
众数
中位数
方差
标准差
确定
1.相关关系
与函数关系不同,相关关系是一种_________性关系.
2.两个变量的线性相关
(1)散点图:将样本中n个数据点(xi,yi)(i=1,2,…,n)描在平面直角坐标系中得到的图形.
(2)正相关与负相关
①正相关:散点图中的点散布在从________到___________的区域.
非确定
左下角
右上角
知新益能
②负相关:散点图中的点散布在从__________到__________的区域.
3.回归直线的方程
(1)回归直线:如果散点图中点的分布从整体上看大致在____________附近,就称这两个变量之间具有______________关系,这条直线叫做回归直线.
(2)回归方程:_____________对应的方程叫回归直线的方程,简称回归方程.
(3)回归直线方程y=bx+a,其中
左上角
右下角
一条直线
线性相关
回归直线
b是回归方程的斜率,a是截距.
4.最小二乘估计
我们可以求Q(a,b)=_________________的最小值,如果常数a,b使Q(a,b)达到最小,就称直线l:y=bx+a为{xi}与{yi}的回归直线,回归直线中的a、b分别是固有值a0、b0的最小二乘估计.
1.相关关系与函数关系有什么不同?
提示:函数关系是一种确定的关系,相关关系是一种非确定的关系.函数关系是一种因果关系,而相关关系不一定是因果关系,也可能是伴随关系.
2.回归直线通过样本点的中心,对照平均数与样本数据之间的关系,你能说说回归直线与散点图中各点之间的关系吗?
问题探究
3.“回归直线”方程能否按解析几何中求直线方程的方法来求?
提示:不能.求回归直线方程的方法是用最小二乘估计.因为所有数据点都分布在一条直线附近时,这样的直线可画出许多条,而“回归直线”是这些直线中“最贴近”已知数据的,但并不一定过数据中的某个点,故一般不按解析几何中求直线方程的方法来求.
课堂互动讲练
相关关系的判断
考点突破
在现实生活中存在着大量的相关关系,如何判断和描述相关关系,统计学发挥着非常重要的作用.由于变量间的相关关系带有不确定性,这就需要通过收集大量的数据,对数据进行统计分析,发现规律,从而作出科学的判断.
以下是在某地搜集到的不同楼盘新房屋的销售价格y(单位:万元)和房屋面积x(单位:m2)的数据:
例1
房屋面积x(m2)
115
110
80
135
105
销售价格y(万元)
24.8
21.6
19.4
29.2
22
(1)画出数据对应的散点图;
(2)判断新房屋的销售价格和房屋面积之间是否具有相关关系?如果有相关关系,是正相关还是负相关?
【思路点拨】 先建立直角坐标系,画出散点图,再判断相关关系.
【解】 (1)数据对应的散点图如图所示.
(2)通过以上数据对应的散点图可以判断,新房屋的销售价格和房屋的面积之间具有相关关系,且是正相关.
【名师点评】 两个随机变量x和y相关关系的确定方法:
(1)散点图法:通过散点图,观察它们的分布是否存在一定规律,直观地判断;
(2)表格、关系式法:结合表格或关系式进行判断;
(3)经验法:借助积累的经验进行分析判断.
变式训练1 某地农业技术指导站的技术员,经过在7块并排大小相同的试验田上进行施化肥量对水稻产量影响的试验,得到如下表所示的一组数据:(单位:千克)
施化肥量x
15
20
25
30
35
40
45
水稻产量y
330
345
365
405
445
450
455
施化肥量x和水稻产量y是否具有相关关系?
解:作出散点图进行分析.散点图如下:
从散点图可以看出施化肥量x和水稻产量y的确存在一定相关关系,大体上随着施化肥量的增加,水稻的产量也在增加.
求回归直线方程
据最小二乘估计思想的公式,用待定系数法求出a,b,从而确定回归直线方程.
5个学生的数学和物理成绩(单位:分)如下表:
例2
学生
学科
A
B
C
D
E
数学
80
75
70
65
60
物理
70
66
68
64
62
画出散点图,判断它们是否具有相关关系,若相关,求出回归方程.
【解】 以x轴表示数学成绩,y轴表示物理成绩,可得到相应的散点图如图所示.
由散点图可知,两者之间具有相关关系,且为线性相关.
列表,计算
i
1
2
3
4
5
xi
80
75
70
65
60
yi
70
66
68
64
62
x i y i
5600
4950
4760
4160
3720
6400
5625
4900
4225
3600
变式训练2 随着我国经济的快速发展,城乡居民的生活水平不断提高,为研究某市家庭平均收入与月平均生活支出的关系,该市统计部门随机调查10个家庭,得数据如下表:
家庭编号
1
2
3
4
5
6
7
8
9
10
xi(收入)/千元
0.8
1.1
1.3
1.5
1.5
1.8
2.0
2.2
2.4
2.8
yi(支出)/千元
0.7
1.0
1.2
1.0
1.3
1.5
1.3
1.7
2.0
2.5
(1)判断家庭平均收入与月平均生活支出是否相关;
(2)若二者线性相关,求回归直线方程.
解:(1)作出散点图:
观察发现各个数据对应的点都在一条直线附近,所以二者有线性相关关系
利用回归直线,我们可以进行预测.若回归直线方程为y=bx+a,则x=x0处的估计值为:y=bx0+a.
某5名学生总成绩和数学成绩(单位:分)如下表所示:
利用回归方程对总体进行估计
例3
学生
A
B
C
D
E
总成绩(x)
482
383
421
364
362
数学成绩(y)
78
65
71
64
61
(1)作出散点图;
(2)求数学成绩y对总成绩x的回归方程;
(3)如果一个学生的总成绩为450分,试预测这个学生的数学成绩.
【思路点拨】 进行线性回归分析的关键是求出线性回归直线方程.由于求回归系数a、b的运算量很大,故可用列表法并借助计算器求解.
【解】 (1)散点图如图所示:
(2)列表:
i
1
2
3
4
5
xi
482
383
421
364
362
yi
78
65
71
64
61
x i y i
37596
24895
29891
23296
22082
【名师点评】 (1)回归分析是寻找相关关系中非确定性关系的某种确定性;
(2)求回归直线方程,关键在于正确地求出系数a,b,由于a,b的计算量大,计算时要仔细,避免计算失误.
变式训练3 一台机器由于使用时间较长,生产的零件有一些会缺损,按不同转速生产出来的零件有缺损的统计数据如下表:
转速x(转/秒)
16
14
12
8
每小时生产缺损零件数y(件)
11
9
8
5
(1)作出散点图;
(2)如果y与x线性相关,求出回归直线方程;
(3)若实际生产中,允许每小时的产品中有缺损的零件最多为10个,那么,机器的运转速度应控制在什么范围?
解:(1)根据表中的数据画出散点图如图:
(2)设回归直线方程为:y=bx+a,并列表如下:
i
1
2
3
4
xi
16
14
12
8
yi
11
9
8
5
xiyi
176
126
96
40
1.在研究两个变量是否存在某种关系时,必须从散点图入手,对于散点图,可以做出如下判断:(1)如果所有的样本点都落在某一函数曲线上,那么就用该函数来描述变量之间的关系,即变量之间具有函数关系;(2)如果所有的样本点都落在某一函数曲线附近,那么变量之间具有相关关系;(3)如果所有的样本点都落在某一直线附近,那么变量之间具有线性相关关系.
方法感悟
2.知道x与y呈线性相关关系,无需进行相关性检验,否则,应首先进行相关性检验,如果本身两个变量不具备相关关系,或者说,它们之间相关关系不显著,即使求出回归直线方程也是毫无意义的,而且用其估计和预测的量也是不可信的.
3.利用回归方程估计总体,只是反映了x与y的一种近似的相关关系,即y值并不一定是真实值.
同课章节目录
