13.2.2几何概率_课件1-湘教版数学必修5(24张PPT)
文档属性
| 名称 | 13.2.2几何概率_课件1-湘教版数学必修5(24张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 439.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-01 00:00:00 | ||
图片预览








文档简介
【课标要求】
1.了解几何概型的定义及其特点;了解几何概型与古典概型的区别.
2.会用几何概型的概率计算公式求几何概型的概率.
几何概率
1.几何概率1
设试验的全集Ω是长度为正数的区间,A是Ω的子区间.如果试验的结果随机地落在Ω中,则称P(A)= 为事件A的概率.
2.几何概率2
设试验的全集Ω是面积为正数的区域,A是Ω的子区域.如果元素随机地落在Ω中,则称P(A)= 为事件A的概率.
3.几何概率的基本性质
(1)0≤P(A)≤1;
(2)P(Ω)=1;P(?)=0;
(3)如果A,B互斥,则P(A∪B)= .
P(A)+P(A)
自主探究
1.几何概型的概率计算与构成事件的区域形状有关吗?
答案 几何概型的概率只与它的长度(面积或体积)有关,而与构成事件的区域形状无关.
2.概率为0的事件一定是不可能事件吗?概率为1的事件也一定是必然事件吗?
答案 如果随机事件所在区域是一个单点,因单点的长度、面积、体积均为0,则它出现的概率为0(即P=0),但它不是不可能事件;如果随机事件所在的区域是全部区域扣除一个单点,则它出现的概率为1(即P=1),但它不是必然事件.
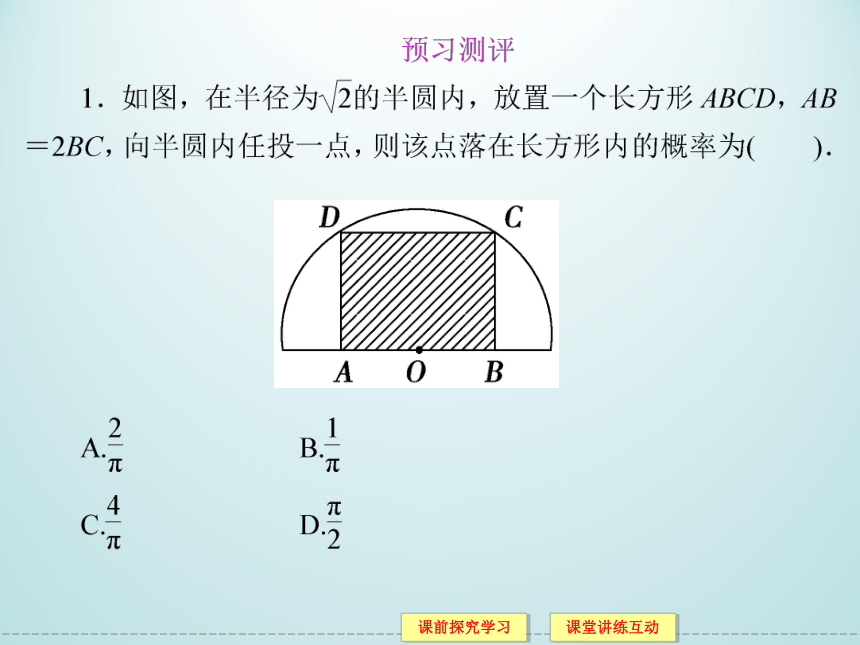
答案 A
2.手表实际上是个转盘,一天24小时,分针指向哪个数字的概率最大( ).
A.12 B.6
C.1 D.12个数字概率相同
解析 分针每天转24圈,指向每个数字的可能性是相同的,故指向12个数字的概率相同.
答案 D
3.水面直径为0.25 m的金鱼缸的水面上飘着一块面积为0.02 m2的浮草,则向缸里随机洒鱼食时,鱼食掉在浮草上的概率约为
( ).
A.0.101 9 B.0.203 8
C.0.407 6 D.0.025 5
答案 C
4.向图中所示正方形内随机地投掷飞镖,求飞镖落在阴影部分的概率( ).
答案 C
要点阐释
1.几何概型概率的适用情况和计算步骤
(1)适用情况:
几何概型用来计算事件发生的概率适用于有无限多个试验结果的情况,每种结果的出现也要求必须是等可能的.而且事件发生在一个有明确范围的区域中,其概率与构成该事件区域的长度(面积)成比例.
(2)计算步骤:
①判断是否是几何概率,尤其是判断等可能性,比古典概型更难于判断.
②计算基本事件空间与事件A所含的基本事件对应的区域的几何度量(长度或面积).这是计算的难点.
③利用概率公式计算.
2.几何概型的处理方法
有关几何概型的计算的首要任务是计算事件A包含的基本事件对应的区域的长度、角度、面积或体积,而这往往很困难,这是本节难点之一,实际上本节的重点不在于计算,而在于如何利用几何概型,把问题转化为各种几何概型问题,为此可以参考以下办法:①适当选择观察角度(原则是基本事件无限性、等可能性);②把基本事件转化为与之对应的区域;③把随机事件A转化为与之对应的区域;④利用概率公式给出计算;⑤如果事件A的对应区域不好处理,可以用对立事件概率公式逆向思考.
典例剖析
题型一 与长度有关的几何概型概率的求法
【例1】 平面上画了一些彼此平行且相距2a的平行线.把一枚半径r解 法一 设事件A:“硬币不与任一直线相碰”,为了确定硬币的位置,由硬币中心O向靠得最近的平行线引垂线OM,垂足为M,如图,显然OM的取值范围是[0,a],当线段OM的长度满足r法二 如图:在两相邻平行线间画出任意间距为r的两平行虚线.则当硬币中心落在两虚线间时,与平行线不相碰.
方法点评 本题中把硬币不与平行线相碰转化为圆心O到平行线的距离是关键,从而可方便地确定事件A的区域长度和所有可能结果的区域长度.将概率问题转化为几何问题来计算是几何概型的精华之所在.
1.国家安全机关监听录音机记录了两个间谍的谈话,发现30 min长的磁带上,从开始30 s处起,有10 s长的一段内容包含间谍犯罪的信息.后来发现,这段谈话的一部分被某工作人员擦掉了,该工作人员声称他完全是无意中按错了键,使从此处起往后的所有内容都被擦掉了.那么由于按错了键使含有犯罪内容的谈话被部分或全部擦掉的概率有多大?
题型二 与面积有关的几何概型概率的求法
【例2】 在一个大型商场的门口,有一种游戏是向一个画满边长为5 cm的均匀方格的大桌子上投直径为2 cm的硬币,如果硬币完全落入某个方格中,则掷硬币者赢得一瓶洗发水.请问随机掷一枚硬币正好完全落入某个格子的概率有多大?
解 如图边长为5的正方形形成的区域表示试验的所有基本事件构成的区域,当硬币的中心落入图中以3为边长的正方形区域时,则试验成功.所以,随机投一枚硬币正好完全落入某个格子的概率为:
方法点评 面积法求概率的步骤是,首先把事件转化为与之对应的区域,其次,求出相应区域的面积,最后利用面积比确定概率.
2.如图所示的矩形,长为5,宽为2.在矩形内随机地撒300颗黄豆,数得落在阴影部分的黄豆数为138颗.则我们可以估计出阴影部分的面积约为________.
误区警示 几何概型中的度量选错而致误
【例3】 在0~1之间随机选择两个数,这两个数对应的点把0~1之间的线段分成了三条,试求这三条线段能构成三角形的概率.
错因分析 误把长度为几何度量当本题的模型而致错.
在平面上建立如图所示的直角坐标系,直线x=0,x=1,y=-x+1围成如图所示的三角形区域G,每一对(x,y)对应着G内的点(x,y),
由题意知,每一个试验结果出现的可能性相等,因此,试验属于几何概型.
三条线段能构成三角形当且仅当
课堂总结
1.几何概型的计算步骤
(1)判断是否是几何概率,尤其是判断等可能性,比古典概型更难于判断.
(2)计算基本事件空间与事件A所含的基本事件对应的区域的几何度量(长度或面积).这是计算的难点.
(3)利用概率公式计算.
2.用随机数模拟的关键是把实际问题中事件A及基本事件总体对应的区域转化为随机数的范围.
1.了解几何概型的定义及其特点;了解几何概型与古典概型的区别.
2.会用几何概型的概率计算公式求几何概型的概率.
几何概率
1.几何概率1
设试验的全集Ω是长度为正数的区间,A是Ω的子区间.如果试验的结果随机地落在Ω中,则称P(A)= 为事件A的概率.
2.几何概率2
设试验的全集Ω是面积为正数的区域,A是Ω的子区域.如果元素随机地落在Ω中,则称P(A)= 为事件A的概率.
3.几何概率的基本性质
(1)0≤P(A)≤1;
(2)P(Ω)=1;P(?)=0;
(3)如果A,B互斥,则P(A∪B)= .
P(A)+P(A)
自主探究
1.几何概型的概率计算与构成事件的区域形状有关吗?
答案 几何概型的概率只与它的长度(面积或体积)有关,而与构成事件的区域形状无关.
2.概率为0的事件一定是不可能事件吗?概率为1的事件也一定是必然事件吗?
答案 如果随机事件所在区域是一个单点,因单点的长度、面积、体积均为0,则它出现的概率为0(即P=0),但它不是不可能事件;如果随机事件所在的区域是全部区域扣除一个单点,则它出现的概率为1(即P=1),但它不是必然事件.
答案 A
2.手表实际上是个转盘,一天24小时,分针指向哪个数字的概率最大( ).
A.12 B.6
C.1 D.12个数字概率相同
解析 分针每天转24圈,指向每个数字的可能性是相同的,故指向12个数字的概率相同.
答案 D
3.水面直径为0.25 m的金鱼缸的水面上飘着一块面积为0.02 m2的浮草,则向缸里随机洒鱼食时,鱼食掉在浮草上的概率约为
( ).
A.0.101 9 B.0.203 8
C.0.407 6 D.0.025 5
答案 C
4.向图中所示正方形内随机地投掷飞镖,求飞镖落在阴影部分的概率( ).
答案 C
要点阐释
1.几何概型概率的适用情况和计算步骤
(1)适用情况:
几何概型用来计算事件发生的概率适用于有无限多个试验结果的情况,每种结果的出现也要求必须是等可能的.而且事件发生在一个有明确范围的区域中,其概率与构成该事件区域的长度(面积)成比例.
(2)计算步骤:
①判断是否是几何概率,尤其是判断等可能性,比古典概型更难于判断.
②计算基本事件空间与事件A所含的基本事件对应的区域的几何度量(长度或面积).这是计算的难点.
③利用概率公式计算.
2.几何概型的处理方法
有关几何概型的计算的首要任务是计算事件A包含的基本事件对应的区域的长度、角度、面积或体积,而这往往很困难,这是本节难点之一,实际上本节的重点不在于计算,而在于如何利用几何概型,把问题转化为各种几何概型问题,为此可以参考以下办法:①适当选择观察角度(原则是基本事件无限性、等可能性);②把基本事件转化为与之对应的区域;③把随机事件A转化为与之对应的区域;④利用概率公式给出计算;⑤如果事件A的对应区域不好处理,可以用对立事件概率公式逆向思考.
典例剖析
题型一 与长度有关的几何概型概率的求法
【例1】 平面上画了一些彼此平行且相距2a的平行线.把一枚半径r
方法点评 本题中把硬币不与平行线相碰转化为圆心O到平行线的距离是关键,从而可方便地确定事件A的区域长度和所有可能结果的区域长度.将概率问题转化为几何问题来计算是几何概型的精华之所在.
1.国家安全机关监听录音机记录了两个间谍的谈话,发现30 min长的磁带上,从开始30 s处起,有10 s长的一段内容包含间谍犯罪的信息.后来发现,这段谈话的一部分被某工作人员擦掉了,该工作人员声称他完全是无意中按错了键,使从此处起往后的所有内容都被擦掉了.那么由于按错了键使含有犯罪内容的谈话被部分或全部擦掉的概率有多大?
题型二 与面积有关的几何概型概率的求法
【例2】 在一个大型商场的门口,有一种游戏是向一个画满边长为5 cm的均匀方格的大桌子上投直径为2 cm的硬币,如果硬币完全落入某个方格中,则掷硬币者赢得一瓶洗发水.请问随机掷一枚硬币正好完全落入某个格子的概率有多大?
解 如图边长为5的正方形形成的区域表示试验的所有基本事件构成的区域,当硬币的中心落入图中以3为边长的正方形区域时,则试验成功.所以,随机投一枚硬币正好完全落入某个格子的概率为:
方法点评 面积法求概率的步骤是,首先把事件转化为与之对应的区域,其次,求出相应区域的面积,最后利用面积比确定概率.
2.如图所示的矩形,长为5,宽为2.在矩形内随机地撒300颗黄豆,数得落在阴影部分的黄豆数为138颗.则我们可以估计出阴影部分的面积约为________.
误区警示 几何概型中的度量选错而致误
【例3】 在0~1之间随机选择两个数,这两个数对应的点把0~1之间的线段分成了三条,试求这三条线段能构成三角形的概率.
错因分析 误把长度为几何度量当本题的模型而致错.
在平面上建立如图所示的直角坐标系,直线x=0,x=1,y=-x+1围成如图所示的三角形区域G,每一对(x,y)对应着G内的点(x,y),
由题意知,每一个试验结果出现的可能性相等,因此,试验属于几何概型.
三条线段能构成三角形当且仅当
课堂总结
1.几何概型的计算步骤
(1)判断是否是几何概率,尤其是判断等可能性,比古典概型更难于判断.
(2)计算基本事件空间与事件A所含的基本事件对应的区域的几何度量(长度或面积).这是计算的难点.
(3)利用概率公式计算.
2.用随机数模拟的关键是把实际问题中事件A及基本事件总体对应的区域转化为随机数的范围.
同课章节目录
