13.3频率与概率_课件1(1)-湘教版数学必修5(30张PPT)
文档属性
| 名称 | 13.3频率与概率_课件1(1)-湘教版数学必修5(30张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 733.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-01 00:00:00 | ||
图片预览










文档简介
频率与概率
频
率
与
概
率
课堂互动讲练
课前自主学案
学习目标
1.通过实例,进一步理解概率的意义;
2.会用概率的意义解释生活中的实例;
3.了解用模拟方法估计概率的实质,会用模拟方法估计概率.
课前自主学案
1.事件A理解为区域Ω的某一子区域A,A的概率只与子区域A的几何度量(_______、
_______等)成正比,而与A的形状无关,满足以上条件的试验称为几何概率.
2.几何概率的特征:________、
___________
温故夯基
长度
面积
无限性
等可能性.
知新益能
1.概率
(1)含义:概率是度量随机事件发生的
____________________的量.
(2)与频率联系:对于给定的随机事件A,事件A发生的_________随着试验次数的增加稳定于_______,因此可以用__________来估计
______________
2.模拟试验
用计算机或计算器模拟试验的方法.
可能性大小
频率fN
P(A)
频率fN
概率P(A).
连续两周,每周的周五都下雨,能够断定第三周的周五还要下雨吗?
提示:不能断定.因为周五下雨是一种随机事件,而不是必然事件.
问题探究
课堂互动讲练
频率与概率的关系
考点突破
随机事件的频率在每次试验中都可能会有不同的结果,但它具有一定的稳定性.概率是频率的稳定值,是频率的科学抽象,不会随试验次数的变化而变化.
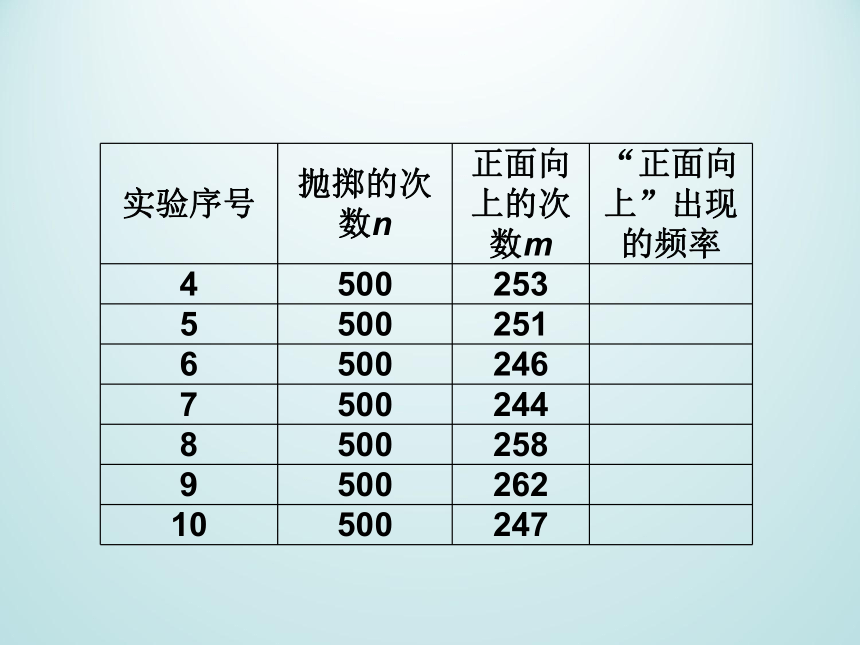
下面的表中列出10次抛掷硬币的试验结果.n为抛掷硬币的次数,m为硬币正面向上的次数.计算每次试验中“正面向上”这一事件的频率,并考查它的概率.
例1
实验序号
抛掷的次数n
正面向上的次数m
“正面向上”出现的频率
1
500
251
2
500
249
3
500
256
实验序号
抛掷的次数n
正面向上的次数m
“正面向上”出现的频率
4
500
253
5
500
251
6
500
246
7
500
244
8
500
258
9
500
262
10
500
247
【思路点拨】 频率是事件发生的次数m与试验次数n的比值,利用此公式可求出它们的频率.
【名师点评】 频率本身是随机变量,当n很大时,频率总在一个稳定值附近左右摆动,这个稳定值就是概率.
变式训练1 某篮球运动员在最近几场大赛中罚球投篮的结果如下:
投篮次数n
8
10
12
9
10
16
进球次数m
6
8
9
7
7
12
进球频率
(1)计算表中进球的频率;
(2)这位运动员投篮一次进球的概率是多少?
解:(1)进球的频率依次是
0.75,0.80,0.75,0.78,0.70,0.75.
(2)这位运动员投篮一次进球的概率P≈0.76.
正确理解概率的意义
随机事件在一次试验中发生与否是随机的,但随机中含有规律性,而概率恰是其规律性在数量上的反映,概率是客观存在的,它与试验次数,哪一个具体的试验都没有关系,运用概率知识,可以帮助我们澄清日常生活中人们对一些现象的错误认识.
某种病治愈的概率是0.3,那么前7个人没有治愈,后3个人一定能治愈吗?如何理解治愈的概率是0.3?
【思路点拨】 正确理解随机事件概率的意义,纠正日常生活中出现的一些错误认识是解决本题的关键.
例2
【解】 不一定.如果把治疗一个病人作为一次试验,“治愈的概率是0.3”指随着试验次数的增加,即治疗人数的增加,大约有30%的人能够治愈,对于一次试验来说,其结果是随机的,因此前7个病人没有治愈是可能的,对后3个人来说,其结果仍然是随机的,有可能治愈,也可能没有治愈.
治愈的概率是0.3,指如果患病的人有1000人,那么我们根据治愈的频率应在治愈的概率附近摆动这一前提,就可以认为这1000个人中大约有300人能治愈.
【名师点评】 概率是用来度量随机事件发生可能性大小的一个量,而实际结果是事件发生与不发生这两种情况中的一种.
(3)某市气象预报说:“明天本市降雨的概率为60%”.有人认为明天本市有60%的区域要下雨,40%的区域不下雨;也有人认为明天本市有60%的时间下雨,有40%的时间不下雨.
以上说法对吗?
(3)不对.
明天本市降雨的概率为60%,是指本市明天下雨的可能性为60%.不是指下雨的区域,也不是下雨的时间.
用频率估计概率时,需做大量的重复试验,费时费力,并且有些试验具有破坏性,有些试验无法进行,因而随机模拟试验就成为一种重要的方法,它可以在短时间内多次重复.通过设计模拟试验,利用计算器或计算机产生随机数,通过随机数的特征来估计概率,这一方法在很多科学试验中都有广泛的应用.
用随机模拟法估计概率
某篮球爱好者做投篮练习,假设其每次投篮命中的概率是60%,那么在连续三次投篮中,三次都投中的概率是多少?
例3
【解】 我们通过设计模拟试验的方法来解决问题,利用计算机或计算器可以产生0到9之间的取整数值的随机数.
我们用1,2,3,4,5,6表示投中,用7,8,9,0表示未投中,这样可以体现投中的概率是60%.因为是投篮三次,所以每三个随机数作为一组.
例如:产生20组随机数:
812 932 569 683 271
989 730 537 925 834
907 113 966 191 432
256 393 027 556 755
【名师点评】 (1)由于该投篮者投篮的结果不是等可能出现的,故不能用古典概型的概率公式计算,只能用模拟试验来估算其概率.
(2)这种用模拟试验来求概率的方法所得结果是不精确的,且每次模拟最终得到的概率值不一定是相同的.
变式训练3 种植某种树苗,成活率是0.9,若种植这种树苗5棵,求恰有4棵成活的概率.
解:利用计算器或计算机产生0到9之间取整数值的随机数,我们用0代表不成活,1至9的数字代表成活,这样可以体现成活率是0.9.因为是种植5棵,所以每5个随机数作为一组,可产生30组随机数.
________ ________ 77124 22961
74235 31516 29747 24945
57558 65258 _______ 23224
37445 44344 33315 __________
21782 58555 _______ 45241
44134 _________ ________ 83005
94976 56173 34783 16624
________ __________
69801
66097
74130
27120
61017
92201
70362
30344
01117
方法感悟
1.频率是概率的近似值,随着试验次数的增加,频率会越来越接近概率,在实际问题中,常用事件发生的频率作为概率的估计值,频率本身是随机的,而概率是一个确定的数,是客观存在的,因此概率与每次试验无关.
2.概率是从数量上反映了随机事件发生的可能性大小的一个数学概念,它是对大量重复试验来说存在的一种统计规律性,对单次试验来说,随机事件发生与否是随机的.
3.用计算器或计算机产生整数值随机数的模拟试验,不仅可以用来求古典概型概率的近似值,还可以用来求一些非古典概型概率的近似值,但都要设计恰当的试验方案,并且使试验次数尽可能多,这样才与实际概率十分接近.
频
率
与
概
率
课堂互动讲练
课前自主学案
学习目标
1.通过实例,进一步理解概率的意义;
2.会用概率的意义解释生活中的实例;
3.了解用模拟方法估计概率的实质,会用模拟方法估计概率.
课前自主学案
1.事件A理解为区域Ω的某一子区域A,A的概率只与子区域A的几何度量(_______、
_______等)成正比,而与A的形状无关,满足以上条件的试验称为几何概率.
2.几何概率的特征:________、
___________
温故夯基
长度
面积
无限性
等可能性.
知新益能
1.概率
(1)含义:概率是度量随机事件发生的
____________________的量.
(2)与频率联系:对于给定的随机事件A,事件A发生的_________随着试验次数的增加稳定于_______,因此可以用__________来估计
______________
2.模拟试验
用计算机或计算器模拟试验的方法.
可能性大小
频率fN
P(A)
频率fN
概率P(A).
连续两周,每周的周五都下雨,能够断定第三周的周五还要下雨吗?
提示:不能断定.因为周五下雨是一种随机事件,而不是必然事件.
问题探究
课堂互动讲练
频率与概率的关系
考点突破
随机事件的频率在每次试验中都可能会有不同的结果,但它具有一定的稳定性.概率是频率的稳定值,是频率的科学抽象,不会随试验次数的变化而变化.
下面的表中列出10次抛掷硬币的试验结果.n为抛掷硬币的次数,m为硬币正面向上的次数.计算每次试验中“正面向上”这一事件的频率,并考查它的概率.
例1
实验序号
抛掷的次数n
正面向上的次数m
“正面向上”出现的频率
1
500
251
2
500
249
3
500
256
实验序号
抛掷的次数n
正面向上的次数m
“正面向上”出现的频率
4
500
253
5
500
251
6
500
246
7
500
244
8
500
258
9
500
262
10
500
247
【思路点拨】 频率是事件发生的次数m与试验次数n的比值,利用此公式可求出它们的频率.
【名师点评】 频率本身是随机变量,当n很大时,频率总在一个稳定值附近左右摆动,这个稳定值就是概率.
变式训练1 某篮球运动员在最近几场大赛中罚球投篮的结果如下:
投篮次数n
8
10
12
9
10
16
进球次数m
6
8
9
7
7
12
进球频率
(1)计算表中进球的频率;
(2)这位运动员投篮一次进球的概率是多少?
解:(1)进球的频率依次是
0.75,0.80,0.75,0.78,0.70,0.75.
(2)这位运动员投篮一次进球的概率P≈0.76.
正确理解概率的意义
随机事件在一次试验中发生与否是随机的,但随机中含有规律性,而概率恰是其规律性在数量上的反映,概率是客观存在的,它与试验次数,哪一个具体的试验都没有关系,运用概率知识,可以帮助我们澄清日常生活中人们对一些现象的错误认识.
某种病治愈的概率是0.3,那么前7个人没有治愈,后3个人一定能治愈吗?如何理解治愈的概率是0.3?
【思路点拨】 正确理解随机事件概率的意义,纠正日常生活中出现的一些错误认识是解决本题的关键.
例2
【解】 不一定.如果把治疗一个病人作为一次试验,“治愈的概率是0.3”指随着试验次数的增加,即治疗人数的增加,大约有30%的人能够治愈,对于一次试验来说,其结果是随机的,因此前7个病人没有治愈是可能的,对后3个人来说,其结果仍然是随机的,有可能治愈,也可能没有治愈.
治愈的概率是0.3,指如果患病的人有1000人,那么我们根据治愈的频率应在治愈的概率附近摆动这一前提,就可以认为这1000个人中大约有300人能治愈.
【名师点评】 概率是用来度量随机事件发生可能性大小的一个量,而实际结果是事件发生与不发生这两种情况中的一种.
(3)某市气象预报说:“明天本市降雨的概率为60%”.有人认为明天本市有60%的区域要下雨,40%的区域不下雨;也有人认为明天本市有60%的时间下雨,有40%的时间不下雨.
以上说法对吗?
(3)不对.
明天本市降雨的概率为60%,是指本市明天下雨的可能性为60%.不是指下雨的区域,也不是下雨的时间.
用频率估计概率时,需做大量的重复试验,费时费力,并且有些试验具有破坏性,有些试验无法进行,因而随机模拟试验就成为一种重要的方法,它可以在短时间内多次重复.通过设计模拟试验,利用计算器或计算机产生随机数,通过随机数的特征来估计概率,这一方法在很多科学试验中都有广泛的应用.
用随机模拟法估计概率
某篮球爱好者做投篮练习,假设其每次投篮命中的概率是60%,那么在连续三次投篮中,三次都投中的概率是多少?
例3
【解】 我们通过设计模拟试验的方法来解决问题,利用计算机或计算器可以产生0到9之间的取整数值的随机数.
我们用1,2,3,4,5,6表示投中,用7,8,9,0表示未投中,这样可以体现投中的概率是60%.因为是投篮三次,所以每三个随机数作为一组.
例如:产生20组随机数:
812 932 569 683 271
989 730 537 925 834
907 113 966 191 432
256 393 027 556 755
【名师点评】 (1)由于该投篮者投篮的结果不是等可能出现的,故不能用古典概型的概率公式计算,只能用模拟试验来估算其概率.
(2)这种用模拟试验来求概率的方法所得结果是不精确的,且每次模拟最终得到的概率值不一定是相同的.
变式训练3 种植某种树苗,成活率是0.9,若种植这种树苗5棵,求恰有4棵成活的概率.
解:利用计算器或计算机产生0到9之间取整数值的随机数,我们用0代表不成活,1至9的数字代表成活,这样可以体现成活率是0.9.因为是种植5棵,所以每5个随机数作为一组,可产生30组随机数.
________ ________ 77124 22961
74235 31516 29747 24945
57558 65258 _______ 23224
37445 44344 33315 __________
21782 58555 _______ 45241
44134 _________ ________ 83005
94976 56173 34783 16624
________ __________
69801
66097
74130
27120
61017
92201
70362
30344
01117
方法感悟
1.频率是概率的近似值,随着试验次数的增加,频率会越来越接近概率,在实际问题中,常用事件发生的频率作为概率的估计值,频率本身是随机的,而概率是一个确定的数,是客观存在的,因此概率与每次试验无关.
2.概率是从数量上反映了随机事件发生的可能性大小的一个数学概念,它是对大量重复试验来说存在的一种统计规律性,对单次试验来说,随机事件发生与否是随机的.
3.用计算器或计算机产生整数值随机数的模拟试验,不仅可以用来求古典概型概率的近似值,还可以用来求一些非古典概型概率的近似值,但都要设计恰当的试验方案,并且使试验次数尽可能多,这样才与实际概率十分接近.
同课章节目录
