2021-2022学年人教版数学 九年级上册24.4.1弧长和扇形面积 课件(共21张ppt)
文档属性
| 名称 | 2021-2022学年人教版数学 九年级上册24.4.1弧长和扇形面积 课件(共21张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-01 21:49:14 | ||
图片预览






文档简介
九年级上册 第二十四章 圆
九年级数学备课组
24.4.1弧长和扇形面积
(第一课时)
我们学校马上要进行冬季运动会了,每年冬季运动会都会有二百米跑步比赛,同学们想一想在比赛中每位同学的起跑位置相同吗?这样做公平吗?每位同学跑过的长度相同吗?
情境导入
学习任务单问题呈现
1
2
3
1.什么是弧?
2.半径为R的圆的周长公式是_______。
3.半径为R的圆的面积公式是_______。
课前回顾
学习目标
1.会推导弧长公式和扇形面积公式并能用公式解决相关问题;
2.会求不规则图形阴影部分的面积并能写出完整解题过程.
n°
A
B
O
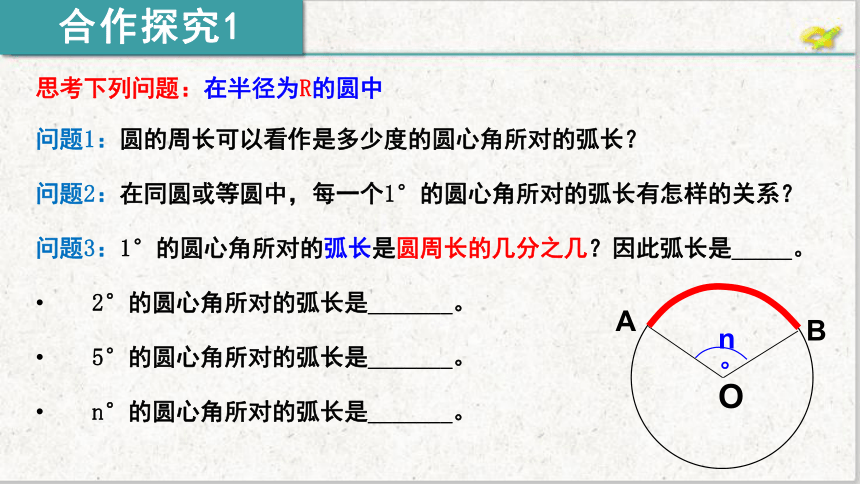
思考下列问题:在半径为R的圆中
问题1:圆的周长可以看作是多少度的圆心角所对的弧长?
问题2:在同圆或等圆中,每一个1°的圆心角所对的弧长有怎样的关系?
问题3:1°的圆心角所对的弧长是圆周长的几分之几?因此弧长是_____。
2°的圆心角所对的弧长是_______。
5°的圆心角所对的弧长是_______。
n°的圆心角所对的弧长是_______。
合作探究1
在半径为 R 的圆中,n0 的圆心角所对的弧长为:
理解记忆弧长公式:
思考:(1)公式中的n表示什么意思?
(2)弧长的大小由哪些量决定?
在弧长公式 中,n表示1°的圆心角的倍数,n和180都不带单位。
讨论点拨1
1.已知弧所对的圆心角为900,半径是4,则弧长为( )
A. B. C. D.
2. 已知一条弧的半径为9,弧长为8 ,那么这条弧所对的圆心角为 ( )
A. 400 B. 900 C. 1200 D. 1600
小结:弧长公式中出现的三个量 l ,n,R,只要已知其中任意两个量,就能求出第三个量。
3.已知1000的圆心角所对的弧长为5 ,则该圆的半径为_______。
当堂训练1
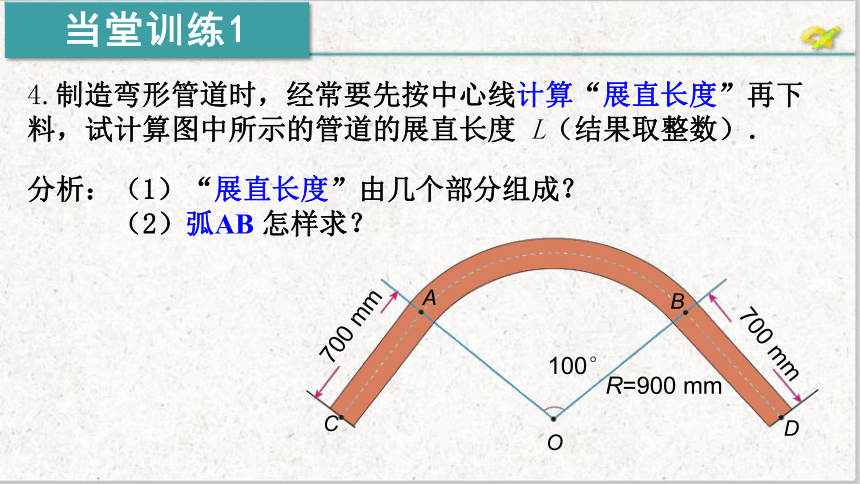
4.制造弯形管道时,经常要先按中心线计算“展直长度”再下料,试计算图中所示的管道的展直长度 L(结果取整数).
A
B
C
D
O
R=900 mm
700 mm
700 mm
100°
分析:(1)“展直长度”由几个部分组成?
(2)弧AB 怎样求?
当堂训练1
由组成圆心角的两条半径和圆心角所对的弧围成的图形叫做扇形。
什么是扇形?
A
B
O
思考:
(1)扇形与圆有什么关系?
(2)扇形的面积与圆的面积有什么关系?
合作探究2
类比弧长公式的推导:在半径为R的圆中
1、圆的面积公式是 _______。
2、圆的面积可以看作_______度圆心角所对的扇形的面积;
1°的圆心角所对的扇形面积S扇形=_______。
2°的圆心角所对的扇形面积S扇形=_______。
5°的圆心角所对的扇形面积S扇形=_______。
n°的圆心角所对的扇形面积S扇形=_______。
合作探究2
在半径为 R 的圆中,圆心角为 n0 的扇形的面积是:
问题:比较扇形面积公式和弧长公式,你能用弧长表示扇形面积吗?
想一想:扇形的面积公式与什么公式类似?
讨论点拨2
1、已知扇形的圆心角为120°,半径为2,则这个扇形
的面积S扇形= .
3、已知半径为2cm的扇形,其弧长为 ,则这个扇
形的面积S扇形= .
2、已知扇形面积为 ,圆心角为60°,则这个扇形的
半径R= .
当堂训练2
例:如图,水平放置的圆柱形排水管道的截面半径是0.6 m,其中水面高 0.3 m,求截面上有水部分的面积.
分析:(1)截面上有水部分的图形是什么形状?能用公式直接计算面积吗?
(2)对于不规则图形面积计算我们一般怎么处理?
(3)对于该图我们怎么割补,请在图中画出辅助线,并标出半径0.6m和水高0.3m?
O
A
B
C
D
(4)要求扇形AOB和 的面积需知道哪些量?
典型例题讲解
解:如图连接OA、OB,过点O作弦AB的垂线,垂足为D,交弧AB于点C,连接AC。
S弓形=S扇形-S三角形
S弓形=S扇形+S三角形
0
0
弓形的面积是扇形的面积与三角形
面积的和或差
经验分享
求阴影部分的面积是中考的一个高频考点:
求不规则图形的面积,常常采用割补法,把不规则图形转化为规则图形来求面积。
求面积实际上转化为求线段的长度或角度,在圆当中常常采用垂径定理、勾股定理、等腰三角形和等边三角形的性质等知识相结合来解决。
经验分享
变式:如图、水平放置的圆柱形排水管道的截面半径是0.6cm,其中水面高0.9cm,求截面上有水部分的面积。
0
A
B
D
C
E
当堂训练2
1、弧长和扇形面积公式是什么?你是如何得到这两个公式的?
2、弧长与圆周长、扇形面积与圆面积之间有什么联系?
课堂小结
课后提升
(一)本节的提升作业:《名校课堂》P91-92
(二)预习下一节任务单
海浪的品格,就是无数次被礁石击
碎又无数闪地扑向礁石!
九年级数学备课组
24.4.1弧长和扇形面积
(第一课时)
我们学校马上要进行冬季运动会了,每年冬季运动会都会有二百米跑步比赛,同学们想一想在比赛中每位同学的起跑位置相同吗?这样做公平吗?每位同学跑过的长度相同吗?
情境导入
学习任务单问题呈现
1
2
3
1.什么是弧?
2.半径为R的圆的周长公式是_______。
3.半径为R的圆的面积公式是_______。
课前回顾
学习目标
1.会推导弧长公式和扇形面积公式并能用公式解决相关问题;
2.会求不规则图形阴影部分的面积并能写出完整解题过程.
n°
A
B
O
思考下列问题:在半径为R的圆中
问题1:圆的周长可以看作是多少度的圆心角所对的弧长?
问题2:在同圆或等圆中,每一个1°的圆心角所对的弧长有怎样的关系?
问题3:1°的圆心角所对的弧长是圆周长的几分之几?因此弧长是_____。
2°的圆心角所对的弧长是_______。
5°的圆心角所对的弧长是_______。
n°的圆心角所对的弧长是_______。
合作探究1
在半径为 R 的圆中,n0 的圆心角所对的弧长为:
理解记忆弧长公式:
思考:(1)公式中的n表示什么意思?
(2)弧长的大小由哪些量决定?
在弧长公式 中,n表示1°的圆心角的倍数,n和180都不带单位。
讨论点拨1
1.已知弧所对的圆心角为900,半径是4,则弧长为( )
A. B. C. D.
2. 已知一条弧的半径为9,弧长为8 ,那么这条弧所对的圆心角为 ( )
A. 400 B. 900 C. 1200 D. 1600
小结:弧长公式中出现的三个量 l ,n,R,只要已知其中任意两个量,就能求出第三个量。
3.已知1000的圆心角所对的弧长为5 ,则该圆的半径为_______。
当堂训练1
4.制造弯形管道时,经常要先按中心线计算“展直长度”再下料,试计算图中所示的管道的展直长度 L(结果取整数).
A
B
C
D
O
R=900 mm
700 mm
700 mm
100°
分析:(1)“展直长度”由几个部分组成?
(2)弧AB 怎样求?
当堂训练1
由组成圆心角的两条半径和圆心角所对的弧围成的图形叫做扇形。
什么是扇形?
A
B
O
思考:
(1)扇形与圆有什么关系?
(2)扇形的面积与圆的面积有什么关系?
合作探究2
类比弧长公式的推导:在半径为R的圆中
1、圆的面积公式是 _______。
2、圆的面积可以看作_______度圆心角所对的扇形的面积;
1°的圆心角所对的扇形面积S扇形=_______。
2°的圆心角所对的扇形面积S扇形=_______。
5°的圆心角所对的扇形面积S扇形=_______。
n°的圆心角所对的扇形面积S扇形=_______。
合作探究2
在半径为 R 的圆中,圆心角为 n0 的扇形的面积是:
问题:比较扇形面积公式和弧长公式,你能用弧长表示扇形面积吗?
想一想:扇形的面积公式与什么公式类似?
讨论点拨2
1、已知扇形的圆心角为120°,半径为2,则这个扇形
的面积S扇形= .
3、已知半径为2cm的扇形,其弧长为 ,则这个扇
形的面积S扇形= .
2、已知扇形面积为 ,圆心角为60°,则这个扇形的
半径R= .
当堂训练2
例:如图,水平放置的圆柱形排水管道的截面半径是0.6 m,其中水面高 0.3 m,求截面上有水部分的面积.
分析:(1)截面上有水部分的图形是什么形状?能用公式直接计算面积吗?
(2)对于不规则图形面积计算我们一般怎么处理?
(3)对于该图我们怎么割补,请在图中画出辅助线,并标出半径0.6m和水高0.3m?
O
A
B
C
D
(4)要求扇形AOB和 的面积需知道哪些量?
典型例题讲解
解:如图连接OA、OB,过点O作弦AB的垂线,垂足为D,交弧AB于点C,连接AC。
S弓形=S扇形-S三角形
S弓形=S扇形+S三角形
0
0
弓形的面积是扇形的面积与三角形
面积的和或差
经验分享
求阴影部分的面积是中考的一个高频考点:
求不规则图形的面积,常常采用割补法,把不规则图形转化为规则图形来求面积。
求面积实际上转化为求线段的长度或角度,在圆当中常常采用垂径定理、勾股定理、等腰三角形和等边三角形的性质等知识相结合来解决。
经验分享
变式:如图、水平放置的圆柱形排水管道的截面半径是0.6cm,其中水面高0.9cm,求截面上有水部分的面积。
0
A
B
D
C
E
当堂训练2
1、弧长和扇形面积公式是什么?你是如何得到这两个公式的?
2、弧长与圆周长、扇形面积与圆面积之间有什么联系?
课堂小结
课后提升
(一)本节的提升作业:《名校课堂》P91-92
(二)预习下一节任务单
海浪的品格,就是无数次被礁石击
碎又无数闪地扑向礁石!
同课章节目录
