2021-2022学年湘教版数学八年级上册4.5.2一元一次不等式组的应用 课件(共21张PPT)
文档属性
| 名称 | 2021-2022学年湘教版数学八年级上册4.5.2一元一次不等式组的应用 课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 915.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-01 21:19:21 | ||
图片预览







文档简介
第2课时 一元一次不等式组的应用
第四章 一元一次不等式(组)
第5节 一元一次不等式组
学习目标
课时讲解
1
方案问题
课时导入
复习提问
引出问题
复习提问
引出问题
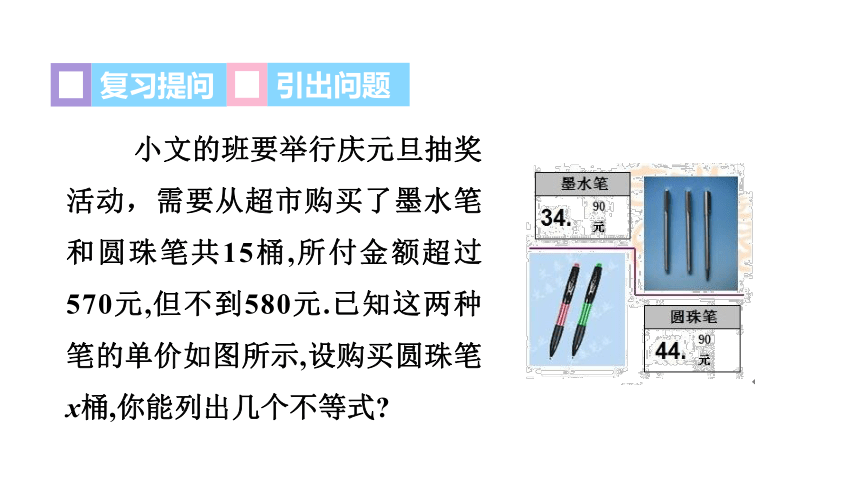
小文的班要举行庆元旦抽奖活动,需要从超市购买了墨水笔和圆珠笔共15桶,所付金额超过570元,但不到580元.已知这两种笔的单价如图所示,设购买圆珠笔x桶,你能列出几个不等式?
应用
方案问题
感悟新知
1
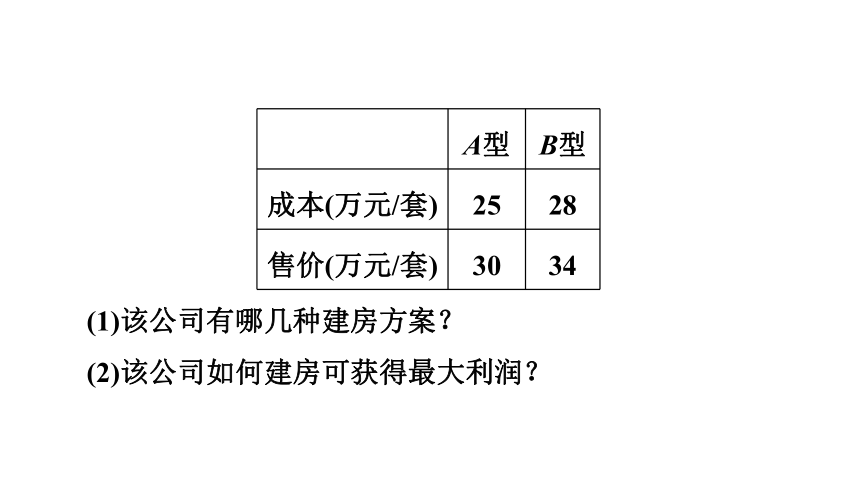
某房地产开发公司计划建A、B两种户型的住房共80套.
该公司所筹资金不少于2090万元,但不超过2096万元,且所筹资金全部用于建房,两种户型的建房成本和售价如下表:
例 1
感悟新知
{5940675A-B579-460E-94D1-54222C63F5DA}
A型
B型
成本(万元/套)
25
28
售价(万元/套)
30
34
(1)该公司有哪几种建房方案?
(2)该公司如何建房可获得最大利润?
感悟新知
导引:本题中的不等关系为:建房资金不少于2090万元,不超过2096万元,可根据它们建立不等式组,即A型住房成本+B型住房成本22 090万元;A型住房成本+B型住房成本≤2 096万元.
感悟新知
解:(1)设建A型住房x套,则建B型住房(80-x)套.
根据题意,得
解得48≤x≤50.
因为x为整数,所以x=48,49,50.
所以有三种建房方案.
方案一:A型48套,B型32套;
方案二:A型49套,B型31套;
方案三:A型50套,B型30套.
感悟新知
(2)第一种方案获利:48 x(30-25)+32 x(34-28)=432(万元);第二种方案获利:49 x(30-25)+31 x(34-28)=431(万元);
第三种方案获利:50 x(30-25)+30 x(34-28)=430(万元).
所以选方案一获利最大.
总 结
感悟新知
求实际问题中方案的种类或最大值(最小值)问题时,常通过求不等式(组)的解集,分类讨论找出答案,即先根据题意设出未知数,列出不等式(组),求出相应的取值范围,再根据题目的条件分类讨论,写出答案.
1.某汽车租赁公司要购买轿车和面包车共10辆,其中轿车至少要购买3辆,轿车每辆7万元,面包车每辆4万元,公司可投入的购车款不超过55万元.
(1)符合公司要求的购车方案有哪几种?请说明理由;
(2)如果每辆轿车的日租金为200元,每辆面包车的日租金为110元,假设新购买的这10辆车每日都可租出,要使这10辆车的日租金收入不低于1 500元,那么应选择(1)中的哪种购车方案?
感悟新知
感悟新知
解析:设购买轿车x辆,由购买轿车和面包车共10辆,可知购买面包车(10-x)辆.购车款不超过55万元,即小于或等于55万元,所以可列不等式7x+4(10-x)≤55,考虑到实际情况,x只能取非负整数.
感悟新知
解:(1)设轿车要购买x辆,那么面包车要购买(10-x)辆.由题意,得7x+4(10-x)≤55,解得x≤5.因轿车至少要购买3辆,所以x≥3,且x为整数.所以x=3或x=4或x=5.所以购车方案有三种:方案一:轿车购买3辆,面包车购买7辆;方案二:轿车购买4辆,面包车购买6辆;方案三:轿车购买5辆,面包车购买5辆.
感悟新知
(2)方案一的日租金为3×200+7×110=1370(元);方案二的日租金为4×200+6×110=1460(元);方案三的日租金为5×200+5×110=1550(元).为保证日租金不低于1500元,应选择方案三.
感悟新知
例2
某学校为开展“阳光体育”活动,计划拿出不超过3000元的资金购买一批篮球、羽毛球拍和乒乓球拍,已知篮球、羽毛球拍和乒乓球拍的单价比为8:3:2,且其单价和为130元.
(1)请问篮球、羽毛球拍和乒乓球拍的单价分别是多少元?
(2)若要求购买篮球、羽毛球拍和乒乓球拍的总数量是80个(副),羽毛球拍的数量是篮球数量的4倍,且购买乒乓球拍的数量不超过15副,请问有几种购买方案?
感悟新知
导引:(1)已知篮球、羽毛球拍和乒乓球拍的单价比为8:3:2,且其单价和为130元,可以设它们的单价分别为8x元、3x元、2x元,列一元一次方程来解决问题;
(2)根据购买丘乓球拍的数量不超过15副和用不超过3 000元的资金购买一批篮球、羽毛球拍和乒乓球拍这两个不等关系列不等式组,求出购买篮球数量的范围,从而确定购买方案.
感悟新知
解:(1)因为篮球、羽毛球拍和乒乓球拍的单价比为8:3:2,所以,可设它们的单价分别为8x元、3x元、2x元,于是,得8x+3x+2x=130,解得x=10,所以,篮球、羽毛球拍和乒乓球拍的单价分别为80元、
30元和20元.
感悟新知
(2)设购买篮球的数量为y个,则购买羽毛球拍的数量为4y副,购买乒乓球拍的数量为(80-y-4y)副,根据题意,得
解不等式①.得y≤14.解不等式⑤,得y≥13.
于是,不等式组的解集为13≤y≤14.
感悟新知
因为y取整数,所以,只能取13或14.
因此,一共有两种购买方案:方案一:当y=13时,篮球购买13个,羽毛球拍购买52副,丘乓球拍购买15副;方案二:当y=14时,篮球购买14个,羽毛球拍购买56副,乒乓球拍购买10副.
感悟新知
总 结
解决这类问题的关键是在理解题意的基础上寻找明显或隐含的等量关系或不等关系,准确列出方程(组)或不等式(组).
课堂小结
利用不等式组解实际问题的关键是找出题目中所有的不等关系,列出不等式组,再解不等式组,最后根据实际情况确定合理的答案,解题时要注意两点:
(1)设未知数时,要将“不少于"不超过”等词语换成确定性词语.
(2)答案要满足两个条件:①符合题目要求:②符合实际情况
一元一次不等式组的应用
第四章 一元一次不等式(组)
第5节 一元一次不等式组
学习目标
课时讲解
1
方案问题
课时导入
复习提问
引出问题
复习提问
引出问题
小文的班要举行庆元旦抽奖活动,需要从超市购买了墨水笔和圆珠笔共15桶,所付金额超过570元,但不到580元.已知这两种笔的单价如图所示,设购买圆珠笔x桶,你能列出几个不等式?
应用
方案问题
感悟新知
1
某房地产开发公司计划建A、B两种户型的住房共80套.
该公司所筹资金不少于2090万元,但不超过2096万元,且所筹资金全部用于建房,两种户型的建房成本和售价如下表:
例 1
感悟新知
{5940675A-B579-460E-94D1-54222C63F5DA}
A型
B型
成本(万元/套)
25
28
售价(万元/套)
30
34
(1)该公司有哪几种建房方案?
(2)该公司如何建房可获得最大利润?
感悟新知
导引:本题中的不等关系为:建房资金不少于2090万元,不超过2096万元,可根据它们建立不等式组,即A型住房成本+B型住房成本22 090万元;A型住房成本+B型住房成本≤2 096万元.
感悟新知
解:(1)设建A型住房x套,则建B型住房(80-x)套.
根据题意,得
解得48≤x≤50.
因为x为整数,所以x=48,49,50.
所以有三种建房方案.
方案一:A型48套,B型32套;
方案二:A型49套,B型31套;
方案三:A型50套,B型30套.
感悟新知
(2)第一种方案获利:48 x(30-25)+32 x(34-28)=432(万元);第二种方案获利:49 x(30-25)+31 x(34-28)=431(万元);
第三种方案获利:50 x(30-25)+30 x(34-28)=430(万元).
所以选方案一获利最大.
总 结
感悟新知
求实际问题中方案的种类或最大值(最小值)问题时,常通过求不等式(组)的解集,分类讨论找出答案,即先根据题意设出未知数,列出不等式(组),求出相应的取值范围,再根据题目的条件分类讨论,写出答案.
1.某汽车租赁公司要购买轿车和面包车共10辆,其中轿车至少要购买3辆,轿车每辆7万元,面包车每辆4万元,公司可投入的购车款不超过55万元.
(1)符合公司要求的购车方案有哪几种?请说明理由;
(2)如果每辆轿车的日租金为200元,每辆面包车的日租金为110元,假设新购买的这10辆车每日都可租出,要使这10辆车的日租金收入不低于1 500元,那么应选择(1)中的哪种购车方案?
感悟新知
感悟新知
解析:设购买轿车x辆,由购买轿车和面包车共10辆,可知购买面包车(10-x)辆.购车款不超过55万元,即小于或等于55万元,所以可列不等式7x+4(10-x)≤55,考虑到实际情况,x只能取非负整数.
感悟新知
解:(1)设轿车要购买x辆,那么面包车要购买(10-x)辆.由题意,得7x+4(10-x)≤55,解得x≤5.因轿车至少要购买3辆,所以x≥3,且x为整数.所以x=3或x=4或x=5.所以购车方案有三种:方案一:轿车购买3辆,面包车购买7辆;方案二:轿车购买4辆,面包车购买6辆;方案三:轿车购买5辆,面包车购买5辆.
感悟新知
(2)方案一的日租金为3×200+7×110=1370(元);方案二的日租金为4×200+6×110=1460(元);方案三的日租金为5×200+5×110=1550(元).为保证日租金不低于1500元,应选择方案三.
感悟新知
例2
某学校为开展“阳光体育”活动,计划拿出不超过3000元的资金购买一批篮球、羽毛球拍和乒乓球拍,已知篮球、羽毛球拍和乒乓球拍的单价比为8:3:2,且其单价和为130元.
(1)请问篮球、羽毛球拍和乒乓球拍的单价分别是多少元?
(2)若要求购买篮球、羽毛球拍和乒乓球拍的总数量是80个(副),羽毛球拍的数量是篮球数量的4倍,且购买乒乓球拍的数量不超过15副,请问有几种购买方案?
感悟新知
导引:(1)已知篮球、羽毛球拍和乒乓球拍的单价比为8:3:2,且其单价和为130元,可以设它们的单价分别为8x元、3x元、2x元,列一元一次方程来解决问题;
(2)根据购买丘乓球拍的数量不超过15副和用不超过3 000元的资金购买一批篮球、羽毛球拍和乒乓球拍这两个不等关系列不等式组,求出购买篮球数量的范围,从而确定购买方案.
感悟新知
解:(1)因为篮球、羽毛球拍和乒乓球拍的单价比为8:3:2,所以,可设它们的单价分别为8x元、3x元、2x元,于是,得8x+3x+2x=130,解得x=10,所以,篮球、羽毛球拍和乒乓球拍的单价分别为80元、
30元和20元.
感悟新知
(2)设购买篮球的数量为y个,则购买羽毛球拍的数量为4y副,购买乒乓球拍的数量为(80-y-4y)副,根据题意,得
解不等式①.得y≤14.解不等式⑤,得y≥13.
于是,不等式组的解集为13≤y≤14.
感悟新知
因为y取整数,所以,只能取13或14.
因此,一共有两种购买方案:方案一:当y=13时,篮球购买13个,羽毛球拍购买52副,丘乓球拍购买15副;方案二:当y=14时,篮球购买14个,羽毛球拍购买56副,乒乓球拍购买10副.
感悟新知
总 结
解决这类问题的关键是在理解题意的基础上寻找明显或隐含的等量关系或不等关系,准确列出方程(组)或不等式(组).
课堂小结
利用不等式组解实际问题的关键是找出题目中所有的不等关系,列出不等式组,再解不等式组,最后根据实际情况确定合理的答案,解题时要注意两点:
(1)设未知数时,要将“不少于"不超过”等词语换成确定性词语.
(2)答案要满足两个条件:①符合题目要求:②符合实际情况
一元一次不等式组的应用
同课章节目录
