5.2.2导数的四则运算法则-2020-2021学年高二数学人教A版(2019)选择性必修第二册(15张PPT)
文档属性
| 名称 | 5.2.2导数的四则运算法则-2020-2021学年高二数学人教A版(2019)选择性必修第二册(15张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 117.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-02 09:22:19 | ||
图片预览






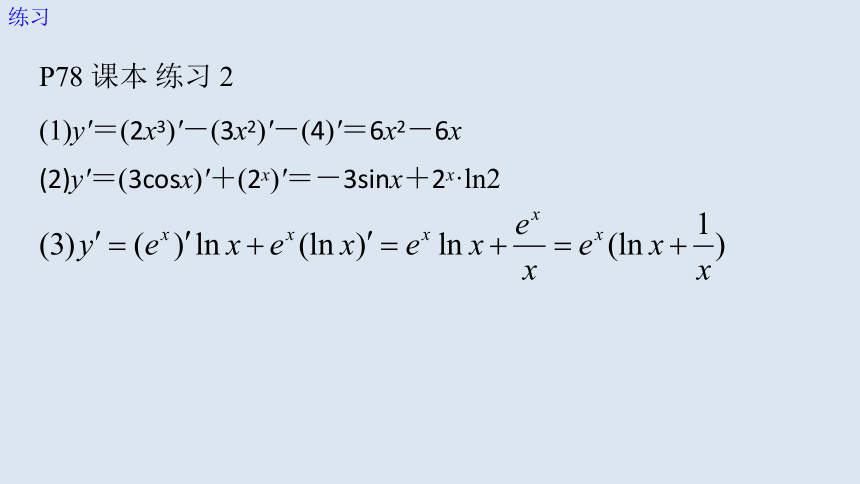
文档简介
(共15张PPT)
5.2.2
导数的四则运算法则
复习
基本初等函数的导数公式
1.若f(x)=c(c为常数)
,则f’(x)=c
2.若f(x)=xα(α∈Q且α≠0),则f’(x)=αxα-1
3.若f(x)=sinx
,则f’(x)=cosx
4.若f(x)=cosx
,则f’(x)=-sinx
5.若f(x)=ax
(a>0且a≠1),则f’(x)=axlna
特别地,若f(x)=ex
,则f’(x)=ex
6.若f(x)=logax
(a>0且a≠1),则
特别地,若f(x)=lnx
,则
探究
设f(x)=x2,g(x)=x,计算[f(x)+g(x)]'与[f(x)+g(x)]',它们f
'(x)与g'(x)和有什么关系?再取几组函数试试,由此你能想到什么?
解:设y=[f(x)+g(x)=x2+x,因为
所以[f(x)+g(x)]'=y'=
而f
'(x)=(x2)'=2x,g
'(x)=(x)'=1
所以[f(x)+g(x)]'=f
'(x)+g
'(x)
同样的,[f(x)-g(x)]'=f
'(x)-g
'(x)
新知
导数运算法则
1.[f(x)±g(x)]'=f
'(x)±g
'(x)
2.[f(x)·g(x)]'=f
'(x)g(x)+f(x)g
'(x)
特别的,[cf(x)]'=c
'f(x)+cf
'(x)=cf
'(x)
例题
例3.求下列函数的导数
(1)y=x3-x+3
(2)y=2x+cosx
解:(1)y'=(x3-x+3)'=(x3)'-(x)'+(3)'=3x2-1
(2)y'=(2x+cosx)'=(2x)'+(cosx)'=2xln2-sinx
例4.求下列函数的导数
(1)y=x3ex
(2)
解:(1)y'=(x3ex)'=(x3)'ex-x3(ex)'=3x2ex-x3ex
(1)利用函数的和、差、积、商的求导法则求函数的导数时,要分清函数的结构,再利用相应的法则进行求导.
(2)遇到函数的表达式是乘积形式或是商的形式,有时先将函数表达式展开或化简,然后再求导.
归纳
(1)y'=(2x3)'-(3x2)'-(4)'=6x2-6x
(2)y'=(3cosx)'+(2x)'=-3sinx+2x·ln2
P78
课本
练习
2
练习
P78
课本
练习
2
练习
练习
P78
课本
练习
2
若函数y=
(a>0)在x=x0处的导数为0,那么x0等于( )
A.a
B.±a
C.-a
D.a2
练习
若函数f(x)=exsinx,则此函数图象在点(4,f(4))处的切线的倾斜角为( )
A.直角
B.0
C.钝角
D.锐角
练习
例题
例5
日常生活中的饮用水通常是经过净化的,随着水的纯净度的提高,所需净化费用不断增加,已知将1t水净化到纯净度为x%所需费用(单位:元),为
(1)90%
(2)98%
解:净化费用的瞬时变化率就是净化费用函数的导数
(1)
所以,进化到纯净度为90%时,净化的瞬时变化率是52.84元/吨
例题
(2)
所以,进化到纯净度为98%时,净化的瞬时变化率是1321元/吨
函数f(x)在某点处导数的大小表示函数在此点附近变化的快慢。由上述计算可知,c'(98)=25c'(90).他表示进化到纯净度为98%左右时净化费用的变化率,大约是净化到纯净度为90%左右时净化费用变化率的25倍.这说明水的纯净度越高,需要的净化费用就越多,而且净化费用增加的速度也越快。
小结
导数运算法则
1.[f(x)±g(x)]'=f
'(x)±g
'(x)
2.[f(x)·g(x)]'=f
'(x)g(x)+f(x)g
'(x)
特别的,[cf(x)]'=c
'f(x)+cf
'(x)=cf
'(x)
作业
P78
课本
练习3
5.2.2
导数的四则运算法则
复习
基本初等函数的导数公式
1.若f(x)=c(c为常数)
,则f’(x)=c
2.若f(x)=xα(α∈Q且α≠0),则f’(x)=αxα-1
3.若f(x)=sinx
,则f’(x)=cosx
4.若f(x)=cosx
,则f’(x)=-sinx
5.若f(x)=ax
(a>0且a≠1),则f’(x)=axlna
特别地,若f(x)=ex
,则f’(x)=ex
6.若f(x)=logax
(a>0且a≠1),则
特别地,若f(x)=lnx
,则
探究
设f(x)=x2,g(x)=x,计算[f(x)+g(x)]'与[f(x)+g(x)]',它们f
'(x)与g'(x)和有什么关系?再取几组函数试试,由此你能想到什么?
解:设y=[f(x)+g(x)=x2+x,因为
所以[f(x)+g(x)]'=y'=
而f
'(x)=(x2)'=2x,g
'(x)=(x)'=1
所以[f(x)+g(x)]'=f
'(x)+g
'(x)
同样的,[f(x)-g(x)]'=f
'(x)-g
'(x)
新知
导数运算法则
1.[f(x)±g(x)]'=f
'(x)±g
'(x)
2.[f(x)·g(x)]'=f
'(x)g(x)+f(x)g
'(x)
特别的,[cf(x)]'=c
'f(x)+cf
'(x)=cf
'(x)
例题
例3.求下列函数的导数
(1)y=x3-x+3
(2)y=2x+cosx
解:(1)y'=(x3-x+3)'=(x3)'-(x)'+(3)'=3x2-1
(2)y'=(2x+cosx)'=(2x)'+(cosx)'=2xln2-sinx
例4.求下列函数的导数
(1)y=x3ex
(2)
解:(1)y'=(x3ex)'=(x3)'ex-x3(ex)'=3x2ex-x3ex
(1)利用函数的和、差、积、商的求导法则求函数的导数时,要分清函数的结构,再利用相应的法则进行求导.
(2)遇到函数的表达式是乘积形式或是商的形式,有时先将函数表达式展开或化简,然后再求导.
归纳
(1)y'=(2x3)'-(3x2)'-(4)'=6x2-6x
(2)y'=(3cosx)'+(2x)'=-3sinx+2x·ln2
P78
课本
练习
2
练习
P78
课本
练习
2
练习
练习
P78
课本
练习
2
若函数y=
(a>0)在x=x0处的导数为0,那么x0等于( )
A.a
B.±a
C.-a
D.a2
练习
若函数f(x)=exsinx,则此函数图象在点(4,f(4))处的切线的倾斜角为( )
A.直角
B.0
C.钝角
D.锐角
练习
例题
例5
日常生活中的饮用水通常是经过净化的,随着水的纯净度的提高,所需净化费用不断增加,已知将1t水净化到纯净度为x%所需费用(单位:元),为
(1)90%
(2)98%
解:净化费用的瞬时变化率就是净化费用函数的导数
(1)
所以,进化到纯净度为90%时,净化的瞬时变化率是52.84元/吨
例题
(2)
所以,进化到纯净度为98%时,净化的瞬时变化率是1321元/吨
函数f(x)在某点处导数的大小表示函数在此点附近变化的快慢。由上述计算可知,c'(98)=25c'(90).他表示进化到纯净度为98%左右时净化费用的变化率,大约是净化到纯净度为90%左右时净化费用变化率的25倍.这说明水的纯净度越高,需要的净化费用就越多,而且净化费用增加的速度也越快。
小结
导数运算法则
1.[f(x)±g(x)]'=f
'(x)±g
'(x)
2.[f(x)·g(x)]'=f
'(x)g(x)+f(x)g
'(x)
特别的,[cf(x)]'=c
'f(x)+cf
'(x)=cf
'(x)
作业
P78
课本
练习3
