【沪科版九年级数学上册课时作业】21.5.2 反比例函数的图象和性质(含答案)
文档属性
| 名称 | 【沪科版九年级数学上册课时作业】21.5.2 反比例函数的图象和性质(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 504.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-01 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
沪科版九年级数学上册课时作业
第21章 二次函数与反比例函数
21.5 反比例函数
第2课时 反比例函数的图象和性质
1. 已知点(-1,1)在反比例函数y=(k为常数,k≠0)的图象上,则这个反比例函数的大致图象 ( )
A B C D
2. 若反比例函数y=的图象在第一、三象限,则m的取值范围是 ( )
A. m≥1 B. m≤1 C. m<1 D. m>1
3. 如图,点A,B在反比例函数y=(k≠0,x>0)的图象上,过点A,B分别作x轴、y轴的垂线,则S1与S2的大小关系是 ( )
A. S1>S2 B. S1=S2 C. S14. 如图,在平面直角坐标系xOy中,函数y=kx+b(k≠0)与y=(m≠0)的图象相交于点A(2,3),B(-6,-1),则不等式kx+b>的解集为 ( )
A. x<-6 B. -62 C. x>2 D. x<-6或05. 若点A(-1,y1),B(1,y2),C(3,y3)在反比例函数y=-的图象上,则y1,y2,y3的大小关系是 ( )
A. y16. 已知点A是直线y=2x与双曲线y=(m为常数)一支的交点,过点A作x轴的垂线,垂足为B,且OB=2,则m的值为 ( )
A. -7 B. -8 C. 8 D. 7
7. 已知P1(x1,y1),P2(x2,y2)两点都在反比例函数y=的图象上,且x1“或“<“)?
8. 如图,A为反比例函数y=-图象上一点,过点A作AB⊥x轴于点B,连接OA,则△ABO的面积为 .?
9. 如图,点A,B分别在反比例函数y=和y=的图象上,且AB∥x轴,则△OAB的面积等于? .?
10. 如图,边长为4的正方形ABCD的对称中心是坐标原点O,AB∥x轴,BC∥y轴,反比例函数y=与y=-的图象均与正方形ABCD的边相交,则图中阴影部分的面积之和是 .?
11. 已知点A(a,b)是一次函数y=-x+4和反比例函数y=的一个交点,则代数式a2+b2的值为 .?
12. 已知点A(a,b)是一次函数y=-x+4和反比例函数y=-的一个交点,则代数式a-b的值为 .?
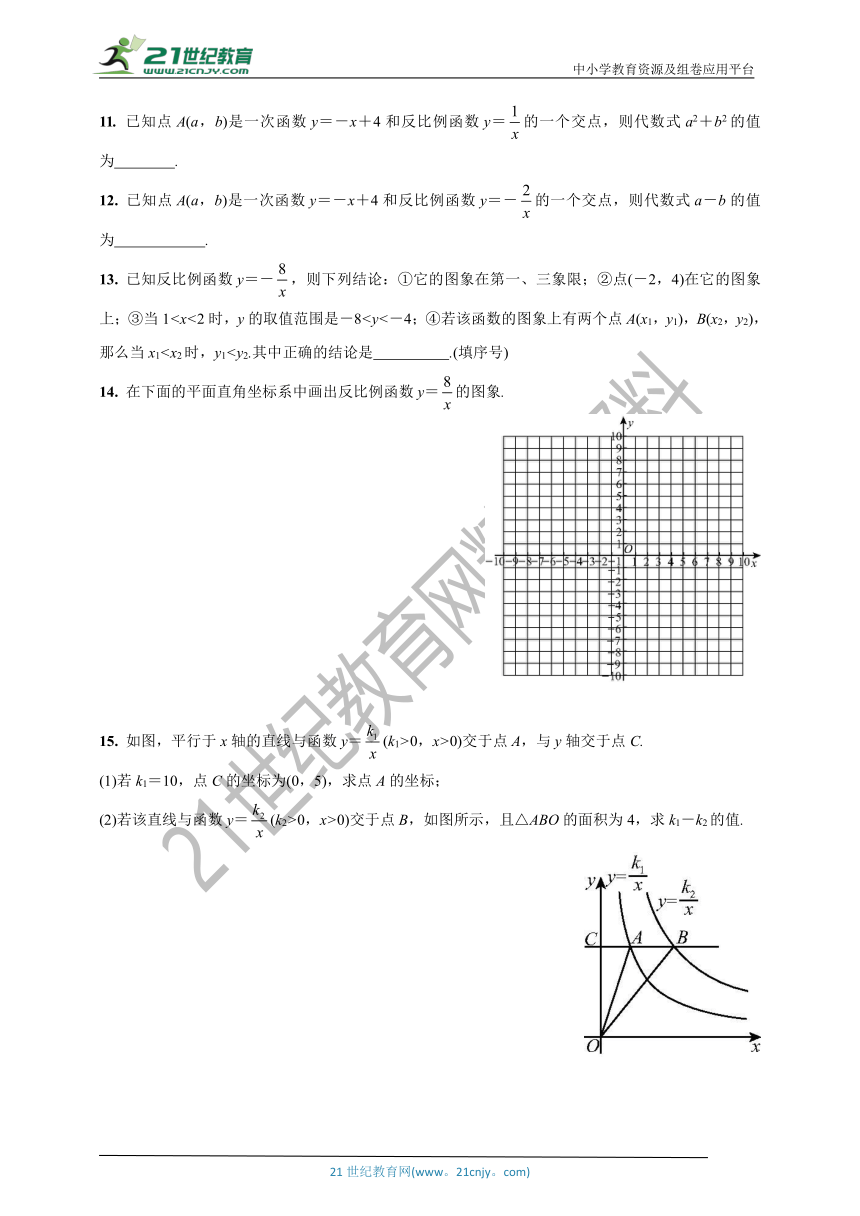
13. 已知反比例函数y=-,则下列结论:①它的图象在第一、三象限;②点(-2,4)在它的图象上;③当114. 在下面的平面直角坐标系中画出反比例函数y=的图象.
15. 如图,平行于x轴的直线与函数y=(k1>0,x>0)交于点A,与y轴交于点C.
(1)若k1=10,点C的坐标为(0,5),求点A的坐标;
(2)若该直线与函数y=(k2>0,x>0)交于点B,如图所示,且△ABO的面积为4,求k1-k2的值.
16. 已知A(-4,2),B(n,-4)两点是一次函数y=kx+b和反比例函数y=图象的两个交点.
(1)求一次函数和反比例函数的表达式;
(2)求△AOB的面积;
(3)观察图象,直接写出不等式kx+b->0的解集.
17. 如图,曲线C是函数y=在第一象限内的图象,抛物线是函数y=-x2-2x+4的图象,点Pn(x,y)(n=1,2,3,…)在曲线C上,且x,y都是整数.
(1)求出所有的点Pn(x,y);
(2)求抛物线y=-x2-2x+4的顶点坐标和对称轴;
(3)在Pn中任取两点作为点A和点B(点A的横坐标小于点B的横坐标),作直线AB,请直接写出能使直线AB与抛物线有交点的A,B的坐标,并求出直线AB的表达式.
参 考 答 案
1. D 2. D 3. B 4. B 5. B 6. D
7. >
8. 2
9.
10. 8
11. 14
12. ±2
13. ②③
14. 略
15. 解:(1)设点A的坐标为(a,b),∵AC∥x轴,点C的坐标为(0,5),∴b=5. 又∵点A在反比例函数y=的图象上,∴5a=10,∴a=2,∴点A的坐标为(2,5).
(2)由反比例函数中k的几何意义可得S△OAC=k1,S△OBC=k2. ∵S△ABO=S△OBC-S△OAC,∴4=(k2-k1),∴k2-k1=8,即k1-k2=-8.
16. 解:(1)反比例函数的表达式为y=-,一次函数的表达式为y=-x-2.
(2)令y=-x-2=0,则x=-2,所以OC=2. 所以S△AOB=S△AOC+S△BOC=×2×2+×2×4=6.
(3)由图象可知,不等式的解集为x<-4或017. 解:(1)∵y=,且x,y都是整数,∴或或或 ∴点P的坐标为(1,6),(2,3),(3,2),(6,1).
(2)∵y=-x2-2x+4=-(x+1)2+5,∴抛物线y=-x2-2x+4的顶点坐标为(-1,5),对称轴为直线x=-1.
(3)点A,B的坐标为(2,3),(6,1)或(3,2),(6,1). 设直线AB的表达式为y=kx+b,则有或 解得或 ∴直线AB的表达式为y=-x+4或y=-x+3.
_21?????????è?????(www???21cnjy???com)_
沪科版九年级数学上册课时作业
第21章 二次函数与反比例函数
21.5 反比例函数
第2课时 反比例函数的图象和性质
1. 已知点(-1,1)在反比例函数y=(k为常数,k≠0)的图象上,则这个反比例函数的大致图象 ( )
A B C D
2. 若反比例函数y=的图象在第一、三象限,则m的取值范围是 ( )
A. m≥1 B. m≤1 C. m<1 D. m>1
3. 如图,点A,B在反比例函数y=(k≠0,x>0)的图象上,过点A,B分别作x轴、y轴的垂线,则S1与S2的大小关系是 ( )
A. S1>S2 B. S1=S2 C. S1
A. x<-6 B. -6
A. y1
A. -7 B. -8 C. 8 D. 7
7. 已知P1(x1,y1),P2(x2,y2)两点都在反比例函数y=的图象上,且x1
8. 如图,A为反比例函数y=-图象上一点,过点A作AB⊥x轴于点B,连接OA,则△ABO的面积为 .?
9. 如图,点A,B分别在反比例函数y=和y=的图象上,且AB∥x轴,则△OAB的面积等于? .?
10. 如图,边长为4的正方形ABCD的对称中心是坐标原点O,AB∥x轴,BC∥y轴,反比例函数y=与y=-的图象均与正方形ABCD的边相交,则图中阴影部分的面积之和是 .?
11. 已知点A(a,b)是一次函数y=-x+4和反比例函数y=的一个交点,则代数式a2+b2的值为 .?
12. 已知点A(a,b)是一次函数y=-x+4和反比例函数y=-的一个交点,则代数式a-b的值为 .?
13. 已知反比例函数y=-,则下列结论:①它的图象在第一、三象限;②点(-2,4)在它的图象上;③当1
15. 如图,平行于x轴的直线与函数y=(k1>0,x>0)交于点A,与y轴交于点C.
(1)若k1=10,点C的坐标为(0,5),求点A的坐标;
(2)若该直线与函数y=(k2>0,x>0)交于点B,如图所示,且△ABO的面积为4,求k1-k2的值.
16. 已知A(-4,2),B(n,-4)两点是一次函数y=kx+b和反比例函数y=图象的两个交点.
(1)求一次函数和反比例函数的表达式;
(2)求△AOB的面积;
(3)观察图象,直接写出不等式kx+b->0的解集.
17. 如图,曲线C是函数y=在第一象限内的图象,抛物线是函数y=-x2-2x+4的图象,点Pn(x,y)(n=1,2,3,…)在曲线C上,且x,y都是整数.
(1)求出所有的点Pn(x,y);
(2)求抛物线y=-x2-2x+4的顶点坐标和对称轴;
(3)在Pn中任取两点作为点A和点B(点A的横坐标小于点B的横坐标),作直线AB,请直接写出能使直线AB与抛物线有交点的A,B的坐标,并求出直线AB的表达式.
参 考 答 案
1. D 2. D 3. B 4. B 5. B 6. D
7. >
8. 2
9.
10. 8
11. 14
12. ±2
13. ②③
14. 略
15. 解:(1)设点A的坐标为(a,b),∵AC∥x轴,点C的坐标为(0,5),∴b=5. 又∵点A在反比例函数y=的图象上,∴5a=10,∴a=2,∴点A的坐标为(2,5).
(2)由反比例函数中k的几何意义可得S△OAC=k1,S△OBC=k2. ∵S△ABO=S△OBC-S△OAC,∴4=(k2-k1),∴k2-k1=8,即k1-k2=-8.
16. 解:(1)反比例函数的表达式为y=-,一次函数的表达式为y=-x-2.
(2)令y=-x-2=0,则x=-2,所以OC=2. 所以S△AOB=S△AOC+S△BOC=×2×2+×2×4=6.
(3)由图象可知,不等式的解集为x<-4或0
(2)∵y=-x2-2x+4=-(x+1)2+5,∴抛物线y=-x2-2x+4的顶点坐标为(-1,5),对称轴为直线x=-1.
(3)点A,B的坐标为(2,3),(6,1)或(3,2),(6,1). 设直线AB的表达式为y=kx+b,则有或 解得或 ∴直线AB的表达式为y=-x+4或y=-x+3.
_21?????????è?????(www???21cnjy???com)_
