11.1杠杆 计算 2021-2022学年苏科版九年级物理 上学期 (含答案)
文档属性
| 名称 | 11.1杠杆 计算 2021-2022学年苏科版九年级物理 上学期 (含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 229.1KB | ||
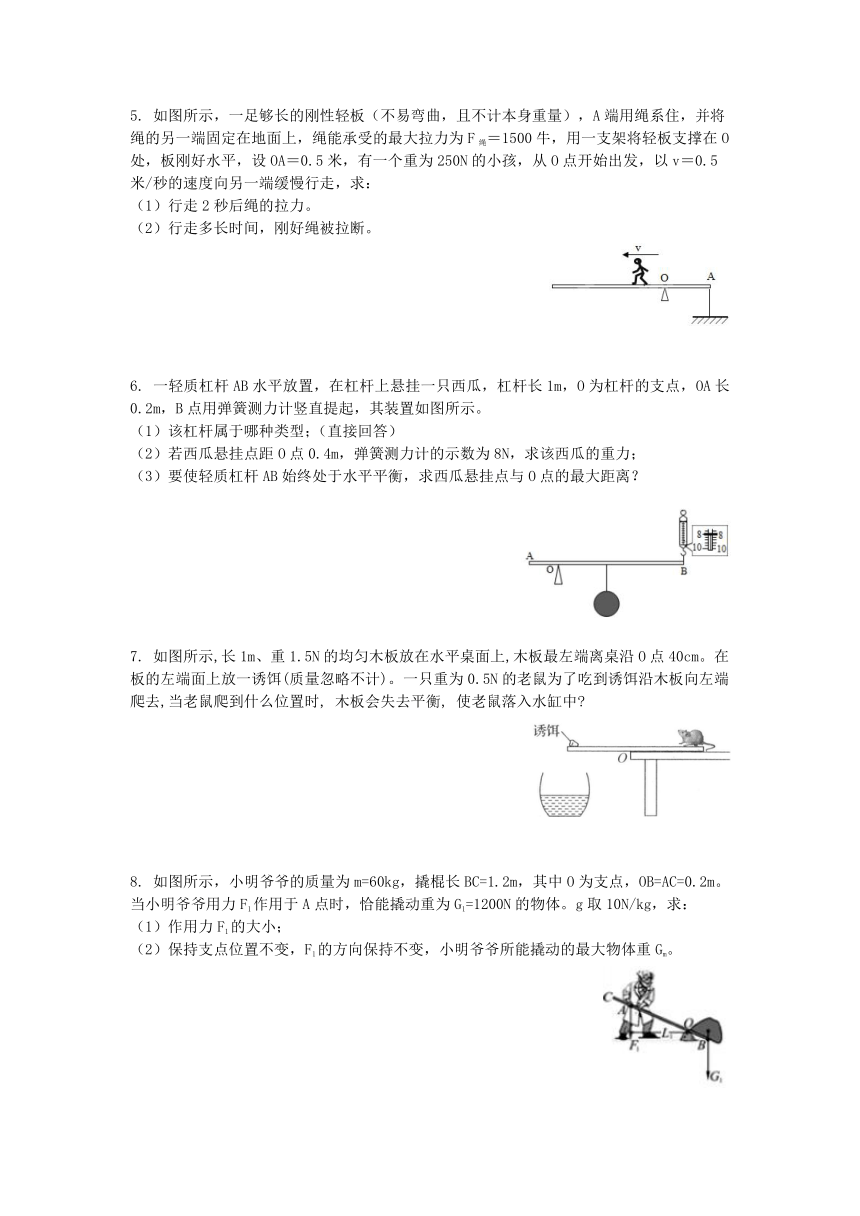
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-08-01 14:55:31 | ||
图片预览


文档简介
第十一章 简单机械和功 第一节杠杆 本节突破之计算
计算题
1.如图所示,小华正在做俯卧撑,可以将他的身体看成一个杠杆,O为支点,A为他的重心,相关长度已在图中标明,已知他的质量m=60kg。求:
(1)小华受到的重力G;
(2)图示时刻地面对双手支持力F的力臂L1和阻力臂L2;
(3)图示时刻地面对双手的支持力F。
2. 如图所示,将质量为6kg,边长为0.1m的正方体合金块,用细线挂在轻质杠杆A点处,在B点施加与杠杆垂直的力F1时,杠杆在水平位置平衡,其中OB=3OA(g取10N/kg)求:
(1)合金块的重力;
(2)合金块的密度;
(3)拉力F1的大小。
3. 如图所示,一轻质杠杆OA可绕O点无摩擦转动,A端用绳子系在竖直墙壁的B点,在杠杆的C点悬挂一重为30 N的物体,杠杆处于水平静止状态.已知OA长为50 cm,OC长为30 cm,∠OAB=30°.
(1)请在图中画出绳子对杠杆拉力F的力臂L1.
(2)拉力F的大小是多少?
4. 已知一根质量分布均匀的圆柱体木料质量为60kg,体积为0.1m3。问:
(1)此木料的密度为多少?
(2)如图所示,甲、乙两人分别在A点和B点共同扛起此木料并恰好水平,其中AO=BO,O为木料的中点。求此时乙对木料的作用力大小。
(3)若在(2)中当乙的作用点从B点向O点靠近时,请列式分析此过程中甲对木料作用力大小变化情况。
5. 如图所示,一足够长的刚性轻板(不易弯曲,且不计本身重量),A端用绳系住,并将绳的另一端固定在地面上,绳能承受的最大拉力为F绳=1500牛,用一支架将轻板支撑在O处,板刚好水平,设OA=0.5米,有一个重为250N的小孩,从O点开始出发,以v=0.5米/秒的速度向另一端缓慢行走,求:
(1)行走2秒后绳的拉力。
(2)行走多长时间,刚好绳被拉断。
6. 一轻质杠杆AB水平放置,在杠杆上悬挂一只西瓜,杠杆长1m,O为杠杆的支点,OA长0.2m,B点用弹簧测力计竖直提起,其装置如图所示。
(1)该杠杆属于哪种类型;(直接回答)
(2)若西瓜悬挂点距O点0.4m,弹簧测力计的示数为8N,求该西瓜的重力;
(3)要使轻质杠杆AB始终处于水平平衡,求西瓜悬挂点与O点的最大距离?
7. 如图所示,长1m、重1.5N的均匀木板放在水平桌面上,木板最左端离桌沿O点40cm。在板的左端面上放一诱饵(质量忽略不计)。一只重为0.5N的老鼠为了吃到诱饵沿木板向左端爬去,当老鼠爬到什么位置时, 木板会失去平衡, 使老鼠落入水缸中?
8. 如图所示,小明爷爷的质量为m=60kg,撬棍长BC=1.2m,其中O为支点,OB=AC=0.2m。当小明爷爷用力F1作用于A点时,恰能撬动重为G1=1200N的物体。g取10N/kg,求:
(1)作用力F1的大小;
(2)保持支点位置不变,F1的方向保持不变,小明爷爷所能撬动的最大物体重Gm。
9. 农家乐活动,大明用一根扁担(轻质竹棒)挑起质量为6kg的物体,扁担保持水平状态,AB=0.6m、BC=1.2m.g取10Nkg,求:
(1)大明的手对扁担的拉力大小是多少N?
(2)大明肩膀对扁担支持力的大小?
10. 如图所示,质量不计的光滑木板AB长1.6m,可绕固定点O转动,离O点0.4m的B端挂一重物G,板的A端用一根与水平地面成30°夹角的细绳拉住,木板在水平位置平衡时绳的拉力是8N.然后在O点的正上方放一质量为0.5kg的小球,若小球以20cm/s的速度由O点沿木板向A端匀速运动,问小球至少运动多长时间细绳的拉力减小到零.(取g=10N/kg,绳的重力不计)
11. 如图所示,独轮车和车内的煤的总质量为100kg,其重力可视为作用于A点.车轴O为支点,取
这独轮车使用时是省力杠杆还是费力杠杆?请说出判断理由
独轮车和车内的煤的总重力为多少?? ? ? ?
将车把抬起时,作用在车把向上的力为多少?
答案
1.解:(1)小华受到的重力:G=mg=60kg×10N/kg=600N;
(2)由图可知,动力臂L1=100cm+50cm=150cm,阻力臂L2=100cm;
(3)根据杠杆平衡的条件可得:
FL1=GL2,
F×150cm=600N×100cm,
解得:F=400N。
答:(1)小华受到的重力为600N;
(2)图示时刻地面对双手支持力F的力臂L1和阻力臂L2分别为150cm和100cm;
(3)图示时刻地面对双手的支持力为400N。
2. (1)合金块的重力:
G=mg=6kg×10N/kg=60N;
(2)正方体合金块的体积:
V=L3=(0.1m)3=10-3m3;
合金块的密度:
==6×103kg/m3;
(3)已知OB=3OA,F2=G=60N,
根据杠杆的平衡条件可得:F1LOB=F2LOA,
则拉力F1的大小:F1===×60N=20N。
答:(1)合金块的重力为60N;
(2)合金块的密度为6×103kg/m3;
(3)拉力F1的大小为20N。
3. 解:(1)过支点O作垂直绳子对杠杆的拉力F作用线的垂线段(即力臂L1)。
如图所示:
(2)如上图所示,在Rt△OAD中,∠ODA=90°,∠DAO=30°,
∴
根据杠杆平衡条件得:F×OD=G×OC
即F×25cm=30N×30cm
解得:F=36N
答:拉力F的大小为36N。
4. 解:(1)由题知木料质量为60kg,体积为0.1m3,带入密度公式得:;
(2)木料重力G=mg=60kg×10N/kg=600N;
以A为支点,可以将质量分布均匀的木料所受的重力等效于其重心O点,则;
则由杠杆平衡条件F1l1=F2l2得:F乙×AB=G×AO;
即;
(3)当乙的作用点向O靠近时,此时作用点记为B′;
以A为支点,由杠杆平衡条件F1l1=F2l2得:F乙×AB′=G×AO;
即;
当乙向O点靠近,AB′减小,G与AO不变,则F乙变大;
因为木料处于平衡状态,故所受合力为零,则有F乙+F甲=G;
因F乙变大,所以F甲变小。
答:(1)木料密度为600kg/m3;
(2)此时乙对木料的作用力F乙=300N;
(3)当乙的作用点从B点向O点靠近时,F甲变小。
5.解:
(1)行走2s?后,小孩行走的距离为:L1=s=vt=0.5m/s×2s=1m,
因为F1L1=F2L2,所以,250N×1m=F2×0.5m,所以,F2=500N;
(2)绳刚好被拉断时,绳子A端的拉力为F绳=1500N,
因为F1L'1= F绳L2,所以,250N×L'1=1500N×0.5m,所以,L'1=3m,
所以小孩行走的时间为:t'==6s。
答:
(1)行走2s?后绳的拉力为500N;
(2)行走6s,刚好绳被拉断。
6. 解:(1)O为杠杆的支点,B点用弹簧测力计竖直提起,根据力臂的定义,OB为动力臂,西瓜悬挂点距O点的距离为阻力臂,因动力臂大于阻力臂,故该杠杆属于省力杠杆;
(2)杠杆长1m,O为杠杆的支点,OA长0.2m,L1=OB=1m-0.2m=0.8m,阻力臂:L2=0.4m,西瓜的重力为阻力,由杠杆平衡条件可得,
G×L2=F×L1,
西瓜的重力:
G=×F=×8N=16N;
(2)由图知,弹簧测力计的量程为0~10N,
当弹簧测力计的示数为10N时,根据杠杆平衡条件知,G×d''=F最大×(AB-OA),
则,16N×d''=10N×(1m-0.2m),
解得,西瓜悬挂点与O点的最大距离d''=0.5m。
答:(1)该杠杆属于省力杠杆;
(2)该西瓜的重力为16N;
(3)西瓜悬挂点与O点的最大距离为0.5m。
7. 设木板的重心在A处,当老鼠爬到B处时杠杆刚好能够平衡,如图所示:
;
则老鼠的力臂为OB,木板重力的力臂为OA,OA=×1m-0.4m=0.1m,根据杠杆的平衡条件得:
G鼠OB=G板OA,代入数据得:
0.5N×OB=1.5N×0.1m
则:OB=0.3m
答:当老鼠爬到O点左端0.3m处木板会失去平衡,使老鼠落入水桶中.
8. 解:
(1)因为OB=AC=0.2m,BC=1.2m,
AB=BC-AC=1.2m-0.2m=1m,
OA=AB-OB=1m-0.2m=0.8m,
由三角形相似得===,
由杠杆的平衡条件得,F1L1=G1L2,
==,
F1=G1==300N;
(2)支点位置不动,F1的方向保持不变,小明爷爷要想撬动最大物重,应使动力臂最长,
因为最大动力为小明爷爷重力F1=G=mg=60kg×10N/kg=600N,
由三角形相似得,====,
根据杠杆的平衡条件F1L1=GmL2得,
==;
=,
解得最大物重:
Gm=3000N。
答:(1)作用力F1的大小为300N;
(2)保持支点位置不变,小明爷爷所能撬动的最大物体重Gm=3000N。
9. 解:(1)以B为支点,根据杠杆的平衡条件可得:F×AB=G×BC,
即:F×0.6m=60N×1.2m,
解得大明的手对扁担的拉力:F=120N;
(2)①物体的重力:
G=mg=6kg×10N/kg=60N;
以A为支点,根据杠杆的平衡条件可得:F'×AB=G×AC,
即:F'×0.6m=60N×1.8m,
解得肩膀对扁担支持力:F'=180N。
②对扁担受力分析知:扁担受重物的拉力F拉、手向下的压力F、肩膀向上的支持力F支,
重物对扁担的拉力等于重物的重力,即F拉=G=60N,
肩膀对扁担的支持力:F支=F+G=120N+60N=180N。
答:(1)大明的手对扁担的拉力大小为120N;
(2)大明肩膀对扁担支持力的大小为180N。
10. 解:做出拉力的力臂,如图所示:
根据杠杆平衡条件得:F绳×AO=G×BO
即:8N××(1.6m-0.4m)=G×0.4m
∴G=12N
(2)球的重力G球=m球g=0.5kg×10N/kg=5N
当绳子拉力为0时,设球离O点距离为L球,则根据杠杆平衡条件得:
G球×L球=G×BO
即:5N×L球=12N×0.4m,
∴L球=0.96m=96cm
运动时间t===4.8s。
答:小球运动4.8s时绳子拉力为零。
11. (1)由图可知:F1是动力,F2是阻力,O是支点.动力臂L1=70cm+30cm=100cm,阻力臂L2=30cm,
则动力臂大于阻力臂,所以使用该车时是省力杠杆.
(2)独轮车和车内煤的总重力:G=mg=100kg×10N/kg=1000N;
(3)根据杠杆平衡条件:F1L1=F2L2得F1×100cm=1000N×30cm,所以F1=300N.
答:(1)这独轮车使用时是省力杠杆;(2)独轮车和车内的煤的总重力为1000N;(3)将车把抬起时,作用在车把向上的力为300N。
计算题
1.如图所示,小华正在做俯卧撑,可以将他的身体看成一个杠杆,O为支点,A为他的重心,相关长度已在图中标明,已知他的质量m=60kg。求:
(1)小华受到的重力G;
(2)图示时刻地面对双手支持力F的力臂L1和阻力臂L2;
(3)图示时刻地面对双手的支持力F。
2. 如图所示,将质量为6kg,边长为0.1m的正方体合金块,用细线挂在轻质杠杆A点处,在B点施加与杠杆垂直的力F1时,杠杆在水平位置平衡,其中OB=3OA(g取10N/kg)求:
(1)合金块的重力;
(2)合金块的密度;
(3)拉力F1的大小。
3. 如图所示,一轻质杠杆OA可绕O点无摩擦转动,A端用绳子系在竖直墙壁的B点,在杠杆的C点悬挂一重为30 N的物体,杠杆处于水平静止状态.已知OA长为50 cm,OC长为30 cm,∠OAB=30°.
(1)请在图中画出绳子对杠杆拉力F的力臂L1.
(2)拉力F的大小是多少?
4. 已知一根质量分布均匀的圆柱体木料质量为60kg,体积为0.1m3。问:
(1)此木料的密度为多少?
(2)如图所示,甲、乙两人分别在A点和B点共同扛起此木料并恰好水平,其中AO=BO,O为木料的中点。求此时乙对木料的作用力大小。
(3)若在(2)中当乙的作用点从B点向O点靠近时,请列式分析此过程中甲对木料作用力大小变化情况。
5. 如图所示,一足够长的刚性轻板(不易弯曲,且不计本身重量),A端用绳系住,并将绳的另一端固定在地面上,绳能承受的最大拉力为F绳=1500牛,用一支架将轻板支撑在O处,板刚好水平,设OA=0.5米,有一个重为250N的小孩,从O点开始出发,以v=0.5米/秒的速度向另一端缓慢行走,求:
(1)行走2秒后绳的拉力。
(2)行走多长时间,刚好绳被拉断。
6. 一轻质杠杆AB水平放置,在杠杆上悬挂一只西瓜,杠杆长1m,O为杠杆的支点,OA长0.2m,B点用弹簧测力计竖直提起,其装置如图所示。
(1)该杠杆属于哪种类型;(直接回答)
(2)若西瓜悬挂点距O点0.4m,弹簧测力计的示数为8N,求该西瓜的重力;
(3)要使轻质杠杆AB始终处于水平平衡,求西瓜悬挂点与O点的最大距离?
7. 如图所示,长1m、重1.5N的均匀木板放在水平桌面上,木板最左端离桌沿O点40cm。在板的左端面上放一诱饵(质量忽略不计)。一只重为0.5N的老鼠为了吃到诱饵沿木板向左端爬去,当老鼠爬到什么位置时, 木板会失去平衡, 使老鼠落入水缸中?
8. 如图所示,小明爷爷的质量为m=60kg,撬棍长BC=1.2m,其中O为支点,OB=AC=0.2m。当小明爷爷用力F1作用于A点时,恰能撬动重为G1=1200N的物体。g取10N/kg,求:
(1)作用力F1的大小;
(2)保持支点位置不变,F1的方向保持不变,小明爷爷所能撬动的最大物体重Gm。
9. 农家乐活动,大明用一根扁担(轻质竹棒)挑起质量为6kg的物体,扁担保持水平状态,AB=0.6m、BC=1.2m.g取10Nkg,求:
(1)大明的手对扁担的拉力大小是多少N?
(2)大明肩膀对扁担支持力的大小?
10. 如图所示,质量不计的光滑木板AB长1.6m,可绕固定点O转动,离O点0.4m的B端挂一重物G,板的A端用一根与水平地面成30°夹角的细绳拉住,木板在水平位置平衡时绳的拉力是8N.然后在O点的正上方放一质量为0.5kg的小球,若小球以20cm/s的速度由O点沿木板向A端匀速运动,问小球至少运动多长时间细绳的拉力减小到零.(取g=10N/kg,绳的重力不计)
11. 如图所示,独轮车和车内的煤的总质量为100kg,其重力可视为作用于A点.车轴O为支点,取
这独轮车使用时是省力杠杆还是费力杠杆?请说出判断理由
独轮车和车内的煤的总重力为多少?? ? ? ?
将车把抬起时,作用在车把向上的力为多少?
答案
1.解:(1)小华受到的重力:G=mg=60kg×10N/kg=600N;
(2)由图可知,动力臂L1=100cm+50cm=150cm,阻力臂L2=100cm;
(3)根据杠杆平衡的条件可得:
FL1=GL2,
F×150cm=600N×100cm,
解得:F=400N。
答:(1)小华受到的重力为600N;
(2)图示时刻地面对双手支持力F的力臂L1和阻力臂L2分别为150cm和100cm;
(3)图示时刻地面对双手的支持力为400N。
2. (1)合金块的重力:
G=mg=6kg×10N/kg=60N;
(2)正方体合金块的体积:
V=L3=(0.1m)3=10-3m3;
合金块的密度:
==6×103kg/m3;
(3)已知OB=3OA,F2=G=60N,
根据杠杆的平衡条件可得:F1LOB=F2LOA,
则拉力F1的大小:F1===×60N=20N。
答:(1)合金块的重力为60N;
(2)合金块的密度为6×103kg/m3;
(3)拉力F1的大小为20N。
3. 解:(1)过支点O作垂直绳子对杠杆的拉力F作用线的垂线段(即力臂L1)。
如图所示:
(2)如上图所示,在Rt△OAD中,∠ODA=90°,∠DAO=30°,
∴
根据杠杆平衡条件得:F×OD=G×OC
即F×25cm=30N×30cm
解得:F=36N
答:拉力F的大小为36N。
4. 解:(1)由题知木料质量为60kg,体积为0.1m3,带入密度公式得:;
(2)木料重力G=mg=60kg×10N/kg=600N;
以A为支点,可以将质量分布均匀的木料所受的重力等效于其重心O点,则;
则由杠杆平衡条件F1l1=F2l2得:F乙×AB=G×AO;
即;
(3)当乙的作用点向O靠近时,此时作用点记为B′;
以A为支点,由杠杆平衡条件F1l1=F2l2得:F乙×AB′=G×AO;
即;
当乙向O点靠近,AB′减小,G与AO不变,则F乙变大;
因为木料处于平衡状态,故所受合力为零,则有F乙+F甲=G;
因F乙变大,所以F甲变小。
答:(1)木料密度为600kg/m3;
(2)此时乙对木料的作用力F乙=300N;
(3)当乙的作用点从B点向O点靠近时,F甲变小。
5.解:
(1)行走2s?后,小孩行走的距离为:L1=s=vt=0.5m/s×2s=1m,
因为F1L1=F2L2,所以,250N×1m=F2×0.5m,所以,F2=500N;
(2)绳刚好被拉断时,绳子A端的拉力为F绳=1500N,
因为F1L'1= F绳L2,所以,250N×L'1=1500N×0.5m,所以,L'1=3m,
所以小孩行走的时间为:t'==6s。
答:
(1)行走2s?后绳的拉力为500N;
(2)行走6s,刚好绳被拉断。
6. 解:(1)O为杠杆的支点,B点用弹簧测力计竖直提起,根据力臂的定义,OB为动力臂,西瓜悬挂点距O点的距离为阻力臂,因动力臂大于阻力臂,故该杠杆属于省力杠杆;
(2)杠杆长1m,O为杠杆的支点,OA长0.2m,L1=OB=1m-0.2m=0.8m,阻力臂:L2=0.4m,西瓜的重力为阻力,由杠杆平衡条件可得,
G×L2=F×L1,
西瓜的重力:
G=×F=×8N=16N;
(2)由图知,弹簧测力计的量程为0~10N,
当弹簧测力计的示数为10N时,根据杠杆平衡条件知,G×d''=F最大×(AB-OA),
则,16N×d''=10N×(1m-0.2m),
解得,西瓜悬挂点与O点的最大距离d''=0.5m。
答:(1)该杠杆属于省力杠杆;
(2)该西瓜的重力为16N;
(3)西瓜悬挂点与O点的最大距离为0.5m。
7. 设木板的重心在A处,当老鼠爬到B处时杠杆刚好能够平衡,如图所示:
;
则老鼠的力臂为OB,木板重力的力臂为OA,OA=×1m-0.4m=0.1m,根据杠杆的平衡条件得:
G鼠OB=G板OA,代入数据得:
0.5N×OB=1.5N×0.1m
则:OB=0.3m
答:当老鼠爬到O点左端0.3m处木板会失去平衡,使老鼠落入水桶中.
8. 解:
(1)因为OB=AC=0.2m,BC=1.2m,
AB=BC-AC=1.2m-0.2m=1m,
OA=AB-OB=1m-0.2m=0.8m,
由三角形相似得===,
由杠杆的平衡条件得,F1L1=G1L2,
==,
F1=G1==300N;
(2)支点位置不动,F1的方向保持不变,小明爷爷要想撬动最大物重,应使动力臂最长,
因为最大动力为小明爷爷重力F1=G=mg=60kg×10N/kg=600N,
由三角形相似得,====,
根据杠杆的平衡条件F1L1=GmL2得,
==;
=,
解得最大物重:
Gm=3000N。
答:(1)作用力F1的大小为300N;
(2)保持支点位置不变,小明爷爷所能撬动的最大物体重Gm=3000N。
9. 解:(1)以B为支点,根据杠杆的平衡条件可得:F×AB=G×BC,
即:F×0.6m=60N×1.2m,
解得大明的手对扁担的拉力:F=120N;
(2)①物体的重力:
G=mg=6kg×10N/kg=60N;
以A为支点,根据杠杆的平衡条件可得:F'×AB=G×AC,
即:F'×0.6m=60N×1.8m,
解得肩膀对扁担支持力:F'=180N。
②对扁担受力分析知:扁担受重物的拉力F拉、手向下的压力F、肩膀向上的支持力F支,
重物对扁担的拉力等于重物的重力,即F拉=G=60N,
肩膀对扁担的支持力:F支=F+G=120N+60N=180N。
答:(1)大明的手对扁担的拉力大小为120N;
(2)大明肩膀对扁担支持力的大小为180N。
10. 解:做出拉力的力臂,如图所示:
根据杠杆平衡条件得:F绳×AO=G×BO
即:8N××(1.6m-0.4m)=G×0.4m
∴G=12N
(2)球的重力G球=m球g=0.5kg×10N/kg=5N
当绳子拉力为0时,设球离O点距离为L球,则根据杠杆平衡条件得:
G球×L球=G×BO
即:5N×L球=12N×0.4m,
∴L球=0.96m=96cm
运动时间t===4.8s。
答:小球运动4.8s时绳子拉力为零。
11. (1)由图可知:F1是动力,F2是阻力,O是支点.动力臂L1=70cm+30cm=100cm,阻力臂L2=30cm,
则动力臂大于阻力臂,所以使用该车时是省力杠杆.
(2)独轮车和车内煤的总重力:G=mg=100kg×10N/kg=1000N;
(3)根据杠杆平衡条件:F1L1=F2L2得F1×100cm=1000N×30cm,所以F1=300N.
答:(1)这独轮车使用时是省力杠杆;(2)独轮车和车内的煤的总重力为1000N;(3)将车把抬起时,作用在车把向上的力为300N。
同课章节目录
- 第十一章 简单机械和功
- 1 杠杆
- 2 滑轮
- 3 功
- 4 功率
- 5 机械效率
- 第十二章 机械能和内能
- 1 动能 势能 机械能
- 2 内能 热传递
- 3 物质的比热容
- 4 机械能和内能的相互转化
- 第十三章 电路初探
- 1 初识家用电器和电路
- 2 电路连接的基本方式
- 3 电流和电流表的使用
- 4 电压和电压表的使用
- 第十四章 欧姆定律
- 1 电阻
- 2 变阻器
- 3 欧姆定律
- 4 欧姆定律的应用
- 第十五章 电功和电热
- 电能表与电功
- 电功率
- 电热器 电流的热效应
- 家庭电路与安全用电
- 第十六章 电磁转换
- 磁体与磁场
- 电流的磁场
- 磁场对电流的作用 电动机
- 安装直流电动机模型
- 电磁感应 发电机
- 第十七章 电磁波与现代通信
- 信息与信息传播
- 电磁波及其传播
- 现代通信 走进信息时代
- 第十八章 能源与可持续发展
- 能源利用与社会发展
- 核能
- 太阳能
- 能量转化的基本规律
- 能源与可持续发展
