2021-2022学年高中信息技术粤教版(2019)必修1 数据与计算 3.2 算法及其描述 教学课件 (共18张PPT)
文档属性
| 名称 | 2021-2022学年高中信息技术粤教版(2019)必修1 数据与计算 3.2 算法及其描述 教学课件 (共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 粤教版(2019) | ||
| 科目 | 信息技术(信息科技) | ||
| 更新时间 | 2021-08-01 00:00:00 | ||
图片预览





文档简介
(共18张PPT)
3 . 2 算 法 及 其 描 述
初识算法
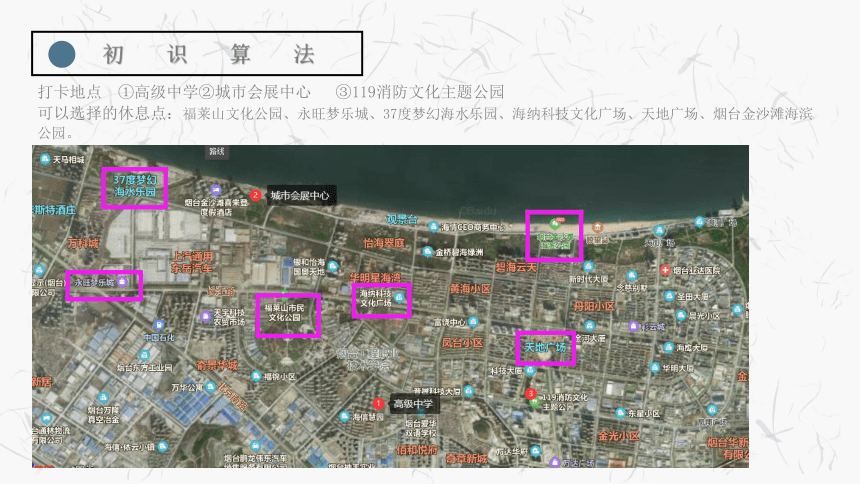
为了庆祝建党一百周年,高级中学举办了“百年逐梦路,青春励志行”研学旅行活动。相信同学们参加后受到了很大的鼓舞,从深层次的感悟到了红色历史、红色文化,也加深了与同学们之间的友谊。我们兄弟学校的李明同学也迫不及待的想要组织一次远足活动,请同学们根据地图上标识的打卡地点,在每个打卡地点中安排一到两个休息点,帮助李明同学设计一条的远足路线。
初识算法
打卡地点 ①高级中学②城市会展中心 ③119消防文化主题公园
可以选择的休息点:福莱山文化公园、永旺梦乐城、37度梦幻海水乐园、海纳科技文化广场、天地广场、烟台金沙滩海滨公园。
算法定义
算法,就是在有限步骤内,求解某一问题所使用的一组定义明确的规则。
示例:判断6x +9x+7=0是否有实数根。
①计算d=9*9-4*6*7
②判断d是否大于等于0,如果是执行步骤③,否则执行步骤④
③输出此方程有实数根
④输出此方程无实数根
算法定义
任务1 设计算法:输入a、b两个数的值,输出时交换两个数的值。
①输入a和b
②另取一个值c,把a的值赋给c
③将b的值赋给a
④将c的值赋给b
⑤输出a,b
算法特征
分析算法 判断6x +9x+7=0是否有实数根 输入a、b两个数的值,输出时交换两个数的值
是否有输入?
是否有输出?
执行的步骤个数是多少?
每一步是否有确切的含义?
是否能在有限的时间完成?
任务2 根据示例和任务1的算法,填写以下分析算法的表格
算法特征
算
法
的
特
征
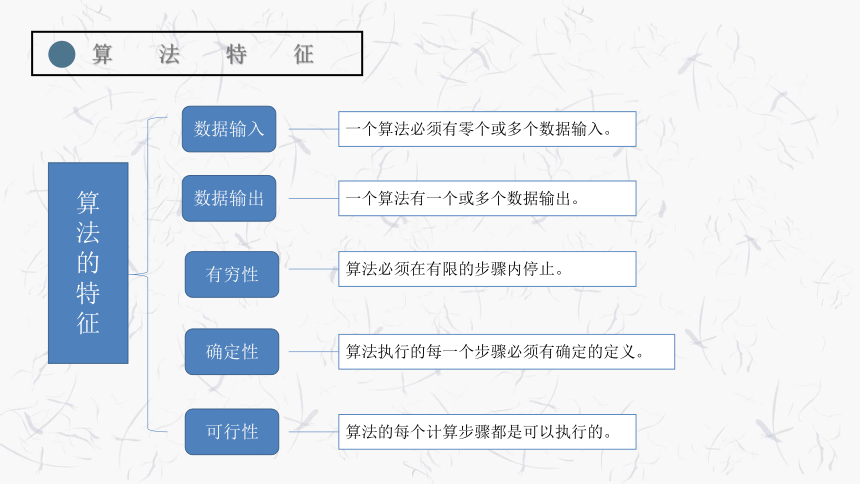
数据输入
一个算法必须有零个或多个数据输入。
数据输出
一个算法有一个或多个数据输出。
有穷性
算法必须在有限的步骤内停止。
确定性
算法执行的每一个步骤必须有确定的定义。
可行性
算法的每个计算步骤都是可以执行的。
算法描述
实践1:李明同学想用一款软件测量他们走了多远,他平时运动时喜欢用爱动APP去测量步数,可以奖励积分,积分可以用来兑换名著。该APP规定,每走1000步就奖励2个积分,请同学们设计算法,实现输入相应的步数t就能看到有多少积分d。
算法描述
1、自然语言:人们日常所用的语言。
易于理解
引起歧义
①输入步数t
②计算积分d=t/1000*2
③输出积分d
他原来在这里
(1)以前
(2)表示某种真实的情况
算法描述
2、伪代码:介于自然语言和计算机语言之间的文字和符号。
格式紧凑、书写方便、便于向计算机程序设计语言过渡
不适用于没有代码基础的初学者
Input t
d=t/1000*2
Print d
算法描述
3、流程图:步骤简洁清晰、算法结构表达明确、直观易读。
图形 名称 功能
开始/结束 表示算法的开始或结束
输入/输出 表示算法中变量的输入或输出
处理 表示算法中变量的计算与赋值
判断 表示算法中的条件判断
流程线 表示算法中的流向
连接点 表示算法中的转接
算法描述
①输入步数t
②计算积分d=t/1000*2
③输出积分d
开始
输入t
d=t/1000*2
输出d
结束
请同学们对应着自然语言,自主学习流程图图形(课本P50),将此流程图补充完整。
开始
输入t
d=t/1000*2
输出d
结束
算法描述
实践2:后期爱动APP对奖励规则进行了更新,每天走路的前4000步,每1000步奖励2个积分,在之后每2000步奖励3个积分,请同学们根据规则,画出获得积分的流程图。
①输入步数t
②判断步数t是否小于等于4000步,
如果是执行③,如果不是执行④
③d=t/1000*2
④d=4000/1000*2+(t-4000)/2000*3
⑤输出积分d
d=t/1000*2
d=8+(t-4000)/2000*3
输出d
结束
开始
输入t
t<=4000
Y
N
算法描述
实践3:李明同学为了在下次的远足中争当领旗手,计划在远足前一周恢复体能,第一天走2500步,之后每一天都比前一天多走1200步,请同学们设计算法看看小明第7天需要走多少步?
①日期x=1,步数t=2500
②x=x+1,t=t+1200
③判断x是否小于7,
如果是继续执行②,如果不是执行④
④输出t的值
开始
x=1,t=2500
x=x+1,t=t+1200
x<7
输出t
结束
Y
N
算法基本结构
开始
x=1,t=2500
x=x+1,t=t+1200
x<7
输出t
结束
Y
N
开始
输入t
d=t/1000*2
输出d
结束
顺序结构
选择结构
循环结构
d=t/1000*2
d=8+(t-4000)/2000*3
输出d
结束
开始
输入t
t<=4000
Y
N
练习评价
请同学们打开文件接收柜的“课堂检测”,完成练习并对自己进行评价。
算法总结
课后拓展
课本P51
欧几里得算法——辗转相除法
设给定的两个正整数为m和n,求他们的最大公约数
任选一种描述方法(自然语言、伪代码、流程图)表示出来
3 . 2 算 法 及 其 描 述
初识算法
为了庆祝建党一百周年,高级中学举办了“百年逐梦路,青春励志行”研学旅行活动。相信同学们参加后受到了很大的鼓舞,从深层次的感悟到了红色历史、红色文化,也加深了与同学们之间的友谊。我们兄弟学校的李明同学也迫不及待的想要组织一次远足活动,请同学们根据地图上标识的打卡地点,在每个打卡地点中安排一到两个休息点,帮助李明同学设计一条的远足路线。
初识算法
打卡地点 ①高级中学②城市会展中心 ③119消防文化主题公园
可以选择的休息点:福莱山文化公园、永旺梦乐城、37度梦幻海水乐园、海纳科技文化广场、天地广场、烟台金沙滩海滨公园。
算法定义
算法,就是在有限步骤内,求解某一问题所使用的一组定义明确的规则。
示例:判断6x +9x+7=0是否有实数根。
①计算d=9*9-4*6*7
②判断d是否大于等于0,如果是执行步骤③,否则执行步骤④
③输出此方程有实数根
④输出此方程无实数根
算法定义
任务1 设计算法:输入a、b两个数的值,输出时交换两个数的值。
①输入a和b
②另取一个值c,把a的值赋给c
③将b的值赋给a
④将c的值赋给b
⑤输出a,b
算法特征
分析算法 判断6x +9x+7=0是否有实数根 输入a、b两个数的值,输出时交换两个数的值
是否有输入?
是否有输出?
执行的步骤个数是多少?
每一步是否有确切的含义?
是否能在有限的时间完成?
任务2 根据示例和任务1的算法,填写以下分析算法的表格
算法特征
算
法
的
特
征
数据输入
一个算法必须有零个或多个数据输入。
数据输出
一个算法有一个或多个数据输出。
有穷性
算法必须在有限的步骤内停止。
确定性
算法执行的每一个步骤必须有确定的定义。
可行性
算法的每个计算步骤都是可以执行的。
算法描述
实践1:李明同学想用一款软件测量他们走了多远,他平时运动时喜欢用爱动APP去测量步数,可以奖励积分,积分可以用来兑换名著。该APP规定,每走1000步就奖励2个积分,请同学们设计算法,实现输入相应的步数t就能看到有多少积分d。
算法描述
1、自然语言:人们日常所用的语言。
易于理解
引起歧义
①输入步数t
②计算积分d=t/1000*2
③输出积分d
他原来在这里
(1)以前
(2)表示某种真实的情况
算法描述
2、伪代码:介于自然语言和计算机语言之间的文字和符号。
格式紧凑、书写方便、便于向计算机程序设计语言过渡
不适用于没有代码基础的初学者
Input t
d=t/1000*2
Print d
算法描述
3、流程图:步骤简洁清晰、算法结构表达明确、直观易读。
图形 名称 功能
开始/结束 表示算法的开始或结束
输入/输出 表示算法中变量的输入或输出
处理 表示算法中变量的计算与赋值
判断 表示算法中的条件判断
流程线 表示算法中的流向
连接点 表示算法中的转接
算法描述
①输入步数t
②计算积分d=t/1000*2
③输出积分d
开始
输入t
d=t/1000*2
输出d
结束
请同学们对应着自然语言,自主学习流程图图形(课本P50),将此流程图补充完整。
开始
输入t
d=t/1000*2
输出d
结束
算法描述
实践2:后期爱动APP对奖励规则进行了更新,每天走路的前4000步,每1000步奖励2个积分,在之后每2000步奖励3个积分,请同学们根据规则,画出获得积分的流程图。
①输入步数t
②判断步数t是否小于等于4000步,
如果是执行③,如果不是执行④
③d=t/1000*2
④d=4000/1000*2+(t-4000)/2000*3
⑤输出积分d
d=t/1000*2
d=8+(t-4000)/2000*3
输出d
结束
开始
输入t
t<=4000
Y
N
算法描述
实践3:李明同学为了在下次的远足中争当领旗手,计划在远足前一周恢复体能,第一天走2500步,之后每一天都比前一天多走1200步,请同学们设计算法看看小明第7天需要走多少步?
①日期x=1,步数t=2500
②x=x+1,t=t+1200
③判断x是否小于7,
如果是继续执行②,如果不是执行④
④输出t的值
开始
x=1,t=2500
x=x+1,t=t+1200
x<7
输出t
结束
Y
N
算法基本结构
开始
x=1,t=2500
x=x+1,t=t+1200
x<7
输出t
结束
Y
N
开始
输入t
d=t/1000*2
输出d
结束
顺序结构
选择结构
循环结构
d=t/1000*2
d=8+(t-4000)/2000*3
输出d
结束
开始
输入t
t<=4000
Y
N
练习评价
请同学们打开文件接收柜的“课堂检测”,完成练习并对自己进行评价。
算法总结
课后拓展
课本P51
欧几里得算法——辗转相除法
设给定的两个正整数为m和n,求他们的最大公约数
任选一种描述方法(自然语言、伪代码、流程图)表示出来
同课章节目录
- 第一章 数据与信息
- 项目范例 体验庆祝国庆多媒体作品的数据与信息处理
- 1.1 数据及其特征
- 1.2 数据编码
- 1.3 信息及其特征
- 第二章 知识与数字化学习
- 项目范例 运用数字化工具探究数理知识
- 2.1 知识与智慧
- 2.2 数字化学习与创新
- 第三章 算法基础
- 项目范例 设计从A市到B市耗时最少的旅行路线方案
- 3.1 体验计算机解决问题的过程
- 3.2 算法及其描述
- 3.3 计算机程序与程序设计语言
- 第四章 程序设计基础
- 项目范例 设计购买纪念品的最佳方案
- 4.1 程序设计语言的基础知识
- 4.2 运用顺序结构描述问题求解过程
- 4.3 运用选择结构描述问题求解过程
- 4.4 运用循环结构描述问题求解过程
- 第五章 数据处理和可视化表达
- 项目范例 网络购物平台客户行为数据分析和可视化表达
- 5.1 认识大数据
- 5.2 数据的采集
- 5.3 数据的分析
- 5.4 数据的可视化表达
- 第六章 人工智能及其应用
- 项目范例 剖析空调企业智能客服机器人
- 6.1 认识人工智能
- 6.2 人工智能的应用
